World Journal of Nuclear Science and Technology
Vol.06 No.03(2016), Article ID:69063,21 pages
10.4236/wjnst.2016.63019
Analytical and Computational Analysis of Flow Splitting in Multiple, Parallel Channels Systems
Alejandro I. Lazarte1, J. C. Ferreri2*
1Autoridad Regulatoria Nuclear, Buenos Aires, Argentina
2Academia Nacional de Ciencias de Buenos Aires, Buenos Aires, Argentina

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 April 2016; accepted 23 July 2016; published 26 July 2016
ABSTRACT
Previous analytical results on flow splitting are generalized to consider multiple boiling channels systems. The analysis is consistent with the approximations usually adopted in the use of systems codes (like RELAP5 and TRACE5, among others) commonly applied to perform safety analyses of nuclear power plants. The problem is related to multiple, identical, parallel boiling channels, connected through common plena. A theoretical model limited in scope explains this flow splitting without reversal. The unified analysis performed and the confirmatory computational results found are summarized in this paper. New maps showing the zones where this behavior is predicted are also shown considering again twin pipes. Multiple pipe systems have been found not easily amenable for analytical analysis when dealing with more than four parallel pipes. However, the particular splitting found (flow along N pipes dividing in one standalone pipe flow plus N − 1 identical pipe flows) has been verified up to fourteen pipes, involving calculations in systems with even and odd number of pipes using the RELAP5 systems thermal-hydraulics code.
Keywords:
Multiple Parallel Boiling Channels Systems, Asymmetric Splitting Flow, Verification of Codes, Systems Thermal-Hydraulics Codes, Nuclear Engineering

1. Introduction
In nuclear power plants reactors, natural circulation is one of the mechanisms for decay heat removal after a transient or accident. In this type of installations, multiple parallel tubes are a common system configuration. The complexity of the flow pattern may be exemplified by simply mentioning that after a very small break loss of coolant accident (SBLOCA), the natural circulation flow map shows different regimes, from single or two- phase natural circulation to reflux condensation regime (see e.g. [1] and [2] ). The main task is verifying whether those designs can avoid the development of instabilities in transients under nominal and postulated accident conditions or, also important from the point of view of nuclear safety evaluations, that system codes used for such safety evaluations are capable of capturing the instabilities threshold. There is plenty of consolidated literature on this subject and a review (see [3] ) confirms this assertion.
The behavior of a set of parallel tubes or inverted U-tubes under natural or forced circulation systems in single and two-phase flow with common inlet an outlet may become complex. It is well known that these configurations can develop several types of instabilities, classified as static or dynamic. In the first case, only steady- state conservation laws are required for instability prediction.
In a previous study (see [4] ), the present authors analyzed steady asymmetric flow splitting coming from static instabilities in thermodynamic conditions representative of a SBLOCA in an integral test facility (SEMISCALE) that have steam generators with two different pipes which, looking for results symmetry, were firstly considered identical with average height. This system configuration lead to non-symmetric flow splitting between the steam generator pipes. Because of this, twin channels systems had been considered in detail and the basic mechanism leading to the asymmetric flow splitting was elucidated; a map was constructed showing the conditions for such behavior and the approximate, theoretical results verified using the systems thermo-hydraulics code [5] .
Other authors have studied flow rate distribution (see [6] and [7] ) in very long evaporating parallel pipes and performed a stability analysis, and the corresponding experiments related to solar energy collecting pipes. More recently, related studies with three or four pipes systems have been presented by [8] showing flow instabilities leading to flow mal-distribution in the system, i.e. non-symmetrical flow splitting.
In this paper, previous results from the present authors are extended with a unified analysis to consider multiple but still small (up to fourteen) number of N identical boiling pipes systems. Results have been verified through RELAP5 calculations. The interest in increasing the number of channels came from the possible existence of instabilities during transients in nuclear reactor designs under analysis with flow driven by gravity coming in (twelve) virtual fluid channels from a core exit cross section. As a consequence, results have been obtained for thermodynamic conditions corresponding to nuclear reactor designs. When considering multiple pipes, the possible flow splitting became even more complicated and above four, and the behavior was only studied using RELAP5. The peculiarity of the results is that under certain conditions, the splitting consisted in an increased fraction of mass flow in one pipe and the corresponding remaining fraction distributed in equal mass flow rates in the remaining N − 1 pipes. No reverse flow exists. The conditions for such a behavior has been established and represented in maps numerically computed with an in-house developed code and verified, as mentioned before, using the systems thermal-hydraulics code RELAP5. Not surprisingly, modification of simulation options (such as user options on models or numerical schemes) with the systems codes may lead to different predictions, including code failure.
It may be of interest to introduce here a comment on the role of the scope of the analytical model: even when the hypothesis may look restrictive, for the intended application they are appropriate. This has been verified using a code with no approximations regarding friction losses and with two-fluid models. The agreement was very satisfactory providing confirmation of the appropriateness of the hypothesis made for this analysis. However, it should be noted that depending on boundary and geometrical consideration in the analytical models as presented in this work and in other references, flow recirculation in the inlet or outlet plenums may not be captured. This is due to model simplifications but these peculiarities may be captured with system code such as RELAP5. Again, it is pointed out that the results herein shown are directly applicable to nuclear reactors because of the working conditions considered. This is coherent with the previous results of the authors as shown in what follows.
2. Two Parallel Boiling Channels
To introduce the analysis and due to its simplicity, the results of [4] are briefly reconsidered here. A typical single boiling channel has a characteristic curve as shown in Figure 1. Depending on operating conditions, the classical sigmoidal curve has a local minimum and a maximum that typically separates liquid and vapor single phases, respectively. In between, there is a two-phase flow region. The shape of the curve strongly depends on the relative contribution of gravitational, acceleration, form and friction effects to pressure drop. Plenty of literature
Figure 1. Single boiling channel characteristic curve.
describes this curve and analyze the channel behavior depending on boundary conditions and may be found in [3] [9] and [10] . For a constant inlet pressure, there could be one or three possible mass flow rates.
Different approximations to analyze this problem are considered in what follows.
2.1. Lumped Parameter Model
Let us consider a single boiling pipe and homogeneous, equilibrium fluid model (HEM) as shown in Figure 2. Heat flux is uniform along the tube and three regions may be observed: liquid only, steam only and two-phase regions.
The pressure drop along such a boiling channel may be written as:
 (1)
(1)
where ZB is the non-boiling length, W is the mass flow rate, A is the channel flow area, g is the gravity acceleration, L is the channel length, f is the friction factor (assumed constant in this analysis and equal in single and two phase flow and denoted as fTP), ρf is the liquid density at saturation and ρm is a mean density in the two phase region. For simplicity, as the mean density, the outlet density was used. Parameters ki and ke are the concentrated friction values at the inlet and outlet of the individual channels, respectively. 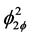 is the two-phase friction factor evaluated at outlet conditions, it is defined as,
is the two-phase friction factor evaluated at outlet conditions, it is defined as,
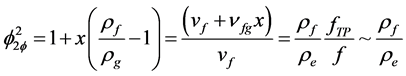 (2)
(2)
where ρe is the mixture density at the channel outlet.
Dry steam zone in the pipe is not considered for these stability studies because, as it will be shown latter, instabilities are expected to occur when fluid becomes saturated. The acceleration term may be disregarded for this analysis because it has low relevance on the instability threshold. In passing, it facilitates finding the analytical solution.
Some useful (and commonly used) definitions are:
 (3)
(3)
Figure 2. Single boiling channel.
where Np, NS and Nfr are the phase change, subcooling and friction dimensionless numbers; vfg is the difference between the gas and liquid specific volumes and hf and hfg are the saturation and latent heat, respectively.
In two parallel and identical channels the pressure drop through then are equal; i.e. ΔP1 = ΔP2. It is well known that this system may have several stable solutions. This means that for equal pressure drop, different mass flow rate for each tube come up.
In previous references, like in [11] the pressure drop along channels is assigned and kept constant as a boundary condition. However, in this case, the inlet mass flow rate and outlet pressure are fixed. From mass conservation: W1 + W2 = WT (constant).
Defining: 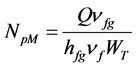 and
and 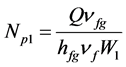 and setting f as the ratio of channel 1 mass flow rate to the total inlet mass flow rate,
and setting f as the ratio of channel 1 mass flow rate to the total inlet mass flow rate,

Then
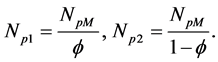
The dimensionless magnitude NpM is the phase change number corresponding to a channel with same imposed heat as the single channel but with the total system mass flow rate. The channel non-boiling length ZB1 and ZB2 are defined as the positions at which the fluid in each channel becomes saturated, that is
 . (4)
. (4)
Each pressure drop term will be evaluated in what follows. Recall that the expression of ΔP for channel 2 will be the same as for channel 1, exchanging f by (1 − f). The friction terms in (1), using the definition of the dimensionless numbers, reads
 (5)
(5)
where 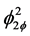 was replaced by
was replaced by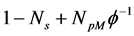 .
.
The gravity contribution, results,
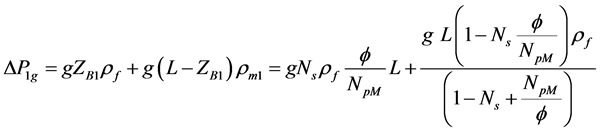 . (6)
. (6)
Once again, the value ρm1 will be calculated at the exit quality turning out ρe1. Adding (5) and (6), the total pressure drop along channel 1 is obtained, based on the hypothesis of the model.
The pressure drop ΔP2 comes from to ΔP1 changing f by 1 − f. Then


For simplicity, kem and kim denote ke and ki divided by Nfr. The objective is to find the fixed points of the equation

where Fo is the Froude number defined as

The velocity v is the inlet velocity and it was expressed as function of the total mass flow rate WT. The area corresponds to one channel flow area.
When gravity is added to the pressure drop term, the function 
2.2. Pressure Drop Characteristic Curve for Two Parallel Tubes
As shown in Figure 1, depending on the external characteristic, the system (a single boiling tube), may experiment different steady states. For instance, for a constant external pressure the system could have at most three mass flow rate, namely: Wi with i = 1 to 3. When two pipes are joined together, then up to nine steady states may arise combining all possible the mass flow rates.
Then, at most, 3N different mass flow rates may arise, with N the number of pipes. When identical pipes are used, several solutions are the same and are disregarded. For two identical pipes, at most 6 possible solutions may be obtained. Straightforward application of the lumped parameter model considering the values shown in Table 1, allows obtaining the inlet pressure curve (constant inlet mass flow rate and outlet pressure. The procedure was:
1) For each inlet pressure within a range, all possible mass flow rates are determined.
2) Since both channels have the same mass flow rate, then for each inlet pressure the total mass flow rate is determined as the sum of individual channels mass flow.
3) The inlet pressure is plotted for each mass flow as it is shown in Figure 3.
Figure 3 shows a typical “∞” shape. For large and small mass flow rate, the system behaves as one single channel working with a single-phase fluid (liquid or vapor). In between there is a complex region showing interaction and feedback between channels (between points A and B). Since, both pipes are identical then the numbers of mass flow possible states are less than 9; as it was stated above, for a constant inlet pressure (dotted line in the figure) there are 6 possible solutions. The shape of the curve depends on the characteristic curve of each channel, which in turn is a function of friction losses and power delivered to the fluid.
Recalling the fraction of flow splitting f1 = W1/WT, a flow splitting map as function of the total mass flow rate is depicted in Figure 4.
In Figure 4, it may be observed that as the mass flow rate decreases from 0.2 to 0.16 kg/s three possible states appear. Two of them correspond to symmetric flow splitting. The total flow rate at which flow splitting begins coincides with the position at which the derivative of the pressure drop curve changes the sign (at A and B).
Table 1. Numerical values used in the calculations, like in [2] .
Figure 3. Pressure drop characteristic curve for two parallel channels.
Figure 4. Flow splitting in twin parallel channels as a function of total mass flow rate. Results from lumped parameter model and parameters values from Table 1.
2.3. Stability Analysis of Two Parallel Boiling Channels
The momentum conservation equation for two channels may be written as


Being mk = Lk/Ak, WT and Wk are the total and the k (i.e. 1 or 2) channel mass flow rates, respectively. Recalling that W1 + W2 = WT, and m = m1 = m2 (from hereinafter all channels are assumed identical among them). Perturbing the mass flow rate in both channels and the total as Wk = Wk0 + δWk, where Wk0 corresponds to the steady state solution and δWk are the infinitesimal perturbations.
Now, considering that the perturbation may be written as δwk = βkeλt. Calling

Finally, the above system equations could be written in matrix form. The determinant of the system of equations is:

The characteristic equation is 

The system is stable to perturbations when the real part of the characteristic equation roots are negative, i.e.


For a constant mass flow rate or a vertical external characteristic curve,

It could easily verified that the system is stable if

or

Since ΔP1 y ΔP2 are functions of f (the mass flow rate fraction) then

For twin parallel boiling channels, using the lumped parameter model disregarding the gravity contribution the stability region could be easily obtained, given by

with the constrain that Npm ≥ Ns/f. For
that shows the stability map for a two twin boiling parallel channel with vanishing gravity force contribution; the inner area corresponds to the instability area. It has to be remarked that the horizontal axis is NpM variable defined as the phase change number of channel with total system flow rate and the power of individual channel, i.e. Np1 = 2NpM since f = 0.5. The red lines indicate the thermodynamic quality of one in a single channel.
As stated above, a stability map may be built using the analytical expression (22) for twin parallel channels. However, in what follows a larger number of channels will be considered, so an analytical expression may be complex to obtain. Another, but equivalent way for plotting the stability map for twin channels, is evaluating the pressure drop over the Ns − NpM plane for a constant total mass flow rate f = 0.5 ± Δ, for each channel. This corresponds to use (21). Here D is a small and arbitrary parameter used to calculate a finite difference around 0.5. The difference of pressure drop in each channel divided by 2D gives the plotted discrete approximation of the derivative.
Figure 6 shows the stability region with gravity contribution. It may be observed by comparison with Figure 5 that gravity tends to stabilize the system for a constant subcooling number. This is consistent with the results obtained by Popov et al. in [12] , indicating that the critical subcooling number (minimum subcooling number) increases when gravity is included. On the other hand, it should be remarked that absence of gravity is conceptually different from considering a horizontal channel, since pressure drop in the two-phase region should also take into account the pipe flow pattern.
Figure 5. Stability map obtained by lumped parameter model for twin boiling parallel pipes. No gravity contribution. Parameter values from Table 1.
Figure 6. Stability map obtained by lumped parameter model for two twin boiling parallel pipes considering gravity contribution and using values from Table 1.
2.4. Parametric Studies
It is usual to perform parametric studies to check the effects of different system parameters on its overall behavior. For instance, in Figure 5 and Figure 6 the effect of gravity in the stability curve was clearly shown. Keeping all parameters constant and switching on gravity contribution the unstable region becomes greater and the minimum value (vertex) moves to lower Ns values. The outlet concentrated pressure losses tend to destabilize the system, so increasing the outlet concentrated pressure coefficient ke to 10 or 50 as is shown respectively in Figure 7 and Figure 8, the instability regions are enlarged and the minimum subcooling number moved to lower values, equivalent to higher inlet temperatures.
In Figure 9, instead of a flow splitting, a RELAP5 simulation shows mass flow rate out-of-phase oscillation.
Figure 7. Stability map obtained by lumped parameter model for two twin boiling parallel pipes, considering gravity contribution and using values from Table 1 with the exception of ke = 10.
Figure 8. Stability map obtained with lumped parameter model for twin boiling parallel pipes, considering gravity contribution and using values from Table 1 but ke = 50.
Figure 9. Calculated RELAP5 mass flow rate for twin boiling parallel pipes with the same conditions of Figure 8.
This oscillation shows a sign change indicating intermittent flow reversal. Static instabilities and dynamic instabilities in boiling channel may come up together, and both could be distinguished due to the oscillation characteristic time. For instance, density wave instabilities have larger oscillatory frequency in relation to pressure drop oscillation. Another example of this behavior will be shown later.
3. Multiple (>2) Parallel Boiling Channels
The procedure performed in [6] is partially rewritten here for understating and will be followed in the rest of the section.
In this section a general procedure to get the stability regions for multiple identical boiling pipes is outlined. A stability map is built, as above, evaluating the stability condition related with pressure drop over the Ns − NpM plane for a constant total mass flow rate.
For an arbitrary number of parallel boiling channels, the procedure becomes somewhat cumbersome. Writing the momentum conservation equation for each channel, perturbing their flow rates with respect to the steady state values and rearranging, N differential equations are obtained. Writing the set of equation in matrix form:
where mk is quotient between length and channel area, 
mass flow rate. Stability regions are determined by finding the conditions where the real part of the characteristic equation roots is negative. Analytical conditions could be written based on the coefficient of the characteristics equations but are difficult to apply. From Hurwitz theorem, it could be derived that a necessary condition for having negative real roots is that all characteristics coefficients should be negative. However, the reverse is not true.
The conditions for flow stability for N parallel identical channels then become


Recalling that the fraction of mass flow though a channel is:

when bifurcation or the conditions for several multiple steady states are met in N parallel channels, the splitting will develop in pairs. The latter means that N − 1 channel will have the same flow rate and only one different. The flow ratio for N − 1 is equal, and hence

and the fraction of the individual channel as function of the other N − 1 channel results:

Since

Considering that

The latter expression is the necessary condition for N parallel tubes with the condition that splitting is channel to channel. The quantity 


3.1. Application to Three Parallel Boiling Channels
For three parallel channels, we follow the same procedure as in Section 2.3, namely: writing the momentum conservation equation for each channel, perturbing their flow rates with respect to the steady state values and rearranging, the system characteristic equation is determined from the vanishing determinant of the following matrix.

It was assumed, as above, that the three channels have the same length and flow area and its ratio is denoted by m. The characteristic equation has the form:
To determine the stability regions, the conditions to get a negative real part of the characteristic equation roots must be found. Applying the Hurwitz theorem said conditions are:



Recalling that



The third condition could be analyzed in the following way. Replacing 

Condition (35), neglecting the first term in brackets, may be rewritten
or

The above expression is a necessary condition to get the stability region for static instabilities for three boiling parallel channels. It must be noted that stability depends on a single channel stability condition since if just one of the 
3.2. Application to Four Parallel Boiling Channels
The stability conditions for four channels are:

It may be shown using a similar procedure performed previously for three channels that the necessary conditions are:

and

Both Equations (31) and (32) are necessary conditions for stability.
4. Multiple Channel Stability Maps
Stability maps for any number of channels may be constructed by using expression (23) and (28). In the latter equations no assumptions should be made, however; more computational time is required if the same number of points have to be evaluated. For the sake of simplicity, only cases with HEM model and gravity are shown in this section and the same conclusions could be applied for HEM neglecting gravity or considering the two fluid model. Figure 10 shows the stability map for two to five identical parallel channels. The map is plotted as function of the NpM to consider any number of channels in the same graph. When the number of channels is increasing, the left boundary of the instability region increases its slope and the area becomes smaller while keeping constant the concentrated pressure drop coefficients at the inlet and outlet. It may be observed that unstable regions overlap for all the configurations shown. Further refinement of the sample grid to eliminate the ripple was not attempted.
5. RELAP5 Calculations
RELAP5 is a best estimate systems thermal-hydraulic code extensively used for nuclear safety evaluations related to nuclear power plants. It provides numerical results using closure correlations and steam tables. Results heavily depend on user choices. The present authors discussed in detail the effects of different code options and fluid models (see [4] and also [11] ). It is important to state here, consistently with the introduction, that the predictions using this thermo-hydraulic system code confirmed the approximate model predictions.
Figure 11 shows a sketch of the geometry implemented for a four identical pipes system. The pipes were divided into 48 cells. The inlet mass flow rate is imposed with a time dependent junction, the outlet pressure is fixed with a time dependent volume. Simulations have been performed using both HEM and the two fluid models.
It is interesting to verify firstly the behavior of a system composed of three or four parallel channels. For simulating this case, additional pipes have been added in parallel to the twin pipes case and identical to the others. The inlet mass flow rate and power delivered to the channel were changed accordingly. It must be noted that the same rate of power delivered to the fluid was not used in all cases. The system behavior for three parallel channels using RELAP5 with and without gravity and the HEM or two-phase flow model is shown in Figure 12. Considering vanishing gravity there is a flow splitting at 1300 s, corresponding in this case to 125 kW. The flow splitting is asymmetrical; that is, one pipe increases its flow rate while the other channels reduce proportionally their flow rate and is equal among them. This behavior supports the hypothesis used for deriving the instability area in three pipes systems.
When gravity is taken into account using HEM, no flow splitting was observed at least at the expected power. Moreover, the RELAP5 code fails near to the 2000 s, corresponding to 200 kW. On the contrary, with two-fluid model and gravity, flow splitting occurs at 1300 s, corresponding to 167 kW.
Figure 10. Stability map for 2, 3, 4 and 5 identical parallel channels.
Figure 11. RELAP5 nodalization for a system with four identical pipes.
Figure 12. RELAP5 calculated mass flow rate along three channels (named 1, 2 and 3). There is a stable flow splitting for the HEM with vanishing gravity contribution and with the two-fluid model. No splitting exists for HEM model with gravity contribution.
RELAP5 calculations for four identical channels considering different modeling options are shown in Figure 13, Figure 14 and Figure 15. When gravity is taken into account, no flow splitting took place unless exit k’s values are increased as the case in Figure 13 and Figure 14, respectively. Flow splitting for vanishing gravity or with gravity and ke equal to 25 comes at 119 kW, whereas for two fluid model near to 170 kW. This is consistent with the three channel models showing that two fluid model requires more power to become unstable. This difference might be due to the nucleate subcooled boiling region before fluid saturation. In all cases ki was set to 23.
In addition, as in the three channels case, flow splitting appears in (1 and N − 1) pairs. It should be noted that power required for flow splitting is almost independent of the number of channels; this means that for two, three or four parallel channels the needed power is ranged between 120 to 130 kW. This supports the idea that flow splitting or flow mal-distribution in the system comes up when a single tube becomes unstable.
It is interesting to consider a 3D representation of the flow splitting for the four tubes case plotting the time variation of NpM for a given value of Ns when power is increased (then changing the value of flow rate). This plot is shown in Figure 16. Starting at 2000 s the power is kept constant and set as 120 kW to avoid code failure. This explains the change in the slope observed. At t = 0 s, the plane Ns vs NpM shows the instability zone as predicted by the theoretical analysis. The case shown corresponds with Figure 14. As may be observed, the variation of NpM for Ns =15 shows that splitting occurs when NpM reaches the left limit of the instability zone as predicted by the theoretical analysis.
Figure 13. RELAP5 calculated mass flow rate for a four parallel pipe arrangement with HEM model and vanishing gravity. There is a stable flow splitting.
Figure 14. RELAP5 calculated mass flow rate for a four parallel pipe arrangement with HEM model and gravity contribution. The exit concentrated pressure losses coefficient was set to 25. Stable flow splitting is observed.
Figure 15. RELAP5 calculated mass flow rate for a four parallel pipe arrangement with two fluid model and gravity contribution. The exit concentrated pressure losses coefficient was set to 5. Stable flow splitting is observed.
Figure 16. RELAP5 calculated NpM for Ns = 15 in a four parallel pipe arrangement with HEM model and gravity contribution. Representation corresponds to Figure 14. Stable flow splitting is observed.
Some results for nine and twelve parallel identical tubes using a two fluid model are shown in Figure 17 and Figure 18, respectively.
For nine parallel identical tubes, flow splitting comes again in pairs supporting the previous results for two, three and four identical channels. As above, eight channels increases their mass flow rates while the one decreases it. It is interesting to note that the channel that increases the mass flow rate after flow splitting becomes subcooled. When running the above cases with the HEM model, the fluid in the individual channel is in single phase while in the two fluid model remains in subcooled boiling with a fluid temperature closed and below to saturation. This implies that the other eight channels work in nucleate boiling with a very high flow quality.
Flow oscillations may be observed in Figure 18 after flow splitting for twelve tubes by increasing power delivered to the fluid. This oscillation corresponds to a dynamic instability of density wave type. It must be noted that flow splitting comes, once again, in pairs (1 tube increase or decrease flow rate while the other eleven increase their flow rate proportionally).
Figure 17. RELAP5 calculated mass flow rate for nine parallel pipes with two fluid model. Stable flow splitting is observed; eight channels increase mass flow and the other decreases mass flow.
Figure 18. RELAP5 calculated mass flow rate for twelve parallel pipes with two fluid model. Stable flow splitting is observed before density waves appear. Eleven channels increase mass flow and the other decrease mass flow.
Despite of the behavior showed in Figure 18, as the numbers of channels are increased results become strongly dependent on user options as well as on the boundary conditions configuration. In Figure 19, the mass flow rate for a case with 14 identical parallel channels is shown using the two fluid model and all conditions as in Table 1 except that the value for ke, set to 10. In this fourteen channels configuration, two channels increase the mass flow rate while the rest decrease it. This unexpected (2 & N − 2) result may imply that analytical stability prediction is just a necessary but not sufficient condition for the 1 & (N − 1) splitting or that other effects may come up with increasing number of channels.
The flow splitting should be related to static instabilities since one channel increases mass flow rate with the other channels decrease. Figure 3 may be used for the explanation: when system conditions are approaching to point A in the figure, the system will experiment flow splitting, since that point behaves as a rejection point pushing one of the mass flow rates back to right. From mass conservation, the other jump to the two-phase region. This explanation suits well for systems with a small number of identical channels. Small differences may preclude this behavior.
Figure 19. Calculated mass flow rate for fourteen identical parallel pipes with two-fluid model. Stable flow splitting is observed. Twelve channels increase mass flow and two decrease mass flow.
6. Conclusions
Static instabilities in boiling channels with common plena, fixed inlet mass flow rate and outlet pressure have been studied. An analytical simplified model using HEM was first developed to study static instabilities in twin parallel channels. The latter analysis was extended to three and four parallel channels and, finally, for N parallel channels. Using a perturbation analysis to the momentum equation for HEM model, a stability analysis was performed for two, three and four parallel channels and a necessary condition and the stability maps based on dimensionless numbers were obtained. It was shown that when the instability boundary was crossed, the mass flow rate in the channels split in non-symmetric ways. When a larger number of channels are considered, it is found (using RELAP5 systems thermal-hydraulics code) that splitting also comes up in this particular way: one channel increases (decreases) mass flow whereas the other N − 1 channels decrease (increase) mass flow rates. From necessary stability conditions, a system with several parallel channels may be stable while some of the channels fall individually in the unstable condition.
Concluding, stability maps for flow splitting in a system of up to fourteen identical parallel pipes have been considered, showing similar behavior although the splitting occurs first in the expected way followed by another one. This stands for the latter case in the explored range of parameters. It is shown that gravity has a stabilization effect in the sense that the unstable region becomes smaller. In addition, when the outlet concentrated pressure drop coefficient increases, the system becomes more unstable, as is well known from density wave oscillations analysis. Both instabilities may appear in sequence.
Cite this paper
Alejandro I. Lazarte,J. C. Ferreri, (2016) Analytical and Computational Analysis of Flow Splitting in Multiple, Parallel Channels Systems. World Journal of Nuclear Science and Technology,06,170-190. doi: 10.4236/wjnst.2016.63019
References
- 1. D’Auria, F. and Frogheri, M. (2002) Use of Natural Circulation Map for Assessing PWR performance, Nuclear Engineering and Design (Special Issue), 215, 111-126.
http://dx.doi.org/10.1016/S0029-5493(02)00045-6 - 2. Lazarte, A.I. and Ferreri, J.C. (2012) Natural Circulation Characterization of the CNA-II PHWR based on Flow Maps using RELAP5. 9th International Topical Meeting on Nuclear Thermal-Hydraulics, Operation and Safety (NUTHOS-9), Kaohsiung, Taiwan, 9-13 September 2012, Paper No. 9P0037.
- 3. Ruspini, L.C., Marcel, C.P. and Clausse, A. (2014) Two-Phase Flow Instabilities: A Review. International Journal of Heat and Mass Transfer, 71, 521-548.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2013.12.047 - 4. Lazarte, A.I. and Ferreri J.C. (2014) A Verification Problem for Thermal Hydraulics Systems Codes Dealing with Twin, Parallel-Boiling and Inverted U-Tubes Condensing Channels. Annals of Nuclear Energy, 68, 163-171.
http://dx.doi.org/10.1016/j.anucene.2014.01.016 - 5. USNRC (United States Nuclear Regulatory Commission) (2002) RELAP5/MOD3.3 Code Manual. Vol. 1-8, Information Services Laboratory Inc., Nuclear Safety Analysis Division, NUREG/CR-5535/Rev. 1.
- 6. Minzer, U., Barnea, D. and Taitel, Y. (2006) Flow Rate Distribution in Evaporating Parallel Pipes—Modeling and Experimental. Chemical Engineering Science, 61, 7249-7259.
http://dx.doi.org/10.1016/j.ces.2006.08.026 - 7. Baikin, M., Taitel Y. and Barneta, D. (2011) Flow Rate Distribution in Parallel Heated Pipes. International Journal of Heat and Mass Transfer, 54, 4448-4457.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2011.04.034 - 8. Zhou, J., Wang, S., Gao L., Zhao, L. and Pang, L. (2015) Study on Flow Instability inside Multiple Parallel Pipes of Direct Steam Generation. Energy Procedia, 69, 259-268.
http://dx.doi.org/10.1016/j.egypro.2015.03.030 - 9. Kakac, S. and Bon, B. (2008) A Review of Two-Phase Flow Dynamic Instabilities in Tube Boiling Systems. International Journal of Heat and Mass Transfer, 51, 399-433.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.09.026 - 10. Kakac, S. and Veziroglu, T.N. (1983) A Review of Two-Phase Flow Instabilities. In: Kakac, S. and Ishii, M., Eds., Advances in Two-phase Flow and Heat Transfer, Fundamentals and Applications, Vol. II, Springer, Netherlands, 577-667.
http://dx.doi.org/10.1007/978-94-009-6848-6_6 - 11. Ambrosini, A. and Ferreri, J.C. (2006) Analysis of Basic Phenomena in Boiling Channel Instabilities with Different Flow Models and Numerical Schemes. Proceedings of the 14th International Conference on Nuclear Engineering (ICONE 14), Miami, Florida, USA, 17-20 July 2006, 889-900.
http://dx.doi.org/10.1115/icone14-89863 - 12. Popov, N.K., Rohatgi, U.S., Rummens, H.E.C. and Duffey, R.B. (2000) Two-Phase Flow Stability in Low Pressure Parallel Vertical Heated Annuli. Proceedings of ASME/JSME/SFEN International Conference on Nuclear Engineering (ICONE 8), Baltimore, Maryland, USA, 2-6 April 2000, Paper #8568.
- 13. Akagawa, K., Sakaguchi, T., Kono, K. and Nishimura, M. (1971) Study on Distribution of Flow Rates and Flow Stabilities in Parallel Long Evaporators. Bulletin of JSME, 14, 837-848.
http://dx.doi.org/10.1299/jsme1958.14.837
Nomenclature
NOTES
*Corresponding author.





























