World Journal of Nuclear Science and Technology
Vol.2 No.1(2012), Article ID:16559,7 pages DOI:10.4236/wjnst.2012.21007
Application of Bootstrap in Dose Apportionment of Nuclear Plants via Uncertainty Modeling of the Effluent Released from Plants
Health Physics Division, Bhabha Atomic Research Centre, Mumbai, India
Email: ddatta@barc.gov.in
Received May 20, 2011; revised July 2, 2011; accepted August 25, 2011
Keywords: Dose Apportionment; Radioactive; Effluent; Cumulative Distribution; Bootstrap; Percentile
ABSTRACT
Nuclear power plants are always operated under the guidelines stipulated by the regulatory body. These guidelines basically contain the technical specifications of the specific power plant and provide the knowledge of the discharge limit of the radioactive effluent into the environment through atmospheric and aquatic route. However, operational constraints sometimes may violate the technical specification due to which there may be a failure to satisfy the stipulated dose apportioned to that plant. In a site having multi facilities sum total of the dose apportioned to all the facilities should be constrained to 1 mSv/year to the members of the public. Dose apportionment scheme basically stipulates the limit of the gaseous and liquid effluent released into the environment. Existing methodology of dose apportionment is subjective in nature that may result the discharge limit of the effluent in atmospheric and aquatic route in an adhoc manner. Appropriate scientific basis for dose apportionment is always preferable rather than judicial basis from the point of harmonization of establishing the dose apportionment. This paper presents an attempt of establishing the discharge limit of the gaseous and liquid effluent first on the basis of the existing value of the release of the same. Existing release data for a few years (for example 10 years) for any nuclear power station have taken into consideration. Bootstrap, a resampling technique, has been adopted on the existing release data sets to generate the corresponding population distribution of the effluent release. Cumulative distribution of the population distribution obtained is constructed and using this cumulative distribution, 95th percentile (upper bound) of the discharge limit of the radioactive effluents is computed. Dose apportioned for a facility is evaluated using this estimated upper bound of the release limit. Paper describes the detail of the bootstrap method in evaluating the release limit and also presents the comparative study of the dose apportionment using this new method and the existing adhoc method.
1. Introduction
During the normal operation of any nuclear facility gaseous and liquid radioactive effluents are routinely discharged into the environment. These can result in radiation dose to the members of the public through various exposure pathways. Regulatory authority (for example, Atomic Energy Regulatory Board in India) in line with the International Commission of Radiological Protection (ICRP), has prescribed an effective dose limit of 1 mSv/y for a member of the public which requires routine radioactive release to be authorized or stipulated within a limit. The objective of dose apportionment of the nuclear facilities including power plants, fuel reprocessing plant and waste immobilization plant is to establish the discharge limit of the gaseous and the liquid radioactive effluents into the environment so that the dose received by the members of the public will be 1 mSv/year. In India, the operating Nuclear Power Plants (NPPs) are situated at various parts of the country at Tarapur, Rawatbhata, Kalpakkam, Narora, Kakrapar, and Kaiga. At some sites, there are multiple units of NPPs as well as like Tarapur and Kalpakkam, other nuclear facilities like such as fuel reprocessing plant and waste immobilisation plant are also located. Thus, at the multi-facility sites it has to be ensured that the dose to public resulting from releases (atmospheric and aquatic route) from all the facilities does not exceed 1 mSv/y. Thus, the dose received by the members of the public is basically an integral quantity in the sense that, if there exists more than one facility then the sum total of the dose apportioned to each individual should be equal to 1 mSv/year. It is also envisaged that the risk to health resulting from the discharge of radionuclides into the environment will be influenced by factors that affect the magnitude of dose the individual receives. Computation of the release limit of these radioactive effluents is an issue of ensuring safety of the facility as well as safety of the environment. The existing discharge limits for the NPPs were established when the nuclear power program was at its initial stages. However, expansion program of nuclear power in the country demands the dose apportionment to be revisited in an appropriate scientific manner, so that release limits for the existing plants can be revised and the same for new plants to be installed at the same site can be established with the similar vintage. Statistical analysis of the existing discharge (gaseous and liquid effluents) data from the facility is taken into account to establish the release limit of that facility. Statistical analysis is carried out using bootstrap technique because of the imprecise structure of the release data. This paper presents the detail of bootstrap methodology [1] of arriving at the radioactive effluent release limits of Indian Nuclear Power Plants (NPPs). Bootstrap method of estimation of the discharge limits of the gaseous and liquid effluents also provides the knowledge of the cumulative distribution of the discharge. Cumulative distribution of the gaseous and liquid effluent discharge is used to estimate the uncertainty of the same and the uncertainty is expressed in the form of 5th and 95th percentiles. Uncertainty estimate of the discharges can be used in a standard dose assessment model to compute the uncertainty of the apportioned dose to a specific facility. Recommendation of dose apportionment can be finally be made with its 95th percentile value. Computation has been carried out using a computer code developed in house using Visual Basic 6.0.
2. Regulatory Control of Radioactive Discharge
Establishment of dose apportionment of a nuclear installlation is one of the important safety aspects in the sense that the task of dose apportionment will automatically provide the setting the limit of the discharge of the effluent both in the atmospheric and aquatic route. On the other hand, it will also provide the knowledge of how many more nuclear facilities can be possible to install at the same site. Dose apportionment scheme should follow the basic criteria as: the sum total of “dose apportionment of new facility”, “dose apportionment of old facility” and “the reserve” should be altogether equal to 1 mSv. In order to achieve this one has to set the appropriate limit of the discharge of the radioactivity into the atmospheric and aquatic environment. Recent work on the development of standards for the radioactive discharge control includes the development of practical guidance for setting discharge limits. ICRP Publication 60 [2] recommends justifying necessary measures for protection of the public in practice situations via constrained optimization procedures [3]. Public annual effective dose limit from all controllable environmental radiation sources (except of natural background) was already established as equal to 1 mSv. Accordingly, the constraint value relevant to a single source should be a nonspecified fraction of this limit. Both the dose limit and constraint apply to representatives of the highest exposed members of the public (the critical group) in the radiation conditions under consideration. According to the relevant Safety Fundamentals [4], “The objective of radioactive waste management is to deal with radioactive waste in a manner that protects human health and the environment now and in the future without imposing undue burdens on future generations.”
3. Bootstrap Method
Bootstrap procedures are robust nonparametric statistical methods that can be used to construct approximate confidence limits for the population mean, to estimate the bias and variance of an estimator or calibrate hypothesis tests [5]. In these procedures, repeated samples of size n are drawn with replacement from a given set of observations. The process is repeated a large number of times (e.g., thousands), and each time an estimate of the desired unknown parameter (e.g., the sample mean) is computed. Details of bootstrap and the diversity of its recent applications can be found elsewhere [5-9]. Bootstrap procedures assume only that the sample data are representative of the underlying population. The bootstrap procedures require no assumptions regarding the statistical distribution (e.g., normal, lognormal, gamma) of the underlying population and can be applied to a variety of situations [10]. However, since they involve extensive resampling of the data and, thus, exploit more of the information in a sample, that sample must be a statistically accurate characterization of the underlying population in all respects (not just in its mean and standard deviation). Therefore, the bootstrap methods are specifically useful when: the exact population distributions of the statistics are not known; or the critical values of the test statistics are not available; Bootstrap procedures are classified as (a) standard bootstrap, (b) bootstrap-t, (c) bias corrected accelerated (BCA) bootstrap and (d) percentile bootstrap [10]. In practice, it is random sampling that satisfies the representativeness assumption. Therefore the data must represent random samples of the underlying population. If sample size is small and the distribution is not known exactly bootstrap application on that sample generates the corresponding population and the population can be used to compute the upper confidence limit (UCL) of the population distribution. Bootstrapping procedures are inappropriate for use with data that were idiosyncratically collected or focused especially on contamination hot spots. Algorithm of bootstrap used for computing upper confidence limit (UCL) [11] is written below:
Algorithm:
Let X1, X2, ∙∙∙, Xn represent the n randomly sampled concentrations.
Step1: Compute the sample mean: 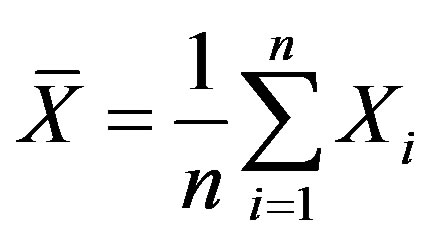
Step 2: Compute the sample standard deviation:

Step 3: Compute the sample skewness:

Step 4: For b = 1 to B (a very large number) do the following:
1) Generate a bootstrap sample data set; i.e.for i = 1 to n let j be a random integer between 1 and n and add observation Xj to the bootstrap sample data set.
2) Compute the arithmetic mean 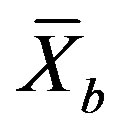 of the data set constructed in step 1.
of the data set constructed in step 1.
3) Compute the associated standard deviation sb of the constructed data set.
4) Compute the skewness kb of the constructed data using the formula in step 3.
5) Compute the studentized mean

6) Compute Hall’s statistic:

Step 5: Sort all the Q values computed in Step 4 and select the lower αth quantile of these B values. It is the (αB)th value in an ascending list of Q’s. This value is from the left tail of the distribution.
Step 6: Compute
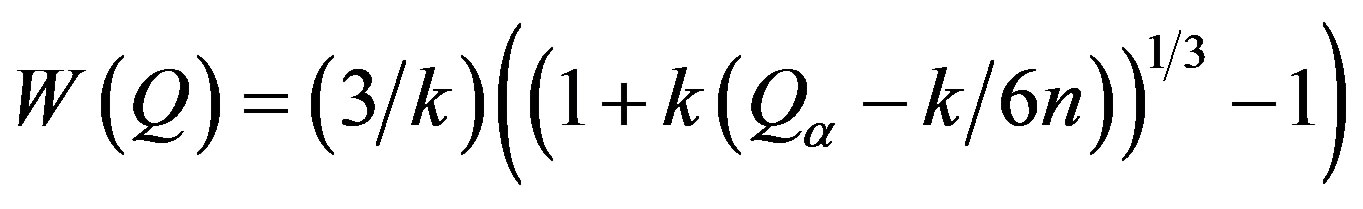
Step 7: Compute the one-sided (1-α) confidence limit on the mean.
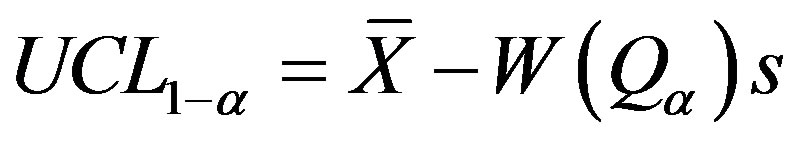
4. Mathematical Background of Dose Apportionment
4.1. Atmospheric Discharges
The dose apportionment methodology is basically a scheme to compute the dose to the member of the public at exclusion distance (1.6 km from location of the plant) corresponding to the discharge limit of the radioactive gaseous and liquid effluent released due to routine operation of the facility. This estimated dose should be a fraction of the limit 1 mSv/yr as stipulated by the regulatory authority. Discharge limit is considered as the technical specification limit of the discharge. Operational experience reveals that the actual discharge is always far below the technical specification as set up during the design of the plant. With a view to this fact, it is obvious that if we properly assess the discharge limit based on the operating experience of the facility, we can have the corresponding apportioned dose in a better perspective in the sense that we can have a substantial margin to reach at 1 mSv/yr limit resulting the provision of installation of some more new nuclear power plants or other nuclear facilities. Standard environmental dose assessment model along with the site-specific meteorological data and dietary intake data are used for the computation of dose. The dose to the members of the public can be mathematically formulated as
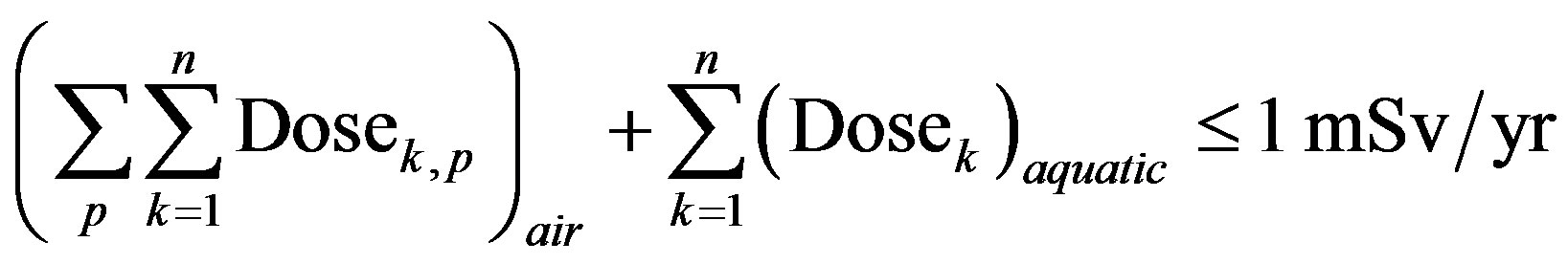 (1)
(1)
where, the index “p” denotes the pathways of exposure and the index “k” denote the radionuclide. Figure 1 gives the block diagram for the main steps in arriving at technical specification limits and dose apportionment. The dose received by the members of public is computed for all relevant pathways of exposure. The dose apportionment of fission product noble gas (FPNG) and Ar-41 is based on the dose versus release relationship and the Technical Specification limits for discharge. Mathematically the apportioned dose to FPNG and Ar-41 nuclide can be formulated as
 (2)
(2)
where, h is Tech spec limit and the other symbols have usual significance. The computation of plume doses in 22.5˚ sector from continuous release of noble gases (Ar-41 and fission product noble gases) can be found elsewhere in [12]. The sector receiving the highest dose is called as the
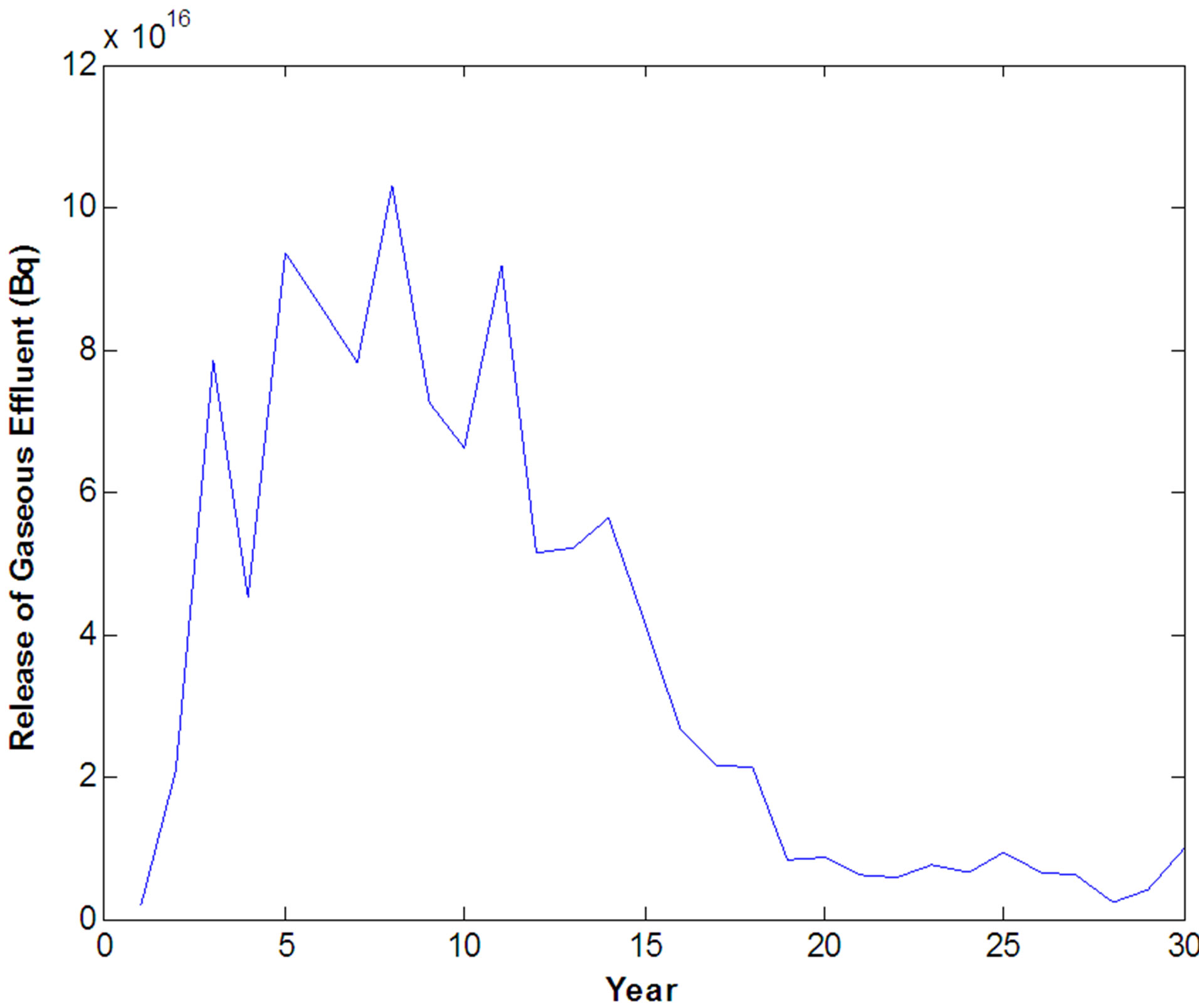
Figure 1. Distribution of yearly release of gaseous effluent from plant #1.
critical sector and subsequently sector average dose is used for computation for dose apportionment [12]. Accordingly, contributions from the adjacent two side sectors, on either side of main sector, are also consider to arrive at a relationship between release rate and dose at exclusion distance. The gamma energy used for computation is 1.28 MeV for Ar-41 and 0.65 MeV for a mixture of Xenon and Krypton isotopes. In order to compute the site specific relationship between release rate and dose the frequency (f)/wind speed (u) (m/s)) for the main sector and the two side sectors are used with which the dose rates are multiplied. Finally all these results are summed up for all weather categories [12]. The dose apportionment for internal irradiators like H-3, I-131 and particulates can be written mathematically as
 (3)
(3)
where, h is Tech spec limit, DAC (pub) is the derived air concentration applicable to members of the public corresponding to dose limit of 1 mSv/y and X/Q is the annual average atmospheric dilution factor at the exclusion distance for the critical sector. The X/Q value applicable for the particular stack height at a distance of 1.6 km from the stack and corresponding to the critical sector is used in the calculation of dose apportionment. The derived air concentration (DAC, public) is defined as the ground level air concentration of radionuclides that results the effective dose limit of 1 mSv/y to members of the public from all-important pathways of exposure. The DAC (public) is generally calculated for both adult and infants and the more restrictive of the two are generally used for calculation of the derived limits. The computation of dose for tritium in detail is depicted elsewhere [12].
4.2. Aquatic Discharges
The dose apportionment for radionuclides discharged into the aquatic environment is computed from the technical specifications limit on concentration for gross beta and Tritium. Mathematical models used in dose apportionment for gross beta for the coastal site and for the inland site are given by
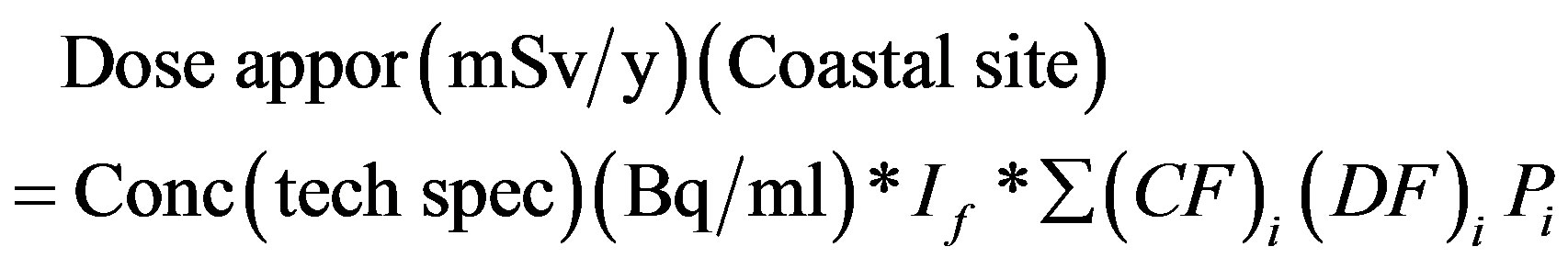 (4)
(4)
where, If is the annual intake of fish by the population for a given NPP site, (g/y), CFi is the concentration factor in marine fish for radionuclide i (ml/g), DFi is the ingestion dose conversion factor for ith radionuclide (Sv/Bq), Pi is the percentage composition of ith radionuclide in the gross activity.
 (5)
(5)
where, Iw is the annual intake of drinking water (ml/y), If is the annual intake of fish by the population for a given NPP site (g/y), CFi is the concentration factor in marine fish for ith radionuclide, DFi is the ingestion dose conversion factor for ith radionuclide (Sv/Bq), Pi is the percentage composition of ith radionuclide in the gross activity.
5. Bootstrap Method in Dose Apportionment
Input data required for computation of dose apportionment is the arithmetic mean value of the radioactive effluents (gaseous and liquid) released into the atmospheric and aquatic environment. The mean value of the released effluent is fed into a standard dose model. Therefore, the mean value of the effluent discharged into the environment is computed from the actual release data. However, in order to compute the average value of a dataset, a-prior knowledge of the population distribution (population refers to a large set of data) of the data set is required; but the population distribution cannot be identified with small dataset. The representative sample size of the existing release data (10 years release data) from nuclear power plant is not sufficient to assume the population as normal distribution. As we do not have the sufficient years of data for concluding a specified probability distribution, we cannot adopt parametric probability distribution for the actual release data. Hence predicting average or median as the representative value of the actual release for proceeding towards the dose apportionment calculation is not at all scientific. So, obviously people will try an adhoc average value of the release based on the actual data. But basically an appropriate scientific method is searched for establishing the dose apportionment. In the new scientific method, bootstrap, the nonparametric method is adopted for identifying the probability distribution of the actual release data [14]. Actual release values for the available number of years are considered as a sample. Bootstrap when applied to the actual samples (say ~10 years release data), produces a large number of release values so called as the population. The sampling without replacement strategy has been implemented for generation of bootstrap samples [15]. Probability density function of the bootstrap generated population is constructed using non-parametric kernel smoothing density method [16-18]. Cumulative distribution function (CDF) has been constructed using the probability density function and the CDF has been used to compute the 99% confidence level (upper confidence limit) of the mean value of the release of the gaseous and liquid effluent [19]. Upper confidence limit of this release value with a defined probability of 0.99 can be accepted as the appropriate limit for establishing the dose apportionment of various nuclear power stations.
6. Results and Discussion
The operating experience of a typical plant #1(considered as an installation in the coastal site) is represented in the form of actual yearly release of gaseous and liquid effluent and the same dataset is as presented in Table 1 and Table 2 respectively. The corresponding distribution of the gaseous and liquid effluent released from the specific nuclear power plant is as shown in Figures 1 and 2. It can be easily investigated from Figures 1 and 2 that arithmetic mean or simple average of the actual release is not the representative input for the estimation of the dose apportioned for the specified nuclide for that specific plant because the shape of distribution of the release data is not the normal distribution. It is confirmed by carrying out the normality test (Kolmogorov-Smirnov Test) [20] of the represented data (Tables 1 and 2); the test fails confirming that the distribution of these data is not normal. Moreover,
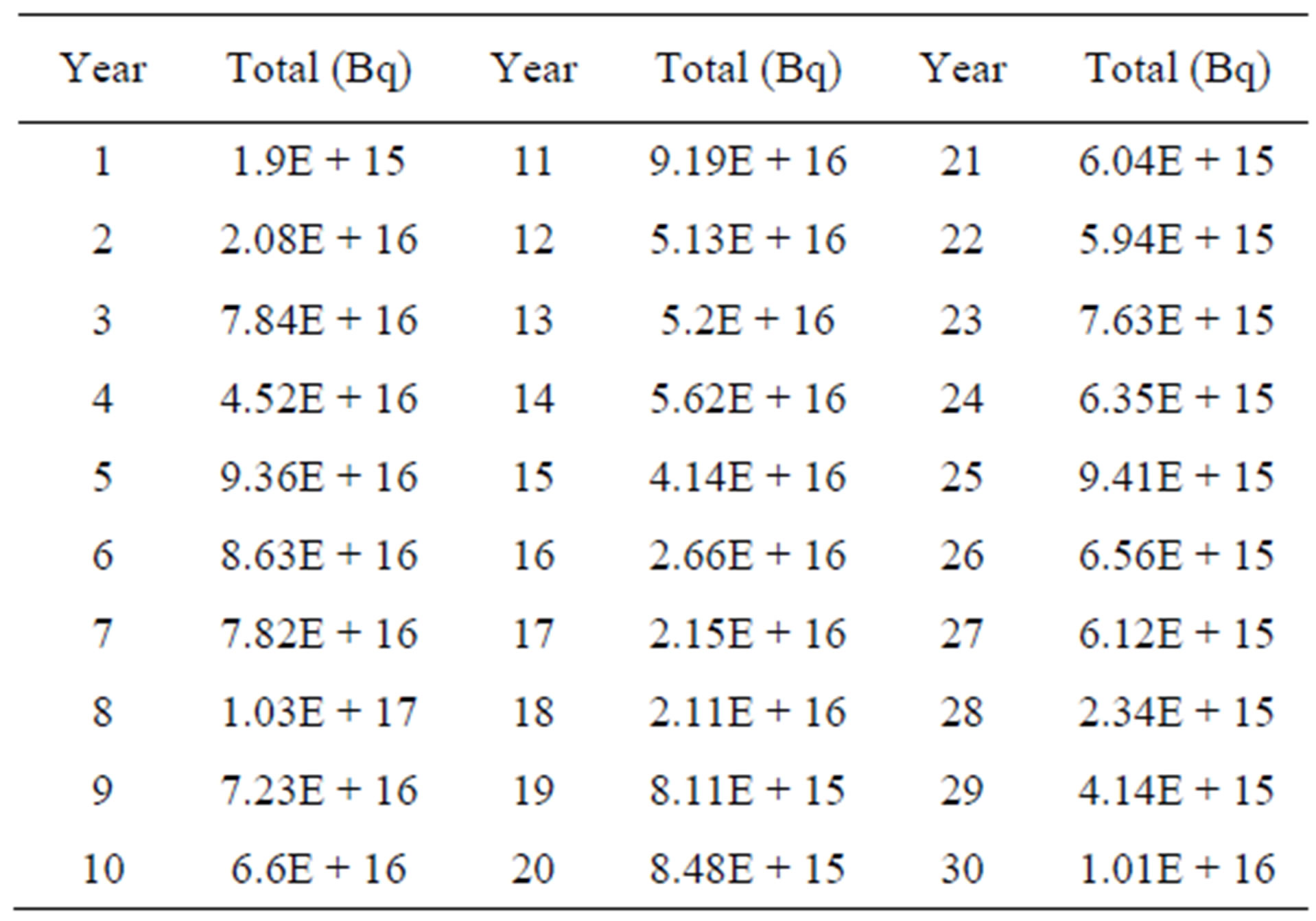
Table 1. Yearly actual release values of gaseous effluent (plant #1).

Table 2. Yearly actual release values of liquid effluent from a typical plant #1.

Figure 2. Distribution of yearly release of liquid effluent from plant #1.
the represented data being a time series one cannot simply take the mean without appropriate trend analysis. In order to overcome this difficulty, bootstrap method has been applied on the data set to construct the population distribution associated with the represented data. The frequency distribution of the release data after bootstrap (histogram) is shown in Figure 3 and corresponding cumulative distribution plot is as shown in Figure 4. Cumulative distribution provides the knowledge of 5th and 95th percentiles of the probability density of release data set. Upper confidence limit as 95th percentiles estimated from uncertainty analysis of the effluent released data is accepted as the appropriate input for dose apportionment calculation Figures 5 and 6 represent the frequency distribution (histogram) and the corresponding cumulative distribution of the gross beta release from plant #1. Cumulative distribution is then utilized to estimate the 5th, 50th and 95th percentiles of the release of the gaseous and liquid effluents from the plant #1.
The 95th percentiles value of the released gaseous and liquid effluent are used as the discharge limit for computing the corresponding apportioned dose for the representtative nuclide (Fission product Noble Gas (FPNG) and gross beta) for the plant #1. Results of the uncertainty estimates of both the FPNG and gross beta release from plant #1 is represented in Table 3. Basically dose apportionment for atmospheric release FPNG is the important and for the aquatic environment gross beta is important. Results from Table 3 indicate that apportioned dose for atmospheric route is more than aquatic route. In order to have the probability density function of the population distribution of the actual release data for tritium in air and tritium in liquid similar approach of bootstrap is adopted. Operating experience of another nuclear power plant, Plant #2 (considered as an installation in the inland site) is taken

Figure 3. Population distribution of FPNG release from plant #1 after bootstrap (sample size of bootstrap: 100,000).

Figure 4. Cumulative distribution of FPNG release from plant #1.
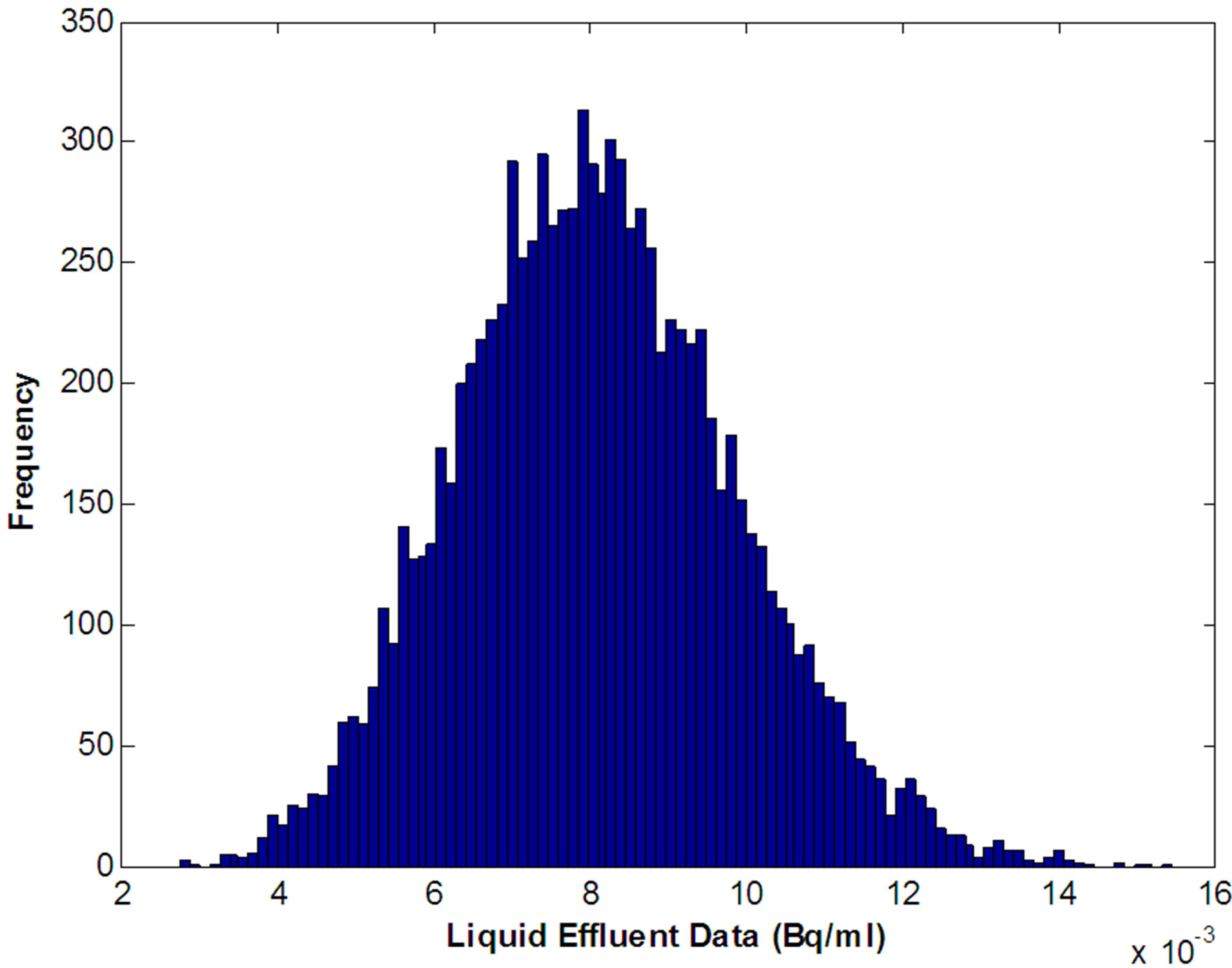
Figure 5. Population distribution of gross beta release from plant #1 after bootstrap (bootstrap sample size taken: 100,000).

Figure 6. Cumulative distribution of gross beta release from plant #1.

Table 3. Uncertainty estimate of gaseous and liquid effluent release from plant #1.
into consideration for this case study. Uncertainty estimates for distribution of each radionuclide using same methodology are tabulated in Table 4. Site specific value of the atmospheric average dilution factor (X/Q), Condenser cooling water (CCW) flow for dilution in the aquatic route, DAC (public), composition of radionuclide for gross beta, concentration factors, intake of fish and the drinking water are used as input for dose calculation. All the required input parameters are listed in Table 5. Apportioned dose using the input parameters listed in Table 5 and 95th percentile value of FPNG and Gross Beta from plant #1 (coastal site) and that of FPNG, H-3 (air), H-3 (liquid) and gross beta from plant #2 are computed and the results are tabulated in Table 6. Comparative study of the dose apportioned for plant #1 and plant #2 from Table 6 indicate that apportioned dose for FPNG and gross beta for plant at coastal site is more than for plant at inland site. Tritium in air and in aquatic environment for plant #1 is not representative because plant #1 is of boiling water type nuclear reactor.
7. Conclusion
Bootstrap technique has been applied to identify the probability density of the population distribution of the gaseous and liquid effluent. Uncertainty analysis of the effluent dataset has been carried to compute the 95th percenttile of the effluent released from the plant. This 95th percen-

Table 4. Uncertainty estimate of Gaseous and Liquid Effluent Release from Plant #2.

Table 5. Input Parameters used for dose computation.

Table 6. Computed Apportioned Dose for Plant #1 and Plant #2.
tile value is used as the discharge limit of the effluent and using this 95th percentile as an input to the standard dose assessment model, dose computation has been carried out. Final conclusion is that bootstrap provides a scientific basis of dose apportionment scheme. It can be further concluded that uncertainty analysis of the effluent data only is essential for estimating the apportioned dose to a nuclear facility. However, an optimization approach is essential when dose apportionment is required for many more plants located at the same site. Research is being continued to develop an optimization technique for this purpose.
REFERENCES
- B. Efron and R. J. Tibshirani, “An Introduction to the Bootstrap,” Chapman and Hall, New York, 1993.
- “International Commission on Radiological Protection, 1990 Recommendations of the International Commission on Radiological Protection,” ICRP Publication 60, Pergamon Press, Oxford and New York, 1991.
- M. Balonov, G. Linsley, D. Louvat, C. Robinson and T. Cabianca, “The IAEA Standards for the Radioactive Discharge Control: Present Status and Future Development,” Radioprotection, Vol. 40, Suppl. 1, S721-S726, 2005. doi:10.1051/radiopro:2005s1-105
- International Atomic Energy Agency, “Regulatory Control of Radioactive Discharges to the Environment,” Safety Standards Series No. WS-G-2.3, IAEA, Vienna, 2000.
- M. R. Chernick, “Bootstrap Methods, A Practitioner’s Guide,” Wiley, New York, 1999.
- P. Hall, “The Bootstrap and Edgeworth Expansion,” Springer-Verlag, New York, 1992.
- G. Archer and J. M. Giovannoni, “Statistical Analysis with Bootstrap Diagnostics of Atmospheric Pollutants Predicted in the APSIS Experiment,” Water, Air, and Soil Pollution, Vol. 106, No. 1-2, 1998, pp. 43-81. doi:10.1023/A:1005004022883
- A. C. Davison and D. V. Hinkley, “Bootstrap Methods and Their Application,” Cambridge University Press, Cambridge, 1997.
- B. Efron, “The Jackknife, the Bootstrap and Other Resampling Plans,” SIAM, Philadelphia, 1982. doi:10.1137/1.9781611970319
- E. J. Dudewicz, “The Generalized Bootstrap,” In: K.-H. Jöckel, G. Rothe and W. Sendler, Eds., Bootstrapping and Related Techniques, Springer-Verlag, Berlin, 1992, pp. 31-37.
- T. J. DiCiccio and B. Efron, “Bootstrap Confidence Intervals (with Discussion),” Statistical Science, Vol. 11, No. 3, 1996, pp. 189-228.
- International Atomic Energy Agency, “Generic Models for Use in Assessing the Impact of Discharges of Radioactive Substances to the Environment,” Safety Reports Series No. 19, IAEA, Vienna, 2001.
- International Atomic Energy Agency, “Basic Safety Standards Series,” SS No. 115, IAEA, Vienna, 1996.
- A. J. Bailer and J. T. Oris, “Assessing Toxicity of Pollutants in Aquatic Systems,” In: N. Lange, L. Ryan, L. Billard, D. Brillinger, L. Conquest and J. Greenhouse, Eds., Case Studies in Biometry, Wiley, New York, 1994, pp. 25-40.
- R. L. Cooley, “Confidence Intervals for Groundwater Models Using Linearization, Likelihood, and Bootstrap Methods,” Ground Water, Vol. 35, No. 5, 1997, pp. 869-880. doi:10.1111/j.1745-6584.1997.tb00155.x
- J. S. U. Hjorth, “Computer Intensive Statistical Methods —Validation Model Selection and Bootstrap,” Chapman and Hall, New York, 1994.
- C. Davison and D. Y. Hinkley, “Bootstrap Methods and Their Application,” Cambridge University Press, Cambridge, 1997.
- R. LePage and L. Billard, “Exploring the Limits of Bootstrap,” John Wiley, New York, 1992.
- P. Barbe and P. Bertail, “The Weighted Bootstrap (Lecture Notes in Statistics),” Springer-Verlag, New York, 1995.
- M. H. DeGroot, “Probability and Statistics,” 3rd Edition, Reading, Addison-Wesley, Boston, 1991.

