American Journal of Operations Research
Vol.05 No.05(2015), Article ID:59443,16 pages
10.4236/ajor.2015.55032
Using Malmquist Index Approach to Measure Productivity Change of a Jordanian Company for Plastic Industries
Abbas Al-Refaie, Mohammad D. Al-Tahat, Ruba Najdawi
Department of Industrial Engineering, University of Jordan, Amman, Jordan
Email: abbas.alrefai@ju.edu.jo, altahat@ju.edu.jo
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 August 2015; accepted 5 September 2015; published 8 September 2015
ABSTRACT
Measurement of a production unit-performance is crucial in determining whether it has achieved its objectives or not, and it generates a phase of management process that consists of feedback motivation phases. The purpose of this paper is to analyze the growth potentials of five production machines in a Jordanian company for plastic industries by employing the non-parametric Malmquist productivity index (MPI) over the period from February to July 2014 in both day and night shifts. The productivity change is decomposed into technical efficiency change (TEC) and technological change (TC). Inefficiency values are observed in each period. The percentage of input utilization is determined in all periods. Then, the Malmquist productivity index (MPI) values are calculated for all periods. Finally, comparisons of TEC, TC and MPI are conducted among the five machines and between the day and night shifts for each machine. The MPI results indicate that the needs for internal training, effective operating procedures, and enhancing quality procedures are required to increase the technical efficiency. On the other hand, figuring out more efficient ways of making existing products allowing output to grow at a faster rate than economic inputs, like using new technologies, will increase technological change. In conclusions, Malmquist model analysis shall provide valuable reference information to management when evaluating the progress in the performances of production machines in plastic industry.
Keywords:
Malmquist Index, Technical Efficiency, Technological Efficiency, Plastic Industry

1. Introduction
Performance measurement of a production unit is crucial in determining whether it has achieved its objectives or not, improving production efficiency, and dealing with internal or external pressures by monitoring and benchmarking a company’s production [1] - [7] .
Malmquist productivity index (MPI) proposed is a management tool used to evaluate the productivity progress for multi-inputs and multi-outputs [8] - [12] . The MPI represents Total Factor Productivity (TFP) growth of a Decision Making Unit (DMU) and reflects the increase or decrease in efficiency with progress or regress of the frontier technology over time under multiple inputs and multiple outputs framework [13] - [15] . The TFP index can be used to estimate the productivity change, which is decomposed into efficiency change and technological change. The concept of productivity usually referred to labor productivity, this concept is very much related to TFP, defined as the product of efficiency change (catch-up) and technological change (frontier-shift). If TFP value is greater than one, this indicates a positive TFP growth from period (t) to period (t + 1), whereas a value less than one indicates a decrease in TFP growth or performance relative to the previous year. The framework employed in Malmquist can be illustrated in Figure 1, where a production frontier representing the efficient level of output (y) that can be produced from a given level of input (x) is constructed. The assumption made is that the frontier can shift over time. The frontier obtained in the current (t) and future (t + 1) time periods is labeled accordingly. When inefficiency exists, the relative movement of any given DMU over time will, therefore, depend on both its position relative to the corresponding frontier (technical efficiency) and the position of the frontier itself (technical change). If the inefficiency is ignored, then the productivity growth over time will be unable to distinguish between improvements that derive from a DMU catching up to its own frontier, or those that result from the frontier itself shifting up over time.
The input-based Malmquist productivity change index is formulated as [16] :
 (1)
(1)
where M is the productivity of the most recent production point 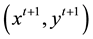 using the period t + 1 technology relative to the earlier production point
using the period t + 1 technology relative to the earlier production point 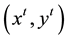 using period t technology, D is input distance functions, the subscript I indicates CCR input-orientation. A value of
using period t technology, D is input distance functions, the subscript I indicates CCR input-orientation. A value of 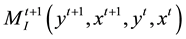 greater than unity indicates a
greater than unity indicates a
positive total factor productivity growth between the two periods. Alternatively,
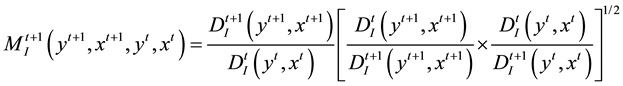 (2)
(2)
In other words, the Malmquist index is
 (3)
(3)
The technical efficiency change (TEC) is given by:
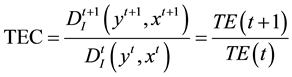 (4)
(4)
Figure 1. Productivity changes over time.
where TE(t + 1) and TE(t) represent the technical efficiency at period (t + 1) and (t) respectively and can be calculated using the DEA model in Equation (5).
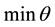 (5)
(5)
Subject to:
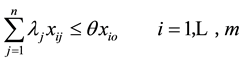 (5a)
(5a)
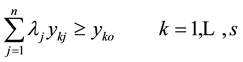 (5b)
(5b)
 (5c)
(5c)
where 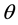 represents the technical efficiency score of unit DMUo and
represents the technical efficiency score of unit DMUo and 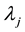 represents the dual variables that identify the benchmarks for inefficient units. Also, the technological change (TC) is formulated as:
represents the dual variables that identify the benchmarks for inefficient units. Also, the technological change (TC) is formulated as:
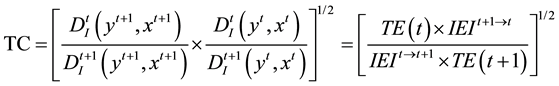 (6)
(6)
where 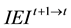 and
and 

Subject to:



Also,

Subject to:



In Equation (2), the TFP index is the product of a measure of technical progress (Technological Change) as measured by shifts in the frontier measured at period t + 1 and period t (averaged geometrically) and a change in efficiency (Efficiency Change) over the same period. Technical efficiency refers to the ability to use a minimal amount of input to make a given level of output. If an organization fails to achieve an output combination on its production possibility frontier, and fails beneath this frontier, it can be said to be technically inefficient. Over time the level of output an organization is capable of producing will increase due to technological changes that affect the ability to optimally combine inputs and outputs. These technological changes cause the production possibility frontier to shift upward, as more outputs are obtainable from the same level of inputs. Thus, for any organization in an industry, productivity improvements over time (more outputs for the same or lower level of inputs) may be either technical efficiency improvements (catching up with their own frontier) or technological improvements (the frontier is shifting up over time) or both. Considering the Constant return to scale (CRS) and variable return to scale (VRS) models will result in four efficiencies: technical efficiency change (TEC), technological change (TC), pure technical efficiency change (PTEC), scale efficiency change (SEC), where all of which will be combined together in the total factor productivity change (TFPC).
Plastics are one of the most used materials on a volume basis in countries’ industrial and commercial life. Plastics are broadly integrated in today’s life style and make a major, irreplaceable contribution to virtually all product areas. A Jordanian company specialized in the production of plastic containers and covers used in food, oil and cosmetics production is interested to assess the performance of its production line during a given period of time. The company started its first production using one injection machine. In order to satisfy the growing demand, it has widened its production with more injection and blowing machines. Currently, the production plant has two types of machines: injection and five blowing machines. The company aims to measure and evaluate the productivity change of five production machines of the same type (blowing machines) M1, M2, M3, M4 and M5 in the company over the period from February to July 2014. This paper, therefore, utilizes Malmquist productivity index to assess the total factor productivity change of the five production machines. The results of this research provide valuable feedback to top managers regarding current improvement decisions and suggest guidelines to future planning. The remaining of this paper including the introduction is organized as follows. Section two describes the data collection and application of MPI. Section three conducts MPI analysis. Section four presents the results and discussions of MPI. The last section concludes the paper.
2. Ease of Use
Figure 2 presents samples of the studied plastic products (covers, pets and containers). The production operation for producing several plastic products in a Jordanian company for plastic industries is depicted in Figure 3.
The data were obtained from the production report over a period of six months (February-2014 to July-2014) for both day and night shifts for the five blowing machine; (M1-M5). Data includes the planned production in units (PP), defect quantity in units (DQ), and idle time in units (IT) and are selected as inputs, whereas the actual production quantity in units (PQ) is set output for each period. Each month was divided into two periods; each period consists of two weeks where (H1) represents the first half of the month and (H2) represents the second half of the month. Inputs and outputs data are represented in Tables 1-5 for M1 to M5, respectively. Table 6 lists the descriptive statistics of the inputs and the output for both day and night shifts.
3. MPI Analysis
The input-based Malmquist productivity change index described in Equation (1) is used to analyze the perfor-
Figure 2. Sample of plastic products.
Figure 3. Production operations of plastic products.
Table 1. The inputs and output data for M1.
Table 2. The inputs and output data for M2.
mance of the five blowing machines over the period from February to July 2014 in both day and night shift. Firstly, the TE are calculated and presented for the five blowing machines in Table 7.
In Table 7 the TE value (= 0.9771) of the first half of February (Feb. H1) for M1 at day work (M1d1) is calculated using Equation (5) as follows:
Table 3. The inputs and output data for M3.
Table 4. The inputs and output data for M4.
Subject to:
Table 5. The inputs and output data for M5.
Table 6. Descriptive statistics of inputs and output.
Table 7. The TE values for machines M1-M5.
Similarly, the TE value (= 0.6394) for M1 in Feb. H2 day working (M1d2) is estimated as follows:
Subject to:
The TE values of the other periods for M1 at day and night shifts are estimated similarly. The TE values at day and night shifts for the other blowing machines (M2-M5) over the period from February-July 2014 are calculated in a similar manner and are also presented in Table 7.
Secondly, the 



Table 8. The estimated 
Table 9. Inputs and output data for calculation of 

Subject to:
Subject to:
The remaining 

Utilizing the results displayed in Table 7 and Table 8, the MPI values are calculated as follows. At beginning, the values of technical efficiency change (TEC), which measures the change in efficiency between current (t) and next (t + 1) periods, are estimated.
For example, the TEC value between the first half of February (Feb. H1) and the second half of February (Feb. H2) for M1d is calculated by applying Equation (4) as follows:
The TEC values of M1 for the other periods and the blowing machines from M1-M5 are calculated then presented in Table 10. Next, the technological change (TC) values are calculated for all periods. The TC is the development of new products or the development of new technologies that allows methods of production to improve and results in the shifting upwards of the production frontier as more outputs are obtainable from the same level of inputs. The TC includes new production processes, called process innovation, and the discovery of new
Table 10. The calculated TEC, TC and MPI values at day shift.
products called product innovation. For illustration, the TC value (= 0.9864) between the first half of February (Feb. H1) and the second half of February (Feb. H2) for M1d is calculated by applying Equation (6) as the following:
The calculated TC values for the blowing machines from M1-M5 are calculated in a similar manner and are also presented in Table 10. Finally, the MPI is used to measure the productivity change of a DMU over time and is calculated by the multiplication of TEC and TC of the same period. For example, the MPI value (= 0.6544) between the first half of February (Feb. H1) and the second half of February (Feb. H2) for M1d is calculated using Equation (2) as follows:
The MPI values for all of the blowing machines at day shift from (M1-M5) are calculated in a similar manner and are displayed in Table 10. Moreover, the TC, TEC and MPI values for all of the blowing machines (M1-M5) are calculated using the data of night shift and then shown in Table 11.
4. Results and Discussions of MPI
4.1. Results and Discussion of TEC, TC and MPI
From Table 10 and Table 11, which present the results of TEC, TC and MPI for the five blowing machines in day and night shifts, the following results are obtained:
In both tables, the coefficient of variation (CV), which equals geometric average divided by standard deviation, is larger than (5%) for TC, TEC and MPI in all machines in day shift. This result indicates that the dispersion is significant and there is a trend in TC, TEC, and MPI. For illustration, the minimum value of TEC for M1 during the whole period in the day shift was (0.6544), the maximum value for it during the whole period was (1.4983), the standard deviation was (0.2200) and the coefficient of variation was larger than (5%) which means
Table 11. The estimated TEC, TC and MPI values at night shift.
that the dispersion is significant and there is a trend in TEC for M1 in day shift.
In Table 10, the M1 has the largest geometric average of MPI (1.0435) with a growth of 4.35% among the five machines in the day shift. This productivity increase is entirely attributed to technological change growth of 4.85% (1 - 1.0485), because the mean technical efficiency regresses by 0.47% (1 - 0.9953) over the whole period. M2 has a geometric average MPI decrease of 2.36% over the same period, this productivity decrease was entirely attributed to technological change regress of 2.36%, while the mean technical efficiency change held constant.
M3 corresponds to the lowest geometric average of MPI over the five blowing machines, it performed the worst with aggregate decrease of 5.32% over this period in the day shift; this productivity decrease stems from the poor performance in technical efficiency change with a regress of 6.65%, while the technological change had a growth of 1.42%. M4 has also geometric average of MPI decrease of 3.57%, over the same period, this productivity decrease is attributed to technological change regress of 4.48%, while the technical efficiency change had a growth of 0.95%. Finally M5 had a large geometric average MPI growth of 3.25% but this growth was lower than the one for M1, this productivity increase was attributed almost equally to both technical efficiency change and technological change of 2.02% and 3.25%, respectively. In Table 11, M4 has the largest geometric average of MPI with a growth of 9.9%, among the five machines in the night shift. This productivity increase is attributed to a growth of both technical efficiency change and technological change of 0.11% and 9.9%, respectively. However, M2 has the lowest geometric average of MPI over the five blowing machines it performed the worst with aggregate decrease of 17.4% over the same period in the night shift; this productivity decrease stemmed from the poor performance of both technical efficiency change with a regress of 0.48%, and technological change regress of 17%. M1 has geometric average MPI regress of 3.4% over the same period; this productivity decrease is attributed to technological change regress of 3.82%, while there is a mean technical efficiency growth of 0.44%. M3 has also geometric average of MPI decrease of 13.8% over the same period, this productivity decrease is attributed to both technical efficiency change regress of 3.13% and technological change regress of 11.02%. Finally, M5 has a geometric average of MPI decrease attributed to both technical efficiency change and technological change regress of 1.08% and 0.5%, respectively.
4.2. Comparison of Results between Day and Night Shifts
Figure 4 and Figure 5 represent the geometric average value of TEC for the five blowing machines in the day
Figure 4. The comparison of TEC values for blowing Machines at day shift.
Figure 5. The comparison of TEC values for blowing Machines at night shift.
and night shifts over the period from February-July 2014, respectively. It is seen in Figure 4 that M5 has the largest geometric average value of TEC (=1.0202) over the period February-July 2014, followed by M4 and M2 with values of 1.009 and 1.0000, respectively. Hence, M2 and M4 are considered efficient. However, M1 and M3 have average values, which are less than one, of 0.9953 and 0.9335, respectively. For the night shift, the geometric average values of TEC in Figure 5 for M1 and M4 are 1.0044 and 1.0011, respectively. However, average values of TEC for M2, M3, and M5 are 0.9952, 0.9687, and 0.9892, respectively. Consequently, M1 and M4 are considered efficient, whereas M2, M3, and M5 are considered inefficient.
In Figure 6 for the day shift, the geometric average values of TC for M1 (1.0485), M3 (1.0142), and M5 (=1.0121) are greater than one. However, the average values of TC for M1 (0.9764) and M4 (0.9552) are smaller than one. For the night shift as shown in Figure 7, only M4 has a geometric average value of TC (1.0977) larger than one over the period February-July 2014. In contrast, average values of TC for M5 (0.9950), M1 (0.9618), M3 (0.8898), and M2 (0.8300) are smaller than one. Finally, the geometric average value of MPI for the five blowing machines at day and night shifts are depicted in Figure 8 and Figure 9, respectively.
Table 12 represents the values for TEC, TC and MPI progress or regress for the five blowing machines over the period (February-July 2014) for both day and night shifts, the number between two parentheses represent the values of TEC, TC and MPI for the night shift while the other numbers represent the values of TEC, TC and MPI for the day shift. The results in Table 12 provide valuable feedback to production/planning managers in setting proactive/corrective actions and improvement plans. Finally, comparisons are conducted between MPI values for each of the blowing machines (M-M5) at day and night shifts as shown in Figure 10. The differences of the MPI values between day and night shifts are displayed in Table 13 for all machines.
In Table 13 for M1, it is noticed that there are significant MPI differences between day and night shifts in all
Table 12. The calculated TEC, TC and MPI values for the five blowing machines at day (night) shift.
Table 13. The MPI differences between day and night shifts.
Figure 6. The comparison of TC values for blowing machines at day shift.
Figure 7. The comparison of TC values for blowing machines at night shift.
Figure 8. The estimated MPI values at the day shift.
periods; except in Jun. H2-Jul.H1 (0.0226). The largest (smallest) difference is 1.5476 (−1.3668) which corresponds to period Apr. H1-Apr. H2 (Feb. H1-Feb. H2). The MPI values for the day shifts increases from −0.3668 to 1.5476 in Feb. H1-Feb. H2 to Apr. H1-Apr. H2. That is, there exists a regress in the performance of the
Figure 9. The estimated MPI values at the night shift.
Figure 10. The comparison of MPI values between day and night shifts for each machine.
night shift compared with day shift. Then, the MPI values for the night shift outperform these for the day shift during Apr. H2-May H1 to May H2-Jun. H1. Finally, the difference decreases from Jun. H1-Jun. H2 to Jul. H1-Jul. H2. For M2-M5, the differences can be analyzed similarly. Moreover, slight MPI differences are observed between day and night shifts in most periods for M3 to M5.
4.3. Implications
Technical efficiency change (TEC) refers to the ability to use a minimal amount of planned production, defect quantity and the idle time to make a given level of production quantity. If the company fails to achieve the output combination on its production possibility frontier, and falls beneath this frontier, it is considered technically inefficient. TEC can make use of existing labor, capital, and other economic inputs to produce more output of the same inputs. As more work experience is gained about production, they become more and more efficient. As a result, minor modifications to plant and procedures can contribute to higher levels of productivity.
Further, training new employees and exchanging the experience between experienced employees and newly hired employees has a great influence on productivity improvement. Furthermore, management should revise the hiring policy, incentive programs, and promotion rules to control the employees' turnover rate. Finally, having a reliable quality control system in the company will assure having lower values of defect quantity (DQ). For, the idle time (IT) should be minimized. Interruptions can be caused by confusing or unclear work instructions, incomplete bill of materials, or running out of material. Hence, improving machine reliability and quality using total productive maintenance and quality tools, reducing overproduction and excess inventory, and implementing effective operating procedures help in reducing idle time. On the other hand, technological change (TC) is the development of new products or the development of new technologies that allows methods of production to improve and results in the shifting upwards of the production frontier, as more outputs are obtainable from the same level of inputs. More specifically, technological change includes new production processes, called process innovation and the discovery of new products called product innovation. With process innovation, firms figure out more efficient ways of making existing products allowing output to grow at a faster rate than economic inputs are growing, In the production machines a process innovation entails machines producing more actual production quantity (PQ) at a faster rate than defect quantity (DQ) or idle time in units (IT). Cost of production decline overtime process innovations.
5. Conclusion
This paper assesses the performance of blowing process for plastic industries using Malmquist Index approach during the period from February to July 2014 for both day and night shifts. Five blowing machines are studied. Two primary issues are addressed in the computation of Malmquist indices of productivity growth. The changes in productivity are divided into technical efficiency change (TEC) and technological change (TC). Data include the planned production in units (PP), defect quantity in units (DQ), and idle time in units (IT) and are selected as inputs, whereas the actual production quantity in units (PQ). Inefficiency is observed in each period. The percentage of input utilization is determined in all periods. Then, the Malmquist productivity index (MPI) values are calculated for all periods. Finally, comparisons of TEC, TC and MPI are conducted among the five machines and between the day and night shifts for each machine. It is concluded that: (1) to improve the technical efficiency, a need for internal training, effective operating procedures, and enhancing quality is required, (2) to increase technological change, figuring out more efficient ways of making existing products or using new technologies allowing output to grow at a faster rate than economic inputs is needed, and (3) with the Malmquist productivity index analysis the company is now able to assess the productivity change of the production machines over time. The results of this research will also help decision makers identify the possible causes of decline in productivity within each production machine and guide them in appropriate proactive/corrective plans.
Cite this paper
AbbasAl-Refaie,Mohammad D.Al-Tahat,RubaNajdawi, (2015) Using Malmquist Index Approach to Measure Productivity Change of a Jordanian Company for Plastic Industries. American Journal of Operations Research,05,384-400. doi: 10.4236/ajor.2015.55032
References
- 1. Cooper, W.W., Seiford, L.M. and Kaoru, T. (2000) Data Envelopment Analysis. Kluwer, Boston, MA.
- 2. Charnes, A., Cooper, L.M., Letwin, A.A., et al. (1989) Data Envelopment Analysis. Kluwer, Dordtrecht, The Netherlands.
- 3. Al-Refaie, A. (2011) Optimising Correlated QCHs in Robust Design Using Principal Components Analysis and DEA Techniques. Production Planning and Control, 22, 676-689.
http://dx.doi.org/10.1080/09537287.2010.526652 - 4. Al-Refaie, A. (2009) Optimizing SMT Performance Using Comparisons of Efficiency between Different Systems Technique in DEA. IEEE Transactions on Electronic Packaging Manufacturing, 32, 256-264.
http://dx.doi.org/10.1109/TEPM.2009.2029238 - 5. Al-Refaie, A. (2010) Super-Efficiency DEA Approach for Optimizing Multiple Quality Characteristics in Parameter Design. International Journal of Artificial Life Research, 1, 58-71.
http://dx.doi.org/10.4018/jalr.2010040105 - 6. Al-Refaie, A. and Al-Tahat, M. (2011) Solving the Multi-Response Problem in Taguchi Method by Benevolent Formulation in DEA. Journal of Intelligent Manufacturing, 22, 505-521.
http://dx.doi.org/10.1007/s10845-009-0312-8 - 7. Al-Refaie, A., Fouad, R., Li, M.-H. and Shurrab, M. (2014) Applying Simulation and DEA to Improve Performance of Emergency Department in a Jordanian Hospital. Simulation Modeling Practice and Theory, 41, 59-72.
http://dx.doi.org/10.1016/j.simpat.2013.11.010 - 8. Chen, C.J., Wu, H.L. and Lin, B.W. (2006) Evaluating the Development of High-Tech Industries: Taiwan’s Science Park. Technological Forecasting & Social Change, 73, 452-465.
http://dx.doi.org/10.1016/j.techfore.2005.04.003 - 9. Coelli, T.J. and Rao, D.S. (2005) Total Factor Productivity Growth in Agriculture: A Malmquist Index Analysis of 93 Countries, 1980-2000. Agricultural Economics, 32, 115-134.
http://dx.doi.org/10.1111/j.0169-5150.2004.00018.x - 10. Odeck, J. (2000) Assessing the Relative Efficiency and Productivity Growth of Vehicle Inspection Services: An Application of DEA and Malmquist Indices. European Journal of Operational Research, 126, 501-514.
http://dx.doi.org/10.1016/S0377-2217(99)00305-7 - 11. Worthington, A. (1999) Malmquist Indices of Productivity Change in Australian Financial Services. Journal of International Financial Markets, Institutions and Money, 9, 303-320.
http://dx.doi.org/10.1016/S1042-4431(99)00013-X - 12. Xue, X., Shen, Q., Wang, Y. and Lu, J. (2008) Measuring the Productivity of the Construction Industry in China by Using DEA-Based Malmquist Productivity Indices. Journal of Construction Engineering and Management, 134, 64-71.
http://dx.doi.org/10.1061/(ASCE)0733-9364(2008)134:1(64) - 13. Asmild, M., Paradi, J., Aggarwall, V. and Schaffnit, C. (2004) Combining DEA Window Analysis with the Malmquist Index Approach in a Study of the Canadian Banking Industry. Journal of Productivity Analysis, 21, 67-89.
http://dx.doi.org/10.1023/B:PROD.0000012453.91326.ec - 14. Diskaya, F., Emir, S. and Orhan, N. (2011) Measuring the Technical Efficiency of Telecommunication Sector within Global Crisis: Comparison of G8 Countries and Turkey. Procedia Social and Behavioral Sciences, 24, 206-218.
http://dx.doi.org/10.1016/j.sbspro.2011.09.037 - 15. Jia, Y.P. and Liu, R.Z. (2012) Study of the Energy and Environmental Efficiency of the Chinese Economy Based on a DEA Model. Procedia Environmental Sciences, 13, 2256-2263.
http://dx.doi.org/10.1016/j.proenv.2012.01.214 - 16. Worthington, A. (2000) Technical Efficiency and Technological Change in Australian Building Societies. Abacus, 36, 180-197.
http://dx.doi.org/10.1111/1467-6281.00059








































