American Journal of Operations Research
Vol.4 No.3(2014), Article ID:46002,9 pages
DOI:10.4236/ajor.2014.43016
Reliable Facility Systems Design Subject to Edge Failures: Based on the Uncapacitated Fixed-Charge Location Problem
Yuangang Pan1, Yali Du1, Zongtian Wei2*
1Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an, China
2Department of Mathematics, Xi’an University of Architecture and Technology, Xi’an, China
Email: *ztwei@xauat.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 24 March 2014; revised 24 April 2014; accepted 30 April 2014
ABSTRACT
The reliability of facility location problem has aroused wide concern recently. Many researchers focus on reliable and robust facility systems design under component failures and have obtained promising performance. However, the target and reliability of a facility system are to a large degree adversely affected by the edge failures in the network, which remains a deep study. In this paper, we focus on facility systems’ reliability subject to edge failures. For a facility location system, we formulate two models based on classical uncapacitated fixed-charge location problem under deterministic and stochastic cases. For a specific example, location decisions and the comparison of reliability under different location models are given. Extensive experiments verify that significant improvements in reliability can be attained simply by increasing the amount of operating cost.
Keywords:Facility System, Reliability, Edge Failure, Uncapacitated Fixed-Charge Location Problem

1. Introduction
A facility system can be structured as a connected graph in which the vertices represent entities and the edges represent facilities such as the paths of goods or information [1] . In this paper, we distinguish two kinds of facilities, “vertex facilities” and “edge facilities”. For simplicity, we call them “vertices” and “edges”, respectively.
Every facility system in operation may face various disruptions. Since the facility location decisions are hard to reverse, the location decisions are of great importance and have aroused great attention from researchers and practitioners recently [2] .
While most of the literatures focus on the reliable and robust facility system design and analysis under component failures, the existing works are mainly concentrated on the “node” (e.g. suppliers, distribution centers) losses [3] . Snyder [4] has researched the influence of vertex failure situations. The author formulates Maximum Failure Cost Reliability Models and Expected Failure Cost Reliability Models. But both of the models don’t take the edge failures into consideration, which are more likely to occur in reality.
In most cases, facility system disruptions are caused by the failures of edges, e.g., closure of highway because of the inclement weather, traffic jam, road damage caused by earthquakes or debris flows [5] . Wei et al. [1] formulated two models based on deterministic and stochastic cases to measure the loss in efficiency due to edge failures. But they have not solved the facility location problem, which can help making facility location decisions and has more realistic significance.
Once a facility system is constructed, it’s hardly to inverse. If some failure scenarios occurred, whether you can afford the increase of operating cost is of great significance. No techniques can completely eliminate a loss by reducing the edge loss failure probability to zero, so the location decision making based on the reliability is very important. As far as we know, researchers and practitioners have not paid enough attention to the impact of edge failures on the efficiency of a facility system by so far.
The uncapacitated fixed-charge location problem (UFLP) [6] is a classical combinatorial optimization problem that determines facility locations and assignments of customers to facilities in such a way that the sum of fixed and transportation costs is minimized. We assume that the network is connected after a disruption [7] .
Based on the UFLP model, the main contributions of our work are as follows:
1) We introduce edge failures into the facility location problems to choose the facilities satisfying the reliability requests.
2) Two models based on deterministic and stochastic cases are formulated and the experiment results indicate that under edge failure situations, our models perform better than UFLP.
3) The improved stochastic reliable model is proposed to reduce the calculation amount.
The remainder of this paper is organized as follows: Section 2 introduces the reliability theory. In Section 3, we first introduce the classical uncapacitated fixed-charge location problem, and then propose two reliable location models under deterministic and stochastic situations according to the reliability theory. We use a scenariobased algorithm to compute a specific example. The experimental results and corresponding analysis are presented in Section 4. Finally, we conclude this paper in Section 5.
2. Reliability Theory
In this section, we introduce the reliability theory to facility location problem. Snyder and Daskin [8] define the reliability of a system as the ability of a system to perform well even when parts of the system have failed. Once the facility location decisions are confirmed, the reliability can be treated as an inherent property of the system. It’s related to network reliability theory, which is concerned with calculating or maximizing the probability that a graph remains connected after random failures due to congestion, disruptions, or blockages.
In this paper, the system’s reliability, denoted by , is defined to be the ratio of the system’s
operating cost to the cost after some edges have failed [1] .
, is defined to be the ratio of the system’s
operating cost to the cost after some edges have failed [1] .
3. Reliable Facility Location Models
We view a facility system as a weighted connected simple graph![]() , where
, where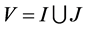 ;
;
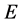 is the edge set with the edges denoting goods or information
paths;
is the edge set with the edges denoting goods or information
paths;
 is the vertex weight set with the weight
is the vertex weight set with the weight
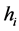 of vertex i, denoting the demand of customer i, and
of vertex i, denoting the demand of customer i, and
 is the edge weight set with the weight
is the edge weight set with the weight
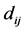 of edge
of edge![]() , denoting the length between
, denoting the length between
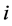 and
and
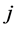 under the existing conditions. By
under the existing conditions. By
 we also denote the shortest path length (or distance) between
we also denote the shortest path length (or distance) between
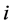 and
and
 if
if![]() .
.
The following are the notations for our formulations.
Sets
 : set of customers, indexed by
: set of customers, indexed by .
.
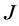 : set of potential facility locations, indexed by
: set of potential facility locations, indexed by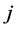 .
.
Parameters
 : demand at customer
: demand at customer .
.
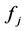 : fixed cost of open a facility at
: fixed cost of open a facility at .
.
 : delivery cost per unit per length.
: delivery cost per unit per length.
The uncapacitated fixed-charge location problem (UFLP) [6] is a classical facility location problem that chooses facility locations and assignments of customers to facilities to minimize the sum of fixed and transportation costs. For simplicity, we call it “cost”.
Assume that
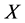 is an feasible solution of the UFLP, i.e.,
is an feasible solution of the UFLP, i.e.,
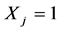 , if a facility is established at location
, if a facility is established at location ; 0,otherwise. The model of UFLP is as
follows:
; 0,otherwise. The model of UFLP is as
follows:
Min
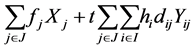 (1)
(1)
s.t. (2)
(2)
 (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
The objective function (1) minimizes the sum of the fixed cost for opening the facilities and the demand weighted total distance. Constraints (2) stipulate that each customer is assigned to exactly one facility, while constraints (3) limit assignments to open sites. Finally, constraints (4) and (5) are integrality constraints.
Let
 be the set of all feasible solutions and
be the set of all feasible solutions and
 be the potential failure edge set, where the edge failure is defined as an edge
losses its designed function completely. Therefore, a failed edge in
be the potential failure edge set, where the edge failure is defined as an edge
losses its designed function completely. Therefore, a failed edge in
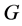 is equivalent to delete (or close) the corresponding line from the facility system.
We also assume that edge failures are independent and multiple edge failures may
occur simultaneously.
is equivalent to delete (or close) the corresponding line from the facility system.
We also assume that edge failures are independent and multiple edge failures may
occur simultaneously.
Considering the edge loss scenarios, we define
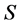 as set of all the edge loss scenarios. We define the edge loss level
as set of all the edge loss scenarios. We define the edge loss level
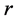
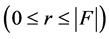 as the number of edges which fail simultaneously. Let
as the number of edges which fail simultaneously. Let
 be the set of scenarios corresponding to the closure or deletion of
be the set of scenarios corresponding to the closure or deletion of
 edges from
edges from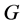 , i.e., every
, i.e., every
 explicitly specifies the failed
explicitly specifies the failed
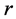 edges in F.
edges in F.
We distinguish two cases: deterministic and stochastic, to formulate the UFLP-based reliability analysis models that evaluate the reliability of a facility system after some edges have failed.
3.1. Deterministic Facility Location Model
During the period of facility location design, the designer will always consider
a question: under a specific edge loss level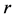 , if a failure scenario happened, the
increased cost of serving all the customer in the network whether can be endured
or not. As to every feasible solution
, if a failure scenario happened, the
increased cost of serving all the customer in the network whether can be endured
or not. As to every feasible solution , we have an operating cost under a specific
scenario
, we have an operating cost under a specific
scenario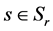 . Under the above consideration, it’s necessary
to consider the worst scenario of every specific feasible solution in
. Under the above consideration, it’s necessary
to consider the worst scenario of every specific feasible solution in
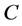 under edge level
under edge level , and find out the lowest cost one.
, and find out the lowest cost one.
We formulate the following deterministic reliability model(DRM) to minimum the maximal
cost under a given edge loss level :
:
 (6)
(6)
s.t.
 (7)
(7)
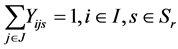 (8)
(8)
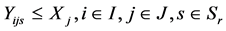 (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
The objective function (6) and (7) minimize the maximum operating cost under the
worst scenario in
 (i.e. (7) restricts the maximum operating cost of the worst scenario under a given
level
(i.e. (7) restricts the maximum operating cost of the worst scenario under a given
level
 and a specific feasible solution
and a specific feasible solution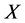 , while (6) minimizes the worst operating
cost of all feasible solutions). Under a specific scenario, constraints (8) stipulate
that each customer is assigned to exactly one facility, while constraints (9) limit
assignments to open sites. Finally, constraints (10) and (11) are integrality constraints.
, while (6) minimizes the worst operating
cost of all feasible solutions). Under a specific scenario, constraints (8) stipulate
that each customer is assigned to exactly one facility, while constraints (9) limit
assignments to open sites. Finally, constraints (10) and (11) are integrality constraints.
3.2. Stochastic Facility Location Model
In section 3.1, we have discussed the case where the loss level is a certainty.
We now consider the case where loss is not a certainty upon an edge failure. Usually,
the chances of losing an edge are based upon some probability. We wish to derive
the expected efficiencies associated with an existing system. To do this we need
to take every scenario and it’s probability into consideration. Let
 be the failure probability of edge
be the failure probability of edge . We denote the set
. We denote the set
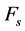 as the failure edge in scenario
as the failure edge in scenario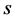 , and
, and
![]() as the probability of scenario
as the probability of scenario .
.
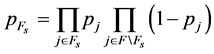 (12)
(12)
We formulate the following stochastic reliability model (SRM):
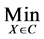
 (13)
(13)
s.t.
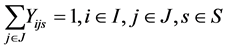 (14)
(14)
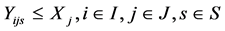 (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
The objective function (13) minimizes the expected operating cost under every possible failure scenario. Constraints (14) stipulate that each customer is assigned to exactly one facility under a specific failure scenario, while constraints (15) limit assignments to open sites. Finally, constraints (16) and (17) are integrality constraints.
3.3. Improvement of the Stochastic Model
In this section, we introduce a new parameter confidence level, indexed by
 which is a predefined number and takes value from (0,1). We introduce the concept
of interval estimation. If there exist two positive integer
which is a predefined number and takes value from (0,1). We introduce the concept
of interval estimation. If there exist two positive integer
![]() which satisfy the equation
which satisfy the equation
![]() (18)
(18)
then we take the probability of
 to fall into
to fall into
![]() as
as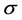 . And the interval
. And the interval
![]() is the interval estimation of
is the interval estimation of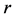 .
.
Noting that the edge loss level
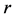 obeys the Multivariate Bernoulli distribution. Given the failure probability, we
can easily get
obeys the Multivariate Bernoulli distribution. Given the failure probability, we
can easily get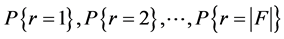 . So it’s easy to get the interval estimation
of
. So it’s easy to get the interval estimation
of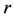 . Considering the low probability of the case when
. Considering the low probability of the case when
 fall into the interval
fall into the interval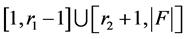 , we take no account of this interval.
Let
, we take no account of this interval.
Let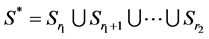 , and the model (13)-(17) can be modified as the improved
stochastic reliability model(ISRM):
, and the model (13)-(17) can be modified as the improved
stochastic reliability model(ISRM):

 (19)
(19)
s.t.
 (20)
(20)
 (21)
(21)
![]() (22)
(22)
 (23)
(23)
The objective function (19) minimizes the expected cost under the scenarios in . Constraints (20) stipulate that each customer is assigned
to exactly one facility under a specific failure scenario, while constraints (21)
limit assignments to open sites. Finally, constraints (22) and (23) are integrality
constraints.
. Constraints (20) stipulate that each customer is assigned
to exactly one facility under a specific failure scenario, while constraints (21)
limit assignments to open sites. Finally, constraints (22) and (23) are integrality
constraints.
Obviously, the main difference between ISRM and SRM is just its neglect of low probability scenarios, which lead to the remarkable reduction in complexity.
4. Experiment and Reliability Analysis
In this section we apply the DRM and the SRM to a data set to get the facility location
decisions and compare them with the classical UFLP. Given the edge loss level , one can easily enumerate each of the possible scenarios
as well as calculate the operating cost under each specific scenario and find out
the worst one. The ratio of systems efficiency and the worst operating cost under
the edge loss level
, one can easily enumerate each of the possible scenarios
as well as calculate the operating cost under each specific scenario and find out
the worst one. The ratio of systems efficiency and the worst operating cost under
the edge loss level
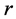 is defined as the systems reliability under a specific level
is defined as the systems reliability under a specific level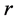 .
.
Obviously the efficiency is measured at 100% if all edges are operating normally. If an edge is lost due to a natural disaster, intentional strike or planned closure, then the shortest paths from facilities to consumers will change, and the delivery scheme should be adjusted simultaneously.
The results of this series of calculations will define a series of reliability from
![]() (i.e. all edges are operating well) to
(i.e. all edges are operating well) to
 (i.e. all edges in
(i.e. all edges in
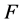 are lost). We can compare the reliability of different facility location models
under different edge loss level. Note that once the facility location has been determined,
we assume that it can’t be reversed.
are lost). We can compare the reliability of different facility location models
under different edge loss level. Note that once the facility location has been determined,
we assume that it can’t be reversed.
Our data set is derived from the 2008 China census data: a 49-node set consisting
of the capitals of all the provinces in China plus the two special administrative
regions Hong Kong and Macao, as well as other 15 big cities [1] . The demand of
city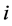 ,
,
 is settled to be the city’s administrative region population
divided by 10000. The transportation links (edges) are set to the recent national
highways and the transportation costs per unit per length through different roads
are all set to
is settled to be the city’s administrative region population
divided by 10000. The transportation links (edges) are set to the recent national
highways and the transportation costs per unit per length through different roads
are all set to . The fixed cost of facilities setup are
estimated by considering the factors such as local labor price, facility size, and
other natural conditions. The potential failure edges set are consisted of 8 edges,
. The fixed cost of facilities setup are
estimated by considering the factors such as local labor price, facility size, and
other natural conditions. The potential failure edges set are consisted of 8 edges,
 . And the corresponding probability are given in Table 1.
. And the corresponding probability are given in Table 1.
By using the above data set we optimally solve a UFLP to site an existing facility
system, the solutions are given in Table 2. In
Table 2, the serving facilities set are fixed as
the optimal solution of UFLP without edge failure. For each loss level, Objec.Value
is the fixed and transportation cost under the worst scenario. The corresponding
failed edges and the reliability are given as well. In
Table 2, column 5 demonstrates that reliability drops down to 79.20% with
the increase of level . And the reliability drops quickly by
17.87% from
. And the reliability drops quickly by
17.87% from
 to
to
 while it drops slowly by 2.93% form
while it drops slowly by 2.93% form
![]() to
to![]() , relatively. From column 2, we find that the edges 2, 4,
5, 7, 8 always appear in the failed edges set, which demonstrate that a minority
of failed edges may play the leading role in system’s reliability.
, relatively. From column 2, we find that the edges 2, 4,
5, 7, 8 always appear in the failed edges set, which demonstrate that a minority
of failed edges may play the leading role in system’s reliability.
In Table 3, column 3 is the location decisions
correspond to the worst scenarios with edge loss levels in column 1. The Objec.Values
in column 4 are fixed and transportation cost under location decisions in column
3 and failed edges in column 2. From column 3, we find that location decisions under
different level
 is very similar to each other, especially when r = 4, 6, 7, 8, the location decisions
are exactly the same. This discovery indicates that the system’s reliability are
affected by some specific serving facilities. When all edges are in operation, the
system’s reliability is measured at 100%. The reliability drops down to 93.11% with
the increase of level
is very similar to each other, especially when r = 4, 6, 7, 8, the location decisions
are exactly the same. This discovery indicates that the system’s reliability are
affected by some specific serving facilities. When all edges are in operation, the
system’s reliability is measured at 100%. The reliability drops down to 93.11% with
the increase of level , and its falling speed exhibits the same
characteristics as that in UFLP(see Table 2), which
slow down gradually.
, and its falling speed exhibits the same
characteristics as that in UFLP(see Table 2), which
slow down gradually.
In Table 4, we use the SRM to find out the optimal
location decisions in column 3. The worst failed edges set are given in column 2.
The reliability’s variation shows the same properties as that of DRM in Table 3. The reliability fall from 100% where no edge losses
to 94.88% where the worst scenario of edge loss level![]() .
.
Table 1. Potential failure edges and probability.
Table 2. Reliability and Objec.Value of UFLP.
Table 3. Reliability and Objec.Value of DRM.
Table 4. Reliability and Objec.Value of SRM.
We compare the reliability and operating cost of UFLP, DRM and SRM in Table 5. From Table 5, we can see:
1) In the deterministic cases, when the edge loss level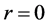 , UFLP and DRM have the same results
of operating cost as 9197100. But under a given edge loss level
, UFLP and DRM have the same results
of operating cost as 9197100. But under a given edge loss level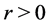 , the operating cost of UFLP will exceed
the cost of DRM, and the reliability of the UFLP will drop dramatically, while that
of DRM drops slightly. For example, when
, the operating cost of UFLP will exceed
the cost of DRM, and the reliability of the UFLP will drop dramatically, while that
of DRM drops slightly. For example, when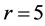 , the costs of UFLP and DRM are 11,413,215
and 9,868,450, while the corresponding reliability is 80.58% and 93.20%.
, the costs of UFLP and DRM are 11,413,215
and 9,868,450, while the corresponding reliability is 80.58% and 93.20%.
2) In the stochastic cases, the decision made by SRM is a little inferior to one chose by classical UFLP on operating cost when all edges are operating well. But once the edge losses occur, the operating cost of UFLP will increase to 11,612,964, and its reliability drops fast to 79.2%. On the contrary, the serving facilities selected by our proposed SRM perform very well. Its cost is only 9903637 and the reliability drops slightly to 94.88%. Both of the cost and the reliability perform better than the classical UFLP. Figure 1 shows the variation of the reliability.
As to the improved stochastic reliability model, Table
6 shows the probability of different edge loss levels. We draw out the probability
distribution of , see Figure 2.
The advantage of our handling is that it can simplify the calculation and we can
get the roughly estimation of operating cost under different edge loss levels. Table 7 gives out the reliability and operating
cost of ISRM.
, see Figure 2.
The advantage of our handling is that it can simplify the calculation and we can
get the roughly estimation of operating cost under different edge loss levels. Table 7 gives out the reliability and operating
cost of ISRM.
5. Summary and Conclusion
In this paper, we propose two types of scenario based facility location models in order to make facility location decisions which can improve the system’s reliability. We distinguish deterministic and stochastic cases to formulate and compute a specific example. We have successfully made the location decisions. Reliability of two different location models is also given and is compared with the classical UFLP model.
1) As to a facilities fixed system, if all edges are in operation, the classical UFLP will get the optimal solution with the lowest operating cost, but once the edge failure situations occur, the operating cost will increase dramatically.
2) Under different location schemes, the edge set which plays the leading role of systems reliability is different. In other words, each edge’s influence on system’s reliability depends on its conjoint facilities.
3) By increasing a small amount of operating cost, we can get a much more reliable location design.
Table 5. Reliability and Objec.Value of UFLP, DRM and SRM.
Table 6. Edge levels and probability.
Table 7. Reliablility and Objec.Value of ISRM.

Figure 1. The edge loss level and reliability.

Figure 2. The probability distribution of level r.
According to the practical situations, our models can be improved in the following ways. Firstly, we assume that the edge failures are independent from each other, but in practice, once an edge failed, the function of its adjacent edges will be impacted. Secondly, we assume that the edges are not limited on transport capacity, which is not real. Thirdly, through our analysis, we also find that under different edge loss levels, the facility location designs don’t differ too much from each other. So the location decisions are relevant to the network’s inherent properties. It’s important to filter out some facilities as the alternative facility set, which can reduce the number of feasible solutions without losing the optimal solution. Thereby, the calculation amount can be reduced a lot. Modeling the reliable facility location problems and related problems under this situation are worthy of study.
Acknowledgements
This work was supported by the national college student innovative entrepreneurial training project (Grant No. 201310699066), NSRP (Grant No. 2012JC2-03) and ESF (Grant No. 12JK0888). The authors are grateful to the anonymous referees of this article.
References
- Wei, Z.T. and Xiao, H.Y. (2011) Reliability Analysis of Facility Systems Subject to Edge Failures: Based on the Uncapacitated Fixed-Charge Location Problem. Open Journal of Discrete Mathematics, 1, 153-159. http://dx.doi.org/10.4236/ojdm.2011.13019
- Wang, M., Wei, Z.T. and He, Y. (2012) Reliability Analysis of Systems Based on the UFLP under Facility Failure and Conditional Supply Cases. Advances in Pure Mathematics, 2, 128-132. http://dx.doi.org/10.4236/apm.2012.22019
- Eiselt, H.A., Gendreau, M. and Laporte, G. (1992) Location of Facilities on a Network Subject to a Single-Edge Failure. Networks, 22, 231-246. http://dx.doi.org/10.1002/net.3230220303
- Snyder, L.V. (2003) Supply Chain Robustness and Reliability: Models and Algorithms. PhD Thesis, Northwestern University, Evanston.
- Wei, Z.T., Xiao, H.Y. and Quan, Y.X. (2011) Analysis of Facility Systems Reliability Subject to Edge Failures: Based on the p-Median Problem. American Journal of Operations Research, 1, 277-283. http://dx.doi.org/10.4236/ajor.2011.14032
- Balinski, M.L. (1965) Integer Programming: Methods, Uses, Computation. Management Science, 12, 253-313. http://dx.doi.org/10.1287/mnsc.12.3.253
- Erlenkotter, D. (1978) A Dual-Based Procedure for Uncapacitated Facility Location. Operations Research, 26, 992- 1009. http://dx.doi.org/10.1287/opre.26.6.992
- Snyder, L.V. and Daskin, M.S. (2005) Reliability Models for Facility Location: The Expected Failure Cost Case. Transportation Science, 39, 400-416. http://dx.doi.org/10.1287/trsc.1040.0107
NOTES

*Corresponding author.


