American Journal of Operations Research
Vol. 2 No. 4 (2012) , Article ID: 25148 , 10 pages DOI:10.4236/ajor.2012.24060
Performance Analysis of Two Priority Queuing Systems in Tandem
College of Technological Innovation, Zayed University, Dubai, UAE
Email: faouzi.kamoun@zu.ac.ae
Received September 19, 2012; revised October 22, 2012; accepted November 2, 2012
Keywords: Priority Queuing System; Tandem Queues; Performance Analysis; Discrete-Time Queues
ABSTRACT
In this paper, we consider a tandem of two head-of-line (HOL) non-preemptive priority queuing systems, each with a single server and a deterministic service-time. Two classes of traffic are considered, namely high priority and low priority traffic. By means of a generating function approach, we present a technique to derive closed-form expressions for the mean buffer occupancy at each node and mean delay. Finally, we illustrate our solution technique with some numerical examples, whereby we illustrate the starvation impact of the HOL priority scheduling discipline on the performance of the low-priority traffic stream. Our research highlights the important fact that the unfairness of the HOL priority scheduling becomes even more noticeable at the network level. Thus this priority mechanism should be used with caution.
1. Introduction
In this contribution, we consider two discrete-time priority queuing systems (hereafter referred to as PQS1 and PQS2) in tandem. Each PQS implements a non-preemptive head-of-line (HOL) priority scheduling with a single server. We consider two types of priority customers, namely high-priority and low priority customers (hereafter referred to as class-1 and class-2, respectively). The number of class-1 and class-2 arrivals within a slot can be correlated random variables.
The main thrust behind our interest to explore the performance of tandem priority queues is that previous studies have focused on an isolated priority queuing system. However, it is well known that in a typical (store and forward) network environment, customers go through a number of switching nodes before reaching their final destinations. For instance, customers belonging to a virtual connection are stored and forwarded through a number of queues in tandem. Similarly, in many manufacturing and service applications (including health-care and banking), customers (or jobs) need to go through a number of prioritized service facilities before completing a single transaction. At the same time, none of the previous studies on tandem queues have considered multi-class priority scheduling schemes. It is well known however that next generation telecommunications networks are being built around the inspiration of having a single costeffective packet-based network that is capable of supporting diverse classes of services, each with its own Quality of Service (QoS) requirement. For instance, realtime traffic is delay and delay-jitter sensitive, while nonreal-time applications are mainly loss sensitive. To achieve this goal, various packet service disciplines that determine the order by which customers are served have been proposed. Among the simplest time-priority scheduling schemes, the non-preemptive head-of-line (HOL) priority scheduling discipline has been proposed to provide differentiated services to the high-priority traffic class. Under this scheme, the server always schedules the delaysensitive traffic first (if present). Many previous studies (see for example [1-4]) have analyzed the performance of discrete-time HOL-priority queuing systems (in terms of system content and/or customer delay) under various assumptions regarding the arrival and service time distributions. In particular, Walraevens et al. [5] analyzed a single server discrete-time HOL priority queuing system in steady-state. The corresponding transient results were reported in [6], while the case of multi-server HOL priority queue is treated in [7]. In [8], Walraevens et al. analyzed the busy periods and the output characteristics of a HOL priority queue. Kamoun [9] analyzed a HOL priority queuing system which is subjected to a Markovian interruption process. However, to our best knowledge, none of the previous contributions addressed the case where customers have to go through more than one priority queuing stage.
The contribution of this paper consists of the practical queuing model being considered, the solution technique being developed to extract explicit expressions for the various performance measures, and the new insights provided on the performance of HOL priority queuing systems in a small “network” environment:
First, we add to the existing literature on non-preemptive priority models by considering two priority-based queuing systems in tandem. This tandem configuration of two PQS stages makes the resulting model more practical and flexible in studying more realistic priority-based queuing systems.
Second, we demonstrate how a generating function can be used to derive closed-form expressions for the mean buffer occupancies and mean delays. The closedform expressions of these performance measures make it very convenient to understand the effect of various system parameters on the performance of both traffic types. In particular, this research demonstrates how the starvation of the low-priority traffic, due to the HOL priority scheduling discipline, is particularly accentuated at the second stage. Our approach also bypasses the need to characterize or approximate the output process of the first PQS stage. Last, the exact expressions for some key performance measures can also be used as baselines to validate the accuracy of potential approximation techniques.
The remainder of this paper is organized as follows: In Sections 2 and 3, we describe the queuing model and derive an expression for the Joint Probability Generating Function (JPGF) of the system state vector. In Section 4, we derive explicit expressions for some boundary terms appearing in the JPGF. From this JPGF, the marginal PGFs of the system contents at three of the four nodes, as well as several other JPGFs are derived, as illustrated in Section 5. Closed-form expressions for the first moments of the system contents and customer delay are presented in Section 6. Numerical results that provide insights into the behavior of the queuing model are provided in Section 7. In particular, we wanted to further explore the impact of the HOL priority scheduling discipline in a tandem configuration on the performance of class-1 and class-2 customers. Finally, a summary of the main findings of the papers and some suggestions for further research are provided in Section 8.
2. Analytical Model Description
We consider two discrete-time priority queuing systems (PQS) in a tandem configuration. Each PQS has an infinite storage capacity and a single (FCFS) server. The time axis is divided into equal length slots and customer service completion is synchronized to occur at the slot boundaries. Here a slot is the time period required to transmit exactly one customer from the system. It is assumed that a customer which arrives during a slot cannot be served before the beginning of the next slot. A “conceptual” diagram for our queuing model is depicted in Figure 1.
As shown in Figure 1, in each PQS, customers are served based on a HOL time-priority scheme, whereby type-1 customers have absolute non-preemptive priority over type-2 customers. Under this priority scheme, the server will always serve type-1 customers (if any). If there are no type-1 customers, then type-2 customers (if any) will be served. The model shown in Figure 1 can be viewed as two HOL priority queuing systems cascaded in tandem (PQS1 and PQS 2), or as two parallel tandem queuing systems, which are coupled. In the latter case, the first tandem system consist of two high-priority queues (nodes 1 and 3), while the second system consists of the two low-priority queues (nodes 2 and 4). We also note that the input to the high/low priority queues (node 3/4 in PQS 2) consists of new type 1/2 customers joining the network (exogenous arrivals), as well as type 1/2 customers which completed service at the first PQS. It is also clear from the model description that the high-priority traffic stream, traversing nodes 1 and 3, is not interrupted by the HOL priority scheduling mechanism. The low-priority traffic stream, on the other hand, is subjected to two interruptions, at nodes 2 and 4. It is also assumed that inter-stage departures are not allowed.
In the sequel, we denote the number of arrivals of class-j customers to PQS 1 during slot k by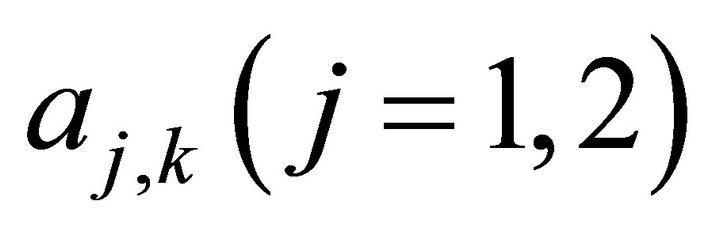 . These arrivals constitute a series of i.i.d. random variables with the common joint probability generating function
. These arrivals constitute a series of i.i.d. random variables with the common joint probability generating function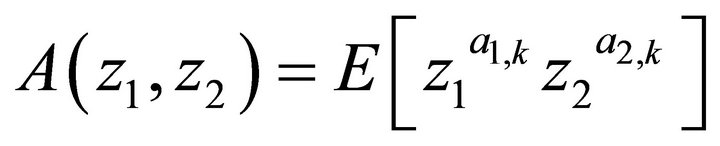 , independent of k. We define the marginal pgfs of the arrivals to PQS 1 from class-1 and class-2 customers during a slot by
, independent of k. We define the marginal pgfs of the arrivals to PQS 1 from class-1 and class-2 customers during a slot by
 and
and 
respectively.
The marginal arrival rates of class-j (j = 1, 2) to PQS 1 are denoted by . We further denote the total number of arriving customers to PQS 1 during slot kby
. We further denote the total number of arriving customers to PQS 1 during slot kby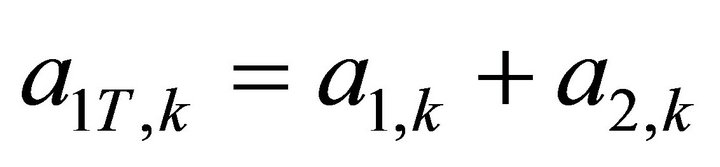 , with corresponding pgf
, with corresponding pgf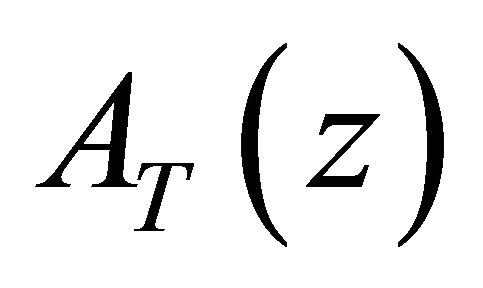 . The total arrival rate to PQS 1 is denoted
. The total arrival rate to PQS 1 is denoted
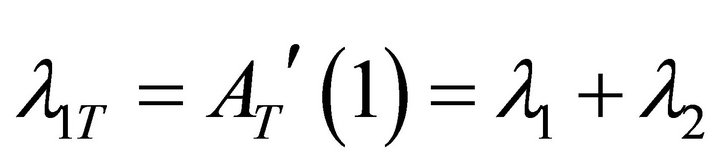 . Similarly, we denote the number
. Similarly, we denote the number
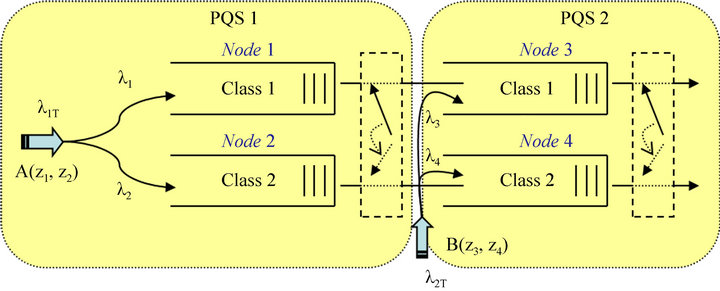
Figure 1. Conceptual diagram of the tandem queuing model with HOL priority.
of “exogenous” arrivals of class-j customers to PQS 2 during slot k by . These arrivals constitute a series of i.i.d. random variables with the common joint probability generating function
. These arrivals constitute a series of i.i.d. random variables with the common joint probability generating function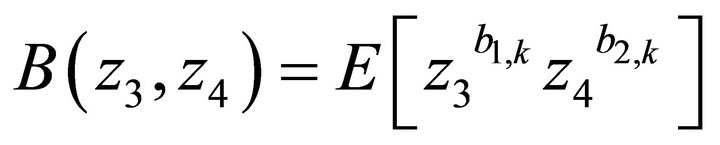 , independent of k. We define the marginal pgfs of the exogenous arrivals to PQS 2 from class-1 and class-2 customers during a slot by
, independent of k. We define the marginal pgfs of the exogenous arrivals to PQS 2 from class-1 and class-2 customers during a slot by 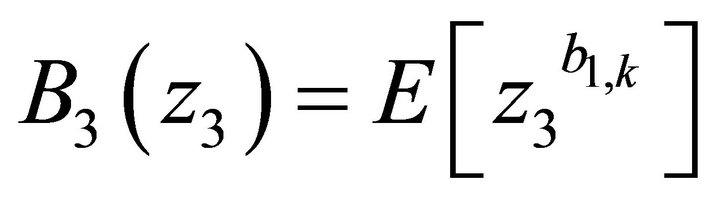 and
and  respectively.
respectively.
The marginal exogenous arrival rates of class-j (j = 1, 2) to PQS 2 are denoted by . We further denote the total number of exogenous arrivals to PQS 2 during slot k by
. We further denote the total number of exogenous arrivals to PQS 2 during slot k by , with corresponding pgf
, with corresponding pgf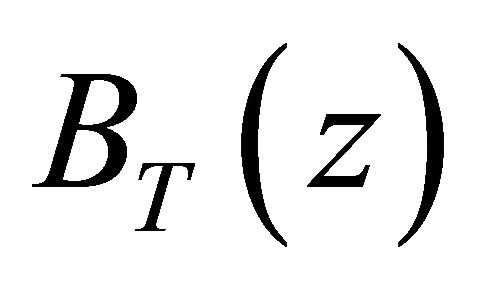 . The total arrival rate to PQS 2 is denoted by
. The total arrival rate to PQS 2 is denoted by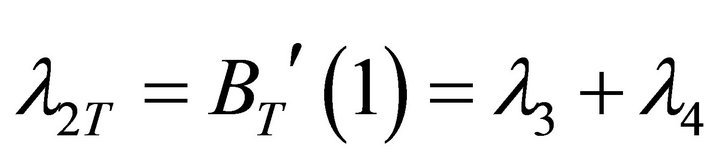 . The total arrival rate to the whole system is denoted by
. The total arrival rate to the whole system is denoted by
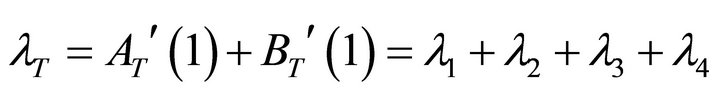 .
.
In the sequel, we assume that the system is stable and that a stochastic equilibrium exists.
Our model allows for the number of class-1 and class-2 arrivals to each PQS, within a slot, to be correlated random variables. This type of correlation can occur for instance when an incoming job (customer) can be split into two parts, an urgent and a non-urgent part, where the urgent part is of class-1, while the non-urgent part is of class-2. Taking into account this correlation in the arrival process leads to more accurate performance results [10]. In the next sections, we will demonstrate that an analysis based on probability generating functions approach can be used to derive some relevant performance measures for the queuing system under consideration.
3. Mathematical Model
The queuing model, shown in Figure 1, can be formulated as a discrete-time multidimensional Markov chain. The state of the system is defined by 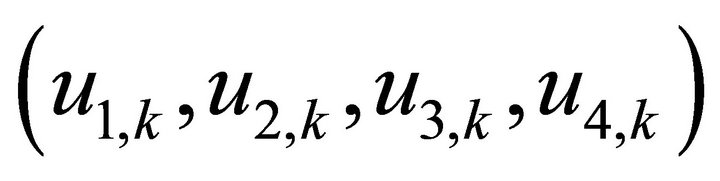 where
where  is the system content of node i (i = 1 4) at the end of the kth slot. The evolution of the system contents is described by the following system equations:
is the system content of node i (i = 1 4) at the end of the kth slot. The evolution of the system contents is described by the following system equations:
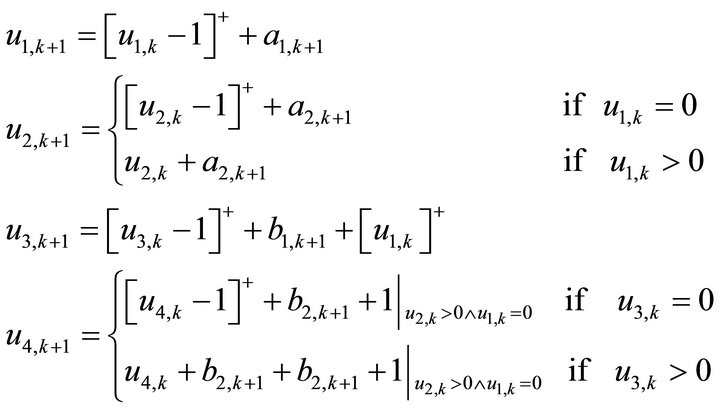 (1)
(1)
where 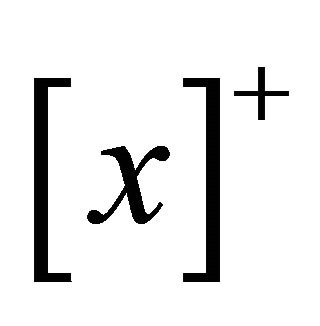 is a binary-valued random variable which takes the value 1 if x > 0 and 0 otherwise, while
is a binary-valued random variable which takes the value 1 if x > 0 and 0 otherwise, while  is the indicator function which takes the value 1 if x is true and 0 otherwise.
is the indicator function which takes the value 1 if x is true and 0 otherwise.
The first two expressions in (1) follow from the fact that high priority customers are not in influenced by low-priority customers, while a low priority customer can only be served, if there are no high priority customers in PQS1 (which leads to the second equation). The last two expressions in (1) follow from similar arguments, in addition to taking into account the fact that the output of high/low priority queue in PQS1 (if any) will also constitute an input to the high/low priority queue in PQS2. We also took into account the fact that the lowpriority node (2) can only forward a customer to the downstream low-priority node (3) if it is not empty and if the there are no high priority customers in PQS1.
Next, define the JPGF of system contents at the end of the kth slot as follows:
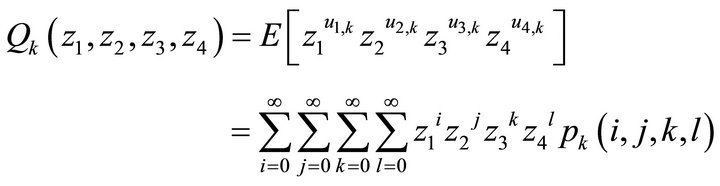 (2)
(2)
where
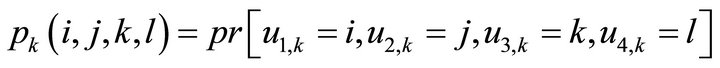
is the joint distribution of the system state vector at the end of the kth slot.
It follows that:
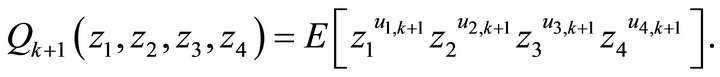
Taking the z-transform of the system Equations (1), and by considering the nine cases depicted in Figure 2, we derive, by means of some standard z-transform manipulations, the following relationship between
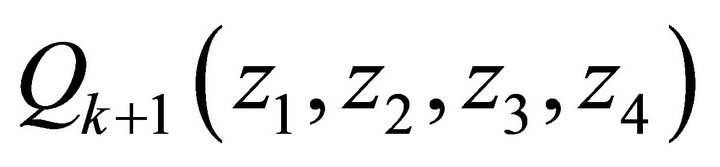 and
and ,
,
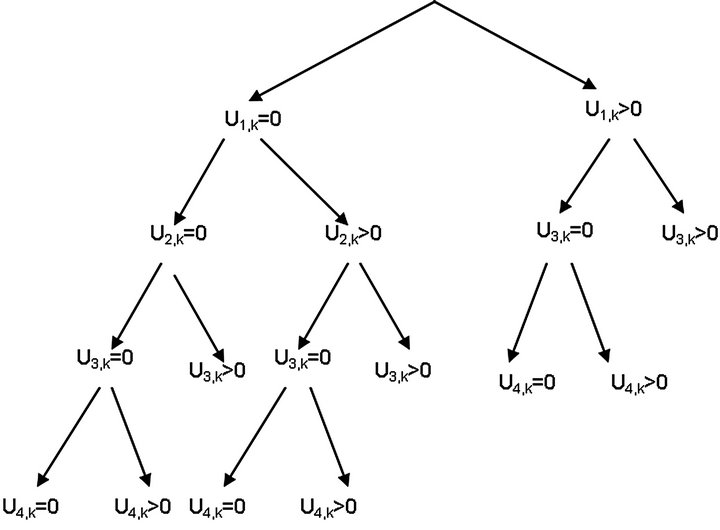
Figure 2. The nine cases used in the derivation of Equation (3).
as illustrated in Equation (3) (below).
Next, we define the steady-state JPGF of the system contents:

Applying the above limit to Equation (3) yields (see Equation (4) below):
Although it was not possible to determine all the seven boundary functions appearing in (4), as one of the 2 unknown boundary terms (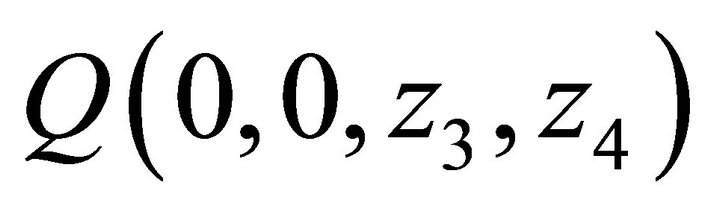 or
or ) could not be determined, we were able to derive the relevant performance measures related to mean system contents at each node and mean delays. It should be noted that the strong coupling between node 4 and the remaining nodes made the direct application of standard pgf techniques to extract all the boundary terms, appearing in (4), an intricate task.
) could not be determined, we were able to derive the relevant performance measures related to mean system contents at each node and mean delays. It should be noted that the strong coupling between node 4 and the remaining nodes made the direct application of standard pgf techniques to extract all the boundary terms, appearing in (4), an intricate task.
4. Determination of Relevant Boundary Terms
In this section, we show how to progressively determine some unknown boundary terms in order to extract relevant performance measures for the queuing model under consideration.
4.1. Determination of Q (z1, z2, 0, 0), Q (0, z2, 0, 0) and Q (0,0,0,0)
First, to determine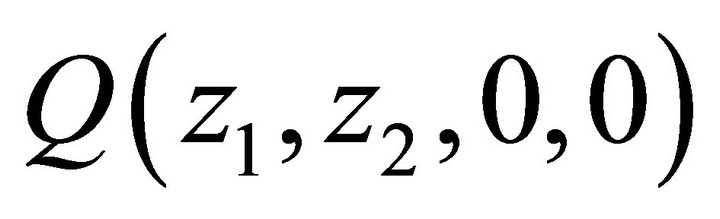 , let
, let 
and then  in Equation (3). Then:
in Equation (3). Then:
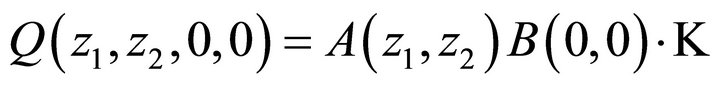 (5)
(5)
where:
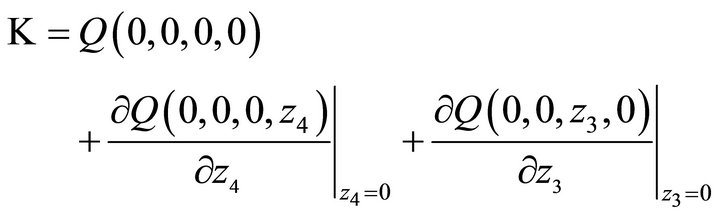 (6)
(6)
Next, to determine the constant , we set z1=z2=1 in Equation (5), which yields:
, we set z1=z2=1 in Equation (5), which yields:
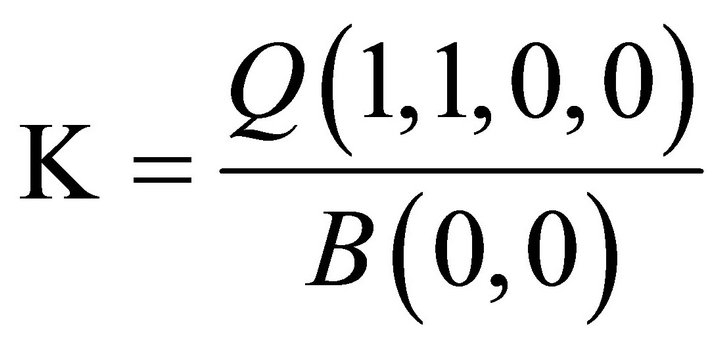 (7)
(7)
The boundary constant Q (1,1,0,0) is readily obtained from the normalization condition Q (1,1,1,1) = 1. In fact by setting 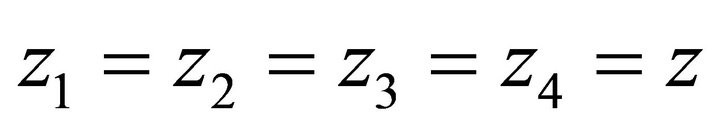 in Equation (4), it is easy to derive the following expression for the PGF of the total system content:
in Equation (4), it is easy to derive the following expression for the PGF of the total system content:
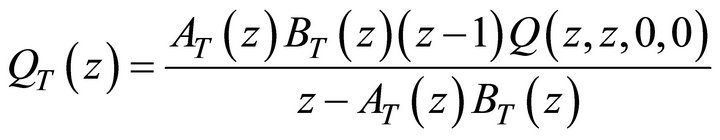 (8)
(8)
The normalization condition 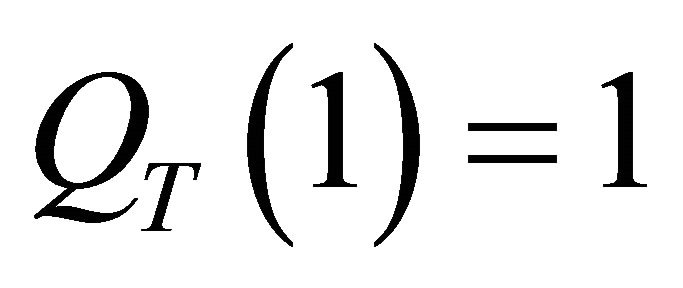 leads to
leads to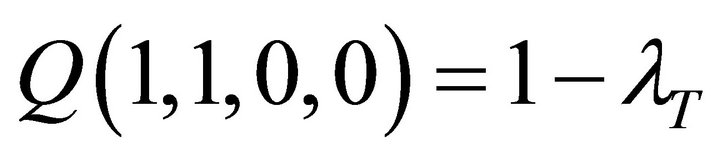 . By substituting this result back into Equation (7) and then into Equation (5), we immediately obtain the first unknown boundary function:
. By substituting this result back into Equation (7) and then into Equation (5), we immediately obtain the first unknown boundary function:
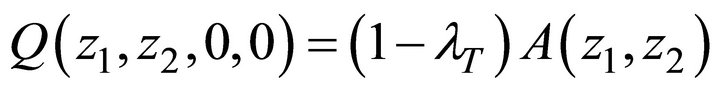 (9)
(9)
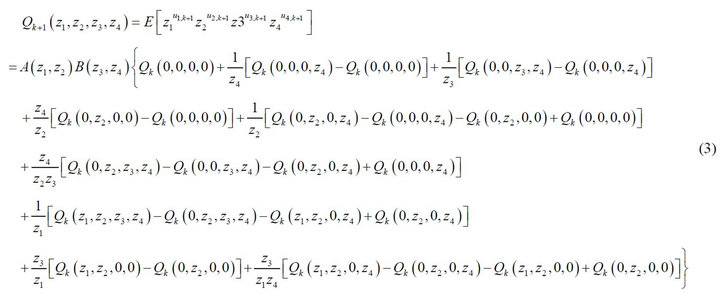

The other two related boundary terms are readily derived from Equation (9):
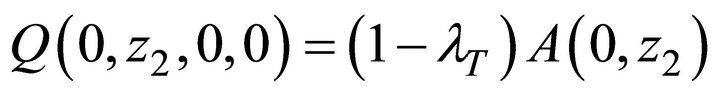 (10)
(10)
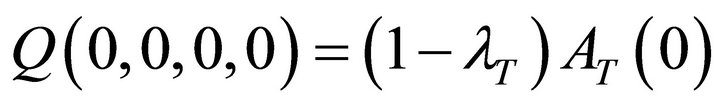 (11)
(11)
and therefore for the system to be stable, we require that  or equivalently,
or equivalently,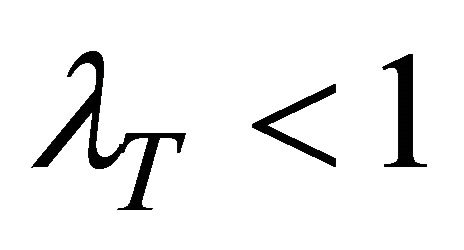 .
.
4.2. Relationship between Q (z1, z2, 0, z4) and Q (0, z2, 0, z4)
In this subsection, we determine 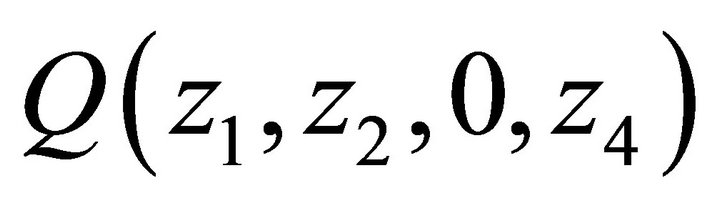 up to the boundary term
up to the boundary term . For this purpose, let
. For this purpose, let  and
and 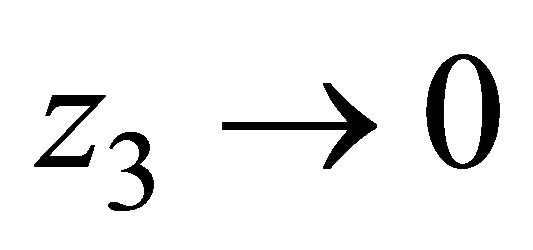 in Equation (3). Then:
in Equation (3). Then:
 (12)
(12)
where:
is independent of z1. Substituting z1 = 0 in Equation (12), we get:

and therefore:
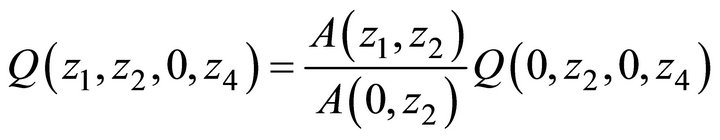 (13)
(13)
Thus 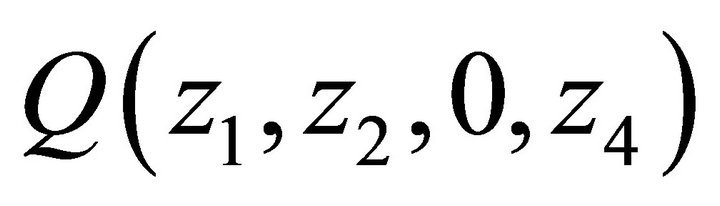 is determined up to the boundary term
is determined up to the boundary term .
.
4.3. Determination of Q (0, 0, z, z) and Q (0, z, 0, z)
To determine the boundary term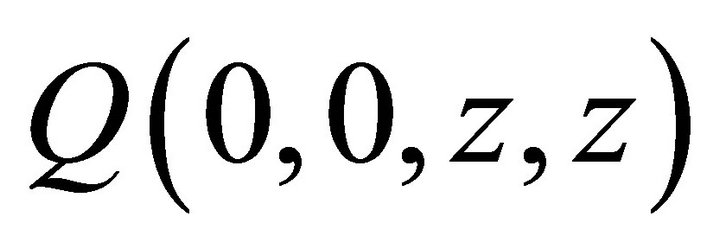 , we proceed as follows:
, we proceed as follows:
First by setting z1 = z2 = x and z3 = z4 = z in Equation (4), we obtain (see Equation (14) below):
From (9), we note that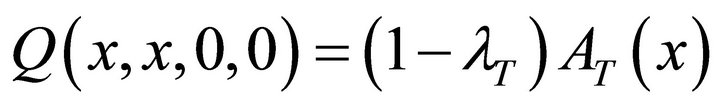 . Also since
. Also since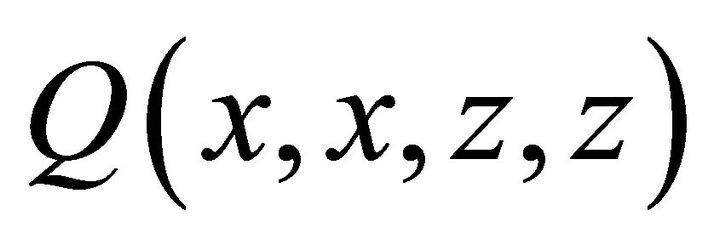 is analytic inside the polydisk (
is analytic inside the polydisk (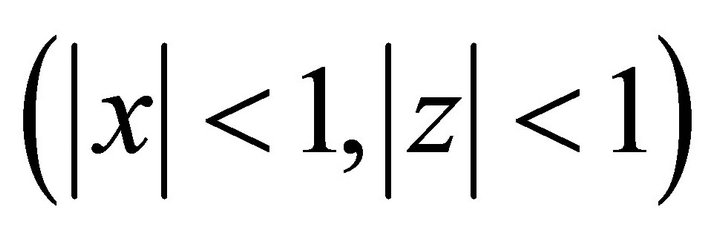 ), then the numerator must be zero whenever the denominator is zero. It follows that:
), then the numerator must be zero whenever the denominator is zero. It follows that:
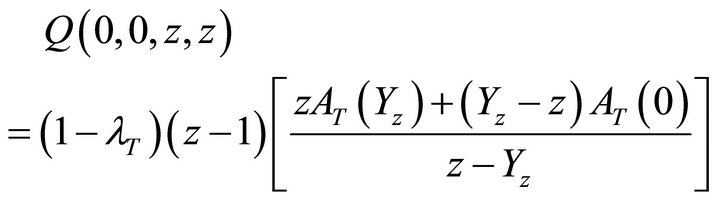 (15)
(15)
where 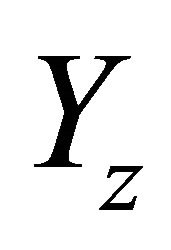 is the unique solution for x in the unit disk
is the unique solution for x in the unit disk 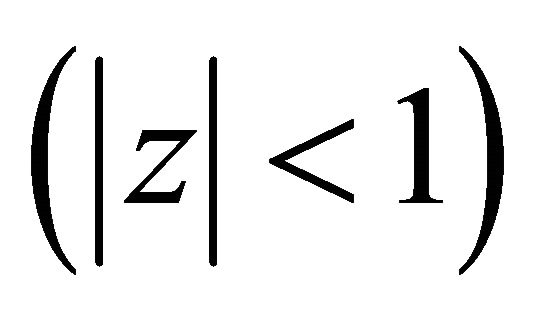 of the equation
of the equation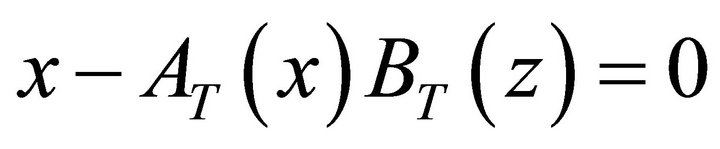 .
.
Next, we determine 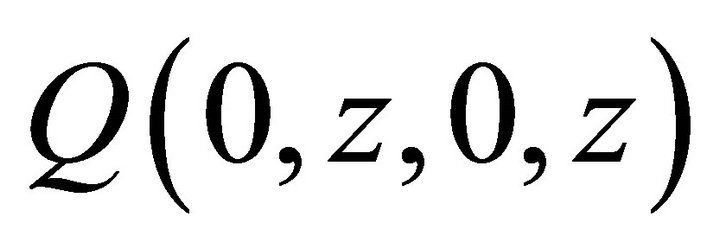 by proceedings as follows:
by proceedings as follows:
First by setting z1 = z3 = x and z2 = z4 = z in Equation (4), we obtain (see Equation (16) below):
From (9), we note that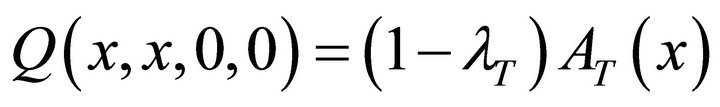 . Also from (13):
. Also from (13):
 (17)
(17)
Substituting for  and
and 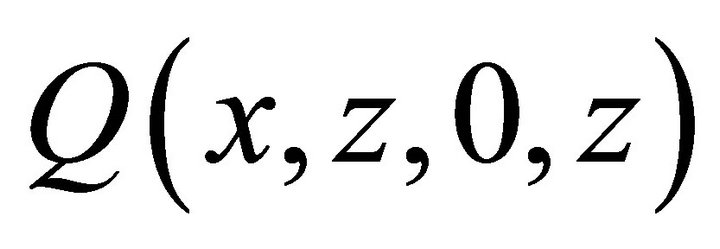 in (16) and since
in (16) and since 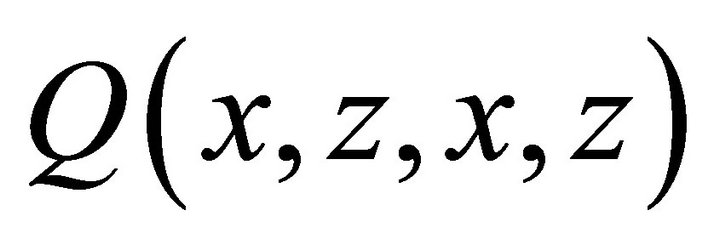 is analytic inside the polydisk
is analytic inside the polydisk , then from Rouche’s theorem, we get:
, then from Rouche’s theorem, we get:
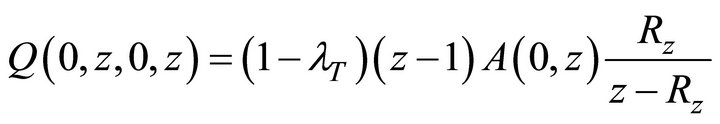 (18)
(18)
where 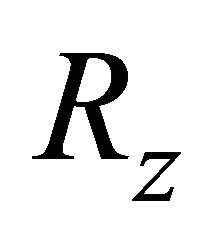 is the unique solution for x of the equation
is the unique solution for x of the equation 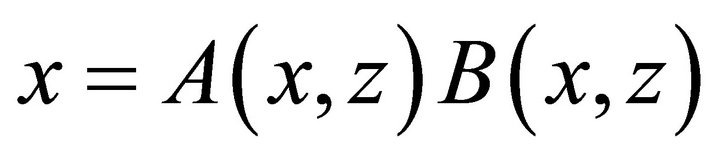 in the unit circle
in the unit circle .
.
5. Joint and Marginal PGFs
Having determined some relevant boundary terms, we can now easily derive the marginal PGFs of the system contents at nodes 1, 2, and 3, as well as several other JPGFs. This is illustrated below.
5.1. Joint and Marginal PGFs of High-Priority (Class-1) System Contents
Let 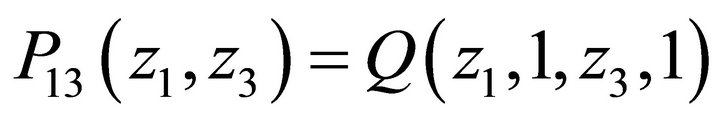 denote the JPGF of the
denote the JPGF of the
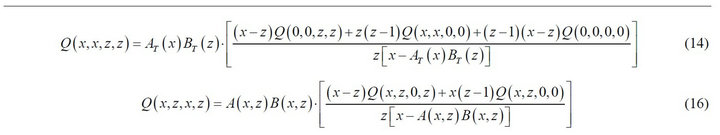
system contents of the high-priority queues at nodes 1 and 3. By setting z2 = z4 = 1 in Equation (4), we get (see Equation (19) below):
To determine the boundary terms 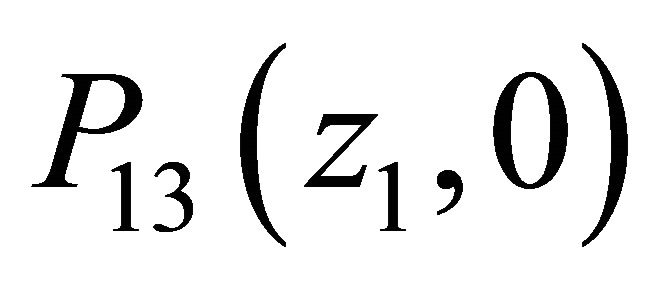 and
and 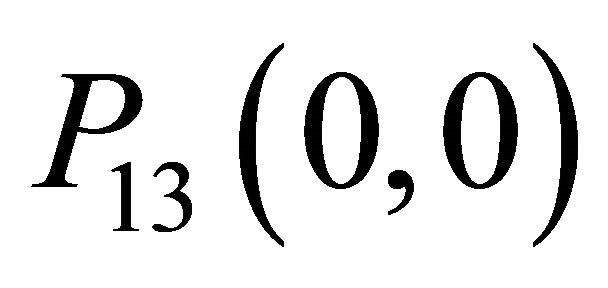 , appearing in (19), we first set z2 = z4 = 1 in (13):
, appearing in (19), we first set z2 = z4 = 1 in (13):
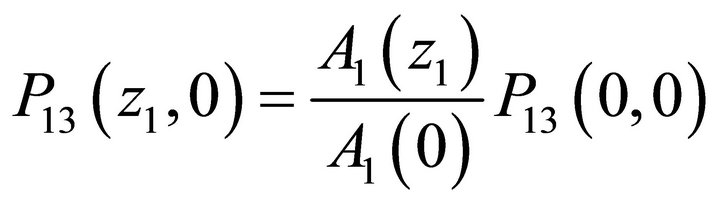 (20)
(20)
Next, from (19), the normalization condition P13 (1, 1) = 1 yields . Therefore setting
. Therefore setting  in (20), we get:
in (20), we get:
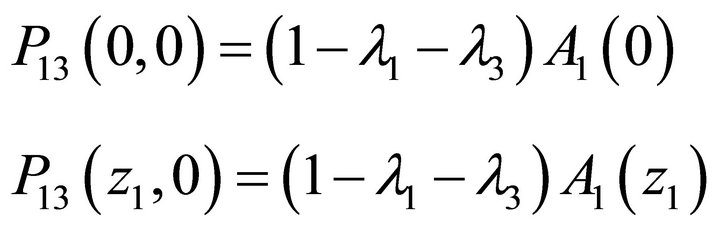 (21)
(21)
The remaining boundary term 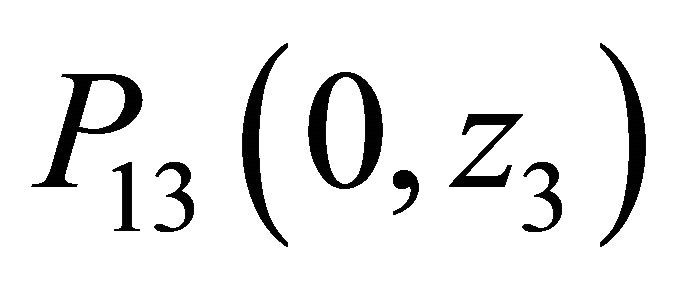 is readily obtained by substituting (20) and (21) into (19) and by invoking the analytical property of
is readily obtained by substituting (20) and (21) into (19) and by invoking the analytical property of 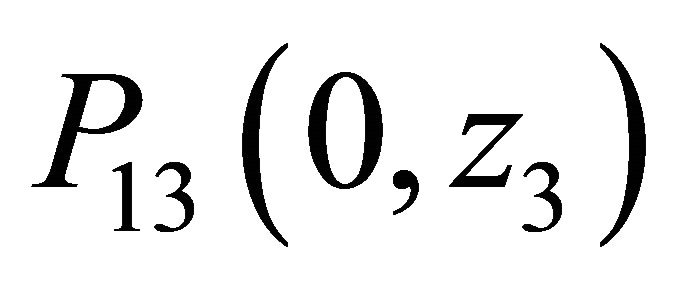 inside the polydisk
inside the polydisk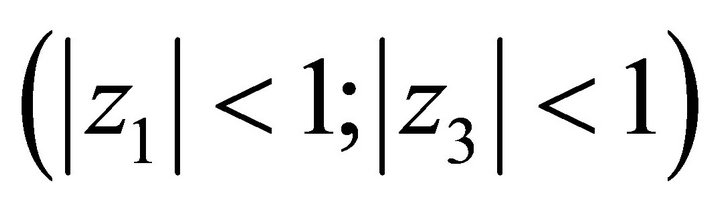 . It follows from Rouche’s theorem that:
. It follows from Rouche’s theorem that:
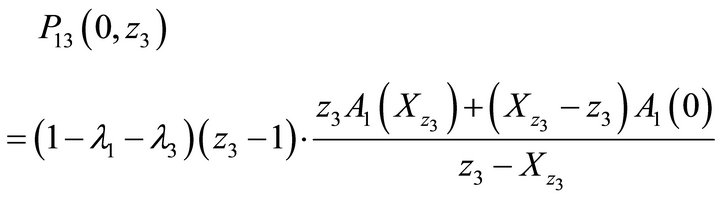 (22)
(22)
where for a given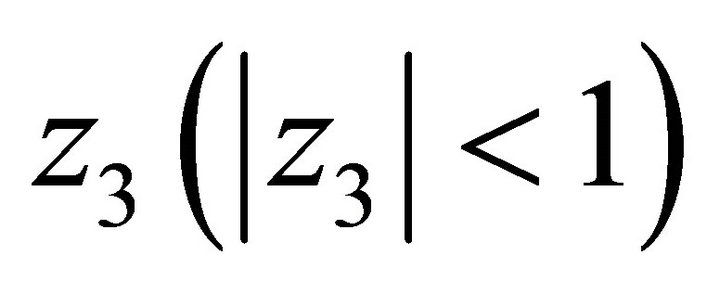 ,
, 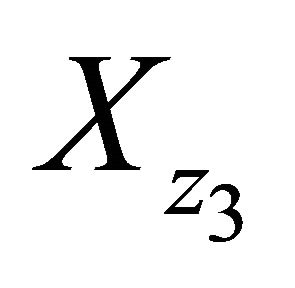 is the unique solution for z1 of the equation
is the unique solution for z1 of the equation 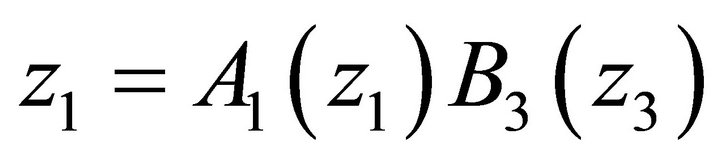 in the unit circle
in the unit circle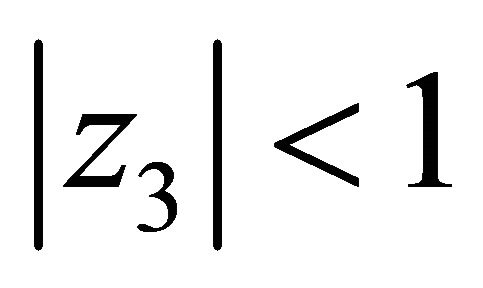 .
.
Substituting (21) and (22) back into (19), we obtain after few algebraic manipulations:
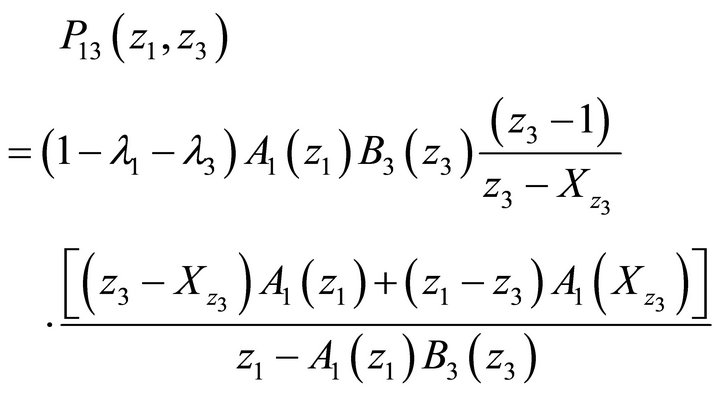 (23)
(23)
From the above, we can obtain expressions for the following:
● Marginal PGF of the number of class-1 customers in queue 1:
 (24)
(24)
● Marginal PGF of the number of class-1 customers in queue 3:
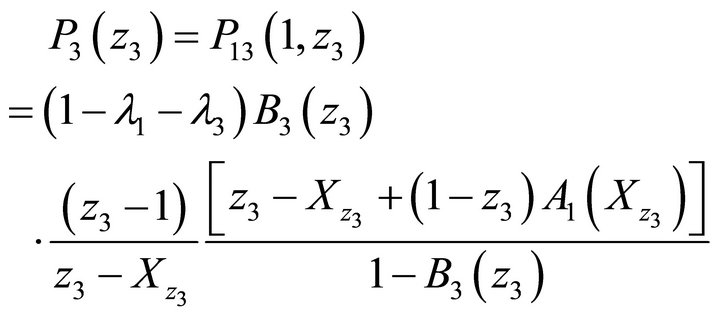 (25)
(25)
● PGF of the total number of class-1 customers in the system:
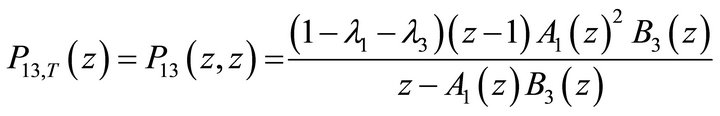 (26)
(26)
It should be noted that since the high-priority traffic (traversing nodes 1 and 3) is not influenced by the low-priority traffic (traversing nodes 2 and 4), then the above results for the JPGF  could have been derived by analyzing the performance of the two tandem queues 1 and 3, independently from the rest of the system. We carried this analysis and confirmed that the resulting JPGF of the system contents matches the one derived in Equation (23).
could have been derived by analyzing the performance of the two tandem queues 1 and 3, independently from the rest of the system. We carried this analysis and confirmed that the resulting JPGF of the system contents matches the one derived in Equation (23).
5.2. Joint PGFs of the System Contents in PQS1
Let  denote the JPGF of the system contents of the first priority queuing system(PQS 1). Then from Equation (4):
denote the JPGF of the system contents of the first priority queuing system(PQS 1). Then from Equation (4):
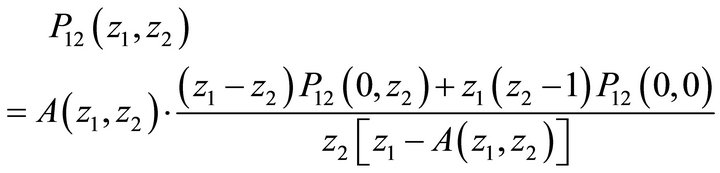 (27)
(27)
The boundary constant 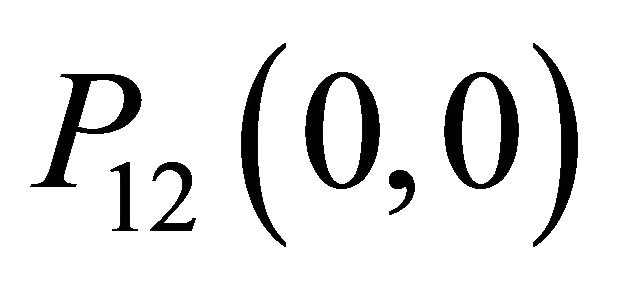 is readily obtained from the normalization condition
is readily obtained from the normalization condition , yielding
, yielding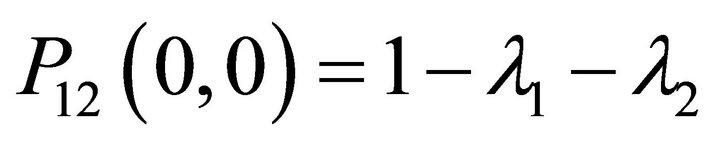 . The boundary term
. The boundary term 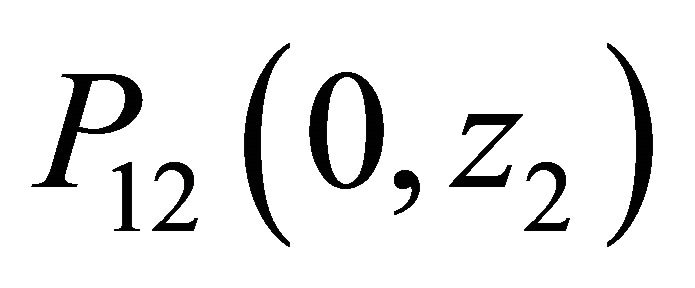 is readily obtained from (27) by applying Rouche’s theorem:
is readily obtained from (27) by applying Rouche’s theorem:
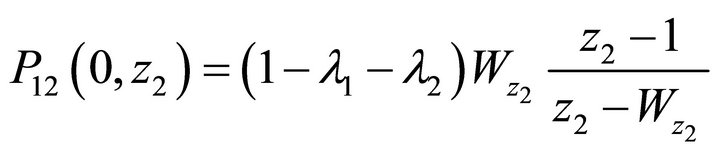 (28)
(28)
where for a given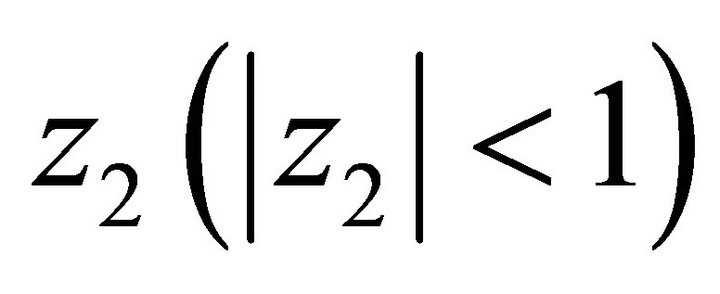 ,
, 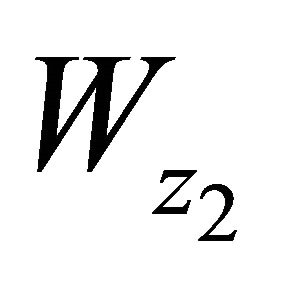 is the unique solution for z1 of the equation
is the unique solution for z1 of the equation 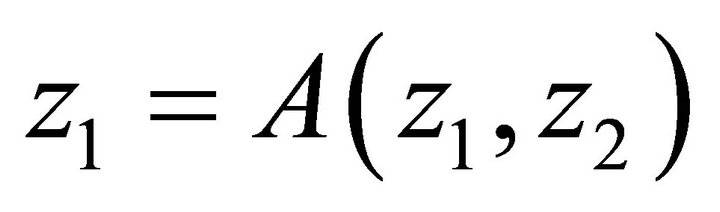 in the unit circle
in the unit circle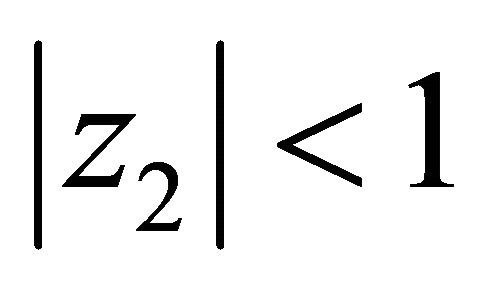 .
.
Next, by substituting for  and
and 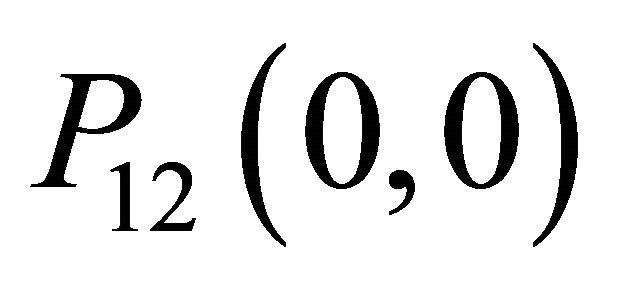 back into (27), we get:
back into (27), we get:
 (29)
(29)
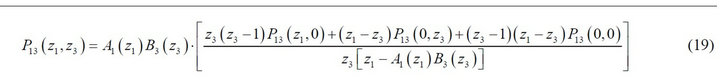
From the above, we can obtain expressions for the following:
● Marginal PGF of the number of class-1 customers in queue 1:
 (30)
(30)
● Marginal PGF of the number of class-2 customers in queue 2:
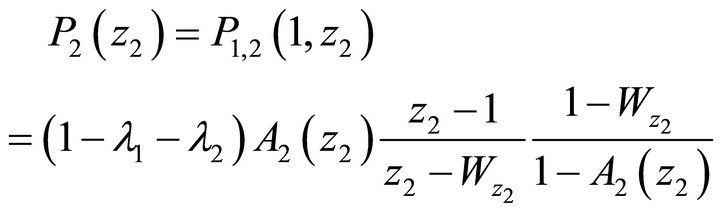 (31)
(31)
● PGF of the total number of class-1 customers in PQS1
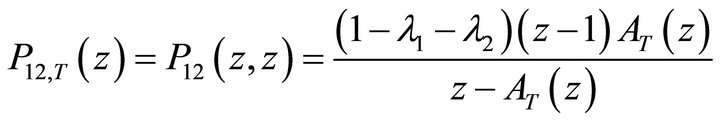 (32)
(32)
We also observe that the JPGF of the system contents of PQS 1 could have also been be derived by considering PQS 1 as an isolated priority queuing system. Such an analysis of a single stage PQS has been presented in [5] and our expressions (31-32) match those derived therein.
5.3. PGFs of Total Number of Customers in PQS2
Let 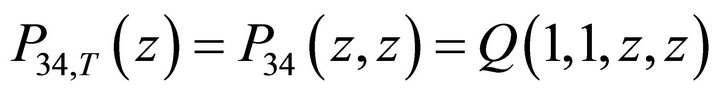 denote the JPGF of the total number if customers in the second priority queuing system (PQS 2). Then from (4):
denote the JPGF of the total number if customers in the second priority queuing system (PQS 2). Then from (4):
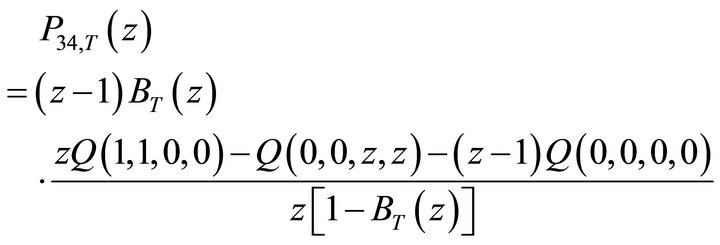 (33)
(33)
Using (9), (11) and (15), we can determine the unknown boundary terms appearing in the above equation, yielding:
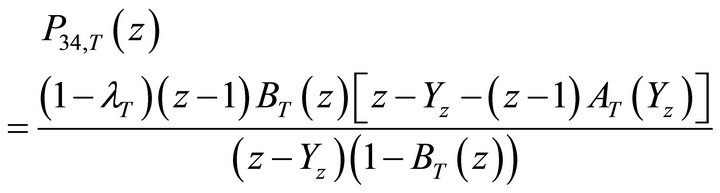 (34)
(34)
where, as defined earlier, for a given , Yz is the unique solution for x of the equation
, Yz is the unique solution for x of the equation  in the unit circle
in the unit circle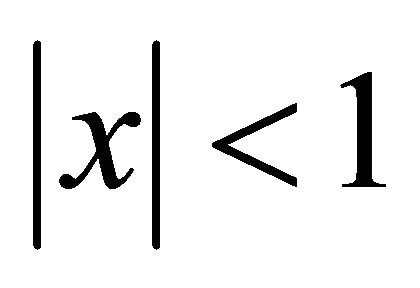 .
.
5.4. PGF of the Total Number of Class-2 Customers in the System
Let  denote the PGF of the total number of class-2 customers in the system. Then from Equation (4):
denote the PGF of the total number of class-2 customers in the system. Then from Equation (4):
 (35)
(35)
The unknown boundary term 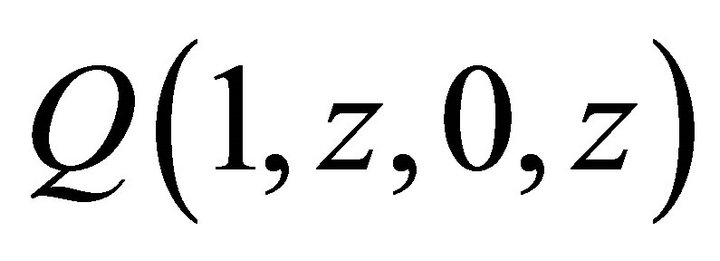 can be determined from (13) and (18), which yields:
can be determined from (13) and (18), which yields:
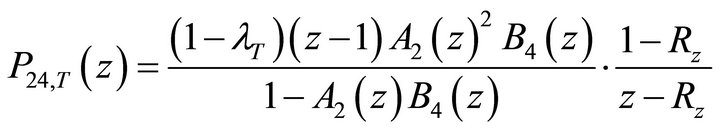 (36)
(36)
where  is the unique solution for x of the equation
is the unique solution for x of the equation 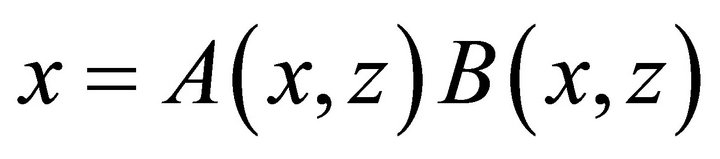 inside the unit circle
inside the unit circle .
.
5.5. PGF of the Total System Contents
Let 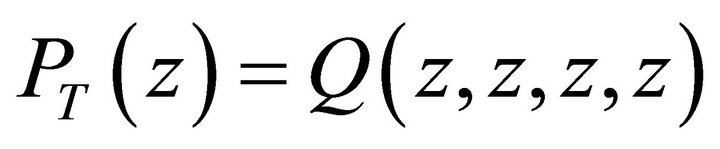 denote the PGF of the total system contents. Then using (4) and (9) we get:
denote the PGF of the total system contents. Then using (4) and (9) we get:
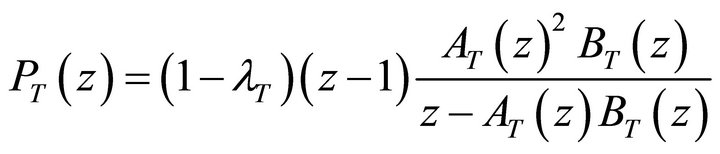 (37)
(37)
6. Calculation of the Moments
To compute the various moments of system contents, we introduce and recall the following notations:
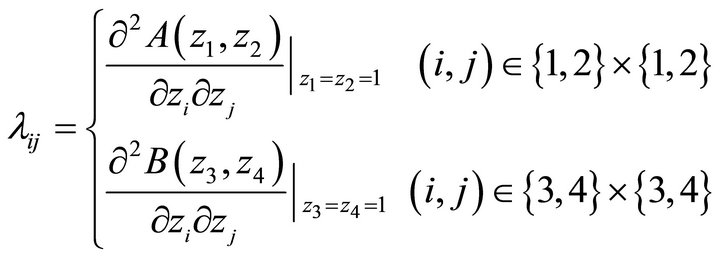

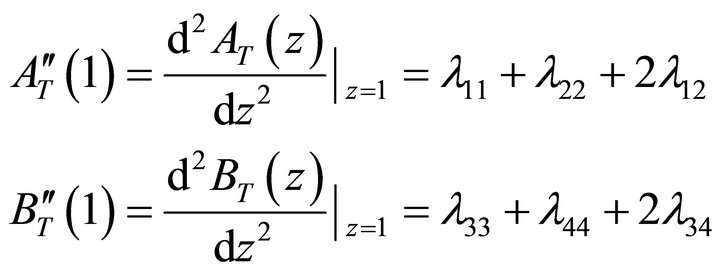 (38)
(38)
Next, we observe that the functions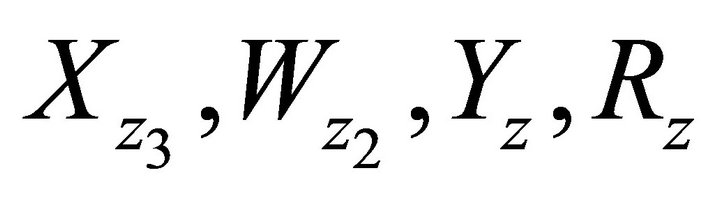 , appearing in the various pgfs of the system contents, can only be explicitly defined under simple arrival processes. Fortunately, the derivation of the first and higher moments of the system contents involves evaluating these functions and their first and higher order derivatives at
, appearing in the various pgfs of the system contents, can only be explicitly defined under simple arrival processes. Fortunately, the derivation of the first and higher moments of the system contents involves evaluating these functions and their first and higher order derivatives at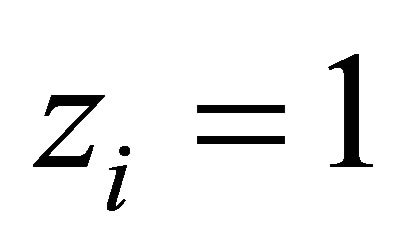 . These can be readily computed in closed-form.
. These can be readily computed in closed-form.
From the corresponding pgfs (24 - 26, 30 - 32, and 34, 36 - 37), the mean system content of class-j customers (j = 1, 2) and the mean total system contents are readily obtained:
● Mean system content of class-1 customers at node 1:
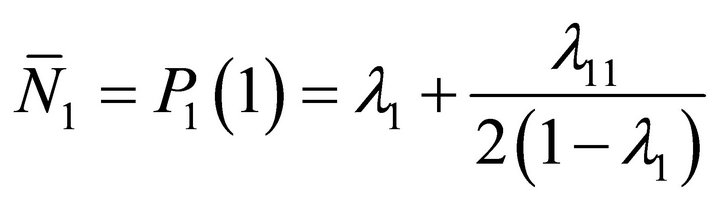 (39)
(39)
● Mean system content of class-1 customers at node 3:
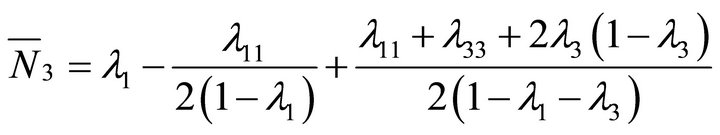 (40)
(40)
● Total mean system contents of class-1 customers:
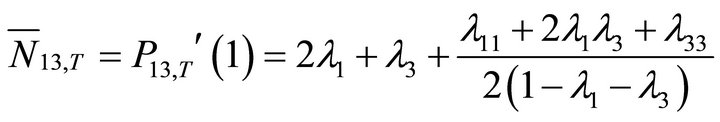 (41)
(41)
● Mean system content of class-2 customers at node 2:
 (42)
(42)
● Total mean system contents of class-2 customers:
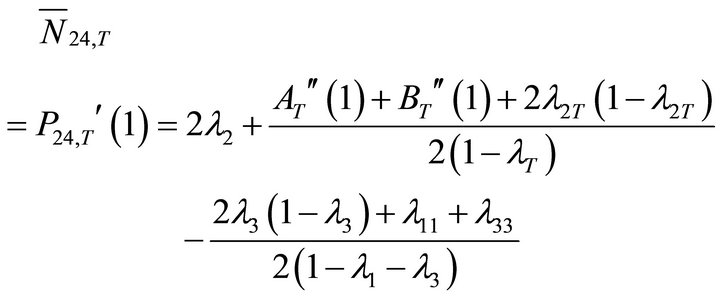 (43)
(43)
● Mean system content of class-2 customers at node 4:
The mean number of class-2 customers at node 4 can be derived by subtracting the mean system content of class-2 customers at node 2 from the total mean system contents of class-2 customer. Hence, using (42) and (43), we get:
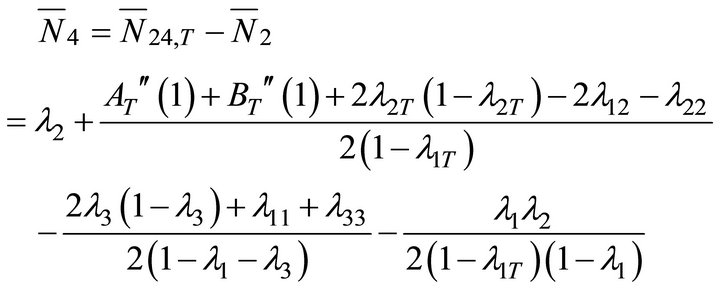 (44)
(44)
● Total mean system contents at PQS1:
 (45)
(45)
● Total mean system content at PQS2:
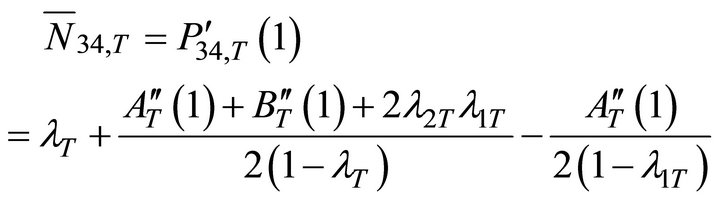 (46)
(46)
● Total mean system content
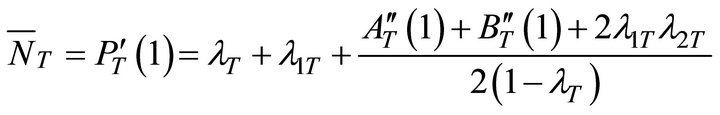 (47)
(47)
It can be easily verified that Equations (39-47) satisfy the expected results:
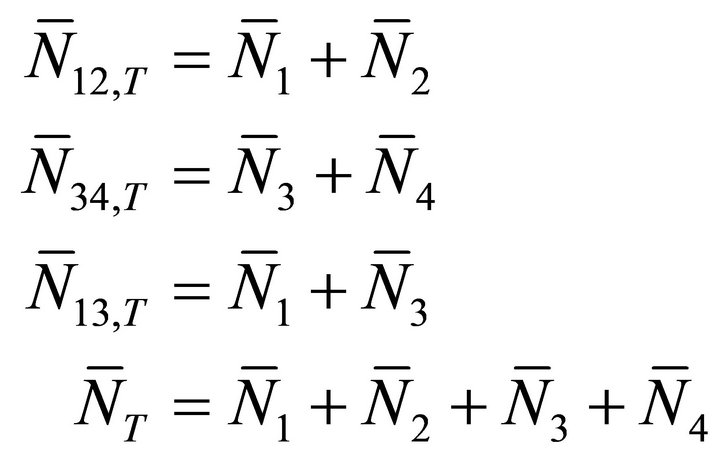 (48)
(48)
By using Little’s law, the following mean customer delays are readily obtained:
● Mean delay at each node:
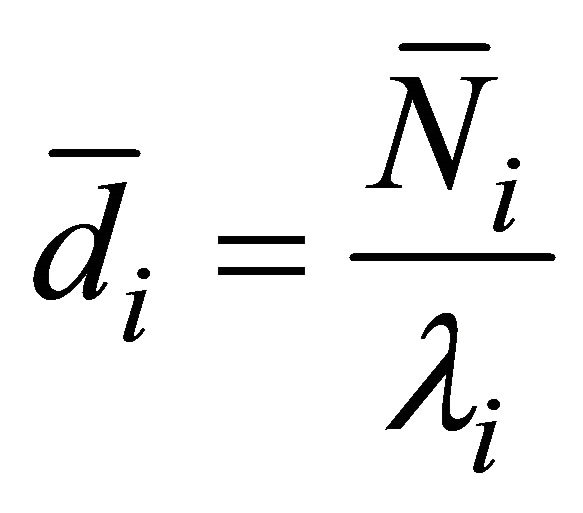 (49)
(49)
● Mean delay  of an arbitrary class-j customer (j = 1, 2):
of an arbitrary class-j customer (j = 1, 2):
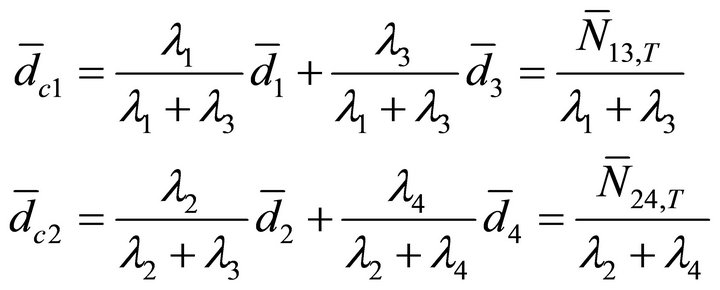 (50)
(50)
● Total average delay 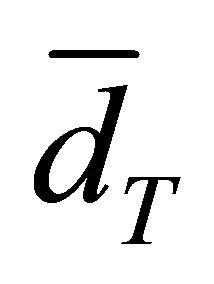 in the system:
in the system:
 (51)
(51)
7. Numerical Examples and Discussions
In this section, we illustrate our approach through some numerical examples. In particular, we will further probe into the influence of HOL priority on the performance of low-priority traffic stream. For this purpose, we consider two-dimensional Binomial exogenous arrival processes with JPGFs:
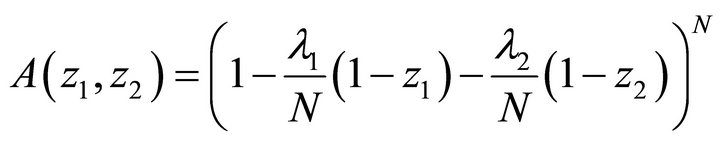

Further, we define 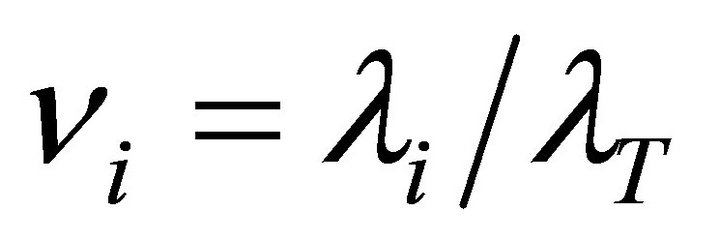 (i = 1, 2, 3) as the fraction of arrivals to node i among the total arrivals. For the numerical calculations, we have set N = 16 and
(i = 1, 2, 3) as the fraction of arrivals to node i among the total arrivals. For the numerical calculations, we have set N = 16 and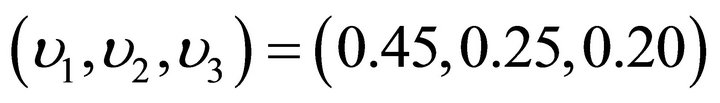 .
.
In Figure 3, the mean customer delay at each node as well as the total average delay, are plotted as a function of the total arrival rate . The mean delay
. The mean delay  at each node and the total average delay
at each node and the total average delay 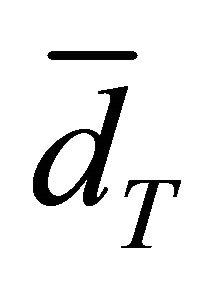 were computed by substituting for
were computed by substituting for  as given in Equations (39), (40), (42), and (44) into (49) and (51), respectively.
as given in Equations (39), (40), (42), and (44) into (49) and (51), respectively.
Figure 4 shows the mean delay of an arbitrary class-j
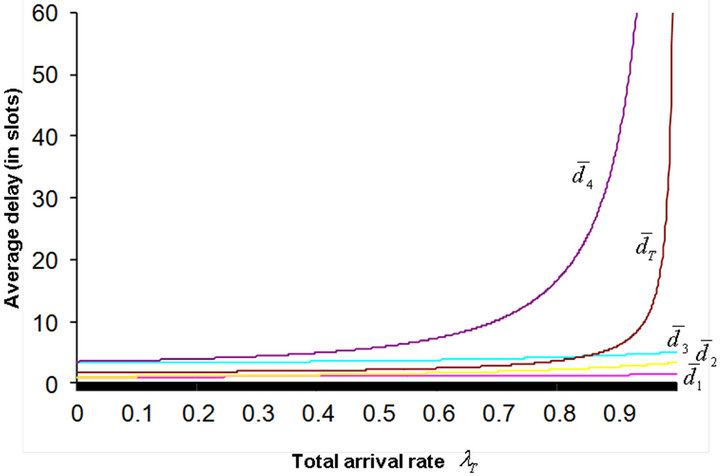
Figure 3. Mean delays versus total arrival rate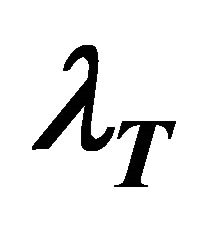 .
.
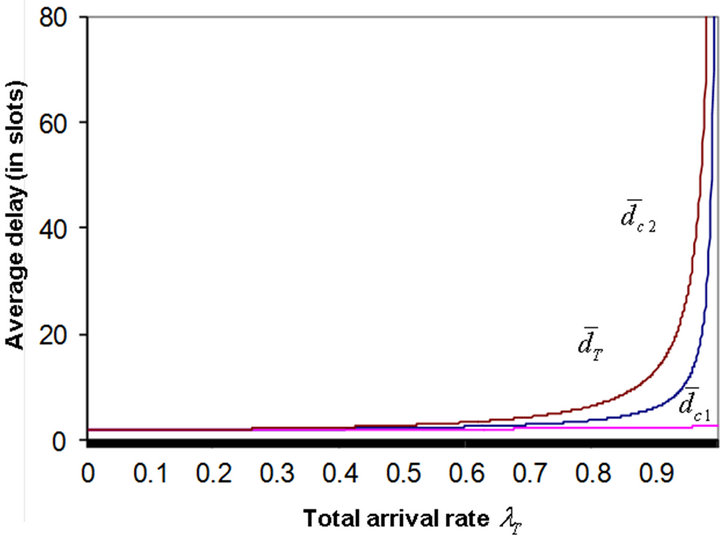
Figure 4. Mean delay of a class-j customer (j = 1, 2).
customer (j = 1, 2) and the total average delay as a function of the total arrival rate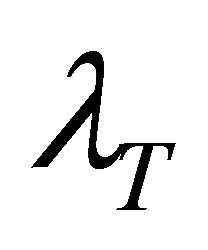 . In this case, the mean delay
. In this case, the mean delay  for each class j customer was computed by substituting for
for each class j customer was computed by substituting for  and
and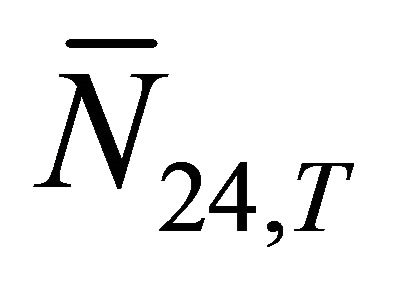 , as given in Equations (41) and (43), into (50).
, as given in Equations (41) and (43), into (50).
As may be seen from the above figures, the HOL priority scheduling has a significant influence on the mean delay of the low-priority (class-2) customers. This starvation effect is even more significant at node 4. To this regards, recall that class-2 customers arriving at the access node (2) are subjected to two consecutive HOL interruption processes due to the potential presence of higher priority customers at nodes 1 and 3. The above results not only echo but also amplify previous concerns related to the unfairness of the static HOL priority scheduling mechanism for low-priority traffic. Therefore HOL scheduling should be used with caution.
Our research also suggests that more research is needed to come-up with efficient priority mechanisms that exhibit better fairness and that can be easily implemented in real-time. Earlier contributions in this regards focused on a class of dynamic priority schemes that are based on the queue-length-threshold scheduling discipline. Under this scheme, the priority scheduling can dynamically change, based on the queue lengths (see for example [11-15]) [16]. Some More recent contributions include the work of Maertens et al. [17-19] on priority jumping mechanisms and the contribution of De Vuyst et al. [20,21] on reservation-based priority disciplines.
8. Conclusions and Future Research
In this paper, we presented an exact analysis of a two HOL priority queuing systems in a tandem configuration. For each PQS, our model allows for possible correlation between the numbers of arrivals of the two classes of customers during a slot. We showed how a generating function approach can be used to derive closed-form expressions for several performance measures. Finally we have demonstrated, via numerical examples, the negative impact the HOL priority scheduling on performance of the low-priority traffic.
This work can be further explored in many directions. For instance, it would be interesting to derive expressions for the pgf of customer delay and characterize the endto-end delay of a tagged customer. The characterization of the asymptotic behavior of the tail distributions of the various system contents is still an open research issue.
Finally, our analysis can also be extended to handle the case where customers leaving the first PQS stage are allowed to leave the system with a pre-assigned probability. These are left for future research.
REFERENCES
- A. Khamisy and M. Sidi, “Discrete-Time Priority Queues with Two-State Markov Modulated Arrivals,” Stochastic Models, Vol. 8, No. 2, 1992, pp. 337-357. doi:10.1080/15326349208807228
- M. Sidiand and A. Segall, “Structured Priority Queuing Systems with Applications to Packet-Radio Networks,” Performance Evaluation, Vol. 3, No. 4, 1983, pp. 265- 275. doi:10.1016/0166-5316(83)90036-6
- T. Takine, B. Sengupta and T. Hasegawa, “An Analysis of a Discrete-Time Queue for Broadband ISDNwith Priorities among Traffic Classes,” IEEE Transactions on Communications, Vol. 42, No. 2-4, 1994, pp. 1837-1845. doi:10.1109/TCOMM.1994.582893
- T. Takine, “A NonpreemptivePriority MAP/G/1 Queue with Two Classes of Customers,” Journal of Operations Research Society of Japan, Vol. 39, No. 2, 1996, pp. 266- 290.
- J. Walraevens, B. Steyaertand H. Bruneel,” Performance Analysis of a Single-Server ATM Queue with a Priority Scheduling,” Computers and Operations Research, Vol. 30, No. 12, 2003, pp. 1807-1829. doi:10.1016/S0305-0548(02)00108-9
- J. Walraevens, D. Fiems and H. Bruneel, “Transient Analysis of a Discrete-Time Priority Queue,” Proceedings of the 12th International Conference on Analytical and Stochastic Modelling Techniques and Applications (ASMTA 2005), Riga, June 2005, pp. 17-24.
- K. Laevens and H. Bruneel, “Discrete-Time Multiserver Queues with Priorities,” Performance Evaluation, Vol. 33, No. 4, 1998, pp. 249-275. doi:10.1016/S0166-5316(98)00024-8
- J. Walraevens, D. Fiems, S. Wittevrongel and H. Bruneel, “Calculation of Output Characteristics of a Priority Queue through a Busy Period Analysis,” European Journal of Operational Research, Vol. 198, No. 3, 2009, pp. 891-898. doi:10.1016/j.ejor.2008.11.018
- F. Kamoun, “Performance Analysis of a Non-Preemptive Priority Queuing System Subjected to a Correlated Markovian Interruption Process,” Computers and Operations Research, Vol. 35, No. 12, 2008, pp. 3969-3988. doi:10.1016/j.cor.2007.06.001
- J. Walraevens, D. Fiems and H. Bruneel, “The DiscreteTime Preemptive Repeat Identical Priority Queue,” Queuing Systems, Vol. 53, No. 4, 2006, pp. 231-243. doi:10.1007/s11134-006-7770-x
- R. Chipalkatti, J. F. Kurose and D. Towsley, “Scheduling Policies for Real-Time and Nonreal-Time Traffic Packet Switching Node,” Proceedings of the IEEE INFOCOM ’89, Ottawa, April 1998, pp. 774-783.
- B. I. Choi and Y. Lee, “Performance Analysis of a Dynamic Priority Queue for Traffic Control of Bursty Traffics in ATM Networks,” IEEE Proceedings of Communications, Vol. 148, No. 3, 2001, pp. 181-187. doi:10.1049/ip-com:20010115
- D. I. Choi, B. D. Choi and D. Sung, “Performance Analysis of Priority Leaky Bucket Scheme with QueueLength-Threshold Scheduling Policy,” IEEE Proceedings of Communications, Vol. 145, No. 6, 1998, pp. 395-401. doi:10.1049/ip-com:19982287
- C. Knessl, D. I. Choi and C. Trier, “A Dynamic Priority Queue Model for Simultaneous Service of Voice and Data Traffic,” SIAM Journal on Applied Mathematics, Vol. 63, No. 2, 2002, pp. 398-422. doi:10.1137/S0036139901390842
- J. T. Lee and Y. H. Kim, “Performance Analysis of a Hybrid Priority Control Scheme for Input and Output Queuing ATM Switches,” Proceedings of INFOCOM ’98, San Francisco, 29 March-2 April 1998, pp.1470-1477. doi:10.1109/INFCOM.1998.662965
- T. Maertens, J. Walraevens and H. Bruneel, “Performance Analysis of a Single-Server Queue with HOL-PJ Priority Scheduling Discipline,” Proceedings of the Second International Working Conference on Performance Modelling and Evaluation of Heterogeneous Networks (HETNETs ’04), Ilkley, 26-28 July 2004, pp. 1-10.
- T. Maertens, J. Walraevens and H. Bruneel, “On Priority Queues with Priority Jumps,” Performance Evaluation, Vol. 63, No. 12, 2006, pp. 1235-1252. doi:10.1016/j.peva.2005.12.003
- T. Maertens, J. Walraevens and H. Bruneel, “A Modified HOL Priority Scheduling Discipline: Performance Analysis,” European Journal of Operational Research, Vol. 180, No. 3, 2007, pp. 1168-1185. doi:10.1016/j.ejor.2006.05.004
- T. Maertens, J. Walraevens, M. Moeneclaey and H. Bruneel,” Performance Analysis of a Discrete-Time Queuing System with Priority Jumps,” International Journal of Electronics and Communications, Vol. 63, No. 10, 2009, pp. 853-858. doi:10.1016/j.aeue.2008.07.004
- S. De Vuyst, S. Wittevrongel, D. Fiems and H. Bruneel, “Controlling the Delay Trade-off Between Packet Flows UsingMultiple Reserved Places,” Performance Evaluation, Vol. 65, No. 6-7, 2008, pp. 484-511. doi:10.1016/j.peva.2007.12.008
- S. De Vuyst, D. Wittevrongel and H. Bruneel, “Place Reservation: Delay Analysis of a Novel Scheduling Mechanism,” Computers and Operations Research, Vol. 35, No. 8, 2008, pp. 2447-2462. doi:10.1016/j.cor.2006.12.003

