Received 11 July 2016; accepted 20 August 2016; published 23 August 2016

ABSTRACT

We prove that e + π is a transcendental number. We use proof by contradiction. The key to solve the problem is to establish a function that doesn’t satisfy the relational expression that we derive, thereby produce a conflicting result which can verify our assumption is incorrect.

Keywords:

Hilbert’s Conjecture, Transcendental Number, The Transcendence of e + π

Subject Areas: Algebra, Algebraic Geometry

1. Introduction

Hilbert’s seventh problem is about transcendental number. The proof of transcendental number is not very easy. We have proved the transcendence of “e” and “π”. However, for over a hundred years, no one can prove the transcendence of “e + π” [1] . The purpose of this article is to solve this problem and prove that e + π is a transcendental number.

2. Proof

1) Assuming 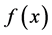is any one polynomial of degree n.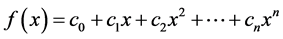, , 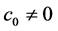Let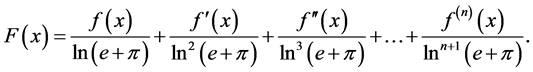

Now we consider this integral: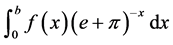. By integrability by parts, we can get the following For- mula 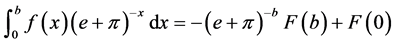(2.1):

(2.1)

2) Assuming 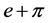is a algebraic number, so it should satisfy some one algebraic equation with integral coefficients:,.

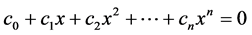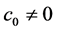According to Formula (2.1), using 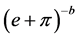multiplies both sides of Formula (2.1) and let be separately equal to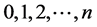. We get the following result.

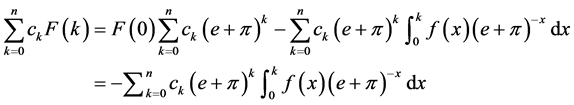(2.2)

So, all we need to do or the key to solve the problem is to find a suitable 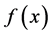that it doesn’t satisfy the Formula (2.2) above.

3) So we let 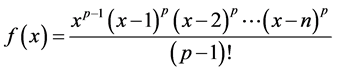[2] , , and b is a prime number Because of, , so can be divisible by and when, all of equal zero.

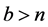Furthermore, we consider whose (p + a)-th derivative (); when, the derivative is zero. And when, the derivative is. What’s more, the coefficient of is a multiple of (p + a)!, so it’s alse a multiple of (p − 1)! and p.

By the analysis above, we can know that are multiples of p.

Now we see; we know,

and its the sum of the first p − 1 item is zero (because the degree of each term of is not lower than). All from the (p + 1)-th item to the end are multiples of p. But the p-th item is the (p − 1)-th derivative of. So, , and and are congruence, written. Thereby, , but, , and b is a prime number, so

, (2.3)

4) Next, we need to prove that when p tends to be sufficiently large.

When x changes from 0 to n, the absolute value of each factor of is not more than n, so,.

So by integral property: when,

Let M equal

thus,

When. So, (2.4)

Finally, according to (2.3) and (2.4), we know (2.2) is incorrect. So, e + π is a transcendental number.

3. Conjecture

By the proof above, we conclude that e + π is a transcendental number. Besides, I suppose is also a transcendental number. What’s more, when a and b are two real numbers, and, I suppose that is a transcendental number.

Acknowledgements

I am grateful to my friends and my classmates for supporting and encouraging me.

Cite this paper

Jiaming Zhu, (2016) The Proof of Hilbert’s Seventh Problem about Transcendence of e＋π. Open Access Library Journal,03,1-3. doi: 10.4236/oalib.1102893

References