Received 30 June 2016; accepted 16 August 2016; published 19 August 2016

ABSTRACT

This paper presents an enhanced model of geometric fractional Brownian motion where its volatility is assumed to be stochastic volatility model that obeys fractional Ornstein-Uhlenbeck process. The method of estimation for all parameters (α, β, m, μ, H₁, and H₂) in this model is derived. We calculated the value of European call option using the estimates based on the methods of Masnita [1] [2] and Kukush [3] , traditional Black-Scholes European option price, in addition to proposed model in order to make comparison study.

Keywords:

Geometric Fractional Brownian Motion, Fractional Ornstein-Uhlenbeck Process, Long Memory Stochastic Volatility, Innovation Algorithm, Constraint Transcription Method, Segmentation, Option Pricing, KLCI

Subject Areas: Financial Mathematics

1. Introduction

One of the most important models in financial world is a geometric Brownian motion (GBM) introduced by Samuelson in 1964 [4] . This model is widely used as the underlying process of a risky market. Extension of this model includes the added long memory properties named geometric fractional Brownian motion (GFBM). GFBM model includes important parameters that are used in fractional Black-Scholes model which is a natural improvement of standard Black-Scholes model widely used in options market.

Based on the literature, early works on GBM assumed volatility to be a constant. However this assumption is rejected by most empirical studies [5] - [8] which led to some market crashes such as Black-Monday in 1987, the Asian crisis in 1989 and housing bubble and credit crisis 2007-2009. Thus, GBM is later studied with the assumption that volatility is stochastic [9] - [14] . Moreover, researchers showed that time series data depending on this model exhibited the existence of memory (some trend-like behavior) which implied deducing the incorporation of the long memory parameter (H), thus leading to the introduction of geometric fractional Brownian motion (GFBM).

GFBM model includes important parameters that are normally used in fractional Black-Scholes model which is a natural improvement of standard Black-Scholes model, widely accessible in options market. However, there are few contributions in the literature that estimate these parameters. The expressions of parameters in this model are too involved; in particular in covariance and its inversion of the likelihood function, thus hinder works of estimation.

However, some ground works have been recently established. Kukushin [1] developed an incomplete maximum likelihood estimation approach for this model, where the Hurst index H (the long memory parameter) is estimated by some other heuristic methods, such as the variation analysis or R/S analysis. To extend further this work, complete maximum likelihood estimation (CMLE) method was introduced by Misiran et al. [1] and [2] that are able to simultaneously estimate all parameters involved in GFBM (μ, σ and H). However, in Misiran and Kukush’s works, the volatility is assumed constant for the simplicity of calculation. Such assumption was rejected by empirical studies as previously explained. Thus, in this article, we aim to extend the previous work by considering the stochastic volatility in the said model.

Stochastic volatility (SV) can be referred to the volatility and common dependence between variables that are permitted to fluctuate over time, instead of remain constant. The main idea in stochastic volatility is that asset returns are well approximated by mixture distribution. This mixture reflects the level of new arrivals activity of data in the financial market. These models are able to overcome weaknesses in Black-Choles model.

One of the most important continuous settings of stochastic volatility is the Ornstein-Uhlenbeck (OU) model, developed by Uhlenbeck and Ornstein in [15] . It is the analogue of the famous autoregressive moving average (ARMA) process in discrete time. The main property of this model is the mean-reverting property, i.e. the mean acts as an equilibrium level for the process. OU model is habitually applied to model exchange rates, stochastic volatility, and interest rate [16] - [20] . In this work, we replace constant volatility in GFBM model by stochastic volatility that obeys the fractional Ornstein-Uhlenbeck process to provide better accuracy in describing real market behavior.

This article follows the sequence. First, a brief background on the GFBM and stochastic volatility are introduced. Then, the model is derived and followed by the estimation method. The application study is conducted to compare the proposed method with other methods.

2. Model Derivation

We briefly introduce the derivation of the model as follows. For detail derivation, we refer readers to Appendix A. Let 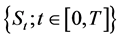represent the stock price process with the dynamic assumed by:

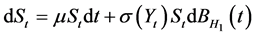(1)

where 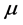is the mean of return, 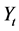is the stochastic process and 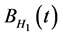is fractional Brownian motion with Hurst index, and 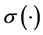is deterministic function. For simplicity of computations, in this work we choose 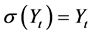as in [21] .

Let the dynamics of the volatility 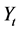be described by fractional Ornstein-Uhlenbeck (FOU) process which is the solution of the following stochastic differential equation:

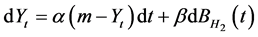(2)

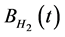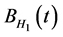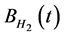where α, β and m are constant parameters that represent mean reverting of volatility, volatility of volatility, and mean of volatility, respectively. is another fractional Brownian motion. We assume that and are independent, and.

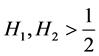We present the covariance functions involved in this derivation, as follows:

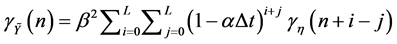(3)

(4)

(5)

(6)

3. Method of Estimation

To estimate the said parameters involved in (1) and (2), the likelihood function will be utilized. In general, likelihood functions for n random variables is given by:

(7)

By maximizing (7), we are able to get the efficient estimator of all the parameters. However, it is complicated to analytically maximizing such log likelihood function that is too involved, in particular the expression for the covariance function and its inversion. Alternatively, the innovation algorithm will be applied.

We use the definition of best linear prediction for stationary process from [22] as follows:

Definition: Given data the best linear predictor of for is and it can find by solving

(8)

where for.

(8) is called prediction equations, and are able to solve coefficients.

Suppose that is a stationary process and

(9)

By the definition of best linear predictors the coefficient satisfy

(10)

(A.10) can be written in matrix form as follows:

(11)

where is matrix, is an vector, and is an vector.

By (11), we get

(12)

Let, then

(13)

Thus,

(14)

Let

(15)

where, is an autoregressive parameter, and is standard deviation.

(15) can be written in matrix form as follows:

(16)

or

(17)

where and. Note that, where is the mean square error, given by

(18)

From (17), we have

(19)

So the autocovariance function is

(20)

and

(21)

The determinant is

(22)

The likelihood function is now transformed into the following optimization problem.

Problem P

Maximizes the cost function

where

(23)

subject to

(24)

(25)

From some calculations we obtained

(26)

and

(27)

The constraints in this optimization problem are too involved with covariance functions, so the optimization is difficult to solve. In order to simplify this problem, we use the constraint transcription method described in [23]

Maximizes the cost function:

(28)

subject to

(29)

where are the constraints in the original problem. Let this problem be referred to as Problem P. For each we approximate with, where

(30)

where some small number. We now append the approximate functions into the cost function to an appended cost function given below.

Problem P_ε,γ

(31)

where is a penalty parameter. This is an unconstraint optimization problem, which is referred to as Problem. For any given, there exists a such that for, the solution of Problem will satisfy the constraint of Problem P. Let be such a for each. Furthermore, the solution of Problem converges to the solution of Problem P.

4. Application to European Option Pricing

To determine the value of option, there are some factors to be taken into account, such as intrinsic value, time of expiration, volatility, interest rate and cash dividends paid. There are a number of option pricing models that use these parameters to control the fair market value of the option. The Black-Scholes model is the most widely used.

4.1. Classical Black-Scholes Model for European Option Pricing

Black-Scholes option pricing model constructed by Fischer Black and Myron Scholes in 1973. This model created for describing the market value of call option. Its formulated as:

(32)

Here, is the price of a call option, is the current stock price, K is the exercise price, r is the risk-free interest rate, and T is the time to maturity. and are the cumulative distribution function of the standard normal distribution.

(33)

and

(34)

where is the standard deviation of the stock price. In this model, the price is assumed to follow a geometric Brownian motion.

4.2. Fractional Black-Scholes Model for European Option Pricing

FBS model is the accepted improvement of BS model. The price at time of a European call option with the strike price K and maturity T is given by

(35)

where

(36)

and

(37)

where S is the underlying stock price at time t, r is the risk free interest rate, and is the cumulative function of a standard normal distribution [24] .

4.3. Data

Kuala Lumpur Composite Index (KLCI) is announced in 1986 in order to be a guideline of the actual performance indicator for the economy in general and especially for the overall Malaysia stock market. It includes of more than one-handed multi-sector companies from the Main Board in Bursa Malaysia which previously named as Kuala Lumpur Stock Exchange (KLSE).

We used a data set from KLCI which available online on http://www.econstats.com. The daily close price data set of KLCI from 3rd of January, 2005 to 29th of December, 2006 is studied; with total of observations of 494. The return series is then calculated in logarithm. The return is considered to avoid the high volatility in the data. The fluctuations in the price appear to be more practical as these fluctuations are stationary. In order to compute all parameters contained in fractional geometric Brownian motion and fractional Orenstein-Uhlenbeck, we obtained log return of adjust closed, daily volatility of log return and daily volatility of adjust closed. Figure 1 and Figure 2 show the price and return series.

The values of all parameters of the return series can be found in Table 1.

4.4. Estimation Based on Proposed Method

In this subsection we present the results of our study of modeling the data of KLCI, between the 3rd of January 2005 and 29th of December 2006 using GFBM by the assumption of stochastic volatility based on daily return series.

We used the parameters in Table 1 in order to compute the value of stochastic volatility. We depend on the equation to compute stochastic volatility for 100 times and then we compute

the average. We adopt this average value to be the volatility. With respect to long memory parameters are estimated by already command in |Mathematica 10 software. Finally, we obtained the following results and.

4.5. Calculating the Value of European Call Option

With the purpose of calculate the value of European call option, we use several maturity times (days) for a traded option. According to with the actual Malaysia conventional interest rate on 29th of December, 2006, the risk-free interest rate is fixed at 3.5% per annum. We consider MYR1096.24, following the price on 29 December, 2006 as the underlying price. The volatility and Hurst exponent are estimated based on our method for the historical daily return data of KLCI, with estimates listed subsection 4.3 to compare our work with others, we calculated the value of European call option using the estimates based on the methods of Masnita [1] , [2] and Kukush [3] , in addition to the traditional Black-Scholes European option price. The results are listed in Table 2.

From Table 2, it is clear that the longer time to expiry means the higher value of call price. The reader can observe that the call price of the proposed method of this work is closed to Masnita work and there is fairly different with Kukush et al. and traditional Black-Sholes. Call prices obtained by Kukush et al. with the R/S analysis, presents the lowest values. While the highest value calculated by traditional Black-Sholes model where the long memory is not taken into account. The prices which valued by proposed method and Masnita method are between those valued by the method of Kukush et al. and traditional Black-Scholes. However the method of Masnita is based on theoretical reasoning, but the volatility is assumed to be constant which was rejected by empirical studies as previously explained in chapter one [5] [6] [8] , whereas our model assumed that the volatility is stochastic and this is agree with empirical studies [9] - [14] [25] [26] .

5. Summary

We presented a new model which is a GFBM providing that the volatility is assumed stochastic that obeys fractional Orenstein-Uhlenbeck process. To estimate the parameters involved in this model, we have to maximize the likelihood function. Regrettably, the analytic solution of likelihood function is very hard, since the covariance function is very expensive. According to this we used innovation algorithm to simplify the problem. This leads to converting the likelihood function to constrained problem with some constrains. These constrains are appended to cost function using constraints transcription method which obtain unconstrained optimization problem. Finally, we solved the unconstrained optimization problem.

In order to know the performance of the proposed model with respect to other methods we calculated the value of European call option using the estimates based on the methods of Masnita [1] [2] , Kukush et al. [3] , traditional Black-Scholes European option price in addition to the proposed method. The results show that the call price of the proposed method of this work is closed to Masnita work and it is fairly different with Kukush et al. and traditional Black-Sholes.

Cite this paper

Mohammed Alhagyan,Masnita Misiran,Zurni Omar, (2016) Geometric Fractional Brownian Motion Perturbed by Fractional Ornstein-Uhlenbeck Process and Application on KLCI Option Pricing. Open Access Library Journal,03,1-12. doi: 10.4236/oalib.1102863

References

Appendix A: Simplification of the Model

Let represent the stock price process with the dynamic assumed by:

(A.1)

Let the dynamics of the volatility be described by fractional Ornstein-Uhlenbeck (FOU) process which is the solution of the following stochastic differential equation:

(A.2)

By using Euler’s discretization scheme for (A.2) we have:

(A.3)

Let then (A.3) covert to:

(A.4)

Assume and, then (A.4) can be written as:

(A.5)

Following the iteration process and Cauchy criterion (A.5) can be restated as:

(A.6)

Based on (A.6) the covariance of can be expressed as:

(A.7)

By sufficiently large L, (A.7) can be writing as:

(A.8)

where,

(A.9)

Now, return to equation (A.1), again by Euler’s discretization scheme, we get:

(A.10)

Let, then we get

(A.11)

Let , then we have

(A.12)

Assume that and then (A.12) become:

(A.13)

By (A.13) the covariance of can be expressed as:

(A.14)

Now we will compute every covariance function involved in (A.14)

(A.15)

where

(A.16)

(A.17)

But since and since and are independent. So (A.17) become

(A.18)

Similarly,

(A.19)

With respect of the last term

(A.20)

Finally,

(A.21)

For sufficiently large L (A.21) con be written as

(A.22)

NOTES

^*Corresponding author.