Materials Sciences and Applicatio n, 2011, 2, 1121-1126
doi:10.4236/msa.2011.28151 Published Online August 2011 (http://www.SciRP.org/journal/msa)
1121
Electronic States in Trans-CoCl2(H2O)4 Complex
Hajer Souissi1*, Souha Kammoun1
1Université de Sfax, Laboratoire de Physique Appliquée, Groupe de Physique Théorique, Département de Physique, Faculté des
Sciences de Sfax, Sfax, Tunisie.
Received March 7th, 2011; revised March 29th, 2011; accepted June 12th, 2011.
ABSTRACT
The polarized absorption spectra of cobalt(II) in trans-CoCl2(H2O)4.2H2O provides important information about the
electronic structure. Semi-empirical calculation of the crystal-field levels of the cobalt(II) with D4h point group symme-
try in CoCl2(H2O)4·2H2O are carried out, leading to a good agreement between the theoretical and experimental energy
levels.
Keywords: Crystal And Ligand Fields, Transition-Metal Compounds, Cocl2(H2O)4 Chromophore
1. Introduction
Several spectroscopic investigations of the transition
metal complexes with the trans-dichlorotetraaquo ligand
environment MCl2(H2O)4n+ (M: transition metal, M = V3+,
Ni2+, Co2+, Cr3+) are reported in literature [1-8]. For these
complexes, the bands of the absorption and luminescence
spectra are related to the transition metal ions M with 3dn
(n = 2, 3, 7, 8) configuration and originate from elec-
tronic transition in the unfilled 3d electronic shell. A de-
tailed crystal-field studies of the electronic energy levels
of trans-NiCl2(H2O)4, trans-VCl2(H2O)4+ and trans-
CrCl2(H2O)4+ complexes were presented in a recent work
[9-11]. These theoretical studies emphasized the impor-
tance of coupling between electronic states in the case of
the NiCl2(H2O)4 chromophore and of the Jahn-Teller
effect in the case of CrCl2(H2O)4+. Crystals of trans-CoCl2-
(H2O)4.2H 2O crystallize as regular monoclinic mauve
prisms [8,12]. Crystallographic studies confirm that
crystal of CoCl2(H2O)4.2H2O contain the trans-
CoCl2(H2O)4 chromophore where the Co2+(3d7) ions oc-
cupy a site with D4h symmetry [8]. A spectroscopic stud-
ies of the optical characteristics of trans-CoCl2(H2O)4
complex were presented by Bussière et al. [8]. In their
publications, the crystal field calculations based on the
angular overlap model (AOM) were performed for this
complex.
In this actual work, we present a detailed crystal-field
analysis of the electronic energy levels of trans-CoCl2
(H2O)4 complex. This analysis based on the Racah theory
was carried out for the Co2+ centre with a D4h site sym-
metry. The objective of this theoretical analysis is to de-
termine the Racah and the crystal-field parameters for the
CoCl2(H2O)4 chromophore, and, therefore, to deduce the
Stark levels which are not observed experimentally.
2. Experimental Support
The bases of our theoretical analysis will be the experi-
mental energy data obtained from the optical spectra of
trans-CoCl2(H2O)4 complex. For this reason, we present
briefly in this section the results of the spectroscopic
studies carried out by Bussière et al. at low temperature
[8,12]. The polarized absorption spectra of trans-
CoCl2(H2O)4 is measured at low temperature 5 K (Fig-
ure1) [8]. Three quartet bands are expected for Cobalt(II)
in octahedral symmetry : the first one is seen in the
near-infrared region of the spectrum around 8000 cm–1,
involving the 4T2g(4F) state. This band will be split into
4Eg and 4B2g in the D4h point group. The assignment of
the other two quartet bands is problematic and there are
substantial differences between the assignments given by
different authors [8]. For this reason Bussière et al. l de-
clare that this assignment is uncertain [8]. For a mixed
water and chloride ligand spheres, the 4A2g(4F) and 4T1g
(4P) states should be near a crossing point [8]. Bussière et
al.l have reported the 4A2g (4F) state to be at 16450 cm–1
(4B1g in D4h symmetry) and the 4T1g (4P) state, to be split
into 4Eg and 4A2g (in D4h symmetry) at 18600 and 22250
cm–1 corresponding to the strong bands in Figure 1. The
experimental energy levels are listed in Table 1. The
angular overlap model (AOM) [13] was used by Bussière
et al. in order to obtain the energetic order of quartet and
doublet excited states in this tetragonal chromophore.

Electronic States in Trans-CoCl(H O) Complex 1122 2 2 4
Table 1. Experimental and calculated energies (cm–1), and
AOM parameters (cm-1) of trans-CoCl2(H2O)4 [8].
Absorption 5 K
[{D4h} Oh (ion)] <polarization>
Calculated ligand-field
energies [D4h]
8060 [{4Eg} 4T2g(4F)]
8330 [{4B2g} 4T2g(4F)]
16450 [{4B1g} 4A2g(4F)]
18600 [{4Eg} 4T1g(4P)]
20268 [{2Eg} 2T1g(2P)]
22250 [{4A2g} 4T1g(4P)]
167 [ (Γ7) 4A2g]a
919 [4Eg]b
8054[4B2g]b
8297 [4Eg]b
16954 [4B1g]b
18805 [4Eg]b
20273 [Γ7]a
21167 [4A2g]b
aCalculated with

≠ 0; bCalculated with

= 0.
Figure 1. Polarized absorption spectra of trans-CoCl2(H2O)4
at 5 K [8].
The parameters eσ(H2O), eπS(H2O) and eπC(H2O) are set
to 4300, 1000 and 700 cm–1, respectively, while eσ(Cl)
and eπ(Cl) are set to 3300 and 1000 cm–1, respectively,
for the trans-CoCl2(H2O)4 complex. The Racah parameter
B was set to 824 cm–1 and the ratio C/B to 4.40. The cal-
culated energy levels by Bussière et al. of the
CoCl
2
(H
2
O)
4 chromophore are also listed in Table 1 [8].
3. Theoretical Background
3.1. Hamiltonian
The total Hamiltonian of 3dN ion in an arbitrary symme-
try site is written as [9-11]:
0CF SO
H
HH H (1)
H0 is the Coulomb interaction including elec-
tron-electron repulsions, this Hamiltonian gives the 2S+1L
terms: two quartet terms (4F ground state and 4P excited
state) and six doublet excited terms (2H, 2G, 2F, 2D, 2D’
and 2P). The eigenvalues of the Hamiltonian H0 are ex-
pressed as a function of the Racah parameters B and C
[14-15]. HSO is the spin-orbit coupling (
 is the SO pa-
rameter).
HCF is the crystal field Hamiltonian which can be rep-
resented quite simply as follows [14-15].
()
0
CF
kk
HB
kq q
kqk
C



(2)
where Bkq are the crystal-field parameters and are
the Racah tensor operators defined as follows :
()k
q
C
 
4
21
kq
C
q
l

Y
k
(3)
q
k
Y are the spherical harmonics.
For tetragonal symmetry site (D4h), the crystal-field
Hamiltonian HCF is invariant under this symmetry group.
The values of k and q permitted in the summations over k
and q in Equation (2), depend both on the D4h site sym-
metry and on the selection rules imposed to the matrix
elements of HCF [14-15]. So, the CF Hamiltonian HCF for
tetragonal symmetry D4h is given by:



(2)(4)(4) (4)
42004004444CF h
HDBCBC BCC

 (4)
For the CoCl2(H2O)4 complex a distorted octahedral
coordination geometry is observed leading to a lower
symmetry D4h [8]. Hence, the crystal field Hamiltonian
HCF(D4h) of Co2+(3d7) ions can be considered as the sum
of a dominant octahedral Hamiltonian HCF(Oh) and a
perturbation Hamiltonian
 HCF(D4h) translating the light
distortion. So in a D4h site symmetry, the Hamiltonian
HCF(D4h) takes the following form:
HCF(D4h) = HCF(Oh) +
 HCF(D4h) (5)
with:

(4)(4)( 4)
4044
5
() [14
cub
CF h
HO BCCC

 

(6-a)


(2)0(4)
42004CF h0
H
DBCBC (6-b)
with the z-axis taken along the C4 symmetry axis of
the octahedral and :
444
14
5
cub
BB , 0
4404
14
5
BB B 4 (7)
3.2. The Matrix Elements of the Crystal-Field
Hamiltonian
The effect of the CF Hamiltonian HCF on the energy lev-
els of the 3dN ion is studied by the degenerate perturba-
tion theory method. In first order perturbation theory, the
matrix associated to HCF can be diagonalized to find the
energy levels of the ion in the crystalline field. For this

Electronic States in Trans-CoCl(H O) Complex1123
2 2 4
reason, we give the method of calculation of the matrix
elements of the Hamiltonian HCF. Since for 3dN ions of
the first series in crystals the crystal-field is of the inter-
mediate strength [14-15], the basis functions


N
LS
dLSMM
in the LS-coupling scheme have been adopted in our
computer package. The CF Hamiltonian is developed as
a function of the Racah tensor . The matrix ele-
ments of operators are calculated numerically by
using the Racah tensor algebraic methods [14,15]:
()k
q
C
()k
q
C
() '
'
'
'
(1) '
L
k
LS qL S
LM k
LL
LSM MCLSMM
LL
kLSCL S
MM q






The 3j-symbols
'
'
LL
LL k
MM q




carry all the dependence on the labels ML, q and ML’
while the reduced matrix elements '
k
LSCLS is
independent of these labels, but depends on the normali-
zation of the tensor operators.
3.3. A Crystal-Field Analysis Computer Package
for 3dN (N = 2, 3, 7, 8) Ions
As a part of a larger project we have set to develop a
computer package based on Maple software to calculate
the energy levels and state vectors for any transition metal
ions with the 3dN configuration (N = 2, 3, 7, 8) located at
sites with symmetry given by any of the 32 crystallo-
graphic point groups. This computer package comprises
the following extensions: (1) the calculation of the matrix
elements of the crystal-field HCF by considering the
3j-symbols and the reduced matrix elements. (2) diago-
nalization of the full Hamiltonian matrices (taking into
account H0, HCF and HSO), this diagonalization yields the
energy levels as functions of the Racah parameters B and
C, crystal-field parameters Bkq and spin-orbit coupling
constant ξ. These parameters are regarded as empirical
parameters to be determined from the optical spectra. (3)
the determination of the Racah, crystal-field and spin-orbit
coupling parameters by minimising the gap between the
experimental and the theoretical energies. These parame-
ters allow us to deduce the calculated energy levels.
4. Results and Discussion
In this work, we are interested in the crystalline-field
splitting of the energy levels of Co2+(3d7) ions in
CoCl2(H2O)4 chromophore. The energetic contribution of
the Hamiltonian H0 + HCF(Oh) is dominant compared to
that of HCF(D4h) translating the light distortion. So, we
firstly determine the Racah parameter B and the octahe-
dral crystal-field parameter 4 from the mean values
of the observed spin-allowed bands in Oh symmetry
(<4T2g(4F)> = 8195 cm–1, <4A2g(4F) > = 18600 cm–1 and
<4T1g(4P) > = 22250 cm–1). These parameters are de-
duced from the eigenvalues obtained by diagonalising the
matrix 10 × 10 associated to the Hamiltonian H0 +
HCF(Oh) in the free-ion eigenstates
cub
B
,
L
LM within 4F
and 4P terms. According to Sugano et al. [16], the
(10-N)-electron system can be regarded as the N-hole sys-
tem. So, one can obtain the d7 matrix by changing the
signs of only the crystal-field matrix elements within the
complete energy matrix for the d3 configuration. The Ra-
cah parameter C is deduced from the observed
spin-forbidden bands in Oh symmetry and the eigenvalues
obtained by diagonalising the matrix 40 × 40 associated to
H0 + HCF(Oh) in the free-ion eigenstates ,
L
LM within
2H, 2G, 2F, 2D, 2D’ and 2P terms. The values of the Racah
and crystal-field parameters B, C and B4
cub
obtained are
listed in Table 2.
The calculated Oh energies for CoCl2(H2O)4 chromo-
phore are listed in Table 3. Then, the matrix elements of
the Hamiltonian perturbation HCF(D4h) are calculated
within the basis formed by the octahedral eigenstates.
The remaining crystal-field parameters B20 and were
calculated from the eigenvalues of the matrix associated
to HCF(D4h) and the observed bands at 8060 and 8330
cm–1 corresponding respectively to transitions from 4Eg
(4T1g(4F)) ground state to 4Eg(4T2g(4F)) and 4B2g(4T2g(4F))
excited states. The crystal-field parameters B20 and
obtained are respectively –540 cm–1 and –405 cm–1.
From equation 7, we deduce the values of the crys-
tal-field parameters B44 and B40. The spin-orbit coupling
constant λ (λ =  /3) considered in this work is similar to
that of reference [8]. The values of the crystal-field pa-
rameters B20, B40 and B44 and the spin-orbit coupling
constant λ are listed in Table 2. By using these parame-
ters, the diagonalization of the 120 × 120 matrix within
the quartet and doublet states associated to the Hamil-
tonien HCF(D4h) of equation 4 lead to the calculated en-
ergies for CoCl2(H2O)4 chromophore listed in Table 4.
0
4
B
0
4
B
Table 2. Racah and Crystal-field parameter values (cm–1)
for CoCl2(H2O)4 chromophore.
B
C
B4cub
B20
B40
B44
λ
948
3460
-19710
-540
-20115
-11778
-171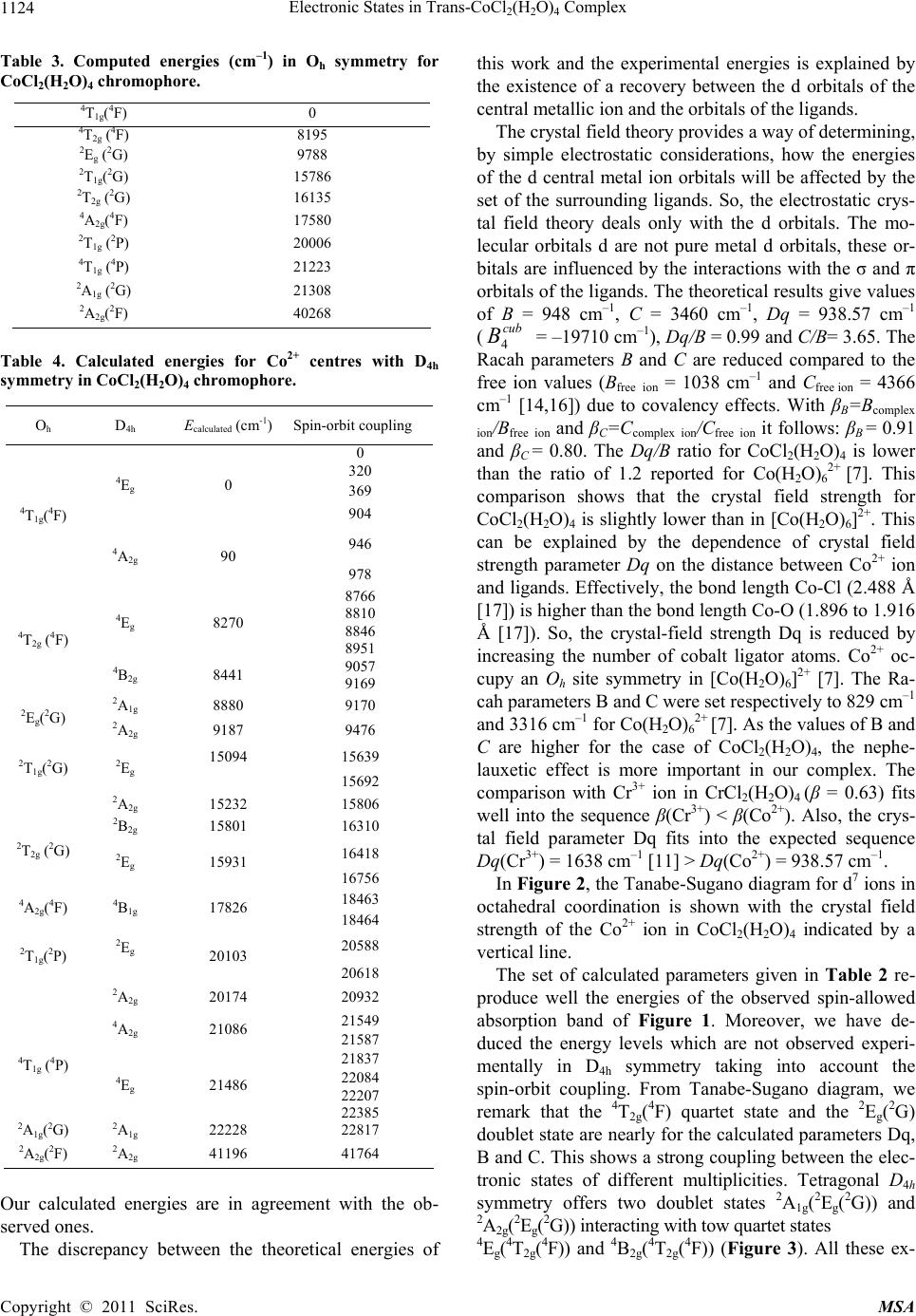

Electronic States in Trans-CoCl2(H2O)4 Complex 1124
Table 3. Computed energies (cm–1) in Oh symmetry for
CoCl2(H2O)4 chromophore.
4T1g(4F) 0
4T2g (4F)
2Eg (2G)
8195
9788
2T1g(2G) 15786
2T2g (2G) 16135
4A2g(4F) 17580
2T1g (2P) 20006
4T1g (4P) 21223
2A1g (2G) 21308
2A2g(2F) 40268
Table 4. Calculated energies for Co2+ centres with D4h
symmetry in CoCl2(H2O)4 chromophore.
Oh D
4h Ecalculated (cm-1) Spin-orbit coupling
0
320
369
4Eg 0
904
946
4T1g(4F)
4A2g 90
978
8766
8810
8846
4
Eg 8270
8951
9057
4T2g (4F)
4
B2g 8441 9169
2
A1g 8880 9170
2Eg(2G)
2
A2g 9187 9476
15094 15639
2T1g(2G) 2
Eg
15692
2
A2g 15232 15806
2B2g 15801 16310
16418
2T2g (2G)
2Eg 15931 16756
18463
4A2g(4F) 4
B1g 17826 18464
20588
2T1g(2P) 2Eg 20103
20618
2
A2g 20174 20932
21549
4
A2g 21086 21587
21837
22084
22207
4T1g (4P)
4
Eg 21486
22385
2A1g(2G) 2
A1g 22228 22817
2A2g(2F) 2
A2g 41196 41764
Our calculated energies are in agreement with the ob-
served ones.
The discrepancy between the theoretical energies of
this work and the experimental energies is explained by
the existence of a recovery between the d orbitals of the
central metallic ion and the orbitals of the ligands.
The crystal field theory provides a way of determining,
by simple electrostatic considerations, how the energies
of the d central metal ion orbitals will be affected by the
set of the surrounding ligands. So, the electrostatic crys-
tal field theory deals only with the d orbitals. The mo-
lecular orbitals d are not pure metal d orbitals, these or-
bitals are influenced by the interactions with the σ and π
orbitals of the ligands. The theoretical results give values
of B = 948 cm–1, C = 3460 cm–1, Dq = 938.57 cm–1
( = –19710 cm–1), Dq/B = 0.99 and C/B= 3.65. The
Racah parameters B and C are reduced compared to the
free ion values (Bfree ion = 1038 cm–1 and Cfree ion = 4366
cm–1 [14,16]) due to covalency effects. With βB=Bcomplex
ion/Bfree ion and βC=Ccomplex ion/Cfree ion it follows: βB = 0.91
and βC = 0.80. The Dq/B ratio for CoCl2(H2O)4 is lower
than the ratio of 1.2 reported for Co(H2O)62+ [7]. This
comparison shows that the crystal field strength for
CoCl2(H2O)4 is slightly lower than in [Co(H2O)6]2+. This
can be explained by the dependence of crystal field
strength parameter Dq on the distance between Co2+ ion
and ligands. Effectively, the bond length Co-Cl (2.488 Å
[17]) is higher than the bond length Co-O (1.896 to 1.916
Å [17]). So, the crystal-field strength Dq is reduced by
increasing the number of cobalt ligator atoms. Co2+ oc-
cupy an Oh site symmetry in [Co(H2O)6]2+ [7]. The Ra-
cah parameters B and C were set respectively to 829 cm–1
and 3316 cm–1 for Co(H2O)62+ [7]. As the values of B and
C are higher for the case of CoCl2(H2O)4, the nephe-
lauxetic effect is more important in our complex. The
comparison with Cr3+ ion in CrCl2(H2O)4 (β = 0.63) fits
well into the sequence β(Cr3+) < β(Co2+). Also, the crys-
tal field parameter Dq fits into the expected sequence
Dq(Cr3+) = 1638 cm–1 [11] > Dq(Co2+) = 938.57 cm–1.
cub
B4
In Figure 2, the Tanabe-Sugano diagram for d7 ions in
octahedral coordination is shown with the crystal field
strength of the Co2+ ion in CoCl2(H2O)4 indicated by a
vertical line.
The set of calculated parameters given in Table 2 re-
produce well the energies of the observed spin-allowed
absorption band of Figure 1. Moreover, we have de-
duced the energy levels which are not observed experi-
mentally in D4h symmetry taking into account the
spin-orbit coupling. From Tanabe-Sugano diagram, we
remark that the 4T2g(4F) quartet state and the 2Eg(2G)
doublet state are nearly for the calculated parameters Dq,
B and C. This shows a strong coupling between the elec-
tronic states of different multiplicities. Tetragonal D4h
symmetry offers two doublet states 2A1g(2Eg(2G)) and
2A2g(2Eg(2G)) interacting with tow quartet states
4Eg(4T2g(4F)) and 4B2g(4T2g(4F)) (Figure 3). All these ex-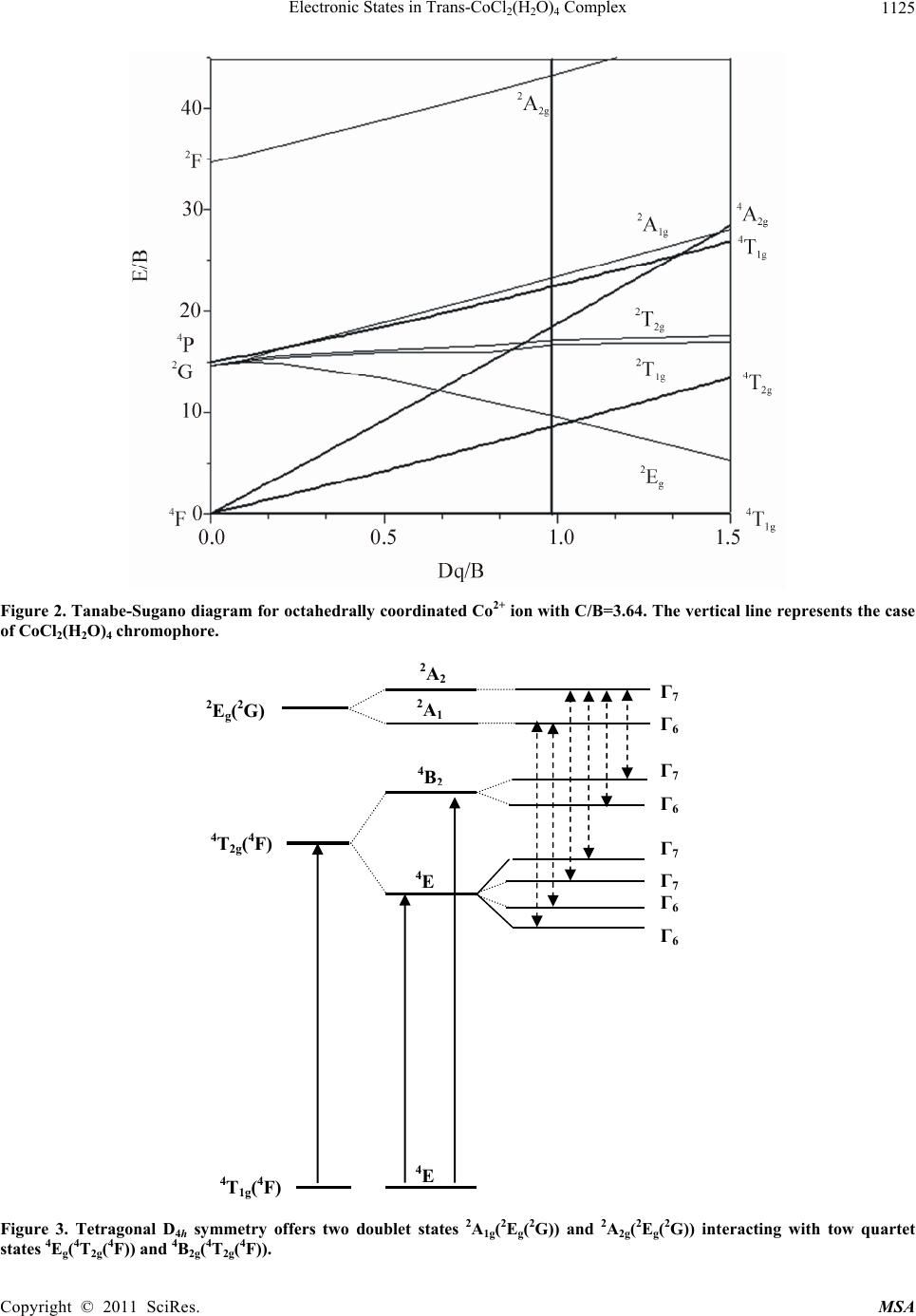

Electronic States in Trans-CoCl(H O) Complex 1125
2 2 4
Figure 2. Tanabe-Sugano diagram for octahedrally coordinated Co2+ ion with C/B=3.64. The vertical line represents the case
of CoCl2(H2O)4 chromophore.
Figure 3. Tetragonal D4h symmetry offers two doublet states 2A1g(2Eg(2G)) and 2A2g(2Eg(2G)) interacting with tow quartet
tates 4Eg(4T2g(4F)) and 4B2g(4T2g(4F)). s
4E
4T2g(4F)
4B
2
Γ7
Γ7
Γ6
Γ6
Γ7
Γ6
2A
2
Γ7
2Eg(2G) 2A
1
Γ6
4E
4T1g(4F)

Electronic States in Trans-CoCl(H O) Complex 1126 2 2 4
cited states are subdivided into doublet Kramer’s states Γ6
and Γ7 by spin-orbit coupling. The interaction between the
same symmetry levels Γ6 and Γ7 deriving from electronic
states of different multiplicities leads to the observed
spin-forbidden transition 4T1g(4F) → 2Eg(2G) (Oh symmetry)
with lower intensity compared to a spin-allowed transition
(Figure 3). The same explanation is also applied for the
4A2g(4F) quartet state and the 2T1g(2G) and 2T2g(2G) doublet
states.
5. Conclusions
A theoretical crystal-field analysis, based on the Racah
theory, was carried out for the electronic energy levels of
CoCl2(H2O)4. The observed crystalline-field splittings of
the Co2+ levels were accounted by using a D4h symmetric
Hamiltonian. As a result, Racah and crystal field parame-
ters have been reliably obtained. Calculated crystalline
field levels are in agreement with the observed ones. The
theoretical study confirms the charge state Co2+ of cobalt
and the site occupied D4h. The assignment of the first
quartet band 4T2g(4F) seen in the near-infrared region is in
agreement with the literature. Whereas, we find that the
assignment of the two other quartet bands are respectively
4A2g(4F) and 4T1g(4P). This assignment is uncertain in the
literature.
REFERENCES
[1] C. Reber, “Absorption and Luminescence Spectroscopy of
Transition Metal Compounds: from Coordination Geome-
tries to Exited-State Properties,” Canadian Journal of Ana-
lytical Sciences and Spectroscopy, Vol. 53, 2008, pp.
91-101.
[2] E. González, A. Rodrigue-Witchel and C. Reber, “Absorp-
tion Spectroscopy of Octahedral Nickel(II) Complexes: A
Case Study of Interactions between Multiple Electronic Ex-
cited States,” Coordination Chemistry Reviews, Vol. 251,
2007, p. 351.
doi:10.1016/j.ccr.2006.08.011
[3] R. Beaulac and C. Reber, “Spectroscopic Effects of Ex-
cited-State Coupling in a Tetragonal Chromonium (III)
Complex,” Inorganic Chemistry, Vol. 47, No. 12, 2008, pp.
5048-5054. doi:10.1021/ic702281k
[4] G. Bussière, C. Reber, D. Neuhauser, D. A. Walter and J. I.
Zink, “Molecular Properties Obtained by Analysis of Elec-
tronic Spectra Containing Interference Dips. Comparisons
of Analytical Equations and Exact Models Based on Cou-
pled Potential Energy Surfaces,” Journal of Physics Chem-
istry A, Vol. 107, 2003, pp. 1258-1265.
doi:10.1021/jp0218490
[5] P. L. W. Tregenna-Pigott, S. P. Best, H. U. Gudel, H.
Weihe and C. C. Wilson, “Influence of the Mode of Water
Coordination on the Electronic Structure of the [V(OH2)6]3+
Cation,” Journal of Solid State Chemistry, Vol. 145, 1999,
p. 460. doi:10.1006/jssc.1999.8154
[6] R. Meier, M. Boddin, S. Mitzenheim, V. Schmid and T.
Schonherr, “Elucidation of V(III) Complex Coordination
Numbers by Electronic Spectra,” Journal of Inorganic
Biochemistry, Vol. 69, No. 4, 1998, pp. 249-252.
doi:10.1016/S0162-0134(97)10031-9
[7] T. Schonherr, V. Schmid and R. Meier, “Study on Coordi-
nation Numbers Six and Seven in V(III) Complexes with
Aquo, Cyanide and Aminopolycarboxylic Ligands by
Means of the Angular Overlap Model,” Spectrochimica
Acta Part A, Vol. 54, No. 11, 1998, pp. 1659-1669.
doi:10.1016/S1386-1425(98)00094-8
[8] G. Bussière, R. Beaulac, B. Cardinal-David and C. Reber,
“Interacting Electronic States in Trans-MCl2(H2O)4n+ Com-
plexes (M: V3+, Cr3+, Ni2+, Co2+),” Coordination Chemistry
Reviews, Vol. 219-221, 2001, pp. 509-543.
[9] S. Kammoun, M. Dammak, R. Maalej and M. Kamoun,
“Crystal-Field Analysis for D8 ions at D4h Symmetry Sites:
Electronic States in Trans-NiCl2(H2O)4 Complex,”
Journal
of Luminescence, Vol. 124, No. 2, 2007, pp. 316-320.
doi:10.1016/j.jlumin.2006.04.006
[10] S. Kammoun, M. Dammak, R. Maalej, M. Kamoun. “Elec-
tronic States of Vanadium(III) in Trans-VCl2(H2O)4+ Chro-
mophore,” Journal of Alloys and Compounds, Vol. 453, No.
1-2, 2008, pp. 64-68.
doi:10.1016/j.jallcom.2006.11.180
[11] H. Souissi and S. Kammoun, “Theoretical Studyoftheelec-
Tronicstructureofa Tetragonal chromium(III)complex,” Jour-
nal of Luminescence, Vol. 131, No. 12, 2011, pp. 2515-
2520. doi:10.1016/j.jlumin.2011.05.044
[12] G. Bussière, C. Reber, “Coupled Excited States in Nickel(II)
Complexes Probed by Polarized Absorption Spectroscopy,”
Journal of American Chemistry Society, Vol, 120, No. 25,
1998, pp. 6306. doi:10.1021/ja9740733
[13] M. A. Hitchman, R. G. McDonald, P. W. Smith and R.
Stranger, “Electronic Spectrum and Metal-Ligand Bonding
Parameters of the V(H2O)63+ Ion,” Journal of Chemistry
Socience Dalton Transition, 1988, pp. 1393-1395.
doi:10.1039/dt9880001393
[14] R. C. Powell, “Physics of Solid-State Laser Materials,”
Springer-Verlag, New York, 1998.
[15] D. J. Newman and B. Ng, “Crystal Field Handbook,” Cam-
bridge University Press, Cambridge, 2000.
[16] S. Sugano, Y. Tanabe and H. Kamimura, “Multiplets of
Transition-Metal Ions in Crystals,” Academic Press, New
York, 1970.
[17] F. A. Cotton, C. A. Murillo and X. Wang, “Linear Tricobalt
Compounds with Di-(2-pyridyl)amide (dpa) Ligands: stud-
ies of the paramagnetic Compound Co3(dpa)4Cl2 in Solu-
tion,” Inorganic Chemistry, Vol. 38, 1999, pp. 6294-6297.
doi:10.1021/ic990944t