Journal of Power and Energy Engineering
Vol.04 No.07(2016), Article ID:69754,9 pages
10.4236/jpee.2016.47004
Hybrid and Reflective Insulation Assemblies for Buildings
David W. Yarbrough1, Khar San Teh2, Lim Chin Haw3, Elias Salleh3, Sohif Mat3, M. Yusof Sulaiman3
1R&D Services, Inc., Cookeville, TN, USA
2San Miguel Yamamura Woven Products, Air Keroh, Malaysia
3Solar Energy Research Institute (SERI), Universiti Kebangsaan, Bangi, Malaysia



Received 27 February 2016; accepted 25 July 2016; published 28 July 2016

ABSTRACT
Materials with a low thermal emittance surface have been used for many years to create reflective insulations that reduce the rate of heat flow across building envelopes. Reflective insulation technology is now being combined with other energy conserving technologies to optimize overall thermal performance. The basis for the performance of reflective insulations and radiant barriers will be discussed along with the combination of these materials with cellular plastic or mineral fiber insulations to form hybrid insulation assemblies. Calculations of thermal resistance for enclosed reflective air spaces and current field data from Southeast Asia will be presented. These data show that reductions in heat transfer across the building enclosure can be effectively reduced by the use of enclosed reflective air spaces and attic radiant barriers. Reflective technology increases the overall thermal resistance of the building enclosure when used to insulate poured concrete structures.
Keywords:
Reflective Insulation, Radiant Barrier, Hybrid Insulation, Emittance, Emissivity, Aluminum Foil, Metallic Films, Attic Insulation

1. Introduction
Enclosed reflective air spaces have significant thermal resistance making them useful as thermal insulation for a building enclosure. The term reflective air space means that there is at least one surface with low emittance (emissivity), ε, perpendicular to the direction of heat flow. The statement “enclosed space” means that air is not moving in or out of the space. The low-emittance surface is commonly provided by polished aluminum foil with total hemispherical emittance in the range 0.03 to 0.05 or metallized polymer film with a coating for protection against oxidation with emittance in the range 0.04 to 0.06. The radiative heat flux, qrad, across an air space (net heat transfer by radiation from a warm surface at absolute temperature T1 to a cool surface at absolute temperature T2) can be calculated for large parallel surface using Equation (1), the Stefan-Boltzmann Law [1], with an effective emittance, E, shown as Equation (2) [2] [3].
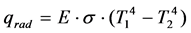 (1)
(1)
 (2)
(2)

The radiative heat flux, qrad, is readily calculated from the above equations for large parallel surfaces and used to estimate the radiative flux for enclosed regions in the building enclosure. Table 1 contains E values for three commonly encountered building configurations. An emittance of 0.9 is commonly used for non-metallic building materials such as concrete, masonry composites, or wood. The reduction in Qrad is directly proportional to the reduction in E.
The total heat flow across an air space includes conduction and convection in addition to radiation. For small air spaces, convective transport is often negligible and the sum of radiative and conductive heat transport can be readily calculated [4]. Figure 1 shows % reduction relative to E = 0.818 as a function of E for heat flow by radiation and conduction across a 15-mm airspace with an average temperature 30˚C and a temperature difference 10˚C.
2. Total Heat Flow across a Reflective Insulation Assemble
The RSI (m2∙K/W) for a large planar enclosed air space depends on several variables. Table 2 lists these variables along with their relative importance.
The total steady-state heat flux, qtotal for an enclosed region can be obtained from Equation (3) where the dimensionless Nusselt Number, Nu (=h∙L/λ), is the ratio of the heat flux for conduction plus convection to the heat flux for conduction where the characteristic length, L, is the distance across the enclosed region in the direction of heat flow. Equation (4) is of practical important since it shows how Nu can be obtained from measurements of qtotal. The total heat flux across a building element can be determined from a hot-box measurement [5] [6] using well-established procedures for correcting for support materials [7] [8].
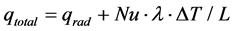 (3)
(3)
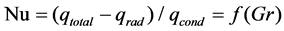 (4)
(4)
Correlations for Nu in terms of the dimensionless Grashoff Number, Gr, which is ΔT∙L3∙gc/T∙γ2 where T is the
Table 1. E for three material combinations.
Table 2. Factors that affect RSI for a reflective insulation assemble.
Figure 1. Heat flow by radiation and conduction is reduced as effective emittance is reduced.
absolute temperature and γ is the kinematic viscosity of air at the average temperature of the space. The function f in Equation (4) which depends on the heat flow direction has been determined from a large number of hot box tests for heat flow: up, 45˚ up, horizontal, 45˚ down, and down [9] [10]. Correlations for Nu make it possible to calculate the total heat flux across a single air space and RSI for the space since RSI is the ratio of ΔT to qtotal. Enclosed reflective air spaces in series can also be calculated be an iterative procedure in which the total temperature difference is partitioned into {ΔTi} where the subscript indicates the ith air space.
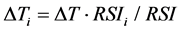 (5)
(5)

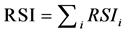
The calculation of the set {RSIi} can be accomplished using the Method of Successive Approximations with a starting set {ΔTi} taken to be equal to fi∙ΔT where fi is the fraction of the total space occupied by region i. A correction based on radiation intersecting supporting materials between the warm and cool surfaces can be made using an analysis from Glicksman [11]. Table 3 contains results for a 25 mm enclosed air space at average temperature 30˚C, a temperature difference of 10˚C, and E = 0.03 for each enclosed air space. The results in Table 3 show the advantage of multilayer reflective systems and an example of the impact of the radiation correction in the case of horizontal heat flow. The RSI for the reflective insulation material was taken to be zero. The calculation can be easily modified to account for the thermal resistance contributed by the reflective insulation material when the thermal resistance of the material is not negligible.
3. Radiant Barriers and Ceiling Heat Flux
A ventilated space in a building with a low-emittance surface facing the space is called a radiant barrier system (RBS) [12]. This type of application reduces the radiative heat transfer across the space with the greatest impact being reduction in the heat flow across the space during hot weather. Figure 2 contains diagrams showing two RBS applications. The ceiling below the attic space has been removed for these photographs.
The thermal performance of RBS is generally determined from computer simulations of the heat flow and air movement in the ventilated space [13]-[15]. There have been a large number of field tests completed in recent years to determine the benefits of RBS [16]. Table 4 contains some examples of the results that have been obtained. Table 4 also contains steady-state heat flux reductions for RBS determined using a hot-box facility operated in both summer and winter conditions [17]. The field-tests provide results that depend on the climate while the hot-box measurement is a steady-state test.
Table 3. RSI for a 25 mm vertical enclosed air space.
Table 4. Ceiling heat flux reductions due to presence of a radiant barrier.
Figure 2. Radiant barrier systems between the ceiling and roof of a building enclosure.
4. Field Testing of Radiant Barrier Systems in Malaysia
Figure 3 contains a photograph of three identical test huts that are being used to study the performance of radiant barriers in the space between the roof and the ceiling. A radiant barrier is a material with a low thermal emittance surface that is located next to a large air space. The low emittance (high reflectance) material significantly reduces heat transfer across the air space next to the surface. The reduction in radiative heat flow occurs in all seasons as suggested by Equation (1).
Figure 4 contains a photograph of the heat flux transducer employed and a diagram of showing the location of the transducer. Figure 5 shows the location of the Type K thermocouples used for temperature measurements.
The instrumentation in the test huts allows a record of temperatures and heat flux, q, across the ceiling in each unit. These data are used in Equation (6) to calculated U-value based on the area of the ceiling C. The corresponding overall thermal resistant can be obtained from the reciprocal of U.
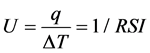 (6)
(6)
If the average ΔT is calculated for the region between the ceiling and the radiant barrier material (the attic space), then the result is the U and RSI for the attic space.
An attic radiant barrier reduces the temperature on the inside of the unconditioned test huts. As an example, when the outside air temperature was 37.1˚C, the maximum interior temperature without a radiant barrier was observed to be 38.8˚C. The interior hut temperatures were reduced to 33.9˚C or 35.7˚C depending on the type of radiant barrier that was installed. The lower interior temperature was observed with a radiant barrier that has a small intrinsic (material) RSI-value. Figure 6 shows transient R-values used to calculate RSIave. These data show the increase in RSI that result in the reduction in air conditioning that would be needed to maintain a constant temperature space below the ceiling; an energy conserving feature. The vertical axis is the measured
Figure 3. Three identical test huts for comparative studies of heat flow with radiant barriers.
Figure 4. Photograph of HFT and a diagram showing location of heat flux transducer.
R-value at the time indicated by the horizontal axis. The blue data are for a test hut with no radiant barrier. The red and green data are for huts with a radiant barrier installed between the roof deck and the ceiling. The negative heat flux data occurs at night when the hut is cooling and heat is being transferred to the outside. These data
Figure 5. Diagram of test hut showing thermocouple locations.
Figure 6. RSI for a test hut without radiant barrier (blue) and two test huts with radiant barrier material (red and green).
are used in Equation (6) along with the temperature difference to calculated RSI at a specific time.
The average RSI, RSIave, is obtained over a time period (t1, t2) using Equation (7) for n data points taken at even time steps, Δt.

5. Hybrid Assemblies that Include an Enclosed Reflective Air Space
Enclosed reflective air spaces (Reflective Insulation Systems) ae commonly used to add thermal resistance to the low thermal resistance of masonry walls (blocks or poured concrete). This is accomplished by attaching spacers
to the interior surface of the wall to provide space for the reflective insulation. The reflective insulation is installed between the spacers. Figure 7 shows reflective insulation on the interior side of a concrete wall. Figure 8 is a photograph of a building that uses this type of insulation. The diagram in Figure 7 shows the location of a reflective insulation that has two reflective air spaces when the thickness is 19 mm and three reflective air spaces when the thickness is 38 mm. The 19 mm space has RSI 0.88 while the 38 mm space has RSI = 1.23.
Figure 9 contains a diagram of a “hybrid Assembly” that combines a conventional insulation (fibrous insulation or cellular plastic insulation) with a reflective insulation that creates three enclosed reflective air spaces. The thermal resistances which are additive are shown in Figure 10 for a range of insulating foam thicknesses and thermal resistivities, RSI* (RSI for 25.4 mm of foam thickness). The foam insulation contribution to the total RSI is readily calculated from the given data and the contribution of the reflective component can be obtained by difference.
Figure 7. Diagram showing reflective insulation on concrete wall.
Figure 8. Photograph of building with reflective masonry insulation.
Figure 9. Diagram of an advanced hybrid insulation assembly. Top arrow identifies fiberglass insulation. The bottom arrows show three enclosed reflective air spaces (diagramcourtesy of Fi-Foil Company, Auburndale, FL, USA).
Figure 10. Total thermal resistance (RSI) for hybrid assembly combining foam and a three-layer reflective insulation like that in a wall application.
6. Conclusion
The thermal resistance attributed to enclosed reflective air spaces is readily calculated from published correlations representing a large number of hot-box tests. Multiple enclosed reflective air spaces significantly increase the thermal resistance that can be created in a given region in the building envelope. Low-emittance material (radiant barriers) installed between the roof and ceiling in a structure with a low emittance surface facing the attic space significantly reduces the transport of heat across the air space and the ceiling. Insulations can be combined to create hybrid insulation systems with high thermal resistance and demonstrated energy conservation potential.
Acknowledgements
The authors extend thanks to William A. Lippy, President, Fi-Foil Company USA and San Miguel Yamamura Woven Products Malaysia and the Universiti Kebangsaan Malaysia for use of graphics and test data.
Cite this paper
David W. Yarbrough,Khar San Teh,Lim Chin Haw,Elias Salleh,Sohif Mat,M. Yusof Sulaiman, (2016) Hybrid and Reflective Insulation Assemblies for Buildings. Journal of Power and Energy Engineering,04,23-31. doi: 10.4236/jpee.2016.47004
References
- 1. Siegal, R. and Howell, J.R. (1972) Thermal Radiation Heat Transfer. McGraw-Hill Book Company, Inc. New York, 188-190.
- 2. 2013 ASHRAE Handbook-Fundamentals, ASHRAE 1721 Tullie Circle, NE, Atlanta, Note e, 26.14.
- 3. Bird, R.B., Stewart, W.F. and Lightfoot, E.N. (1965) Transport Phenomena. John Wiley &Sons, Inc., New York, 446- 447.
- 4. Yarbrough, D.W. (20100 Reflective Materials and Radiant Barriers for Insulation in Buildings, Chapter 12 in Materials for Energy Efficiency and Thermal Comfort In Buildings Edited by Matthew R. Hall, CRC Press, New York, 305-318.
- 5. ASTM C1363 (2015) Standard Test Method for Thermal Performance of Building Materials and Envelope Assemblies by Means of a Hot Box Apparatus. Annual Book of ASTM Standards 04.06, American Society for Testing and Materials, West Conshohocken, 775-818.
- 6. ISO 8990:1994E (1994) Thermal insulation-Determination of steady thermal transmission properties-Calibrated and Guarded Hot Box. The International Organization for Standardization, Geneva.
- 7. ASTM C1224 (2015) Standard Specification for Reflective Insulation for Building Applications. Annual Book of ASTM Standards 04.06, American Society for Testing and Materials, West Conshohocken, 687-691.
- 8. 2013 ASHRAE Handbook-Fundamentals, ASHRAE 1721 Tullie Circle, NE, Atlanta, 25.7.
- 9. Robinson, H.E. and Powell, F.J. (1956) The Thermal Insulating Value of Airspaces. Housing Research Paper 32, United States National Bureau of Standards Project ME-12, US Government Printing Office, Washington DC.
- 10. Desjarlais, A.O. and Yarbrough, D.W. (1991) Prediction of the Thermal Performance of Single and Multi-Airspace Reflective Insulation Materials. ASTM STP 1116, Graves, R.S. and Wysocki, D.C., Eds., American Society for Testing and Materials, West Conshohocken, 24-42.
- 11. Glicksman, L.R. (1991) Two-Dimensional Heat Transfer Effects on Vacuum and Reflective Insulation. Journal of Thermal Insulation, 14, 281-294. http://dx.doi.org/10.1177/109719639101400404
- 12. ASTM C168 (2015) Standard Terminology Relating to Thermal Insulation. Annual Book of ASTM Standards 04.06, American Society for Testing and Materials, West Conshohocken, 16-22.
- 13. ASTM C1340 (2015) Standard Practice for Estimation of Heat Gain or Loss Through Ceilings Under Attics Containing Radiant Barriers by Use of a Computer Program. Annual Book of ASTM Standards 04.06, American Society for Testing and Materials, West Conshohocken, 776-797.
- 14. Saber, H.H. (2013) Thermal Performance of Wall Assemblies with Low Emissivity. Journal of Building Physics, 36, 308-329. http://dx.doi.org/10.1177/1744259112450419
- 15. Han, B.J., Yarbrough, D.W. and Han, S.M. (1985) Thermal Resistance of Wall Cavities Containing Reflective Insulation, HTD-Vol. 41. The American Society of Mechanical Engineers, 39-44.
- 16. Medina, M. (2012) A Comprehensive Review of Radiant Barrier Research Including Laboratory and Field Experiments. ASHRAE Transactions, 118 Part 1.
- 17. Shrestra, S., William Miller, W. and Desjarlais, A. (2013) Thermal Performance Evaluation of Attic Radiant Barrier Systems Using the Large Scale Climate Simulator (LSCS). Proceedings of the International Conference on Thermal Performance of the Exterior Envelopes of Whole Buildings XII.












