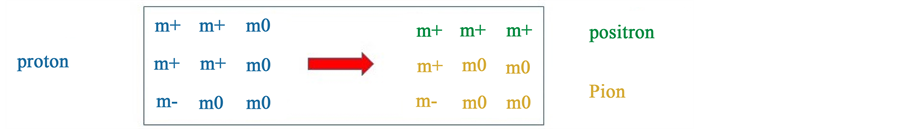Open Access Library Journal
Vol.03 No.07(2016), Article ID:69568,5 pages
10.4236/oalib.1102788
Standard Model Matter Emerging from Spacetime Preons
Risto Raitio
Espoo, Finland

Copyright © 2016 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 1 June 2016; accepted 26 July 2016; published 29 July 2016

ABSTRACT
I consider a statistical mechanical model for black holes as atoms of spacetime with the partition function sum taken over area eigenvalues as given by loop quantum gravity. I propose a unified structure for matter and spacetime by applying the area eigenvalues to a black hole composite model for quarks and leptons. Gravitational baryon number’s non-conservation mechanism is predicted. Argument is given for unified field theory based on gravitational and electromagnetic interactions only. The standard model of non-Abelian gauge interactions is briefly discussed.
Keywords:
Quantum Black Hole, Statistical Mechanics, General Relativity, Loop Quantum Gravity, Hawking Radiation, Davies-Unruh Effect, Standard Model
Subject Areas: Particle Physics

1. Introduction
In this note I continue elaborating the statistical mechanical model for black holes discussed in [1] . The partition function is redefined as a sum over black hole stretched horizon area eigenvalues as given by Loop Quantum Gravity (LQG) [2] [3] . I propose a unified picture for matter based on the preon model for quarks and leptons [4] and the horizon model for atoms of spacetime [5] . Originally there were no phenomenological reasons to introduce the preon model. The reason was to find a common concept of origin for particles and spacetime, as described below. The history of quantum gravity indicates the need for some new ideas.
This note is organized as follows. In section 2 I present briefly the horizon model of black holes. In section 3 the main point of this schematic model, consistent quantum structure of matter and spacetime, is discussed. I apply a previous model for composite quarks and leptons, the constituents of which are defined by mass, spin and charge. The mass scale of preons is found to start from zero using the area eigenvalues of LQG. A reason for point-like particles is indicated. The model predicts a mechanism of the gravitational decay of the proton. This decay is due to an explicit preon rearrangement interaction instead of a general black hole quantum number erasure process. The preon model includes the electromagnetic U(1) gauge interaction and provides the fermion quantum number basis for the non-Abelian color and weak interactions. Finally in section 4 I give a brief discussion of results and conclusions. Being a scheme proposal the presentation is very concise throughout.
2. LQG Spacetime Area Eigenvalues
I consider a micro black hole dressed by a stretched horizon, which is a membrane hovering about a Planck length outside the event horizon and which is both physical and hot.
The energy of a black hole from the point of view of an observer on its stretched horizon is called Brown- York energy [6]
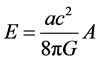 (2.1)
(2.1)
where a is the constant proper acceleration of an observer on the stretched horizon and A is the area of the horizon. In LQG the area eigenvalues are
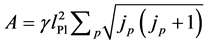 (2.2)
(2.2)
where the sum is over punctures p of the spin network, 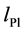 is the Planck length,
is the Planck length, 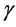 is the Barbero-Immirzi
is the Barbero-Immirzi
parameter and the values of 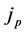 are
are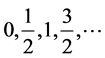 . For canonical treatments of quantum geometry and black
. For canonical treatments of quantum geometry and black
holes, see [7] [8] .
For the BH spacetime phenomenological model the partition function for a spin network with N punctures is, for details, see [5] .
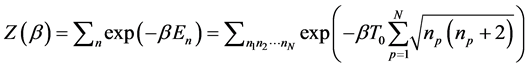 (2.3)
(2.3)
where 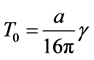 and
and , with
, with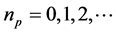 . The resulting
. The resulting 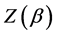 is [5]
is [5]
 (2.4)
(2.4)
where
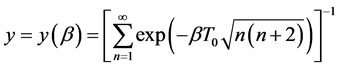 (2.5)
(2.5)
When 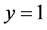 one has simply
one has simply .
.
The average energy at temperature 
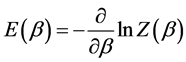
of the black hole which yields
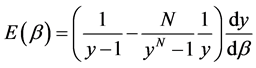
In LQG it is assumed that the number of punctures on the stretched horizon is very large, say about 10122. Therefore for 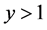
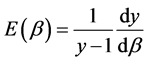
For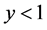
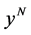
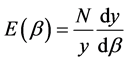
There is a jump in energy of the hole when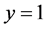

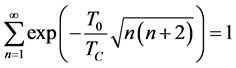
Below the critical temperature 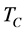
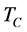
From 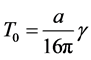

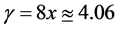
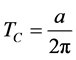
which is the Davies-Unruh temperature felt by an observer on the stretched horizon with constant acceleration a.
In Schwarzschild spacetime the line element includes the function 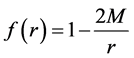
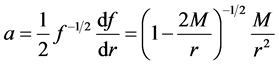
Right outside the horizon 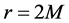
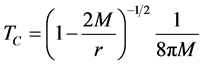
This temperature corresponds according to the Tolman relation a far away observer temperature
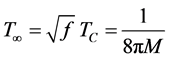
which is the Hawking temperature.
3. Model of Matter and the Unified Picture
The statistical model of Section 2 for spacetime offers a possibility to study the matter sector from a novel point of view to build a consistent, unified picture of matter and spacetime based on black holes. This goal would imply some internal structure at scale of the order of 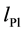
The basic idea of [4] is that the quarks and lepton are made of black holes, called maxons, with characterized by three quantum numbers: mass, spin and charge. Their values are: mass is the Planck mass, spin 1/2 and charge 0 or 1/3. In addition there is “color” (i, j, k) as a permutation index. The first generation quarks and leptons are the following bound states
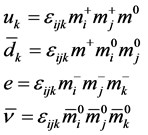
Charge quantization {0, 1/3, 2/3, 1} and particle permutation symmetry pull out of vacuum these standard model particles. States in (3.1) with only two identical maxons provide an index for quark three-valued color. I assume that these states are bound by gravitational (or other Planck scale) force between preons. Properties of this interaction need to be modeled as a future project. The question of existence of free single maxons depends on the details of the model.
The construction (3.1) is matter-antimatter symmetric on maxon level, which is desirable for early cosmology. The model makes it possible to create from vacuum a universe with only matter: combine e.g. six m+, six m0 and their antiparticles to make the basic β-decay particles, see Figure 1. Corresponding antiparticles occur equally well.
The maxon mass scale is the Planck scale and (3.1) would be superheavy particles. To get the standard model particles the large mass difference has to be explained. It is accomplished from (2.2) by setting jp = 0, which leads by (2.1) to zero mass “cold” black hole. This jp = 0 maxon may interact with the Higgs field and gain a light mass. Above the critical temperature, defined by (2.10), maxons should have a phase transition into Hawking radiating black holes.
The mass scale change is significant. It may be understood, using non-relativistic quantum mechanics as a guide, by assuming that when a maxon gets zero mass the spacetime geometry changes so that the maxon is trapped inside a rigid wall potential well of depth 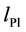
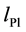
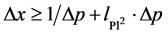
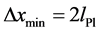
Spin 3/2 quarks and leptons are implied by this model.
The baryon number (B) is not conserved [10] - [12] in this model: a proton may decay at Planck scale temperature by a preon rearrangement process into a positron and a pion, see Figure 2. This is expected to be independent of the details of the preon interactions. Baryon number minus lepton number is conserved. One may speculate now that the ultimate grand unified theory is a preon theory with gravitational and electromagnetic interactions only. Basically, I have followed the guide of [10] that “black holes should be subject to the same rules of quantum mechanics as ordinary elementary particles or composite systems”.
The large mass reduction from Planck scale to zero would also imply shrinkage of the BH from three spatial dimensions to a point. Thus point-like particles would be dynamical consequence of quantum gravity.
Figure 1. Maxons, antimaxons and four particles.
Figure 2. Proton decay by maxon rearrangement.
The standard model gauge bosons and the Higgs would be elementary (but their composite nature is not ruled out). The three generations would be due to a gravitational mechanism or a new symmetry. Note that I have assumed the standard model on top of the present preon model. On the other hand, starting from the preon model, one can “derive” the SM from (3.1) and Figure 1: one gets color and the weak isodoublet quantum numbers, for fermions and therefore the correct N in SU(N) for strong and weak interaction gauge groups.
In the early universe at high temperature the standard model quarks and leptons would not be formed immediately. Instead all matter would be in black holes interacting gravitationally and electromagnetically. Quarks and leptons would appear later when the temperature decreases substantially. Electroweak and QCD interaction come to play rather late.
Some fraction of primordial black holes should remain black making dark matter. Their masses are expected to be around 30 solar masses. In [13] the authors discuss the possibility that LIGO has detected dark matter in black hole mergers..
4. Conclusion
There are at present a number of competing candidate theories for quantum gravity like string theory, loop quantum gravity, causal dynamical triangulation, and others. The model of Sections 2 and 3 goes deep into the structure of the physical universe and can be considered as a promising candidate for a unified scheme of “everything”, in the sense discussed here. In the scenario briefly outlined above, LQG area eigenvalues and the composite quark and lepton model look promising ingredients on the road towards the origin of spacetime, gravity and matter.
Cite this paper
Risto Raitio, (2016) Standard Model Matter Emerging from Spacetime Preons. Open Access Library Journal,03,1-5. doi: 10.4236/oalib.1102788
References
- 1. Raitio, R. (2016) A Statistical Model of Spacetime, Black Holes and Matter. Open Access Library Journal, 3, e2487.
http://dx.doi.org/10.4236/oalib.1102487 - 2. Chiou, D.-W. (2015) Loop Quantum Gravity. International Journal of Modern Physics D, 24, 1530005.
http://dx.doi.org/10.1142/S0218271815300050 - 3. Rovelli, C. (2011) Zakopane Lectures on Loop Gravity.
https://arxiv.org/abs/1102.3660 - 4. Raitio, R. (1980) A Model of Lepton and Quark Structure. Physica Scripta, 22, 197.
http://dx.doi.org/10.1088/0031-8949/22/3/002 - 5. Mäkelä, J. (2016) Phase Transition in Loop Quantum Gravity.
https://arxiv.org/abs/1604.01393
http://dx.doi.org/10.1103/physrevd.93.084002 - 6. Brown, J. and York Jr., J. (1993) Quasilocal Energy and Conserved Charges Derived from the Gravitational Action. Physical Review D, 47, 1407.
http://dx.doi.org/10.1103/PhysRevD.47.1407 - 7. Ashtekar, A., Baez, J., Corichi, A. and Krasnov, K. (1998) Quantum Geometry and Black Hole Entropy. Physical Review Letters, 80, 904-907.
https://arxiv.org/abs/gr-qc/9710007
http://dx.doi.org/10.1103/PhysRevLett.80.904 - 8. Barbero G., J.F. and Perez, A. (2015) Quantum Geometry and Black Holes.
http://arxiv.org/abs/1501.02963 - 9. Tawfik, A. and Diab, A. (2015) A Review of the Generalized Uncertainty Principle. Reports on Progress in Physics, 78, 126001.
http://dx.doi.org/10.1088/0034-4885/78/12/126001 - 10. ‘t Hooft, G. (1985) On the Quantum Structure of a Black Hole. Nuclear Physics B, 256, 727-745.
http://dx.doi.org/10.1016/0550-3213(85)90418-3 - 11. Bekenstein, J. (1972) Non Existence of Baryon Number for Static Black Holes I and II. Physical Review D, 5, 1239-1246.
- 12. Wheeler, J. (1971) Cortona Symposium on Weak Interactions. Academia Nazionale dei Lincei, Rome.
- 13. Bird, S., Cholis, I., Muñoz, J., Ali-Haïmoud, Y., Kamionkowski, M., Kovetz, E., Raccanelli, A. and Riess, A (2016) Did LIGO Detect Dark Matter?
http://arxiv.org/abs/1603.00464