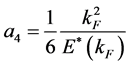Open Access Library Journal
Vol.03 No.07(2016), Article ID:69558,18 pages
10.4236/oalib.1102757
Landau Theory of Fermi Liquid in a Relativistic Nonlinear (σ, ω) Model at Finite Temperature
Schun T. Uechi1, Hiroshi Uechi2
1Department of Physics & Astronomy, The University of Georgia, Athens, GA, USA
2Osaka Gakuin University, Osaka, Japan

Copyright © 2016 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 21 May 2016; accepted 25 July 2016; published 28 July 2016

ABSTRACT
Fermi liquid properties of nuclear matter at finite temperature are studied by employing a relativistic nonlinear (σ, ω) model of quantum hadrodynamics (QHD). The relativistic nonlinear (σ, ω) model is one of the thermodynamically consistent QHD approximations. The QHD approximations maintain the fundamental requirement of density functional theory (DFT). Hence, the finite temperature nonlinear (σ, ω) mean-field approximation can be self-consistently constructed as a conserving approximation. Fermi liquid properties of nuclear matter, such as incompressibility, symmetry energy, first sound velocity and Landau parameters, are calculated with the nonlinear (σ, ω) mean-field approximation, and contributions of nonlinear interactions and finite temperature effects are discussed. Self-consistent structure to an employed approximation as conserving approximation is essential to examine physical quantities at finite temperature. Finite-tempera- ture effects are not large at high density, however, the Fermi ground state, density of states and Fermi-liquid properties may be varied noticeably with a finite temperature (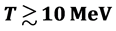 ) at low densities. Low-density finite-temperature and high-density finite-temperature experiments might exhibit physically different results, which should be investigated to understand nuclear many- body phenomena.
) at low densities. Low-density finite-temperature and high-density finite-temperature experiments might exhibit physically different results, which should be investigated to understand nuclear many- body phenomena.
Keywords:
Quantum Hadrodynamics (QHD), DFT in Nuclear Matter, Nonlinear Mean-Field Theory, Landau Parameters at Finite Temperature
Subject Areas: Nuclear Physics, Theoretical Physics

1. Introduction
Quantum hadronic theories of hot and dense nuclear matter have been applied to nuclear-structure properties such as proton-nucleus scattering and nuclear matter [1] - [5] , and problems of nuclear-astrophysics: neutron stars, baryon-hyperon phase transition, hadron-quark phase transition and quark-gluon plasma. Equations of state of nuclear and hyperonic matter are fundamental to examine properties of neutron star masses, radii, moments of inertia [6] - [8] . It is expected that the phase-transition temperature from hadronic phase to quark-gluon plasma should be of the order of T = 200 MeV, and it is hoped that head-on heavy-ion collision experiments may achieve physical values of defining hadron-quark phase transition [9] - [11] . In order to examine wide variety of hypothetical nuclear and astrophysical phenomena, one will need consistent microscopic many-body calculations based on a relativistic quantum field theory at finite temperature [12] [13] .
The dynamics of infinite hadronic matter can be checked against conditions of macroscopic conservation laws, such as, the virial theorem [14] , the first law of thermodynamics, Gibbs’ relation and the corresponding differential laws which are written covariantly [15] [16] . Macroscopic properties are expressed with particle density, energy density, pressure and entropy constructed from basic interactions of particles. Covariant formulations of thermodynamics and thermodynamic consistency in microscopic calculations are explicitly shown in a relativistic formalism. The consistency of microscopic calculations and validity of approximations can be examined through macroscopic conservation laws [17] - [23] .
Nuclear many-body theory states that even in the strong interaction region, the effect of the nuclear medium on a specific nucleon about the Fermi energy range can be described by a single particle energy that will be determined by microscopic interactions of particles. For all processes with energy near the Fermi energy, the nucleus may be considered as a gas of (quasi-) particles [4] [24] [25] , which satisfies macroscopic conservation laws, and we have a picture that self-consistently determined or dressed single particles move within the mean-field potential of nucleons. The dynamically determined single particle energy constructed from a basic Hamiltonian or a Lagrangean and the self-consistent single quasiparticle energy of nuclear matter must be equivalent at the Fermi surface, which is known as Landau’s requirement of quasiparticles [26] - [28] or the requirement of density functional theory (DFT) [29] [30] .
We employ a relativistic nonlinear (σ, ω) effective model of hadrons [8] [31] , extended from a relativistic quantum field theory, Quantum Hadrodynamics (QHD) [32] [33] , and the nonlinear mean-field approximation is applied to nuclear matter in order to investigate Fermi liquid properties of nuclear matter at finite temperature.
The mean-field approximation (Walecka model) to the theory of QHD produces a thermodynamically consistent field theoretical approximation. One can directly show that dynamical single particle energy defined in Green’s function and quasiparticle energy defined by Landau’s fundamental requirement are equal, and consequently, Fermi liquid properties of nuclear matter are discussed consistently at zero temperature [34] - [36] . The self-consistency, equality of dynamical and quasiparticle single particle energies, can be proved only if nonlinear interactions are properly renormalized. The fundamental requirement of conserving approximation or DFT is satisfied. The nonlinear (σ, ω) effective model is a conserving approximation [37] [38] , which is also essential for self-consistent finite temperature approximations. Nonlinear interactions should be properly renormalized as effective masses and effective coupling constants to be a conserving approximation.
The high-density, high-energy phenomena would require a relativistic and non-equilibrium kinetic theory at finite temperature. The relation between quasiparticle scattering amplitudes and Landau parameters is necessary for reasonable approximations and calculations for finite temperature properties of Fermi liquids [39] . Relativistic hadronic models are also essential to examine nuclear fissions and cluster radioactivities in terms of conservation laws and self-consistency [40] - [42] . Astrophysical problems such as the formation of neutron stars require finite temperature and nonlinear hadronic approximations [15] [16] [33] ; density and temperature inside stars will increase toward the center of a star, which is expected to produce pion condensations, hyperon generations and hadron-quark neutron stars [7] [8] [10] [31] .
It is important to know finite temperature effects on many-body systems of quasiparticles. Based on self-con- sistency and DFT, we extend the nonlinear (σ, ω) effective model to the finite temperature mean-field approximation and examine Landau parameters, finite temperature effects on Fermi liquid properties of nuclear matter.
2. Macroscopic Properties at Zero Temperature
The distribution function, 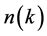 , is a function of quasiparticle momentum k and single particle energy
, is a function of quasiparticle momentum k and single particle energy 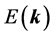 (0 ≤ k ≤ kF) directly connected to the ground state energy of Fermi particles at T = 0, and the single particle energy is equal to the chemical potential, μ0. The distribution function,
(0 ≤ k ≤ kF) directly connected to the ground state energy of Fermi particles at T = 0, and the single particle energy is equal to the chemical potential, μ0. The distribution function,  , has a characteristic property at T = 0: 1 (k ≤ μ0) and 0 (k > μ0), and physical quantities of the ground state of nuclear matter are described by the Fermi momentum, kF, or the baryon density,
, has a characteristic property at T = 0: 1 (k ≤ μ0) and 0 (k > μ0), and physical quantities of the ground state of nuclear matter are described by the Fermi momentum, kF, or the baryon density,  where ζ is a spin-isospin degeneracy number (ζ = 2 for neutron matter and ζ = 4 for nuclear matter).
where ζ is a spin-isospin degeneracy number (ζ = 2 for neutron matter and ζ = 4 for nuclear matter).
The current nonlinear  mean-field lagrangian is defined by:
mean-field lagrangian is defined by:
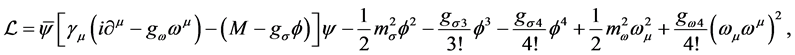 (1)
(1)
and meson quantum fields are replaced with classical fields: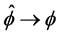 ,
, 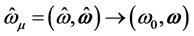 , (all Greek suffixes run as μ = 0, 1, 2, 3). The replacement of meson quantum fields by classical fields in mean-field lagrangians generally produces Hartree approximation [22] [23] [32] . Generalized nonlinear (σ, ω, ρ) mean-field approximations are discussed in [6] [33] and chap. 6 in [8] .
, (all Greek suffixes run as μ = 0, 1, 2, 3). The replacement of meson quantum fields by classical fields in mean-field lagrangians generally produces Hartree approximation [22] [23] [32] . Generalized nonlinear (σ, ω, ρ) mean-field approximations are discussed in [6] [33] and chap. 6 in [8] .
The hadron masses are chosen as M = 939, mσ = 550, mω = 783 MeV. The coupling constants are fixed so as to produce the nuclear matter saturation property: 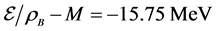 at kF = 1.30 fm−1. The saturation condition leads to the coupling constants: gσ = 9.298, gω = 10.660, gσ3 = 200.0 (MeV), gσ4 = 350.0, and gω4 = 350.0. These coupling constants yield, incompressibility K = 333.4 MeV and symmetry energy, a4 = 15.3 MeV. The maximum mass of neutron stars produced by the nonlinear model is
at kF = 1.30 fm−1. The saturation condition leads to the coupling constants: gσ = 9.298, gω = 10.660, gσ3 = 200.0 (MeV), gσ4 = 350.0, and gω4 = 350.0. These coupling constants yield, incompressibility K = 333.4 MeV and symmetry energy, a4 = 15.3 MeV. The maximum mass of neutron stars produced by the nonlinear model is 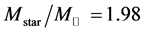 (
(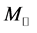 is the solar mass). In the following calculations, natural units are used:
is the solar mass). In the following calculations, natural units are used: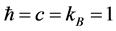 .
.
The equations of motion for the scalar and vector mesons are given by
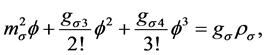 (2)
(2)
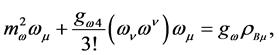 (3)
(3)
where 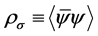

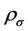
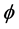
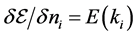
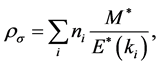
where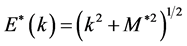
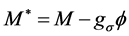
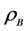
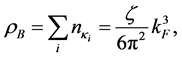
where ζ is a degeneracy factor: ζ = 4 for nuclear matter and ζ = 2 for neutron matter. The baryon current, jB, is similarly obtained from self-consistent condition as,
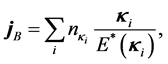
where the momentum 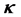
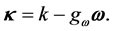
The single particle energy is given by Green’s function formalism, and the Fermi energy, 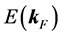
The Green’s function is defined by Schwinger-Dyson equation, and the baryon Green’s function with renormalized dynamical variables has a similar structure as the noninteracting Green’s function, which assumes the existence of the (on-shell) single quasiparticle energy,

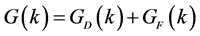

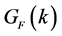
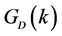
The energy density and pressure are calculated by way of energy-momentum tensor and Green’s function as [6] [8] [32] ,
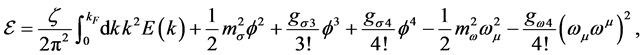
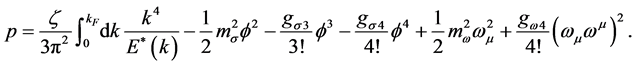
The matrix structure of the baryon self-energy will be reduced generally to the following form:
and so, we have three independent self-energy functions, 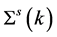
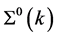
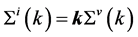
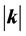
The self-consistent effective masses of hadrons should be determined from equations of motion, Green’s functions for baryons and mesons and the condition of self-consistency,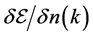
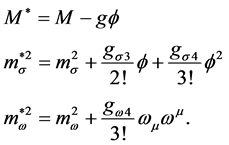
Scalar and vector self-energies are related to fields and sources by:
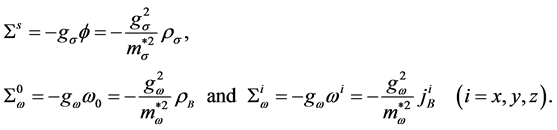
One should note that the effective masses (10) and self-energies (11) are derived from self-consistent condition, 
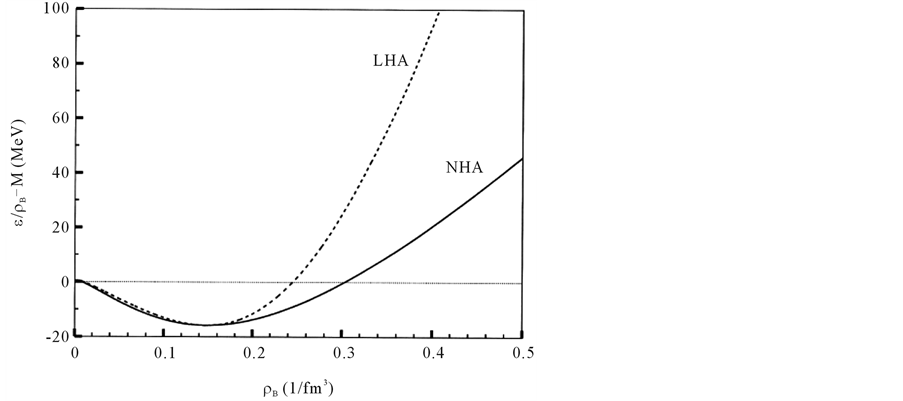
The saturation curves of binding energy at T = 0 are given in Figure 1, in order to show that the linear (σ, ω) and nonlinear (σ, ω) mean-field approximations in QHD model maintain the fundamental requirement of nuclear matter, which is taken in the current calculation as, ρB = 0.148 fm−3, 
Figure 1. Binding energies of symmetric nuclear matter at T = 0. The dotted-line is for LHA (linear σ, ω Hartree approximation), and solid-line is for NHA (nonlinear σ, ω Hartree approximation), which maintain the saturation condition: ρB = 0.148 fm−3,
(σ, ω) calculation usually produces a small value of symmetry energy, but it is improved by including ρ-meson, or extending to Hartree-Fock, Bruckner HF approximations [21] [32] [43] - [46] .
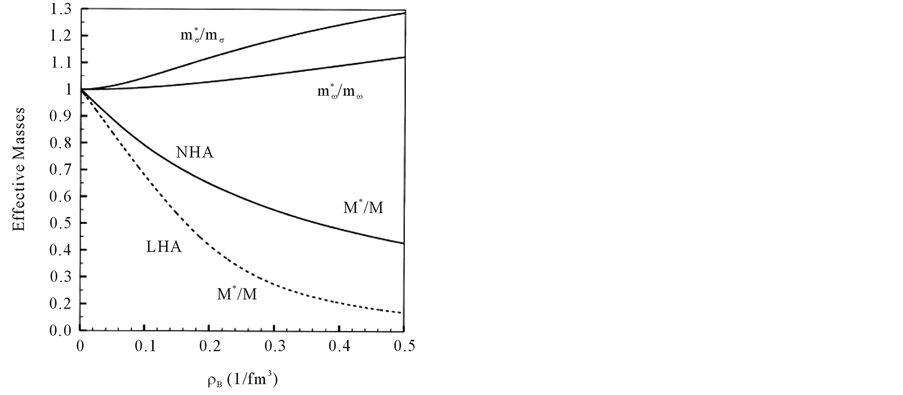
Effective masses of hadrons are shown in Figure 2. The effective mass of nucleon, 

3. Macroscopic Properties at Finite Temperature
To describe the system at finite temperature, we need a thermodynamic potential and partition function that will select the correct ground state in the limit T ® 0 [15] [16] . In the current calculations, the nonlinear (σ, ω) mean-field is reproduced at T ® 0. Thus, we are naturally directed to define

and the thermodynamic potential in our nonlinear (σ, ω) model is
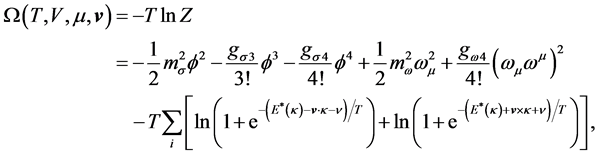
where 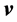
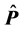
In finite temperature nuclear matter, particle anti-particle distribution functions are given by,
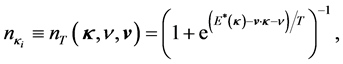

where the single particle energy is: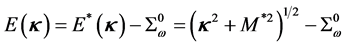

Figure 2. The effctive masses of nucleons and mesons in NHA (solid-lines) and LHA (dotted-line). The meson masses in LHA are constant: mσ and mω. The effective masses of mesons are produced by nonlinear interactions: 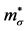
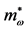
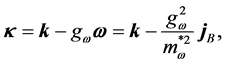
where 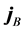
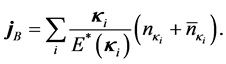
The self-consistency of nonlinear (σ, ω) approximation requires
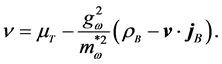
The chemical potential, 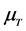
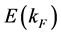

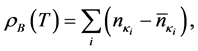
which is denoted as ρB for simplicity at finite temperature computations.
The equation of motion for scalar meson, which leads to the correct ground state in the limit T ® 0 and consistent with thermodynamic potential (13), is given by
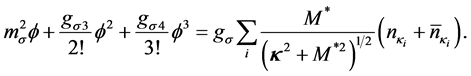
The scalar field, 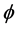
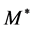

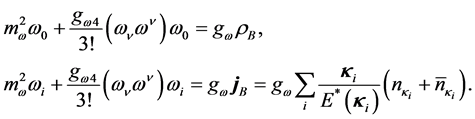
The energy density, pressure, entropy density and momentum density in the nonlinear (σ, ω) model are directly derived from the thermodynamic potential (13):
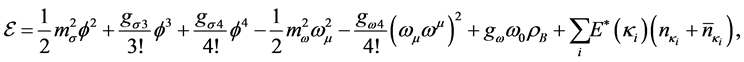
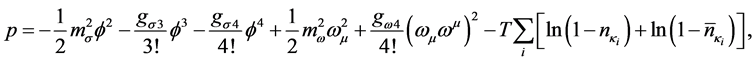


Note that the coupling constants are fixed so as to produce the nuclear matter saturation property: 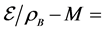
Though nonlinear coupling constants are introduced as free parameters to the model, the saturation conditions, self-consistency and density-dependent nonlinear interactions restrict the values of nonlinear coupling constants [6] [8] [10] . The restrictions to coupling constants become strict when spontaneous symmetry breaking mechanism is used to produce the chiral (σ, π, ω) mean-field model [8] [31] .
It is necessary to check whether or not generated physical quantities satisfy macroscopic conservation laws. Thermodynamic relations are discussed in the Ref. [15] [16] , and one can directly check the following fundamental thermodynamic relation, Gibbs’ relation, from the above equations,

and in the rest frame of nuclear matter, or a comoving frame defined by
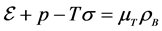
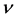
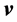
The concept of Fermi surface at finite temperature is introduced by the relation:
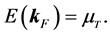
Equation (27) self-consistently determines the finite temperature Fermi-momentum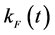
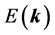

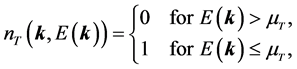
in the rest frame of nuclear matter with the limit of the baryon current,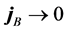
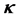
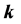
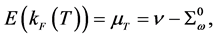
where 
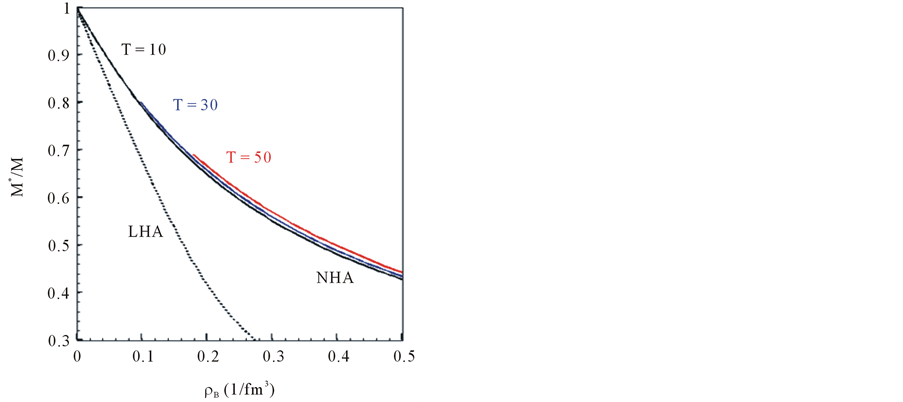
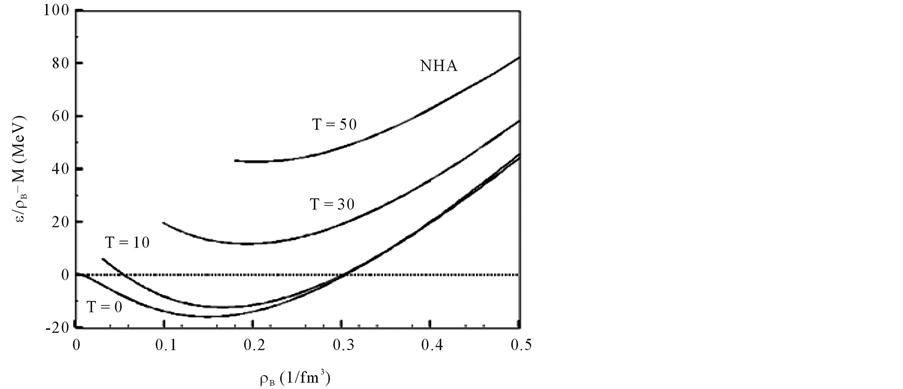
At a finite temperature and a low density, it is known that the sharp Fermi surface will be smoothed out, which is also perceived by the disappearance of solutions to Equation (27) at low densities. The stable ground state of Fermi-liquid at T = 0 is defined by a sharp Fermi energy defined by energy density, and the quasi-particle energy and Pauli exclusion principle are expressed simultaneously. In a finite temperature system, a sharp Fermi surface is smeared out by the effect of temperature agitation. Especially, Fermi energy at low density is completely smeared out and used, for example, to effective masses of hadrons and single particle energy, resulting in the increase of effective masses and binding energies shown in Figure 3 and Figure 4. These characteristics are consistent with those discussed in nonrelativistic calculations of 3He [27] .
The definition of Fermi surface is given by the condition, 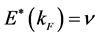
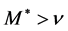
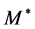
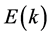
Figure 3. The effective masses of nucleons at finite temperatures: T = 0, T = 10, T = 30, T = 50 MeV. The results of T = 0 and T = 10 are similar.
Figure 4. The temperature effect on binding energy of symmetric nuclear matter. Solid-lines are solutions to Fermi-liquid sphere defined by (29). The onset of Fermi-liquid sphere is gradually shifting to a higher density with increasing temperature.
Fermi surfaces (the effective masses cannot be directly calculated because Fermi surface does not exist in the low densities: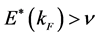
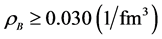
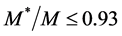
T = 10 MeV;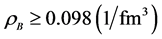
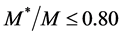
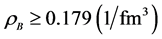
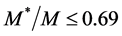
When baryon density is low, the Fermi surface is gradually smeared out and vanishes as temperature increases. With a fixed finite temperature, the Fermi energy (27) gradually becomes sharp as baryon density increases. The effect of temperature appears at low densities when the thermal energy exceeds Fermi energy and unfreezes the ground state energy of nuclear matter, indicating a gas-liquid phase transition of nuclear matter. The Fermi liquid analysis is confined in higher densities shown in nucleon effective masses and binding energies at 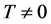
When the finite temperature Fermi-momentum 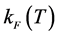
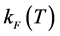
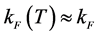

All discrete summations of physical quantities are changed to integrations taking care of spin-isospin degrees of freedom [32] . In order to compute thermodynamic functions, one needs to solve self-consistent equations for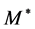
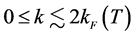
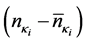
In Figure 3, effective masses are shown for T = 10, T = 30 and T = 50 MeV. The temperature effect is small on effective masses, and the result of T = 10 MeV is almost similar to the one at T = 0. However, the binding energy curves in Figure 4 indicate that the single particle energy at saturation density is relatively increased with temperature in the range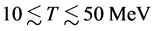
4. Landau Parameters at Finite Temperature
Landau’s theory of Fermi liquid is constructed so that quantum statistical properties, such as energy density, pressure, single particle energy and self-energies are consistent with macroscopic conservation laws, in other words, thermodynamic relations [4] [24] - [28] [34] - [36] . The requirement is not trivially true in an approximation, which is self-consistently related to Hamiltonian or Lagrangian formalism and approximation methods. The validity and applicability of Fermi-liquid theory are confined in the Fermi energy range, finite temperature and density which reasonably maintain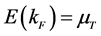
Based on the results in the sec. 3, Landau theory of nuclear matter can be rigorously discussed, since the current nonlinear (σ, ω) approximation maintains macroscopic conservation laws which can be rigorously proved with the fundamental relation, 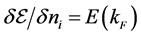
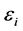
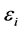
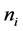
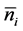
Landau parameters are self-consistently computed at the Fermi surface defined by (29):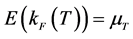
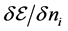
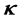
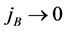

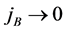
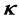
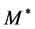
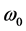
The quasiparticle energies are directly obtained from the functional derivative of the energy density, (22), with respect to quasiparticle distribution function of baryons and anti-baryons, 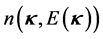
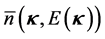
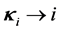
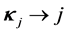
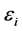

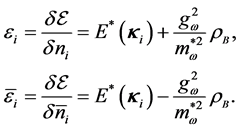
The functional derivatives of the quasiparticle energy with respect to baryon and antibaryon distribution functions will generate the baryon-baryon (NN), baryon-antibaryon (
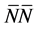
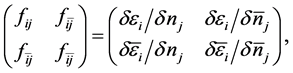
where
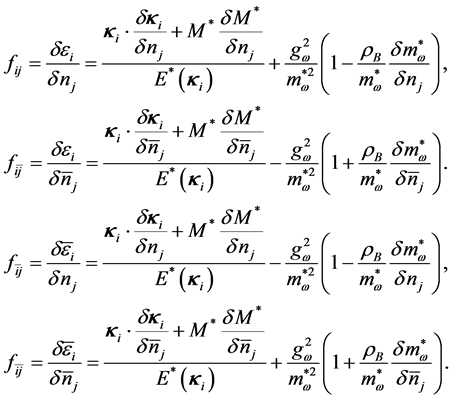
The closed forms of the coupled equations for the derivatives, 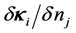

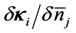

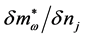
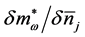
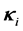
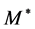
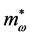

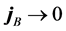
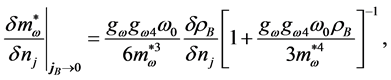
where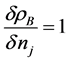
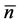
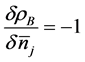
The functional derivatives of 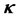
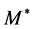

Since jB and 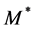
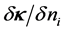
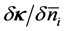
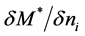

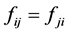
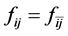
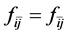
According to Landau’s theory of Fermi liquid [27] [28] , Landau parameters are defined by Legendre expansions of f's with respect to ki, kj, taken on the Fermi surface kF, and they are expressed as
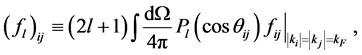
where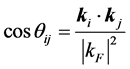
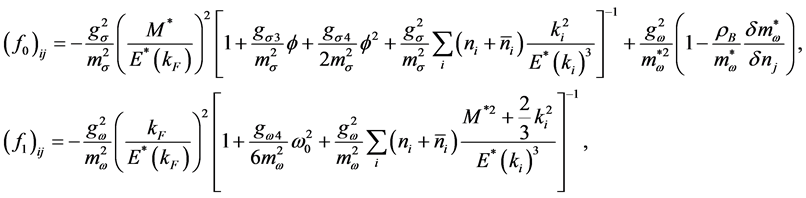
and 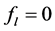
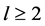
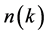

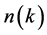
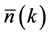
The relativistic density of states at the Fermi surface is defined by the use of δ-function as 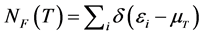
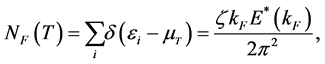
where ζ is the spin-isospin degeneracy factor: ζ = 2 for neutron matter, ζ = 4 for nuclear matter. The dimensionless Landau parameters are defined by
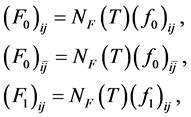
and the parameters, 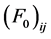
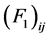
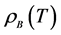
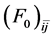
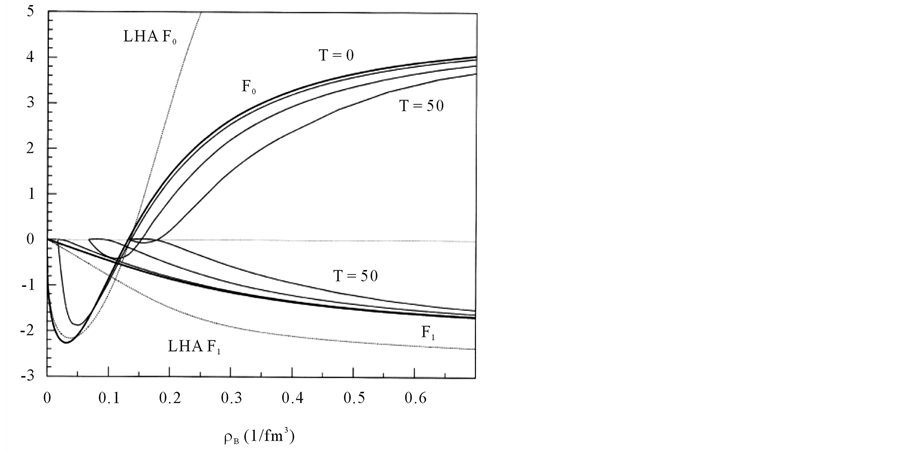
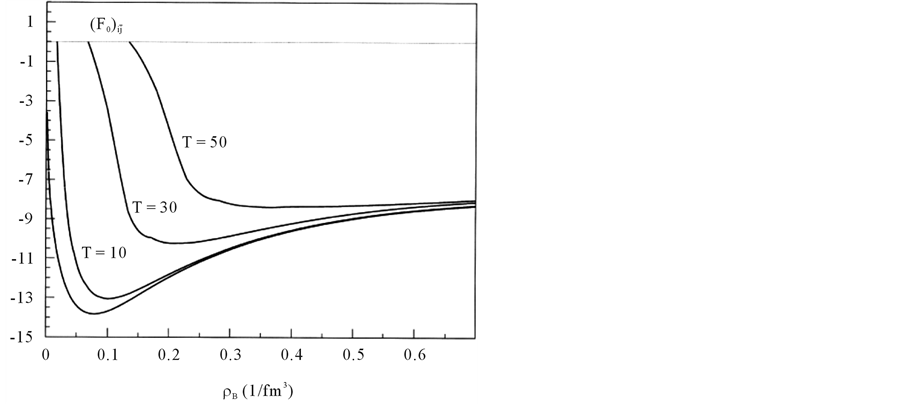
In the nonlinear (σ, ω) calculation, the values of Landau parameters, F0 and F1, become smaller compared to the linear (σ, ω) calculation (LHA). In addition, the finite temperature contribution shifts the density dependence of Landau parameters to a high density, resulting in the decrease of the magnitude of Landau parameters. The Figure 6 shows that baryon-antibaryon, (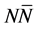

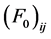
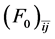
Figure 5. Landau parameters F0 and F1; LHA (dotted-line at T = 0) and NHA (solid-lines at T = 0, 10, 30, 50 MeV).
Figure 6. 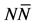
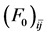
In the current finite temperature Fermi liquid calculation, there are only two components corresponding to baryon-baryon (NN) and baryon-antibaryon (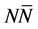
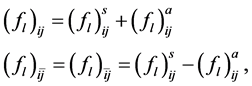
where 
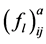
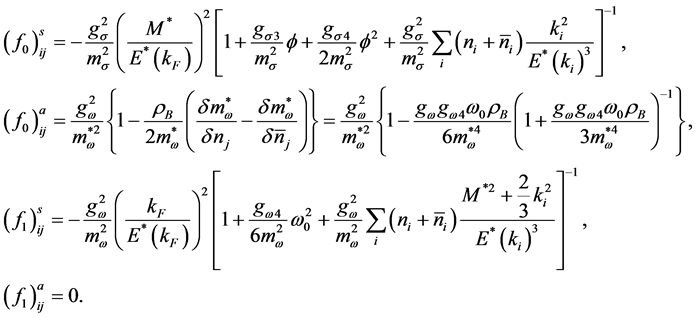
They are expanded in a series of Legendre polynomials as
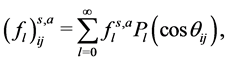
and the dimensionless symmetric and antisymmetric Landau parameters, 
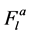

It is easy to see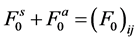
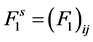


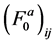
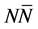
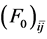
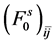
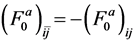
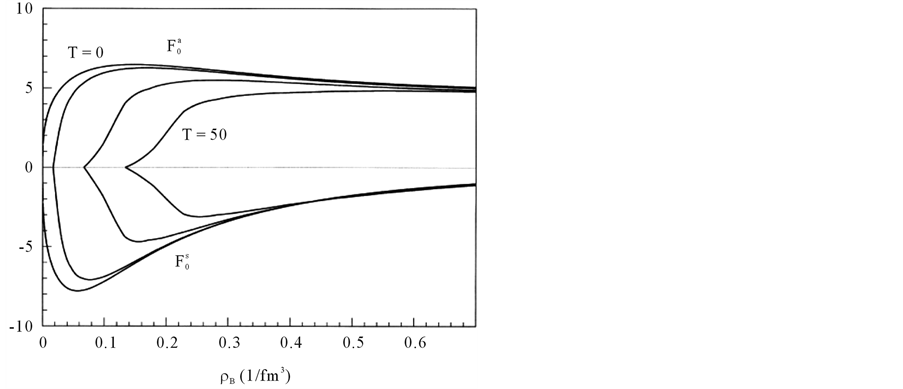
Figure 7. Symmetric and asymmetric Landau parameters, 

The attractive interaction coming from the exchange of scalar mesons exceeds the repulsive force due to the exchange of vector mesons at a low density; and the cancellation of large value of scalar and vector meson contributions can be observed in Figure 7 as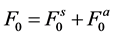
5. Macroscopic Properties and Scattering of Quasiparticles
Fermi-liquid properties, such as incompressibility, first sound velocity, symmetry energy and Landau parameters are discussed in a relativistic formalism [8] [45] [46] . The incompressibility, K, and symmetry energy, a4, are defined by (T = 0):
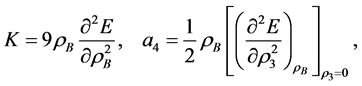
where the isovector, ρ3, is given by 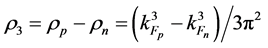
The first derivative of 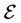
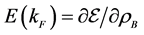
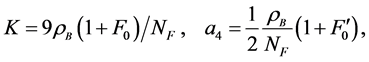
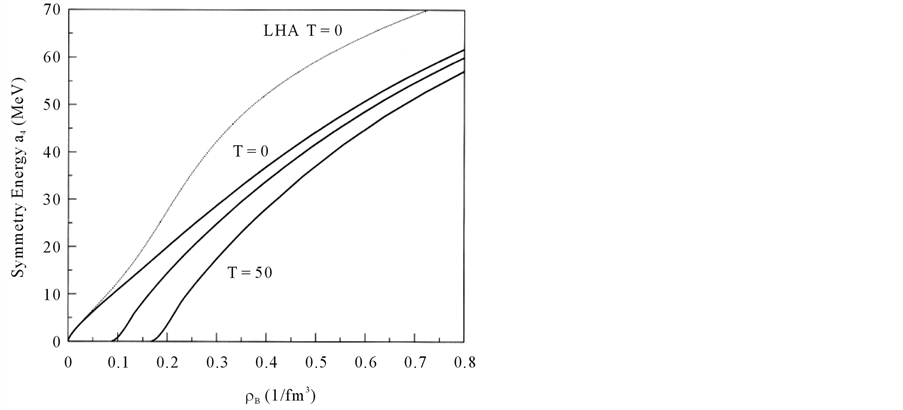
where the density of states, NF, baryon density, ρB, and Landau parameters are given in Sec. 3. In the current nonlinear (σ, ω) mean-field approximation, symmetry energy can be generally calculated as
which gives rather small value for a4. The Landau parameter, 
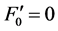
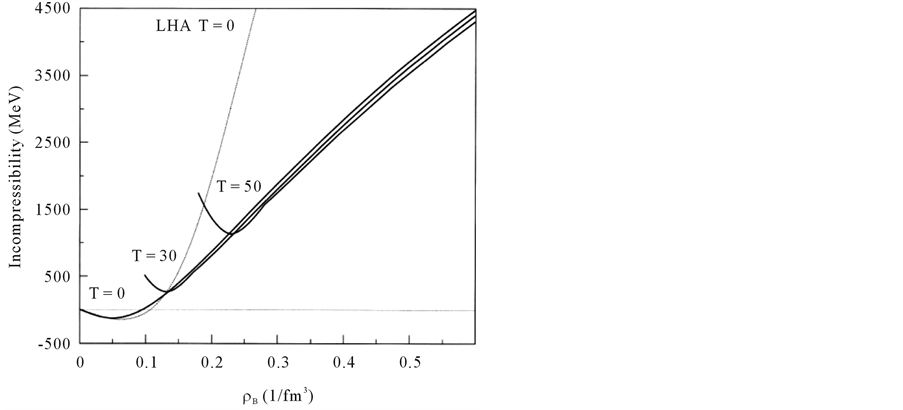
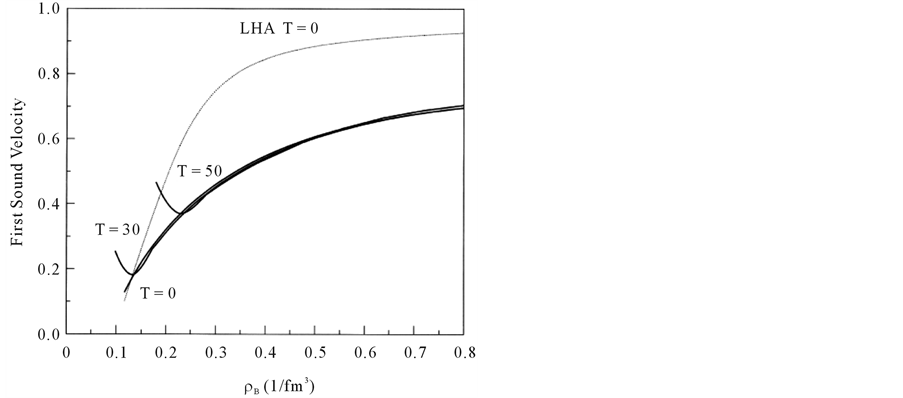
The incompressibilities, K, and symmetry energies, a4, for symmetric nuclear matter in the nonlinear (σ, ω) approximation at T = 0, T = 30, T = 50 are shown in Figure 8 and Figure 9 and compared to the result of the linear (σ, ω) mean-field approximation (LHA). The hydrodynamic first sound velocity C1 in the relativistic case is given by
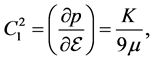
Figure 8. Incompressibilities of symmetric nuclear matter; LHA (dotted-line at T = 0) and NHA (solid-lines at T = 0, 30, 50 MeV. The Fermi ground states at low densities are shifted to a higher density according to binding energies in Figure 4.
Figure 9. Symmetry energies; LHA at T = 0 (dotted-line) and NHA (solid-lines at T = 0, 30, 50 MeV).
where p, 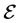
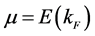
The Fermi-liquid properties are significantly reduced at high densities by nonlinear interactions. Because saturation curves are shifted to a higher density and energy (Figure 4), many-body properties such as incompressibility, symmetry energy and first sound velocity at saturation density are accordingly shifted to higher densities (Figure 8, Figure 9 and Figure 10), and it shows that the gas phase or gas-liquid type phase transition is also shifted to higher densities. These characteristic density-dependent properties at finite temperature should be checked experimentally.
Figure 10. First sound velocities; LHA (dotted-line) and NHA (solid-lines).
The quasiparticle scattering amplitude in the transport theory [26] [27] can be expressed in the current (σ, ω) nonlinear mean-field approximation. The transport equation for quasiparticles yields the equation for the scattering amplitude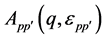
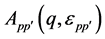
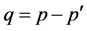

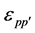
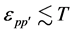
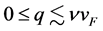
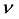
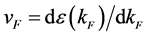
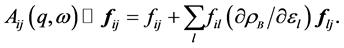
The expansions of Legendre polynomials in Equation (35) yield:
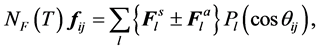
where

Properties of symmetric nuclear matter at saturation densities are listed. The saturation of the NHA (T ≥ 50) cannot be defined.
The transition probabilities of the quasiparticle collisions of baryon-baryon, baryon-antibaryon scattering, Wij and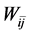
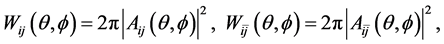
where 


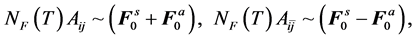
and the average transition probabilities are computed from the Equation (49) by employing Equation (50). Because of assumptions introduced to derive the equation for the scattering amplitude, the validity of Equation (48) should be confined in a density where constraints, 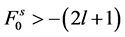

Table 1. Fermi-liquid properties for nuclear matter.
6. Concluding Remarks
The nonlinear (σ, ω) mean-field approximation is extended to finite temperature and applied to properties of nuclear matter by way of Landau’s Fermi-liquid theory. The finite temperature mean-field approximations in QHD are thermodynamically consistent relativistic approximations, and Landau’s assumption in the theory of Fermi liquid is maintained rigorously. Hence, nonlinear interactions of hadrons and finite temperature effects can be consistently examined in the mean-filed approximation of QHD.
The nonlinear interactions appear as density-dependent and energy-dependent interactions, which manifestly contribute at high densities. On the contrary, finite temperature effects appear at low densities of the Fermi-liq- uid ground state of nuclear matter and contribute to observables at saturation density. Although finite temperature effects on hadron effective masses are not large, the single particle energy 
At finite temperature, the Fermi surface is smeared out, which is observed by comparing Fermi momentums, 
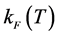
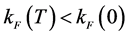
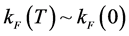
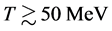
The Landau parameters in scattering amplitude, (48)-(50), should be checked in heavy-ion collision experiments, for instance, whether the modification to Fermi liquid properties or the reduction to Landau parameters is significant or not. Nucleon and meson effective masses depend on nonlinear and density interactions, which become noticeable above saturation densities. Hence, nonlinear and density modifications to physical quantities are important from saturation to higher densities, whereas finite temperature modifications would be important from low to saturation densities. From the current Hartree approximation, it is suggested that Fermi-liquid properties are fairly sensitive to variations of temperature at low densities.
Physical quantities sensitive to Landau parameters, 

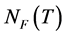
The exchange interaction in the Dirac-Hartree-Fock approximation in QHD is applied to obtain the value of Landau parameters [35] [36] . The similar analyses may be carried out in more sophisticated approximations in QHD, such as the effective chiral (σ, π, ω) mean-field [8] [31] approximation, the chiral (σ, π, ω) Hartee-Fock approximation [47] , and the chiral (σ, π, ω, ρ) model [48] . These analyses are necessary for applications to neutron stars as high density matter [6] - [8] , nuclear fission and cluster radioactivity [40] - [42] . It is important for the theory of finite temperature quantum liquids to examine heavy-ion collision experiments at a low temperature and a density, so as to clarify the validity and applicability of quasiparticle approach in nuclear matter.
Cite this paper
Schun T. Uechi,Hiroshi Uechi, (2016) Landau Theory of Fermi Liquid in a Relativistic Nonlinear (σ, ω) Model at Finite Temperature. Open Access Library Journal,03,1-18. doi: 10.4236/oalib.1102757
References
- 1. Walecka, J.D. (1974) A Theory of Highly Condensed Matter. Annals of Physics, 83, 491-529.
http://dx.doi.org/10.1016/0003-4916(74)90208-5 - 2. Haar, B. and Malfliet, R. (1987) Nucleons, Mesons and Deltas in Nuclear Matter a Relativistic Dirac-Brueckner Approach. Physics Reports, 149, 207-286.
http://dx.doi.org/10.1016/0370-1573(87)90085-8 - 3. Holinde, K. (1981) Two-Nucleon Forces and Nuclear Matter. Physics Reports, 68, 121-188.
http://dx.doi.org/10.1016/0370-1573(81)90188-5 - 4. Fetter, A.L. and Walecka, J.D. (2003) Quantum Theory of Many-Particle Systems. Dover Pub, New York.
- 5. Walecka, J.D. (1995) Theoretical Nuclear and Subnuclear Physics. Oxford University Press, New York.
- 6. Uechi, S.T. and Uechi, H. (2009) The Density-Dependent Correlations among Observables in Nuclear Matter and Hyperon-Rich Neutron Stars. Advances in High Energy, 2009, Article ID: 640919.
- 7. Serot, B.D. and Uechi, H. (1987) Neutron Stars in Relativistic Hadron-Quark Models. Annals of Physics, 179, 272-293.
http://dx.doi.org/10.1016/0003-4916(87)90137-0 - 8. Uechi, H., Uechi, S.T. and Serot, B.D. (2012) Neutron Stars: The Aspect of High Density Matter, Equations of State and Related Observables. Nova Science Pub, Hauppauge.
- 9. Jacob, M. and Thanh Van, J.T. (1982) Quark Matter Formation and Heavy Ion Collisions: A General Review and Status. Physics Reports, 88, 321-413.
http://dx.doi.org/10.1016/0370-1573(82)90083-7 - 10. Uechi, S.T. and Uechi, H. (2015) Hardon-Quark Hybrid Stars Constructed by the Nonlinear σ-ω-ρ Mean-Field Model and MIT-Bag Model. Open Access Library Journal, 2, e2012.
http://dx.doi.org/10.4236/oalib.1102012 - 11. Lourenco, O., Dura, M., Delfino, A. and Malheiro, M. (2011) Hadron-Quark Phase Transition in a Hadronic and Polyakov-Nambu-Jona Lasinio Models Perspective. Physical Review D, 84, Article ID: 125034.
http://dx.doi.org/10.1103/PhysRevD.84.125034 - 12. Weldon, H.A. (1982) Covariant Calculations at Finite Temperature: The Relativistic Plasma. Physical Review D, 26, 1394.
http://dx.doi.org/10.1103/PhysRevD.26.1394 - 13. Weldon, H.A. (1983) Simple Rules for Discontinuities in Finite-Temperature Field Theory. Physical Review D, 28, 2007.
- 14. Landsman, N.P. and Van Weert, Ch.G. (1987) Real- and Imaginary-Time Field Theory at Finite Temperature and Density. Physics Reports, 145, 141-249.
http://dx.doi.org/10.1016/0370-1573(87)90121-9 - 15. Furnstahl, R.J. and Serot, B.D. (1990) Covariant Mean-Field Calculations of Finite-Temperature Nuclear Matter. Physical Review C, 41, 262.
http://dx.doi.org/10.1103/PhysRevC.41.262 - 16. Furnstahl, R.J. and Serot, B.D. (1991) Covariant Feynman Rules at Finite Temperature: Time-Path Formulation. Physical Review C, 44, 2141-2174.
http://dx.doi.org/10.1103/PhysRevC.44.2141 - 17. Baym, G. and Kadanoff, L.P. (1961) Conservation Laws and Correlation Functions. Physical Review, 124, 287-299.
http://dx.doi.org/10.1103/PhysRev.124.287 - 18. Baym, G. (1962) Self-Consistent Approximations in Many-Body Systems. Physical Review, 127, 1391-1401.
http://dx.doi.org/10.1103/PhysRev.127.1391 - 19. Day, B.D. (1978) Current State of Nuclear Matter Calculations. Reviews of Modern Physics, 50, 495-521.
http://dx.doi.org/10.1103/RevModPhys.50.495 - 20. Hugenholtz, N.M. and Van Hove, L. (1958) A Theorem on the Single Particle Energy in a Fermi Gas with Interaction. Physica, 24, 363-376.
http://dx.doi.org/10.1016/S0031-8914(58)95281-9 - 21. Serot, B.D. (1992) Quantum Hadrodynamics. Reports on Progress in Physics, 55, 1855-1946.
http://dx.doi.org/10.1088/0034-4885/55/11/001 - 22. Uechi, H. (2001) Self-Consistent Structure in a Relativistic Dirac-Hartree-Fock Approximation. Nuclear Physics A, 696, 511-526.
http://dx.doi.org/10.1016/S0375-9474(01)01139-3 - 23. Uechi, H. (2004) The Theory of Conserving Approximations and the Density Functional Theory in Approximations for Nuclear Matter. Progress of Theoretical Physics, 111, 525-543.
http://dx.doi.org/10.1143/PTP.111.525 - 24. Migdal, A.B. (1968) Nuclear Theory: The Quasiparticle Method, W.A. Benjamin, Inc., New York.
Migdal, A.B. (1967) Theory of Finite Fermi Systems. John Wiley, New York. - 25. Petkov, I.Z. and Stoitsov, M.V. (1991) Nuclear Density Functional Theory. Oxford University Press, Oxford.
- 26. Baym, G. and Pethick, C. (1978) Landau Fermi-Liquid Theory and Low Temperature Properties of Normal Liquid 3He. In: Bennemann, K.H. and Ketterson, J.B., Eds., The Physics of Liquid and Solid Helium, Part 2, Wiley, New York, 1-122.
- 27. Pines, D. and Nozières, P. (1989) The Theory of Quantum Liquids. Vol. 1, Addison-Wesley, California.
- 28. Nozieres, P. (1997) Theory of Interacting Fermi Systems. Perseus Publishing, Cambridge.
- 29. Kohn, W. and Sham, L.J. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, A1133-A1138.
http://dx.doi.org/10.1103/physrev.140.a1133 - 30. Kohn, W. (1999) Nobel Lecture: Electronic Structure of Matter-Wave Functions and Density Functionals. Reviews of Modern Physics, 71, 1253-1266.
http://dx.doi.org/10.1103/RevModPhys.71.1253 - 31. Uechi, S.T. and Uechi, H. (2010) Density-Dependent Properties of Hadronic Matter in an Extended Chiral (σ, π, ω) Mean-Field Model. Open Access Library Journal, 2, 1-18.
- 32. Serot, B.D. and Walecka, J.D. (1986) Advances in Nuclear Physics. Edited by Negele, J.W. and Vogt, E., Vol. 16, Plenum, New York.
- 33. Müller, H. and Serot, B.D. (1995) Phase Transitions in Warm, Asymmetric Nuclear Matter. Physical Review C, 52, 2072-2091.
http://dx.doi.org/10.1103/PhysRevC.52.2072 - 34. Matsui, T. (1981) Fermi-Liquid Properties of Nuclear Matter in a Relativistic Mean-Field Theory. Nuclear Physics A, 370, 365-388.
http://dx.doi.org/10.1016/0375-9474(81)90103-2 - 35. Uechi, H. (1992) Landau Fermi-Liquid Theory and Approximations in the Quantum Hadrodynamical Model. Nuclear Physics A, 541, 397-412.
http://dx.doi.org/10.1016/0375-9474(92)90183-K - 36. Uechi, H. (1990) Constraints on the Self-Consistent Relativistic Fermi-Sea Particle Formalism in the Quantum Hadrodynamical Model. Physical Review C, 41, 744-752.
http://dx.doi.org/10.1103/PhysRevC.41.744 - 37. Uechi, H. (2008) Density-Dependent Correlations between Properties of Nuclear Matter and Neutron Stars in a Nonlinear σ-ω-ρ Mean-Field Approximation. Nuclear Physics A, 799, 181-209.
http://dx.doi.org/10.1016/j.nuclphysa.2007.11.003 - 38. Uechi, H. (2008) Correlations between Saturation Properties of Isospin Symmetric and Asymmetric Nuclear Matter in a Nonlinear σ-ω-ρ Mean-Field Approximation. Advanced Studies in Theoretical Physics, 2, 519-548.
- 39. Hakim, R. (2011) Introduction to Relativistic Statistical Mechanics, Classical and Quantum. World Scientific Publishing, Singapore.
- 40. Hooshyar, M.A., Reichstein, I. and Malik, F.B. (2005) Nuclear Fission and Cluster Radioactivity. Springer-Verlag, Berlin.
- 41. Krappe, H.J. and Pomorski, K. (2012) Theroy of Nuclear Fission. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-23515-3 - 42. Beck, C. Ed. (2014) Clusters in Nuclei. Volume 3, Springer-Verlag, Berlin.
- 43. Serot, B.D. (1979) A Relativistic Nuclear Field Theory with ∏ and ρ Mesons. Physics Letters B, 86, 146-150. (Erratum: Physics Letters B, 87, 403.)
http://dx.doi.org/10.1016/0370-2693(79)90804-9 - 44. Serot, B.D. and Walecka, J.D. (1979) Prop-erties of Finite Nuclei in a Relativistic Quantum Field Theory. Physics Letters B, 87, 172-176.
http://dx.doi.org/10.1016/0370-2693(79)90957-2 - 45. Uechi, H. (1989) Fermi-Liquid Properties of Nuclear Matter in a Dirac-Hartree-Fock Approximation. Nuclear Physics A, 501, 813-834.
http://dx.doi.org/10.1016/0375-9474(89)90162-0 - 46. Uechi, H. (2006) Properties of Nuclear and Neutron Matter in a Nonlinear σ-ω-ρ Mean-Field Approximation with Self-and Mixed-Interactions. Nuclear Physics A, 780, 247-273.
http://dx.doi.org/10.1016/j.nuclphysa.2006.10.015 - 47. Uechi, H. (2012) The Effective Chiral Model of Quantum Hadrodynamics Applied to Nuclear Matter and Neutron Stars. Journal of Applied Mathematics and Physics, 3, 114-123.
- 48. Serot, B.D. and Walecka, J.D. (1992) Chiral QHD with Vector Mesons. Acta Physica Polonica B, 23, 655-679.