Received 13 May 2016; accepted 18 July 2016; published 25 July 2016

ABSTRACT

In twenty-first century, automated stereoscopic warehouse has attracted many attentions of the enterprises because it has high working efficiency. The operation efficiency and management benefit of an automated stereoscopic warehouse are affected directly by the order picking efficient, it is an important symbol of service level about the automated stereoscopic warehouse. This paper from the perspective of the warehouse management to discuss the issue, the optimization assigned of location selection is regarded as the ultimate goal. A multi-objective mathematical model is established by setting “job efficiency” and “turnover rate” as objective functions, “warehouse space layout” as the constraint condition, and the genetic algorithm is used for coding this mathematical model which is applied to a pharmaceutical warehouse and solved by using Matlab software, result shows that the picking efficiency of normal temperature zone and the turnover of cargo area are have been greatly improved.

Keywords:

Automated Stereoscopic Warehouse, Optimization Assigned on Location Selection, Genetic Algorithm, The MATLAB Simulation

1. Introduction

Comparing with the ordinary warehouse, the automated warehouse has some advantages, such as low error rate of operation, high space utilization, and so on. The key factor of automated warehouse favored by enterprises is the high working efficiency. There are many factors that influence operation efficiency of the automated warehouse, which can be roughly divided into: mechanical equipment and warehouse management. Optimization assigned on location selection, belongs to the warehouse management problem, which is the focus of this paper.

2. Problem Description

2.1. Object of Study

Three key entities are selected as the research objects to analyze the problem of location optimization accurately, namely “cargo”, “cargo location” and “handling equipment”, the mathematical model is established to analyze the equilibrium relationship among cargo, cargo location and handling equipment, and finally we realize the goal of optimization assigned on location selection.

2.2. Fundamental Assumption

To make the mathematical model standardized, on the basis of objective reality, to the best solution oriented, the model assumptions are as follows:

(1) The storage unit is a pallet or container, goods stored in a single pallet or container is the same kind;

(2) All the size of the pallet or container are the same, and match with the cargo box, (the box size is the same), each cargo box, just can accommodate a pallet (or container).

(3) Shelves display are rectangular, the cargo box is a cube shape;

(4) In-out warehouse’s frequency of all types of cargo in the system will not change too much in a short time;

(5) The initial position of a stacker is located on the position which shelves closed to the entrance and exit;

(6) In the horizontal and vertical operations, the stacker speed value is a constant;

(7) The stacker can only save or take a cargo unit at a time;

(8) The goods can be directly complete stock pick without putting into warehouse;

2.3. Warehouse Layout Description

Automated stereoscopic warehouse has a total of A row of the shelf, each row has B column and C layer, one of the closest to the ground as the first layer, the nearest to entrance and exit as the first column, there is a stacker machine in each roadway, and a row of shelves on both sides of the roadway, a container (or pallet) on the shelf sides can be made accessing operation by a stacker.

3. Model Building

3.1. The Objective Function and Constraint Conditions

In the process of optimization assigned on location selection , this article selects two optimizing principles that are “nearest picking” principle based on in-out warehouse frequency and “first in first out” principle based on turnover rate, this paper establishes the specific optimization objectives which are “minimizing the total operation time” and “the total storage time of chosen goods is maximum”, combining with the constraint: warehouse space limitation, the “multi-objective mathematical model of optimization assigned on location selection” is built.

3.1.1. Objective Function S₁

The mathematical expression of objective function S₁considering minimum operation time is as shown below:

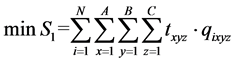(1)

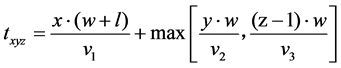(2)

S₁: expresses the sum picking time of goods waiting for out the warehouse;

T_xyz: expresses the outbound operating time of goods located at position (x, y, z);

q_ixyz: 0 - 1 decision variables;

i: the ith kind goods to be taken in the outbound order;

n_i: the ex-warehouse quantity of the ith kind goods;

N: the type number of goods in the outbound order;

(x, y, z): the position coordinates of goods waiting for picking;

(A, B, C): expresses the maximum number of row, column and layer of the shelves, respectively, those have a total of A row, B column, and C layer;

w: the length of the cube cargo box;

l: the roadway width;

V₁: the running speed of conveyor belt;

V₂: the mobile speed of a stacker in horizontal direction (Y direction);

V₃: the mobile speed of a stacker invertical;

3.1.2. The Objective Function S₂

The mathematical expression of the objective function S₂ based on the principle as follows:

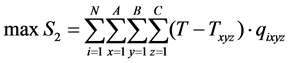(3)

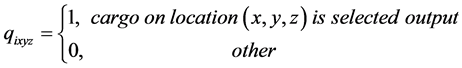(4)

S₂: indicates the sum storage time of selected goods;

T: indicates current time point of picking operation;

T_XYZ: indicates the storage time point of goods located at position (x, y, z).

3.1.3. Constraint Condition

1 ≤ x ≤ A; 1 ≤ y ≤ L; 1 ≤ z ≤ C, x, y and Z are all positive integers.

3.2. Multi-Objective Optimization Model

The multi-objective optimization model is shown.

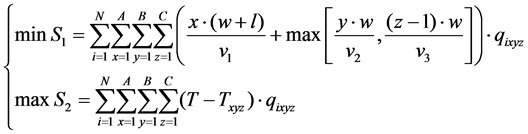(5)

4. Design of Model Algorithm Based on Genetic Algorithm

The optimization assigned on location selection s a problem that which locations cargo should be taken out to complete stock pick, ensure the highest operation efficiency and meet the rule “first in first out”.

4.1. Chromosome Coding Design

Coding problem, which is how to code the solution of problem becomes chromosome [1]. This article encodes the chromosome by adopting the binary coding method. Specifically, the chromosome gene site refers to the selected outbound goods, if a certain location was selected out of the warehouse, the corresponding gene value is 1, otherwise, the value is 0. The binary coding is a conclusive presentation, lacking specific description of the cargo information; therefore, it needs to use auxiliary string to describe the cargo information.

4.2. Fitness Function Setting and Genetic Operator Designing

4.2.1. Fitness Function Setting

In general, fitness function of genetic algorithm is the maximum problem, when it is not, it should be transformed at first [2].

The fitness function is designed to the value which the objective function S₂add the reciprocal of the objective function value S1 plus 1. The fitness function F (x, y, z) is expressed as:

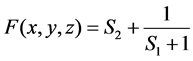(6)

4.3. Genetic Operator Design

(1) Selection operator design

It is selected the operator selection in this paper by using “the roulette wheel selection method”, Assuming the population number is N, and the fitness function value of individual i is Fi, the corresponding selection probability is P_i:

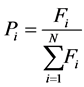(7)

Each round will produce a uniform random number between [0, 1] as a pointer to determine selected individual. The individual can be made the crossover operation after being selected.

(2) Crossover operator design

This paper chooses the way of “single point crossover”, namely selecting two individuals from the group to make interlace operation after selection operation and randomly generate a crossing point which the two individuals interchange parts genetic code, thus forming two new individuals.

(3) Mutation operator design

Mutation operation is to change the chromosome genevalue of each individual in the current group according to initial setting of the mutation probability [3] [4]. Based on the binary coding, this paper makes the gene value of chromosome code string to inverse operation and achieves the effect of variation, thus forming a new individual.

4.4. Design of Control Parameters and Algorithm Termination Conditions

In advance, some parameters are set in the algorithm run, “the control parameters”. In this article, the control parameters of the model are: population size M, termination evolution algebra T, crossover probability Pc, and mutation probability P_m. Among them, the population size refers to the individuals number contained in the group, the range is from 20 to 100; the termination evolution algebra of genetic algorithm, the range is 100 - 500; crossover probability P_C, the range is from 0.4 to 0.99; mutation probability P_M, the range is from 0.0001 to 0.1.

5. Case Verification and Result Analysis

5.1. Case Background

The storage area of an automated warehouse of a pharmaceutical company in Daxing Beijing Economic and Technological Development Zone including normal temperature area, easy odor area, cold storage area, special medicine area and so on.

5.2. Case Description

Two rows shelves area of the 1th roadway in normal temperature zone is selected as the analysis area, the region has 2*10*8 cargo locations.

The basic constant parameters of the handling equipment and shelves in the automated warehouse are as follow:

v₁ = 2 m/s, v₂ = 1 m/s, v₃ = 1 m/s.

A = 2, B = 10, C = 8, w = 1 m, l = 1.2 m.

The time how long it takes on putting in storage and other information about ten locations of drug 4 is seen in Table 1.

This article, firstly, solves assignment location model of one class cargo, gets the drugs chosen location assignment scheme and solves the rest class drugs waiting for out-warehouse by category, ultimately, acquiring picking operation list.

5.3. Model Solving Process

5.3.1. Model Deformation

This article considers the two goals are equally important and give equal weight, changes the second objective function into the reciprocal. The transformed single objective model is shown below:

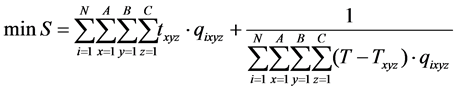(8)

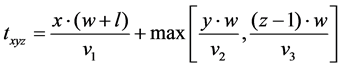(9)

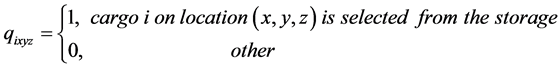
1 ≤ x ≤ 2, 1 ≤ y ≤ 10, 1 ≤ z ≤ 8, ∑q_ixyz = n_i.

5.3.2. Solution Process

Step 1: constructing chromosomes by using a binary encoding method;

Step 2: setting control parameters: population size NIND=20; crossover probability pc=0.8; mutation probability pm = 0.1; maximum genetic algebra MAXGEN=200;

Step 3: generating the initial population: Gen=1, randomly generating initial group Pop (0), including 160 individuals;

Step 4: if Gen > MAXGen, the algorithm meets the termination conditions, it stops, otherwise, it should be continue;

Step 5: calculating the objective function value according to the population of all chromosome information;

Step 6: calculating the fitness value of each individual;

Step 7: selecting individuals according to the fitness value size through the roulette method, then getting the next generation population by crossover and mutation operation;

Step 8: Gen = Gen + 1;

Step 9: go to Step 4.

5.4. Results Analysis

After running in the MATLAB software, the change curve of the objective function S can be derived, see Figure 1.

The curve change trend in the figure is showed that the objective function value is decreasing in the iteration process; the total operating time tends to be minimized, while the total storage time tends to be maximized. After 160 iterations, the fluctuation in the objective function value decreases and tends to be stable, and its value is S = 20.39. Therefore, the model is feasible.

After the end of the iteration, assignment result of the location selection is shown in Table 2.

It can be seen from the results of the table above, the selected operation location is located on the six cargo locations of column 6, 7, 8 in the first row and the second row.

From the above analysis, the assignment model of location selection can be solved by MATLAB software and obtain ideal location assignment strategy, meanwhile the model meets the requirements which the operation efficiency and turnover rate, so it has the feasibility.

6. Conclusions

In his article, using the multi-objective genetic algorithm theory and MATLAB software tool.

Selecting the pharmaceutical automation stereoscopic warehouse as research object, solving the chosen location assignment problem by optimization and simulation analysis, we confirm the built model is feasible. The model and the algorithm compiler have scientificity and certain reference value for the study of others related picking optimization problem, meanwhile it can provide a good decision-making basis for managers. In addition, the different conditions hypothesis of the model simplification will have different effects on the solution. This issue has not been discussed in this paper, which will be the focus of further research.

Acknowledgements

This work was supported by Beijing outstanding talent training project (2014000020124G093) and Beijing Intelligent Logistics System Collaborative Innovation Centre.

Cite this paper

Tongjuan Liu,Xiaoxia Ma,Xiaohui Zhan, (2016) Study of Optimization Assigned on Location Selection of an Automated Stereoscopic Warehouse Based on Genetic Algorithm. Open Journal of Social Sciences,04,52-58. doi: 10.4236/jss.2016.47008

References