Open Journal of Social Sciences
Vol.04 No.07(2016), Article ID:69369,9 pages
10.4236/jss.2016.47001
Dynamic Pricing for Perishable Products with Control of Cancellation Demands and Strategic Consumer
Hao Li, Meirong Tan, Liuxin Zou
School of Economics and Management, Chongqing Jiaotong University, Chongqing, China



Received 1 March 2016; accepted 18 July 2016; published 25 July 2016

ABSTRACT
In this paper, we consider the case that the consumers may cancel their reservations during the booking period so that consumers are divided into two parts: cancellation request and booking request. Simultaneously, we assume that consumers act strategically in booking products. Upon receiving the request, the firm has to decide whether to accept the cancellation request and what fees to charge the booking request in the presence of strategic consumers. We propose optimal price strategy and show the effectiveness of the decision models. We also obtain the optimal control of cancellation demands policy which is achieved by the number of remaining inventory. Numerical experiments are presented to explore the effect of various parameters on the performance of optimal strategy.
Keywords:
Control of Cancellation Demands, Revenue Management, Dynamic Pricing, Strategic Consumer

1. Introduction
In revenue management, the fundamental problem is the decision to find the optimal price or inventory level in order to maximize total revenue. However, even though a good decision is made, a perfect match between predicted inventory and realized inventory still cannot be guaranteed. If realized inventory exceeds predicted inventory, some inventory will lose its value after the sale period. On the other hand, some consumers will become lost sales. Generally, the gap between predicted inventory and realized inventory comes from cancellation demand. In such circumstances, cancellation cause damage to firm’s sale that extra capacity becomes available and could be used to accommodate other potential consumers, which makes the system more complicated to operate.
How could the firms to overcome this dilemma? Many organizations use the overbooking policy. Although this approach reduces the likelihood of being left with much unsold inventory, it may also lead to a difficult situation when the number of reservations exceeds the available inventory at the time of delivery. In such cases, the firm not only will lose the consumer but also damage the firm’s reputation. We present a possible business strategy in this paper. That is control of cancellation demand―whereby firm can decide whether or not accept a cancellation request in each period. The control of cancellation demands, combined with inventory vary dynamically, makes the determination of how best to gain revenue become a difficult problem in the firm’s decision systems: How could the firm to charge price for the consumer who wants to buy an item? If a cancellation request arrives, whether or not accept her request? The models contained in this paper will help to answer these questions.
Dynamic pricing models have been well studied in the literature. For reviews of pricing models for revenue management, please refer to Bitran and Caldentey (2003) [1], Levin and McGill (2009) [2] and Liu and Zhang (2013) [3], and for a survey of the literature that considers both pricing and inventory decisions, see Herk (1993) [4], Gallego and Van Ryzin (1994) [5], Elmaghraby and Keskinocak (2003) [6], Mahajan and Ryzin (2001) [7] and Kremer, Mantin, and Ovchinnikov (2015) [8]. In the stream of this work, a firm uses its price as a tool to induce demand, with the objective to maximize the total expected revenue when the sale ends. Because the optimal policy is often difficult to find analytically, in many cases the authors first establish structural properties of the optimal policy, and then develop an algorithm to compute or to approximate it. But these papers assume that consumers cannot cancel their reservations after purchasing.
There are a number of the microeconomic literatures in existence, which focus on cancellation. Karaesmen and Van Ryzin (2004) [9] develop a cancellation-based model that exploits two-stage stochastic programs. Other approaches include: experimental designs and multi-variate adaptive regression splines (Chen et al., 2003) [10] in a DP setting, a sampling-based approach that combines merits of mathematical programming and an approximate DP algorithm for networks in which cancellations and over bookings are permitted (see Bertsimas and Popescu, 2003) [11]. Also, Gosavi et al. (2005) [12] provide a model-free simulation based optimization approach that can account for a variety of system-related assumptions, including arbitrary distributions for demand-arrival processes and cancellations. Schütz and Kolisch (2013) [13] model the problem as a Markov decision process in discrete time which due to proper aggregation can be optimally solved with an iterative stochastic dynamic programming approach. As far as we know, the existing literatures on the revenue management problems have not fully addressed flexible control of cancellation demand yet.
The remainder of the paper is organized as follows. In the next two sections, we formulate our model and its associated dynamic programming value function. Section 4 analyzes the structure of the optimal policy and unfolds the basic property of the value function. A numerical example is presented in Section 5. We conclude with a brief discussion, as well as directions for future research in Section 6.
2. Model Descriptions
We assume that the supplier has 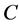 units of a perishable product at the beginning of the sales season. The booking horizon is divided into
units of a perishable product at the beginning of the sales season. The booking horizon is divided into 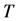 discrete time periods. The earliest period is period 0, and the last period is period
discrete time periods. The earliest period is period 0, and the last period is period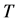 . We consider the case that the consumer may cancel their reservations during the booking period that extra capacity becomes available and could be used to accommodate other potential consumers. Based on the classification, there are two types of consumer: The first, we call it cancellation request, can be charged their service penalty, or they may be rejected. The second, we call it booking request, can be quoted prices that may vary dynamically. Also, we assume that these consumers are strategy. For strategic consumers, given price
. We consider the case that the consumer may cancel their reservations during the booking period that extra capacity becomes available and could be used to accommodate other potential consumers. Based on the classification, there are two types of consumer: The first, we call it cancellation request, can be charged their service penalty, or they may be rejected. The second, we call it booking request, can be quoted prices that may vary dynamically. Also, we assume that these consumers are strategy. For strategic consumers, given price 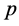 at time
at time , they rationally anticipate purchase opportunities at future, and will buy at
, they rationally anticipate purchase opportunities at future, and will buy at 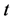 only if the price is more attractive. The arriving consumer purchases products at time
only if the price is more attractive. The arriving consumer purchases products at time 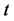 only if the consumer’s utility of buying products at present time is greater than in the future.
only if the consumer’s utility of buying products at present time is greater than in the future.
At any time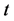 , the firm has to make the following decisions:
, the firm has to make the following decisions:
1) Accept or reject a cancellation request when a cancellation request arrives.
2) Charge fees of the booking request in the presence of strategic consumers.
The supplier maximizes the expected revenue by simultaneously determining whether or not accept the cancellation request and the optimal prices for booking request in the presence of strategic consumers at any given time and remaining inventory. Figure 1 displays the decision procedure.
The following notation is used throughout the paper:
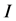 : the number of remaining inventory;
: the number of remaining inventory;
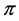 : the refund per cancellation;
: the refund per cancellation;
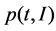 : price of a product in period
: price of a product in period 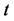 (simply denoted
(simply denoted 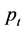 or
or );
);
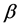 : degree of strategic behavior of the consumer,
: degree of strategic behavior of the consumer,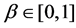 .
.





Figure 1. Two types of requests and the decision procedure.






















Let us formally make some assumption for our model.
1) In each time-period



2) The refund per cancellation, 
3) The cumulative probability distribution of the reservation price of a booking request, 
3. The Model
Given price 


The boundary conditions of Equation (1) are:
1)
2)
In Equation (1), 

We can solve the maximize of 







where 

Then, in any period

Let

For each 


where

The boundary conditions of Equation (3) are:
1)
2)
Denote:


A natural question arises as to whether or not our model is better than the traditional revenue management model without control of cancellation demands. First, we know that the traditional revenue management model with cancellation demands is defined as follow, which mean that the firm always accepts the cancellation request in each period when cancellation demands arrives:

If the firm always rejects the cancellation request in each period when cancellation demands arrives, the expected revenue can be expressed as

That is, for all 



Theorem 1. The control of cancellation demands model in Equation (3) performs no worse than the non- control of cancellation demands model in Equation (6) and Equation (7), i.e., for any 



Proof. We can prove this theorem by induction.
1) Clearly, 






where the first inequality follows by
2) Similar to case 1), we can prove that for any




where the first inequality follows by
This completes the proof of this theorem.
4. The Structure of Optimal Policies
To derive the optimal policy, we begin with a marginal analysis of inventory. We first study the optimal value function
Lemma 1. (1) For any fixed


(2) For any fixed


This lemma shows that more stork and/or time leads to higher expected revenues.
In the sequel, we use the following notations for the quantities marginal in




request at state






Lemma 2. For any fixed




Proof. 1) Let


But the expression on the right-hand side is positive, which is a contradiction.
2) Let
This completes the proof.
Several revenue management models, such as Gallego and Van Ryzin (1994) [5], have shown that 


Theorem 2. 


Proof. Let
For any fixed
because 

So we have
The proof is by inverse induction on time. The basis for induction is the terminal conditions. When
We can see that 



Then:
Obviously, the expression on the right-hand side of 





This completes the proof.
Theorem 3. The optimal price satisfies the equation:

Furthermore, if 


Proof. Taking the first derivative of 



The second derivative of 

From Equation (9), we have:
Because 

We have
So if 


This completes the proof.
Although Theorem 3 gives the sufficient condition for the optimal price, obtaining it in closed form is quite difficult. However, we can make a number of qualitative statements about the optimal prices. We summarize these in the following theorem.
Corollary 1. 


Proof. By theorem 2, we know that
Then, we have 





According to Corollary 1, at a given point in time, the optimal price drops as the inventory increases. This property is useful if one wants to compute the optimal price policy numerically because they significantly reduce the set of prices over which one needs to optimize.
Under additional assumptions on



Corollary 2. 


Proof. Similar to Corollary 1, from the theorem 2 and Lemma 1, we can obtain the conclusion.
From Equation (3) we know, a booking request for the first type of consumers is accepted if and only if
Theorem 4. Let:
1)

2)
if
Then, the firm accepts a cancellation request if and only if the number of selling units is
Proof. If
and
It implies that for

If

Thus, when



This completes the proof.
The following corollary immediately follows from the optimal capacity control policy described in the above theorem.
Corollary 3. The optimal threshold level for the cancellation request, 

Proof. We prove it by contradiction. Suppose that








Because
This contradicts the definition of
Corollary 3 demonstrates that the higher the refund is, the lower 
Now we present a computation procedure for the optimal policy. The procedure leads to a closed-form solution which satisfies Equation (3). Moreover, as part of the control rules, all thresholds and price are jointly determined. We describe the recursive solution process as follows.
First, we note 












5. Numerical Experiments
We present a numerical experiment in this section to illustrate how the proposed approach works in a constructed example.
We tested sets of examples with







First, we will illustrate the refund value 









Next, we consider the ratio of expected total revenue. The ratio is shown in Figure 3 as a function of 



Figure 2. The optimal control threshold 


Figure 3. The value of 


We can see that if the probability of cancellation request is increasing, the value of 



6. Conclusions
In this paper we research the control policy of cancellation demands in revenue management. By building multi- period dynamic programming model, we obtained the price relation which meet to strategic consumers. In addition, we proved that the firms optimal revenue function and structure properties of pricing strategy. Finally, we use numerical experiments to explore the effect of various parameters on the performance of optimal strategy and show the effectiveness of the decision models. The results show that:
1) When the probability of cancellation request is large, there will be fewer cancellation inventory retained for those consumers in order to gain more profit trough dynamic pricing.
2) The control of cancellation demands model is no worse than the non-control of cancellation demands model with different type of I.
Our research can provide theoretical basis for the optimal pricing decision to firms in control of cancellation demands. There are a number of important research avenues that can be pursued. How to decide the refund per cancellation? In this paper, we only take strategic consumer into booking products, we can explore the normal purchase in the presence of strategic consumers in the future.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No: 71402012), and the Natural Science Foundation of Education in Chongqing(KJ130402).
Cite this paper
Hao Li,Meirong Tan,Liuxin Zou, (2016) Dynamic Pricing for Perishable Products with Control of Cancellation Demands and Strategic Consumer. Open Journal of Social Sciences,04,1-9. doi: 10.4236/jss.2016.47001
References
- 1. Bitran, G. and Caldentey, R. (2003) An Overview of Pricing Models for Revenue Management. Manufacturing & Ser-vice Operations Management, 5, 203-229. http://dx.doi.org/10.1287/msom.5.3.203.16031
- 2. Levin, Y. and McGill, J. (2009) Dynamic Pricing in the Presence of Strategic Consumers and Oligopolistic Competition. Management Science, 55, 32-46. http://dx.doi.org/10.1287/mnsc.1080.0936
- 3. Liu, Q. and Zhang, D. (2013) Dynamic Pricing Competition with Strategic Customers under Vertical Product Differentiiation. Management Science, 59, 84-101. http://dx.doi.org/10.1287/mnsc.1120.1564
- 4. Herk, L. (1993) Consumer Choice and Cournot Behavior in Capaci-ty-Constrained Duopoly Competition. Rand Journal of Economics, 24, 399-417. http://dx.doi.org/10.2307/2555965
- 5. Gallego, G. and Van Ryzin, G.J. (1994) Optimal Dynamic Pricing of Invento-ries with Stochastic Demand over Finite Horizons. Management Science, 40, 999-1020. http://dx.doi.org/10.1287/mnsc.40.8.999
- 6. Elmaghraby, W. and Keskinocak, P. (2003) Dynamic Pricing in the Presence of Inventory Considerations: Research Overview, Current Practices, and Future Directions. Management Science, 49, 1287-1309. http://dx.doi.org/10.1287/mnsc.49.10.1287.17315
- 7. Mahajan, S. and Van Ryzin, G. (2001) Inventory Competition under Dynamic Consumer Choice. Operations Research, 49, 646-657. http://dx.doi.org/10.1287/opre.49.5.646.10603
- 8. Kremer, M., Mantin, B. and Ovchinnikov, A. (2015) Dynamic Pricing in the Presence of Strategic Consumers: Theory and Experiment. Social Science Electronic Publish-ing.
- 9. Karaesmen, I. and van Ryzin, G. (2004) Overbooking with Substitutable Inventory Classes. Operation Re-search, 52, 83-104. http://dx.doi.org/10.1287/opre.1030.0079
- 10. Chen, V., Gunther, D. and Johnson, E. (2003) Solving for an Optimal Airline Yield Management Policy via Statistical Learning. Journal of the Royal Statistical Society Series C, 52, 19-30. http://dx.doi.org/10.1111/1467-9876.00386
- 11. Bertsimas, D. and Popescu, I. (2003) Revenue Management in a Dynamic Network Environment. Transp Sci, 37, 257- 277. http://dx.doi.org/10.1287/trsc.37.3.257.16047
- 12. Gosavi, A., Ozkaya, E. and Kahraman, A.F. (2006) Simulation Op-timization for Revenue Management of Airlines with Cancellations and Overbooking. Operations Research, 29, 21-38. http://dx.doi.org/10.1007/s00291-005-0018-z
- 13. Schütz, H.-J. and Kolisch, R. (2013) Capacity Allocation for Demand of Different Customer-Product Combinations with Cancellations, No-Shows, and Overbooking When There Is a Sequential Delivery of Service. Annul Operations Research, 206, 401-423. http://dx.doi.org/10.1007/s10479-013-1324-5




























