Open Access Library Journal
Vol.03 No.06(2016), Article ID:69345,6 pages
10.4236/oalib.1102678
An Extended Newtonian Theory for Gravitational Bound Systems
Barbaro Quintero-Leyva
Independent Work, Miami, FL, USA

Copyright © 2016 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 May 2016; accepted 10 June 2016; published 13 June 2016

ABSTRACT
A physical fundament was derived to support the empirical correction to the balance between the force given by Newton 2nd law and Newton gravitation introduced previously by the author to account for the perihelion precession of Mercury. An equation was obtained that coincided in sign and magnitude with the Einstein perihelion shift when the 3rd law of Kepler was used to express the orbital period in term of the semi-major axis and the same level of accuracy was demanded. Other more accurate equations for the intrinsic perihelion shift were obtained that resulted in a relative deviation of about 1% or less.
Keywords:
Celestial Mechanics, Newtonian Gravitation, Newton’s 2nd Law, Theory of Relativity, Perihelion Precession, Cosmology
Subject Areas: Applied Physics, Classical Physics, Modern Physics, Special Theory of Relativity, Theoretical Physics

1. Introduction
Alternative theories to the Einstein General Theory of Relativity (GTR) that fully account for the intrinsic (two- body problem) perihelion precession of Mercury can be found in the literature. Few examples are: The development of a modified relativistic theory of gravitation with focus on the Mach’s principle [1] ; The generalization of the Einstein Special Theory of Relativity (STR) to an acceleration field [2] ; The Maxwellian Gravity theory, where use is made of gravitational Lienard-Wiechert potential and gravitational Thomas precession in the relativistic version of Maxwell-Heaviside’s toy model vector theory of gravity [3] ; The use of the momentum conservation law, the relativistic variation of mass and the relativistic variation of time (using the gravitational redshift factor) as the components of the total precession [4] .
The present work derives a fundament to the empirical correction to the balance between the force given by Newton 2nd law and Newton gravitation introduced previously by the author to account for the intrinsic perihelion precession of Mercury. An equation is obtained that coincided in sign and magnitude with the Einstein perihelion shift for the same level of accuracy. Also more accurate equations for the perihelion shift are obtained that result in a relative deviation of about 1% or less.
The fundament introduced in this work is based on the concept of Newtonian acceleration, length contraction and time dilation and it results in an acceleration equation which differs from the Newtonian one by just a power of the ubiquitous Lorentz factor. Because of this, the equation of motion is very simple and can have a beneficial impact on the computational efficiency of, for example, relativistic many-body problems.
The motivation of this paper is to provide a physical fundament to the results empirically obtained in reference [5] , to make a correction to the sign of the perihelion shift equation reported in [6] and to show that proper equations for the intrinsic perihelion shift can be obtained using the extended Newtonian theory presented here.
2. Extended Newtonian Theory for Gravitational Bound Systems
The one dimensional Newtonian acceleration for an observer at rest with the ‘fixed stars’ can be expressed as
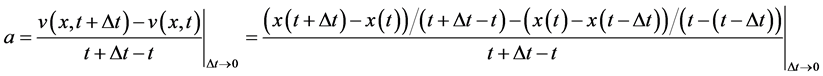
which it can be written as
 (1)
(1)
Note that it is assumed that the space and time length do not depend on the relative velocity of the observers and that the time flows at the same rate always while the space displacement depends intrinsically on the speed-time profile of the moving body.
The Newtonian force is then written as
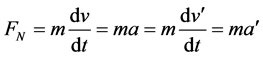
where the prime indicates an observer at rest with the moving body.
If the concept of “fixed stars” is not good enough one can always refer it to the center of the Galaxy, Cluster, or of the Universe in question.
The Michelson-Morley experiment result along with the Lorentz-Fitzgerald transformation, and Einstein special theory of relativity support the concept of the apparent time dilation and length contraction given by
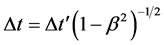 . Time dilation
. Time dilation , v is the speed of the moving reference frame and c is the speed of light in vacuum and
, v is the speed of the moving reference frame and c is the speed of light in vacuum and 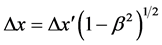 length contraction.
length contraction.
Substituting those relations into Equation (1),
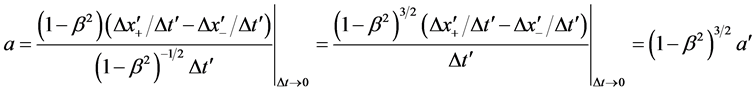
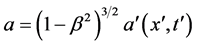
So the force measured in a frame at rest with the “fixed stars” can be written as:
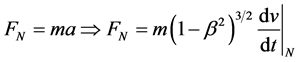
Note that here it was used 3 space-time points with one space-time interval contraction/dilation (one interval boost). However the concept of acceleration requires 2 space-time intervals contraction/dilation (two successive-interval boosts) to relate the 3 space-time points in question.
Considering another reference frame moving with a velocity v with respect to the prime reference frame, the following is written (two successive interval boosts):

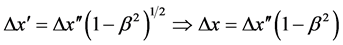
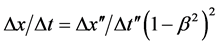
Substitute into Equation (1):
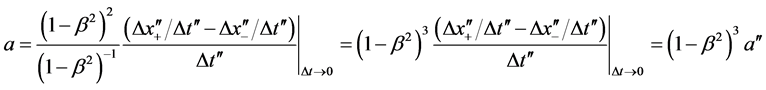
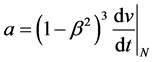 (2)
(2)
So the force measured in a frame at rest with the “fixed stars” is written as:

The Newtonian acceleration (Equation (1)) in 3 dimensions is written as

In gravitational bound systems where the moving object is revolving around a very massive body or around the center of mass of the system, the direction of the moving body in question is continuously changing, it is assumed then that the length contraction happens in the 3 Cartesian directions, and assuming that the speed of the gravitational interaction is the same as the speed of light in vacuum, the following holds for two successive interval boosts:






When the above equations are substituted into Equation (3), Equation (2) is reproduced.
Note that Equation (2) was obtained assuming that the body of interest was initially at rest, if the body were initially moving and slowing down to a rest state, one could think that the exponent of the multiplier of the Newtonian acceleration should be −3 instead of +3 which could suggest that the sign of the exponent depends on the local (Newtonian) acceleration. However when this dependence was implemented in the numerical solution of the time-dependent two-body problem, no significant perihelion shift was obtained for Mercury. This suggests that the sign of the exponent could be an indication of a separate effect (e.g. the expansion/contraction of the system in question: star systems (e.g. solar system, birth/explosion and death/implosion of stars), galaxies (e.g. Milky way), the universe in question (ours), etc.).
It could be worthy as mentioned before in [6] to perform experiment to determine n from 
3. The Intrinsic Perihelion Precession
The balance between the force given by Newton’s 2nd law and the Newtonian gravitation in polar coordinates using −3 (instead of +3) as the exponent of the multiplier of the Newtonian acceleration (Equation (2)) was obtained in reference [6] for the solar system, that Equation generalized for an arbitrary exponent is written as



The solution of Equation (4), noting that the multiplier of b represents a small perturbation, is expressed in terms of a Fourier series as [7]

From which the following equations are obtained:


Neglecting the terms containing 2nd and higher power of 





For n = −3,

It is notified that Dr. Roy [8] called my attention on that in reference [6] , the sign in front of 
Substituting into Equation (4) and comparing coefficients of


The angle between two succeeding perihelion is written as:

The precession of the perihelion per revolution is:

The precession of the perihelion per orbital period is 

The Einstein GTR result of the precession per revolution is given by [9] 

In reference [6] it is reported that the absolute value of Equation (7) is the same as that of the Equation (8) when the orbital period is expressed in terms of the semi-major axis through the 3rd Kepler law. So 
For n = +3,

Substituting it into Equation4, passing the denominator of Equation (5g) to the left-hand side, neglecting the terms containing 2nd and higher power of

Substituting the expression for



Making the substitution 
As A is much smaller than B and C and the root of interest is close to 1 the quartic term is dropped to get:

Neglecting the 1st term in the numerator and the 2nd term in the denominator:

Using series expansion

Then the perihelion shift based on Equation (12) is 
It is noted that when Equation (11) is substituted back into Equation (9) for verification, the left-hand side becomes zero if the terms containing 2nd and higher power of 

Mercury perihelion shift using MS Excel, results in 48.57634, 43.20905, and 42.98185 for calculations based on Equations (9), (10) and (12) respectively.
Due to the very small value of the A coefficient it was suspected that the results based on the quartic equation could be affected by the number of precision-digits used in MS Excel 2010. Table 1 shows the perihelion shift
Table 1. Intrinsic Mercury perihelion precession in arcsec/century.
for Mercury using the different approximations described here. The 1st column is the number of precision-digits set in the code editor of Maple 18. The other columns show the results of the perihelion shift based on the indicated equation number. From that table it can be seen that when the perihelion shift calculation is based on the quartic approximation (Equation (9)) it is needed about 20 precision-digits to obtain reliable results however the quadratic equations yield accurate results for even 10 digits. Note that the difference between the results based on Equation (12) and the one based on Equation (9) is about 0.45 “/cy (~1% relative deviation) while with respect to the results based on Equation (10) the difference is about 0.23 “/cy (0.5%).
The values of 

4. Summary
A fundament is derived to support an empirical correction to the balance between the force given by Newton 2nd law and Newton gravitation introduced previously. The fundament is based on the concept of Newtonian acceleration, length contraction and time dilation, and it results in an acceleration equation which differs from the Newtonian one by just a power of the ubiquitous Lorentz factor.
An equation is obtained (from the polar coordinate-equation of motion) that coincides in sign and magnitude with the Einstein perihelion shift when the 3rd law of Kepler is used to expressed the orbital period in term of the semi-major axis and the same level of accuracy is demanded.
Other more accurate equations for the intrinsic-perihelion shift are obtained that result in a relative deviation of about 1% or less.
Acknowledgements
I would like to thank Dr. M. Krizek for his valuable comments and suggestions.
Cite this paper
Barbaro Quintero-Leyva, (2016) An Extended Newtonian Theory for Gravitational Bound Systems. Open Access Library Journal,03,1-6. doi: 10.4236/oalib.1102678
References
- 1. Brans, C. and Dicke, R.H. (1961) Mach’s Principle and a Relativistic Theory of Gravitation. Physical Review, 124, 925.
http://dx.doi.org/10.1103/PhysRev.124.925 - 2. Note, M. (1985) The Special Theory of Relativity in a Gravitational Field. International Journal of Fusion Energy, 3.
- 3. Behera, H. and Naik, P.C. (2003) A Flat Space-Time Relativistic Explanation for the Perihelion Advance of Mercury. arXiv:astro-ph/036611v1.
- 4. Biswas, A. and Mani, K.R.S. (2005) Simulation Model for Anomalous Precession of the Perihelion of Mercury’s Orbit. CEJP, 3, 69-76.
http://dx.doi.org/10.2478/bf02476507 - 5. Quintero-Leyva, B. (2015) On the Intrinsic Precession of the Perihelion of Mercury. Open Access Library Journal, 2, e2239.
http://dx.doi.org/10.4236/oalib.1102239 - 6. Quintero-Leyva, B. (2016) On the Intrinsic Precession of the Planets of the Solar System. Open Access Library Journal, 3, e2554.
http://dx.doi.org/10.4236/oalib.1102554 - 7. Bergmann, P.G. (1976) Introduction to the Theory of Relativity. Dover Publications, Inc., New York.
- 8. Roy, R. (2016) Personal Communication. Department of Electronics and Electrical Communication Engineering, Indian Institute of Technology, Kharagpur, India.
- 9. Einstein, A. (1916) The Foundation of the Generalized Theory of Relativity (Die Grundlage der allgemeinen Relativitatstheorie). Annalen der Physik, 354, 769-822.
http://dx.doi.org/10.1002/andp.19163540702










