Received 26 April 2016; accepted 13 May 2016; published 17 May 2016

ABSTRACT

The paper discusses two cases showing crucial effects of error correction. It proves that contrary to the common belief, the electronic state of atoms having more than one electron has a multiconfiguration structure and that the central field approximation provides an inadequate description of the wave function. Fundamental isospin properties prove that baryonic quarks (like those of the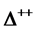) can be regarded as ordinary Dirac particles. Theoretical consequences of these issues are discussed.

Keywords:

Atomic Wave Function, Configurations, Isospin

Subject Areas: Quantum Mechanics, Theoretical Physics

1. Introduction

Error correction is regarded as a very important assignment of any human activity. Therefore, organizations dedicate efforts aiming to detect erroneous elements that may exist in the domain which is under its control. This is certainly a self-evident statement and specific aspects of this matter have acquired their own terminology. For example, QA (Quality Assurance) is used in industry; debugging is used in computer programming; devil’s advocate is used in theoretical debates. The present work describes two errors in theoretical physics which have not yet been corrected. Thus, it aims to make a contribution to this kind of activity among members of the physical community. Evidently, such an activity can only improve the understanding of different angles of the debated issue. The results which are derived below have a fundamental relevance to the present structure of theoretical physics. The basic nature of most of the arguments which are described in this paper means that all members of the physical community are expected to belong to its readership.

The paper discusses two topics: the form of atomic wave functions and interrelations between isospin states. These subjects are included in the physics curriculum as well as in relevant textbooks. The paper proves that corrections should be introduced to their presentation and that these corrections have far reaching consequences pertaining to the structure of theoretical physics.

The paper uses standard notation and units where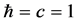. The second section proves that, unlike a common belief, the wave function of an atom having more than one electron has a multiconfiguration structure and that the central field approximation does not provide an adequate description of reality. This issue yields a straightforward solution to the dilemma called “the proton spin crisis”. The third section points out conse- quences of the usefulness of the isospin formalism for hadronic structure and explains why ordinary Dirac quarks provide a consistent description of the 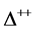baryon, etc. Concluding remarks are presented in the last section.

2. The Multiconfiguration Structure of Atomic States

Atomic states have played a key role in the construction of quantum mechanics. The importance of this issue is explained in this section where atoms of more than one electron are considered. It means that, together with the atomic nucleus, we have a problem of more than two bodies. For the simplicity of the discussion let us examine the ground state of the helium atom whose spin-parity state is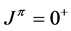. (Here 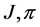denote the state’s total spin and its parity, respectively.)

A configuration of N electrons is an expression where each electron has a specific radial function n and an angular momentum l

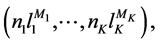(1)

where denotes the number of electrons having the same 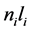values and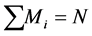. (In most cases the commas and the brackets are omitted from the expression.) Alternatively, a configuration is an expression where the total spin and parity of each electron are determined

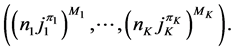(2)

The form (1) is used for the Schroedinger equation whereas the form (2) is used in a relativistic treatment where the Dirac equation holds. The form (2) is generally used below because of its broader validity. In physically interesting cases states of identical spin-1/2 particles are examined and an acceptable state abides by the Pauli exclusion principle.

It is well known that interactions conserves angular momentum. Furthermore, in the case of parity conserving interactions, like strong and electromagnetic interactions, each state has a well defined parity. Thus, our goal is to find the form of a quantum state where 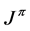take specific values. The configuration scheme is the route for reaching this goal. Indeed, this scheme is used in a construction of the entire Hilbert space where the required wave function is embedded. Therefore, “wave functions of any desired accuracy in principle can be obtained by the superposition of a sufficiently large number of configurations” [1] .

It should be pointed out that in the general case a configuration does not describe a unique 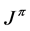state. The following simple example shows this issue. Let us examine the two electron configuration

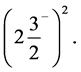(3)

This configuration can be used for a state where 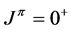and for a different state where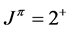. Each of these states is antisymmetric and abides by the Pauli exclusion principle. Therefore, the configuration (3) does not uniquely define the electronic state of a two-electron atom. It means that a configuration generally cannot be used as a complete description of an atomic state.

Let us now turn to the primary problems of this section.

Problem #1: Can an atomic quantum state be correctly described by a single configuration?

The following lines explain why the answer is negative. Let us take the ground state of the helium atom and examine the configurations

(4)

and (3). Evidently, laws of angular momentum addition prove that each of these configurations can yield an antisymmetric state (see e.g. [1] ). Therefore, the Hamiltonian submatrix of these states takes the form of the following Hermitian matrix (see [2] , p. 148)

(5)

The relevant diagonal form of this matrix can be obtained from an application of a standard procedure of matrix algebra. The results prove that the lowest eigenvalue is smaller than a and c and that the associated eigenfunction of the He atom ground state is a linear combination of the functions described by the con- figurations (3) and (4). This is certainly not the final word because this analysis can be extended to the case of a larger number of configurations where each of which can yield a state. A general discussion of the multifunction structure of a Hamiltonian eigenfunction can be found in Schiff' textbook (see [3] , pp. 128, 129). A discussion of the multiconfiguration structure of the Hamiltonian’s eigenfunctions of atomic states can be found in the quite early quantum mechanical literature [1] [2] . This discussion proves the following.

Answer #1: Excluding hydrogen-like atoms, atomic eigenfunctions of the Hamiltonian have a multicon- figuration structure.

Now, another problem arises:

Problem #2: Is there a dominant configuration in the description of the Helium atom ground state?

The answer to this problem is found in results of numerical calculations. These calculations have already been carried out in the early days of the computer era [4] . It turns out that

Answer #2: There is no dominant configuration in the structure of the ground state wave function of the He atom.

This outcome certainly has a more conspicuous effect in cases of other atomic states that have more than 2 electrons and/or states where, simply because in these cases there are more different configurations whose electronic state can be coupled to the required.

Unfortunately, these answers are apparently ignored by the general community. For example, due to its own rules, Wikipedia describes the present consensus. Contrary to the results derived above, the Wikipedia item examines electronic state of atoms and (as of March 2016) it uses a single configuration for describing the electronic ground state of each atom. The same discrepancy can be found in quantum mechanical textbooks (see [3] , p. 279, [5] , section 65, [6] , pp. 1418, 1419, etc.). It turns out that the single configuration form of atomic wave function stems from an assumption called The Central Field Approximation whose usefulness is apparently taken for granted. However, it is explained above that the single configuration description of an atomic state is very far away from reality.

The results found above have very significant implications. In particular, everything which is said above on electrons apply also to quarks. Therefore, the state of the proton’s quarks must be described by many configurations, and in most of them quarks have a higher angular momentum. It follows that spatial angular momentum makes a dominant contribution to the total proton spin and the instantaneous direction of the spin of each quark may be either up or down. This statistical effect means that quark’s spin makes a small contribution to the total spin of the proton. The validity of this conclusion has already been confirmed experimentally [7] .

Unfortunately, the general community assumes that the protons state is described by a single configuration of three quarks, where the two u quarks are described by the state and the d quark is in the 1s state. This is the reason for the dilemma called the “proton spin crisis” [8] [9] . The current version of Wikipedia states that this matter is still regarded as an unsettled physical problem.

It can be concluded that in the case of more than two particles the system takes a multiconfiguration structure, and that the Central Field Approximation does not yield a good description of the state.

3. The Wave Function of Members of the Same Isospin Multiplet

Heisenberg suggested the isospin symmetry in the early days of nuclear physics (see [10] , p. 106). This symmetry is based on the proton-neutron similarity with respect to strong interactions. Hence, since strong interactions are much stronger than electromagnetic interactions and the mass of the proton and the neutron takes very close values, the isospin formalism provides a good approximation for describing nuclear states. Mathematically, isospin is an SU(2) group, like that of spin. This formalism enables arranging nuclear states in irreducible sets called isospin multiplets. The usefulness of this approach is confirmed in experiment (see e.g. [11] , pp. 30, 74). An impressive similarity of isospin states is shown on p. 74 of [11] .

The same formalism has later been found useful for describing hadronic states where the quarks play the role of the proton and the neutron, respectively. In nuclear physics, isospin is denoted by the letter T and in particle physics it is denoted by the letter I. Hereafter, the letters denote total and single particle isospin, respectively.

As is well known, isospin raising and lowering operators have very useful applications. These operators, denoted respectively by and have the following property

(6)

Here denote total isospin and its third component, respectively (see [11] , p. 29). It follows that the successive application of covers all members of any irreducible representation of the SU(2) group. Moreover, an application of does not change the total isospin “or any other parts of the wave function” (see [11] , p. 29). From this discussion it follows that nuclear states on one hand and hadronic states on the other hand can be organized in irreducible multiplets where all members of each multiplet have the same isospin T. The following result stems from what is said above.

・ All members of a given isospin multiplet have the same spin and parity and also a very similar mass and a very similar structure of their wave function.

Hereafter, these important features are called the main isospin properties. The mass and structural differences between members of the same isospin multiplet are ascribed to the electromagnetic interactions and to the proton-neutron (or) mass difference. Like in many other discussions of states or processes where strong interactions are dominant, these small differences are ignored below.

The following example demonstrates the significance of the main isospin properties. Consider the decay of the ¹⁴O nucleus. This nucleus has a ground state and its daughter nucleus ¹⁴N has a ground state and a 2.31 MeV excited state (see Figure 1). Here the horizontal segments denote energy levels and of each state are written at the right hand side of the corresponding segment. The two arrows denote two decay channels of the ¹⁴O nucleus. More details of these nuclei are depicted in figure 7 of [12] .

It turns out that in spite of the much smaller phase space, more than 99% of the ¹⁴O decay events go to the 2.31 MeV excited state of the ¹⁴N. (The rest go to the ground state and to another excited state which is not shown in Figure 1.)

The main isospin properties explain this remarkable effect. The ground state of the ¹⁴N nucleus is an isospin singlet. On the other hand, the following energy levels belong to an isospin triplet: the ground state of ¹⁴C, the excited state of ¹⁴N and the ground state of ¹⁴O. Therefore, the main isospin properties show that the space-spin part of their wave function is (practically) the same. Hence, the nuclear matrix element of the transition to the excited state of the ¹⁴N nucleus is much larger than that of the transition to the ground state of this nucleus. It can be concluded that the ¹⁴O decay demonstrates the usefulness of the isospin symmetry in general and of one of its main features in particular: the space-spin components of the wave function of all members of an isospin multiplet are (practically) the same.

Let us examine another example which shows the usefulness of the isospin concept. This concept helps us understand the relationship between the multiplet of the two nucleons and that of the four baryons (see Figure 2). Here the three valence quarks of each baryon are written above its horizontal segment and its symbol is written below this segment. The numbers on the right hand side of the figure represent the average mass of the

corresponding multiplet (in MeV). For the nucleons and, whereas for the baryons and. Evidently, the baryons are heavier than the nucleons.

The data depicted in Figure 2 prove that the neutron and the baryon consist of the same valence quarks and that this property also holds for the proton and the baryon. Therefore, the baryon is an excited state of the neutron and the baryon is an excited state of the proton. (The relationship between the neutron and the and between the proton and the are analogous to the relationship between the two energy states of the ¹⁴N nucleus of Figure 1.) Applying well known rules of quantum mechanics, one finds that the wave function of the baryons must have single particle radial and/or angular excitation. Therefore, the main isospin properties prove that the and baryons’ wave function also takes the form of an excited state and their wave function has single particle radial and/or angular excitation. The multiconfiguration structure of a quantum system of more than two particles, which is discussed in the previous section, means that the state of every baryon consists of many configurations of this kind.

As shown in Figure 2, the and the baryons consist of three identical valence quarks. It turns out that mainstream textbooks argue that if one regards the spin-1/2 quarks as ordinary Dirac particles then the baryon is a symmetric s-wave ground state of its three uuu quarks (see e.g. [10] , p. 150; [13] , pp. 4, 5). The textbooks continue and argue that this is inconsistent with the Fermi-Dirac statistics. However, the symmetric s-wave ground state assumption of the baryon is inconsistent with the main isospin properties and the single configuration interpretation is inconsistent with the results of the second section. Hence, an interpretation of quarks as ordinary Dirac particles is compatible with the data of the and the baryons.

The main isospin properties and its foregoing outcome are ignored in quite a few textbooks. This matter has very far reaching consequences. For example, in order to prove the need for the QCD quark’s color degree of freedom, it is explained (see e.g. [13] ) that the (misinterpreted) “fiasco” of the state is the primary reason for the QCD construction [14] . An analogous argument has been put forward by H. Fritzsch, who is one of the QCD pioneers [14] . He argues that if quarks are regarded as ordinary Dirac particles then the three sss quarks of the baryon should be in a single particle ground state s-wave and that the result is inconsistent with the required Fermi-Dirac statistics of fermions. He says that this problem was the specific reason for the QCD construction [15] . However, this argument does not hold because the baryon is a member of a decuplet representation of the SU(3) group which also includes the four baryons (see [10] , pp. 146-150). Hence, the results obtained above for the baryon also hold for the baryon.

It is well known that QCD is the Standard Model sector of strong interactions. The discussion of this section shows that this theory has been constructed on the basis of an erroneous assumption which violates the outcome of the main isospin properties.

4. Concluding Remarks

This work discusses two topics and proves that the relevant parts of presently accepted theories contain errors. The analysis relies on well documented physical properties which are shown in the reference.

The first issue is the quantum state of atoms that have more than one electron and the quark state of baryons. The second section arrives at the following conclusions.

・ It is proved that the wave function of atoms having more than one electron has a multiconfiguration structure.

・ An analogous structure is found for the proton’s quarks.

・ The multiconfiguration structure provides a straightforward explanation for the dilemma called the proton spin crisis.

・ The assumption called central field approximation does not provide a good description of the actual quantum state.

The second issue is isospin which is known since the early days of nuclear physics. The third section discusses isospin and arrives at the following conclusions.

・ Nuclear states and hadronic states can be organized in sets called isospin multiplets.

・ All members of a given isospin multiplet have the same spin and parity and also a very similar mass and a very similar structure of their wave function.

・ The data support the usefulness of isospin as a good description of quantum states.

・ In particular, the state of the baryon can be explained by quarks which are ordinary Dirac particles and there is no need for the additional QCD color degree of freedom.

Error correction is an important task of every human community. This work points out two errors of presently accepted physical theories. In so doing it aims to launch a debate about the veracity of the results obtained above. Such a debate can certainly improve the understanding of several topics of theoretical physics.

Cite this paper

Eliahu Comay, (2016) Elementary Errors in Contemporary Theoretical Physics. Open Access Library Journal,03,1-6. doi: 10.4236/oalib.1102585

References