Open Access Library Journal
Vol.03 No.04(2016), Article ID:69181,8 pages
10.4236/oalib.1102583
Symmetric Hybrid Linear Multistep Method for General Third Order Differential Equations
Friday Oghenerukevwe Obarhua*, Sunday Jacob Kayode
Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria

Copyright © 2016 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 31 March 2016; accepted 14 April 2016; published 18 April 2016

ABSTRACT
A symmetric hybrid linear multistep method for direct solution of general third order ordinary differential equations is considered in this paper. The method is developed by interpolation and collocation approach using a combination of power series and exponential function as basis function. The consistency, stability, order and error constant of the method were determined. The results showed that the method is consistent, zero stable and of order five with low error constant. The accuracy compared favorably over existing methods with higher order of accuracy.
Keywords:
Symmetric, Hybrid Method, Exponential Function, Interpolation, Collocation
Subject Areas: Ordinary Differential Equation

1. Introduction
We consider the direct numerical solution of the general third order initial value problem of the form
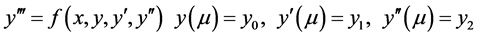 (1)
(1)
where 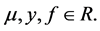
It is worth noting that this problem (1) can be modeled from the physical problems such as the thin film flow of a liquid in fluid dynamics, electromagnetic waves and gravity driven flow. Therefore, this type of problem is conventionally solved by reducing it to system of first order ordinary differential equations. [1] and some other authors pointed out that this type of problem can be solved directly to circumvent the inherent setbacks posed by the conventional method, [2] - [7] . These scholars proposed different methods of various degrees of accuracies using no other approximate basis functions other than power series.
[8] - [10] independently showed that the direct solution of the general second order initial value problems can be implemented without the need for predictors or starting values from other methods. In their work, they used power series as approximate solution to derive three-step LMM implemented in block modes. [11] investigated and developed a two-point block method in the form of Adams-Moulton type for solving general second order odes directly using variable step size while [5] and [12] proposed a linear multistep method for the direct solution of initial value problems of ordinary differential equations for special third order initial value problem and a hybrid multistep method to solve third order IVPs of ODEs respectively with constant step size. However, [11] developed a two-point four-step block method with variable step-size. In his work, the method was implemented at two points simultaneously in a block using four backward steps. Moreover, these constant and variable step sizes add little or nothing to the accuracy of the results due to the restriction of interpolation points to the order of the problems.
Recently, [13] and [14] figured out that in search for a method that gives better stability condition, the use of approximate solution which combines power series with exponential function is imperative. Therefore, in this work combination of power series and exponential function was used as basic function in determining a symmetric hybrid linear multistep method for the solution of problem (1) directly.
2. Materials and Methods
In this work, we considered using a combination of power series and exponential function in the form
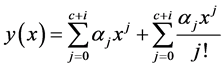 (2)
(2)
as the basic function for the development of the method, where c and i represent the number of collocation and interpolation points respectively.
The differential system of (2) is given as
 (3)
(3)
The basis function (2) is interpolated at all selected points 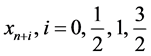 and the differential system (3) is collocated at only the grid points,
and the differential system (3) is collocated at only the grid points, 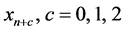 which gave rise to a system of equation of the form
which gave rise to a system of equation of the form
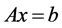 (4)
(4)
where
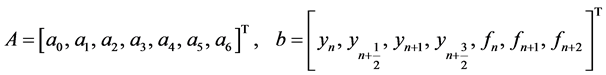 and
and

Solving (4) for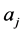 ’s,
’s, 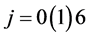 , using Gaussian elimination method and substituting it back into (2) gives a continuous hybrid method of the form
, using Gaussian elimination method and substituting it back into (2) gives a continuous hybrid method of the form
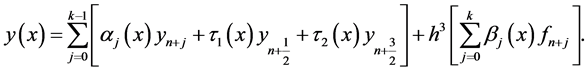 (5)
(5)
Using the transformation, 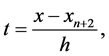 the continuous coefficients
the continuous coefficients 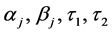 and their first and second derivatives are obtained as,
and their first and second derivatives are obtained as,
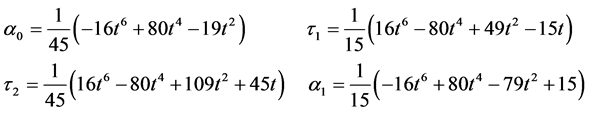



Evaluating Equations (6), (7) and (8) at the last end grid point where 



The order p and error constants of Equations (9), (10) and (11) are



3. Implementation of the Method
The starting values of the discrete method (9) obtained from (5) for third order problem of ordinary differential equations are generated in predictor-corrector mode of the same order of accuracy. The predictor methods and its derivatives of the same order with the corrector method are obtained using the same outlines discussed above to give



The order p and error constants of equations (12), (13) and (14) are



Other explicit schemes were developed to evaluate other starting values. Taylor series expansion is adopted for




and

4. Analysis of the Method
4.1. Order and Error Constant of the Method
In this paper we adopt the method proposed in [16] , with the linear operator

and the linear operator L is defined as:

where 



Therefore, we say that the method has order p if,
In this paper, it reveals that the methods (9), (10) and (11) have order



4.2. Zero Stability
A linear multistep method (LMM) is said to be zero-stable, if no root of the first characteristic polynomial 


For our method
Hence our method is zero stable.
4.3. Region of Absolute Stability of the Method
Let us consider the stability polynomial of the linear multistep method defined by 




The boundary locus curve is obtained by substituting 


4.4. Convergence of the Method
For a linear multistep method (LMM) to be convergent, the necessary and sufficient conditions are that the method must be consistent and zero-stable, therefore from the analysis, our method is convergent.
5. Numerical Experiments
To test the effectiveness and the accuracy of the new method, the method is used to solve three test problems below and the results are shown in Tables 1-3.
Problem 1.
Theoretical solution:
Problem 2.
Theoretical solution:
Problem 3.
Theoretical solution:
Problem 4.
Theoretical solution:
6. Discussion of Result
A new two-step symmetric hybrid method of order 5 is proposed for the direct solution of third order differential equations. The maim method and the predictors of same order were derived from the same procedure of collocation and interpolation method. The methods are then applied to on some existing problems and the results were displayed on the Tables 1-4. The errors were compared with those of [5] [7] [12] [15] [17] [18] . It was observed from the tables that the new method displayed better accuracy over the existing methods.
Table 1. In this example, the numerical solution of our methods of order 5 was compared with the method of [15] and [7] , both are of order 7. This is shown in Table 1 below.
Table 2. The absolute errors of predictor-corrector method of order five is compared with those of Block methods [12] and [5] .
Table 3. The absolute errors of predictor-corrector method of order five is compared with that of Block method, [16] and [7] both are of order seven.
Table 4. The absolute errors of predictor-corrector method of order five is compared with that of [17] , where they developed modified Runge-Kutta methods and [18] both are of order seven.
7. Conclusion
The combination of power series and exponential function collocation method was used to produce a two-step continuous-hybrid method. The method obtained was used to solve some mildly-stiff third order ordinary differential equations. The new method compared favorably in terms of accuracy with the existing methods of higher order and step number. Our future research will be focused on more introductions of grid and off-grid points to enhance global error estimations.
Cite this paper
Friday Oghenerukevwe Obarhua,Sunday Jacob Kayode, (2016) Symmetric Hybrid Linear Multistep Method for General Third Order Differential Equations. Open Access Library Journal,03,1-8. doi: 10.4236/oalib.1102583
References
- 1. Kayode, S.J. (2009) A Zero Stable Method for Direct Solution of Fourth Order Ordinary Differential Equations. American Journal of Applied Sciences, 5, 1461-1466.
- 2. Kayode, S.J. and Adeyeye, O. (2013) Two-Step Two-Point Hybrid Methods for General Second Order Differential Equations. African Journal of Mathematics and Computer Science Research, 6, 191-196.
- 3. Majid, Z.A., Azmi, N.A. and Suleiman, M.B. (2009) Solving Second Order Ordinary Differential Equations Using Two Point Four Step Direct Implicit Block Method. European Journal of Scientific Research, 31, 29-36.
- 4. Kayode, S.J. and Obarhua, F.O. (2015) 3-Step y-Function Hybrid Methods for Direct Numerical Integration of Second Order IVPs in ODEs. Theoretical Mathematics & Applications, 5, 39-51.
- 5. Mohammed, U. and Adeniyi, R.B. (2014) A Three Step Implicit Hybrid Linear Multistep Method for the Solution of Third Order Ordinary Differential Equations. General Mathematics Notes, 25, 62-74.
- 6. Kayode, S.J. and Obarhua, F.O. (2013) Continuous y-Function Hybrid Methods for Direct Solution of Differential Equations. International Journal of Differential Equations and Applications, 6, 191-196.
- 7. Awoyemi, D.O., Kayode, S.J. and Adoghe, L.O. (2014) A Four-Point Fully Implicit Method for Numerical Integration of Third-Order Ordinary Differential Equations. International Journal of Physical Sciences, 9, 7-12.
http://dx.doi.org/10.5897/IJPS2013.4019 - 8. Jator, S.N. (2007) A Sixth Order Linear Multistep Method for Direct Solution of . International Journal of Pure and Applied Mathematics, 40, 457-472.
- 9. Mohammed, U. (2010) A Class of Implicit Five Step Block Method for General Second Order Ordinary Differential Equations. Journal of Nigerian Mathematical Society, 30, 375-388.
- 10. Jator, S.N. and Li, J. (2009) A Self Starting Linear Multistep Method for the General Second Order Initial Value Problems. International Journal of Computer Mathematics, 86, 817-836.
http://dx.doi.org/10.1080/00207160701708250 - 11. Majid, Z.A., Azmi, N.A., Suleiman, M. and Ibrahim, Z.B. (2012) Solving Directly General Third Order Ordinary Differential Equations Using Two-Point Four-Step Block Method. Sians Malaysiana, 41, 623-632.
- 12. Olabode, B.T. and Yusuf, Y. (2009) A New Block Method for Special Third Order Ordinary Differential Equations. Journal of Mathematics and Statistics, 5, 167-170.
http://dx.doi.org/10.3844/jmssp.2009.167.170 - 13. Sunday, J., Odekunle, M.R., James, A.A. and Adesanya, A.O. (2014) Numerical Solution of Stiff and Oscillatory Differential Equations Using a Block Integrator. British Journal of Mathematics & Computer Science, 4, 2471-2481.
http://dx.doi.org/10.9734/BJMCS/2014/8563 - 14. Momoh, A.A., Adesanya, A.O., Fasasi, K.M. and Tahir, A. (2014) A New Numerical Integrator for the Solution of Stiff First Order Ordinary Differential Equations. Engineering and Mathematics Letters, 4, 1-10.
- 15. Olabode, B.T. (2007) Some Linear Multistep Methods for Special and General Third Order Initial Value Problems in Ordinary Differential Equations. PhD Thesis, Federal University of Technology, Akure. (Unpublished)
- 16. Lambert, J.D. (1973) Computational Methods in Ordinary Differential Equations. John Wiley & Sons Inc., New-York.
- 17. Agam, S.A. and Irhebbhude, M.E. (2011) A Modification of the Fourth Order Runge-Kutta Method for Third Order Ordinary Differential Equations ODEs. ABACUS, Journal of the Mathematical Association of Nigeria, 38, 87-95.
- 18. Yahaya, Y.A. and Badmus, A.M. (2007) A 3-Step Hybrid Collocation Method for Special Third Order Initial Value Problems of ODEs. International Journal of Numerical Mathematics, 3, 306-314.
NOTES
*Corresponding author.















