Int. J. Communications, Network and System Sciences, 2011, 4, 487-494
doi:10.4236/ijcns.2011.48060 Published Online August 2011 (http://www.SciRP.org/journal/ijcns)
Fairness Aware Group Proportional Frequency Domain
Resource Allocation in L-SC-FDMA Based Uplink*
Irfan Ahmed1, Amr Mohamed2
1College of Computers and Information Technology, Taif University, Taif, KSA
2College of Computer Science and Engineering, Qatar University, Doha, Qatar
Received May 31, 2011; revised July 2, 2011; accepted July 11, 2011
Abstract
This paper presents virtual clusters based proportional fairness and resource allocation scheme for Localized
Single Carrier Frequency Division Multiple Access (L-SC-FDMA). L-SC-FDMA has been selected as the
uplink transmission scheme in 3GPP Long Term Evolution (LTE) due to its low Peak to Average Power Ra-
tio (PAPR) over OFDMA in general and high rate-sum capacity over Interleaved SC-FDMA in particular.
Virtual cluster-based proportional fairness (VCPF) scheduler exploits the link adaptation information avail-
able at MAC layer to form virtual clusters. The distributed proportional fairness scheduler ensures a mini-
mum throughput for all users in the coverage area by assigning contiguous RBs, proportional to the
throughput and the number of users in a particular cluster or group. Simulations have been performed using
practical scenario of uniformly distributed users in Rayleigh faded coverage area and design formulas have
been devised for network planning to get the best possible fairness with promising level of quality of service
(QoS).
Keywords: Radio Resource Allocation, Fairness, LTE
1. Introduction
Nowadays, growing demands of broadband services are
provoking the deployment of 4G technologies like long
term evolution (LTE) and LTE-Advanced [1]. LTE has
paved the way for the prevalent adoption of orthogonal
frequency division multiple access (OFDMA) as the key
technology for providing high spectrum efficiency and
protection against multip ath fad ing . LTE-Advan ced tech-
nology is expected to provide peak data rates in the order
of 1 Gbps in downlink and 500 Mbps in uplink with a 20
MHz spectrum allocation [2]. OFDM has been selected
as transmission technology of most of the other wireless
broadband standards. In multiuser application, OFDM
can be used as OFDM-TDMA (time division multiplex-
ing access), OFDM-CDMA (code division multiplexing
access) or OFDM-FDMA (frequency division multi-
plexing access). In case of OFDM-TDMA or OFDM-
CDMA each user has to transmit its signal over the entire
spectrum that leads to an averaged-down effect in the
presence of deep fading and narrowband interference,
whereas, in OFDM-FDMA, commonly called OFDMA
(orthogonal frequency division multiplexing access) total
bandwidth is divided into frequency blocks (one or group
of subcarriers).
An OFDMA system is defined as one in which each
user occupies a subset of frequency blocks and each
block is assigned exclusively to one user at any time,
thus the radio resource are allocated in both the fre-
quency (subcarrier) and time domains.
However, despite of numerous advantages of OFDM
and OFDMA, their major disadvantage is that their wave-
forms have high peak to average power ratio (PAPR).
High PAPR is problematic for uplink transmission where
the mobile transmission power is usually limited. For
PAPR reduction, 3GPP-LTE agreed on using single car-
rier frequency division multiple access (SCFDMA) trans-
mission with cyclic prefix in the uplink. Therefore, In
LTE system, OFDMA has been selected as the downlink
access scheme and single carrier frequency division mul-
tiple access (SC-FDMA) has been chosen as the uplink
access scheme [3].
This paper investigates proportional groups based
channel dependent resource allocation scheme that pro-
*This work is supported by the Qatar Telecom (Qtel) Grant No.
Q
UEX-
Q
tel-09/10-10.

I. AHMED ET AL. 488
vides a minimum required throughput with fairness
among active users in SC-FDMA LTE uplink, regardless
of their distance from the enhanced NodeB (eNB) or the
base station. Since SC-FDMA is based on OFDMA with
an additional Discrete Fourier Transform (DFT) block in
the transmitter and Inverse DFT (IDFT) block in the re-
ceiver, the same benefits in terms of multipath mitigation
and channel equalization are achievable in addition to
low peak-to-average power ratio (PAPR). This property
is very important in uplink as the user equipment (UE) is
generally a handheld device with limited transmit power
capacity.
SC-FDMA has two types of subcarrier mapping: lo-
calized SC-FDMA (L-SC-FDMA) and interleaved SC-
FDMA (I-SC-FDMA). In L-SC-FDMA subcarriers are
mapped in contiguous fashion to obtain the frequency
selective diversity whereas in I-SC-FDMA, users are
assigned distributed subcarriers over the entire band-
width which provides multi-user diversity. L-SC-FDMA
has been chosen for LTE uplink due to high rate-sum
capacity [4] and 2.7 dB (16QAM, 10% bandwidth usage)
lower PAPR [5] as compared to I-SC-FDMA. In litera-
ture, the following three types of subcarrier/resource
blocks allocation schemes are widely discussed [6]: 1)
throughput optimization; 2) proportional fairness; and 3)
max-min fairness. Throughput optimization implies that
the greater the throughput of subcarrier j for user i, the
greater the tendency we perform the corresponding sub-
carrier allocation, proportional fairness schemes states
that in order to achieve the proportio nal fairness the util-
ity function should be , and max-min
tends to allocate a subcarrier to a user who has minimum
throughput in order to minimize the gap between the
minimum and maximum achieved throughput for any
user in the cell.
 
ln
ii i
Uf f
Considerable research work has already been done in
scheduling and radio resource allocation for LTE down-
link. However, the optimality solutions and scheduling
algorithms derived for downlink case, cannot be directly
applied to the uplink due to differences in terms of
transmission technology (L-SC-FDMA) and network
resource constraints (contiguous physical resource blocks
(PRB)). For SC-FDMA, a channel scheduling algorithm
regardless of the contiguity in frequency resource alloca-
tion has been presented in [4]. F. D. Calabrese et al. [7]
proposed a search-tree based channel aware packet sche-
duling algorithm in which resources are equally shared
among users.
Proportional fair scheduling for high throughput 3G/
4G networks has been investigated in [8,9]. The joint
scheduling of OFDM subcarriers with power allocation
for uplink of a single cell has been discussed in [9]. The
problem has been formulated as a constrained non-linear
optimization, then integer subcarrier assignment has been
obtained through sub-optimal heuristic to break the ties
of allocating partial subcarriers to multiple users. Util-
ity-based proportional fair scheduling for uplink single
cell system has been investigated in [8]. A Game theo-
retical formulation of optimizing the allocation of OF-
DMA subcarriers and TDMA resource blocks for LTE
networks has been presented, which leads to the design
of an algorithm that achieves proportional fairness while
providing throughput maximization, but this paper does
not cater the contingency of subcarriers.
None of the previous work mentioned above consid-
ered the real world scenario faced by cellular operators
where some users continuously starving from bandwidth
and some users (with favorable channel conditions and
proximity with eNB) enjoy high throughput. In a uni-
formly populated coverage area of eNB, the number of
distant UEs with low signal-to-noise ratio (SNR) in outer
circular ring are larger than the UEs with better SNR and
high throughput in inner ring (area closed to eNB).
Contribution
The main contributions and significance of our work are
two-fold:
1) Virtual group based proportional fairness using
MAC layer Modulation and Coding Scheme (MCS) in-
formation;
2) Frequency domain resource allocation based on vir-
tual groups.
This paper is organized as follows: In Section 2 we
describe the problem statement and the way we formu-
late the problem. In Section 3, a novel MCS based virtual
proportional group fairness for frequency domain re-
source allocation in L-SC-FDMA has been presented.
Performance evaluation and comparisons of proposed
scheme are provided in Section 4, followed by conclu-
sions in Sec t ion 5.
2. Problem Statement
We consider the problem of Frequency domain schedul-
Figure 1. System model.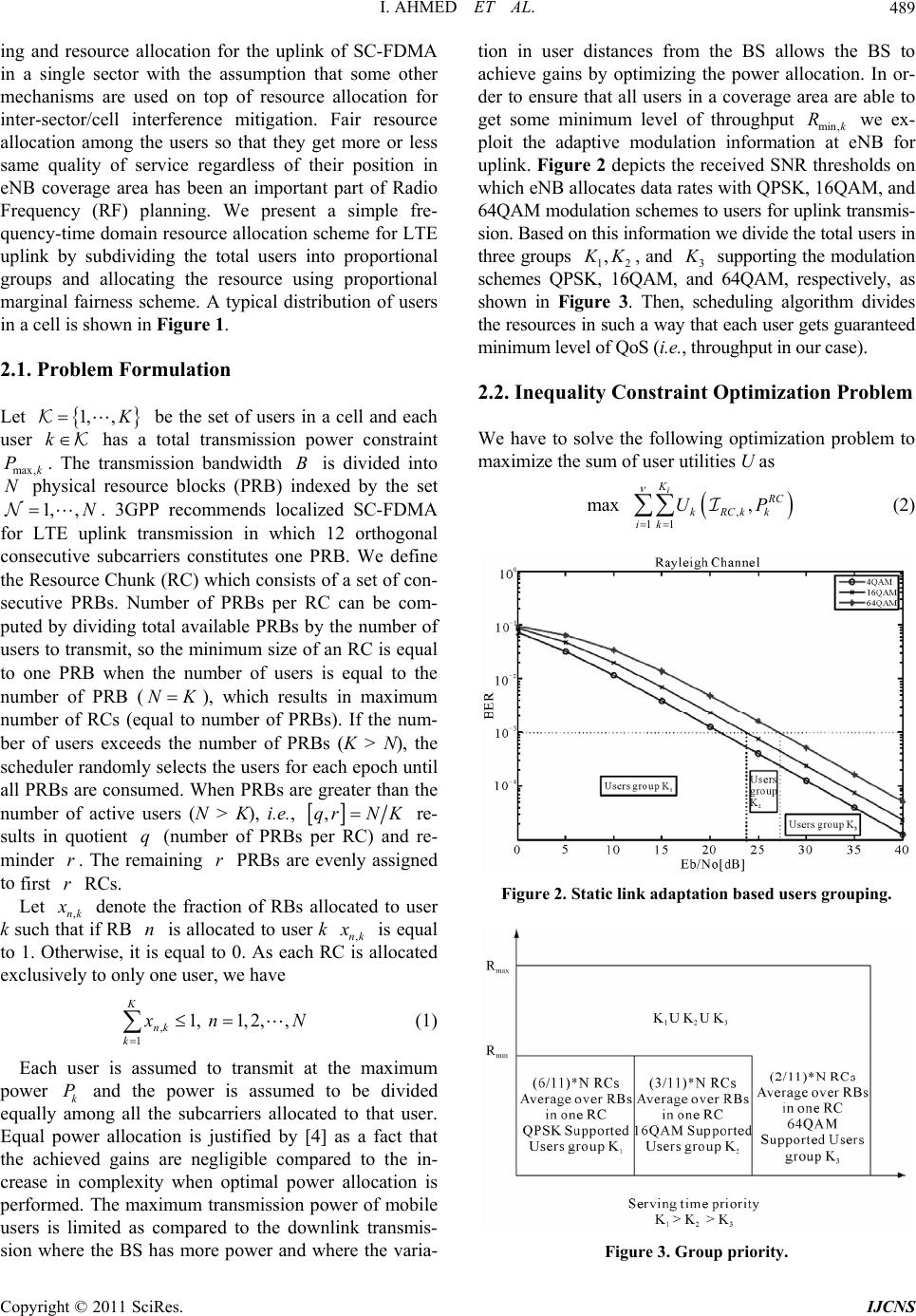

I. AHMED ET AL.489

ing and resource allocation for the uplink of SC-FDMA
in a single sector with the assumption that some other
mechanisms are used on top of resource allocation for
inter-sector/cell interference mitigation. Fair resource
allocation among the users so that they get more or less
same quality of service regardless of their position in
eNB coverage area has been an important part of Radio
Frequency (RF) planning. We present a simple fre-
quency-time domain resource allocation scheme for LTE
uplink by subdividing the total users into proportional
groups and allocating the resource using proportional
marginal fairness scheme. A typical distribution of users
in a cell is shown in Figure 1.
2.1. Problem Formulation
Let

1, ,
K

k
,k
1,, N
be the set of users in a cell and each
user has a total transmission power constraint
. The transmission bandwidth is divided into
physical resource blocks (PRB) indexed by the set
max
P
N
B

. 3GPP recommends localized SC-FDMA
for LTE uplink transmission in which 12 orthogonal
consecutive subcarriers constitutes one PRB. We define
the Resource Chunk (RC) which consists of a set of con-
secutive PRBs. Number of PRBs per RC can be com-
puted by dividing total available PRBs by the number of
users to transmit, so the minimum size of an RC is equal
to one PRB when the number of users is equal to the
number of PRB (), which results in maximum
number of RCs (equal to number of PRBs). If the num-
ber of users exceeds the number of PRBs (K > N), the
scheduler randomly selects the users for each epoch until
all PRBs are consumed. When PRBs are greater than the
number of active users (N > K), i.e.,
NK


,qrN K re-
sults in quotient (number of PRBs per RC) and re-
minder . The remaining PRBs are evenly assigned
to first RCs.
q
r
r
r
Let ,nk
x
denote the fraction of RBs allocated to user
k such that if RB is allocated to user k ,nk n
x
is equal
to 1. Otherwise, it is equal to 0. As each RC is allocated
exclusi vely to only one user , we have
,
1
1, 1,2,,
K
nk
k
x
n


N (1)
Each user is assumed to transmit at the maximum
power k and the power is assumed to be divided
equally among all the subcarriers allocated to that user.
Equal power allocation is justified by [4] as a fact that
the achieved gains are negligible compared to the in-
crease in complexity when optimal power allocation is
performed. The maximum transmission power of mobile
users is limited as compared to the downlink transmis-
sion where the BS has more power and where the varia-
tion in user distances from the BS allows the BS to
achieve gains by optimizing the power allocation. In or-
der to ensure that all users in a coverage area are able to
get some minimum level of throughput min,k we ex-
ploit the adaptive modulation information at eNB for
uplink. Figure 2 depicts the received SNR thresholds on
which eNB allocates data rates with QPSK, 16QAM, and
64QAM modulation schemes to users for uplink transmis-
sion. Based on this information we divide the total users in
three groups 12
P
R
,
K
K, and 3
K
supporting the modulation
schemes QPSK, 16QAM, and 64QAM, respectively, as
shown in Figure 3. Then, scheduling algorithm divides
the resources in such a way that each user gets guaranteed
minimum level of QoS (i.e., throughput in our case).
2.2. Inequality Constraint Optimization Problem
We have to solve the following optimization problem to
maximize the sum of user utilities U as

,
11 ,
i
K

max
R
C
kRCkk
ik
UP


  (2)
Figure 2. Static link adaptation based users grouping.
Figure 3. Group priority.

I. AHMED ET AL. 490
i
subject to
,max;1,, kk
PP kK (3)
,
1
1;1, ,i
K
nk K
k
x
n


N (4)
where

is the number of user groups, 1,,i


,
,
R
Ck is the number of radio resource blocks allocated
to the user , and

k
R
C
k
P is the average power allocated
by the user to assigned resource block. In general,
the utility function is a set of services that determine the
user satisfactions in terms of throughput, delay or other
QoS criteria. In our case, one example that considers
merely throughput maximization is to define the utility
function as the effective throughput that a user can
achieve with the given radio resource blocks and re-
ceived SNR
k
,nk

as follows:

,
RC,, 2
1
,log1
Nnk
RC
kk nk
n
B
RP x
N








 

(5)
where is called SNR gap [11]. It indicates the dif-
ference between the SNR needed to achieve a certain
transmission rate for practical M-QAM and the theoreti-
cal limit (Shannon capacity)


2ln 5BER
3


(6)
In SC-FDMA, the noise contribution of highly attenu-
ated subcarriers can be rather large, therefore Minimum
Mean Square Error (MMSE) equalizer is preferred over
Zero Forcing (ZF) equalizer [10]. The SNR at the output
of MMSE equalizer, when each user is assumed to trans-
mit at maximum power ,maxkk
and the power is to
be divided equally among all the RCs allocated to that
user, is given by [4]
PP

,
1
RC, ,
RC, ,
1
,
1
1
sub k
kk
ik
iI
kik
PN
N













1






(7)
where 2
,,ikk ikn
PH

 , and 2
n

is the noise power
density.
,ik
H
is the channel gain when subcarrier i is allocated
to user k, ,
s
ub k is the set of subcarriers assigned to user
. Practically, the channel gain depends upon various
factors, including thermal noise at receiver, receiver
noise figure, antenna gains, distance between transmitter
and receiver, path loss exponent, log normal shadowing
and fading, hence we can write
I
k
,10,
10log 10log
ikk ikik10,
H
pd F

  (8)
In above equation,  (83.46 dB) is a constant de-
pending upon thermal noise at receiver, receiver noise
figure, an d antenna gains, (3.5) is path loss exponent,
k is the distance in Km from UE to eNB, ,ik
p
dk

(10.5 dB) is shadowing parameter modeled by a nor-
mally distributed random variable with standard devia-
tion 8 dB, and ,ik
F
corresponds to Rayleigh fading.
3. Group Fairness Scheduling Algorithm
We divide the number of active users at each epoch (i.e.,
transmission time interval or TTI) into

number of
groups, which is equal to number of supported modula-
tion schemes in transmission technolog y as,


123
,,,,
K
KK KK

 (9)
The users in each group contend for RBs separately.
The maximum number of RBs that can be allocated to
1
K
group is given by



1
1
2
N 2m
1
g
i
ax 21
2m 1
log lo
lo i
K
K
ii
K
i
MM
K
N
ax
g
K
MM











(10)
where

 2max 22
j

max
loglog log
iKK
NMMM

ij
M




M
max is the largest constellation size supported by
M-ary signaling and 1
K
M
is the constellation size sup-
ported by users in group 1
K
. Similarly, 2
K
N, 3
K
N, and
so on.
Static link adaptation technique has been used to
group the users. In this method, the instantaneous SNR
of each user is compared with the theoretical BER-SNR
curves in fading channel as shown in Figure 3, and
based on the received SNR (modulation scheme) each
user has been allocated a specific group. For Rayleigh
fading channel the SNR corresponding to target BER
() for rectangular MQAM signaling can be com-
puted as [11, (6.61)]
ta
b
Prget
2
target
2
target
2
21
2
ˆ
11 ˆ
b
M
b
SNR
ˆ
M
M
P
P















 (11)
where


2
ˆ21log
M
M
MM   and


2
ˆM
 3log1MM .


R
d s N
by
In Figure 3 min is the minimum av erag e throug hput
that will be guaranteed withB
SC number of subcarri-
ers per RB aymbol number of OFDM symbols per
TTI, and is given
n
R
N
:

I. AHMED ET AL.491

RB
SC symbol
min, ,1,,
TTI msec
i
K
i
i
N NN
Ri
K


R
(12)
and

min min,
1, ,
inf i
i
R
 
 (13)
Since the optimization problem in (2) has a nonlinear
objective function with nonlinear and discrete constraints
that requires a complex combinatorial comparison, we
present a resource chunk allocation algorithm that maxi-
mizes the sum of user marginal utility function in user
group.
Marginal utility is defined as the difference between
the utility obtained when chunk is allocated to user k
and the utility of user kin the absence of a chunk allo-
cation at each epoch [8]
n






,RC,
ln ln
nkkk kk
URnNURnN 

RC,
(14)
3.1. Algorithm
This algorithm applies independently and identically on
each group.
Initialization:
Set of potential candidate users,

can,1 can,2can,
,,,
t
C
II I (15)
Set of
K
number of randomly selected users from
number of candidates, C

user,1 user,2user,
,,,
tt
K
II I


(16)
Set of resource chunks RCs,

RC,1 RC,2RC,
,,,
t
L
II I (17)
where = total number of RBs in B)/(Number of RBs
per user).
L
Objective: To assign an RC to user in order to
maximize the marginal utility for a given set of
nk
K
initialization
i = 1, 2, 3
K = No. of users
for K = 0 to K do
2
for K = 0 to K − K do
3 2
K = (K − K2) − K
1 3
calculate Rmin,i (Ki, NKi)
end for
end for
evaluate infi∈{1,2,3} Rmin,i
Algorithm 1. Rmin,i for every value of K1, K2 and K3 with
K = 10.
contended users, i.e.,
 
user, argmax t
nn
k
k
Ik


 (18)
Three steps (user-RC) assignment is given below: \\
Step I: Find the (user, RC) pair that gives highest mar-
ginal utility value
** ,
,
,argmax
tt
kn
kn
kn 




 (19)
Step II: Allocate RC to user
*
n* k
 





**
user, user,user,
ˆnnn t
kk k
IInnI k  (20)
Step III: Delete the allocated RC from the available
RC set
t

RC,
tt
n
I
 (21)
Repeat the steps I, II, and III, until all RCs are allo-
cated.
3.2. Complexity Analysis
The proposed algorithm first determines the number of
RCs and the number of RBs per RC for each group , then
within the group it performs a linear search on the users
and RCs in order to find th e user-RC pair th at maximizes
the utility function. For proposed algorithm the result of
[8, (12)] modifies to the following:
2
RC,
1
2
1
complexity
i
i
Ki
i
Ki
i
ii
NK
Nr
K
q




















(22)
where i and i are quotient and remainder from q r
i
K
i, respectively, and RC, i
NK
K
N is the number of
RCs allocated to i
K
group. From the elementary cal-
culus,



2
222
abc abc 

 (23)
therefore, our proposed algorithm provides a gain of at
least
33 12 21
1223 13
2KK
KK KK
NN NN NN
qq qq qq




.
(when 0
i
r

) over the algorithm presented in [8].
4. Performance Evaluation
In this section, we provide computer simulations using
MATLAB. Sum-throughput and indiv idual user through-
put have been compared with Round Robin (RR) and
logarithmic utility based proportional fairness (PF) algo-
rithm [12].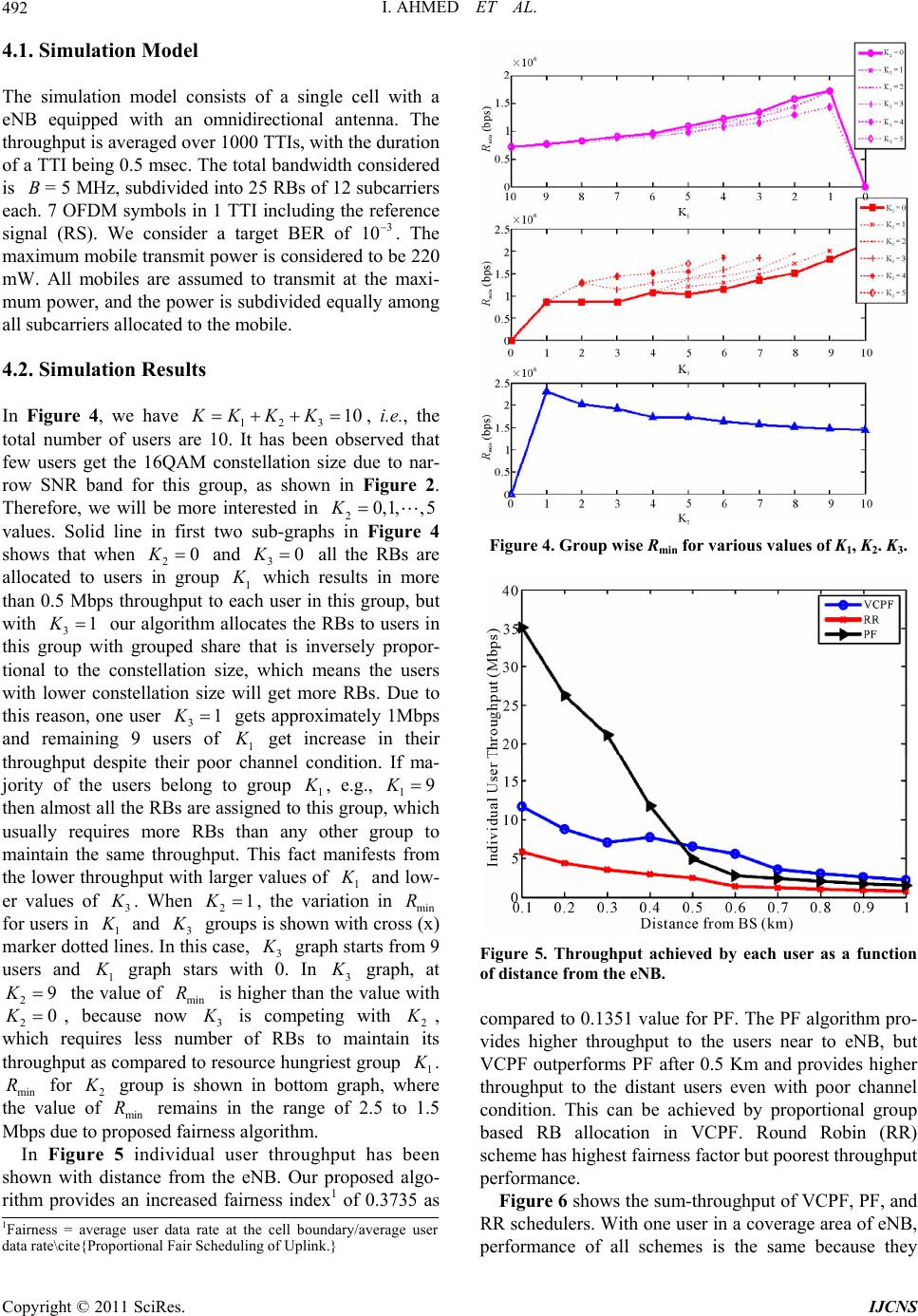

I. AHMED ET AL. 492
4.1. Simulation Model
The simulation model consists of a single cell with a
eNB equipped with an omnidirectional antenna. The
throughput is av erag ed over 1000 TTIs , with the dur ation
of a TTI being 0.5 msec. The total bandwidth considered
is = 5 MHz, subdivided into 25 RBs of 12 subcarriers
each. 7 OFDM symbols in 1 TTI including the reference
signal (RS). We consider a target BER of
B
3
10

. The
maximum mobile transmit power is considered to be 220
mW. All mobiles are assumed to transmit at the maxi-
mum power, and the power is subdivided equally among
all subcarriers allocated to the mobile.
4.2. Simulation Results
In Figure 4, we have 123 , i.e., the
total number of users are 10. It has been observed that
few users get the 16QAM constellation size due to nar-
row SNR band for this group, as shown in Figure 2.
Therefore, we will be more interested in 2
values. Solid line in first two sub-graphs in Figure 4
shows that when 2 and 3 all the RBs are
allocated to users in group 1
10KK KK
K
0 0K
0,1, ,5 
K
K
which results in more
than 0.5 Mbps throughput to each user in this group, but
with 3 our algorithm allocates the RBs to users in
this group with grouped share that is inversely propor-
tional to the constellation size, which means the users
with lower constellation size will get more RBs. Due to
this reason, one user 3 gets approximately 1Mbps
and remaining 9 users of 1
1K
1K
K
get increase in their
throughput despite their poor channel condition. If ma-
jority of the users belong to group 1
K
, e.g., 19K

then almost all the RBs are assigned to this group, which
usually requires more RBs than any other group to
maintain the same throughput. This fact manifests from
the lower throughput with larger values of 1
K
and low-
er values of 3
K
. When 21K

, the variation in min
for users in 1
R
K
and 3
K
groups is shown with cross (x)
marker dotted lines. In this case, 3
K
graph starts from 9
users and 1
K
graph stars with 0. In 3
K
graph, at
the value of mi is higher than the value with
2, because now 3
2
K
K9 0n
R
K
is competing with 2
K
,
which requires less number of RBs to maintain its
throughput as compared to resource hungr iest group 1
K
.
min for 2
R
K
group is shown in bottom graph, where
the value of min remains in the range of 2.5 to 1.5
Mbps due to proposed fairness algorithm.
R
In Figure 5 individual user throughput has been
shown with distance from the eNB. Our proposed algo-
rithm provides an increased fairness index1 of 0.3735 as
Figure 4. Group wise Rmin for various values of K1, K2. K3.
Figure 5. Throughput achieved by each user as a function
of distance from the eNB.
compared to 0.1351 value for PF. The PF algorithm pro-
vides higher throughput to the users near to eNB, but
VCPF outperforms PF after 0.5 Km and provides higher
throughput to the distant users even with poor channel
condition. This can be achieved by proportional group
based RB allocation in VCPF. Round Robin (RR)
scheme has highest fairness factor but poorest throughput
performance.
Figure 6 shows the sum-throu ghput of VCPF, PF, and
RR schedule rs. With one user in a cov erage are a of eNB,
performance of all schemes is the same because they
1Fairness = average user data rate at the cell
b
oundary/average user
data rate\cite{Proportional Fair Scheduling of Uplink.}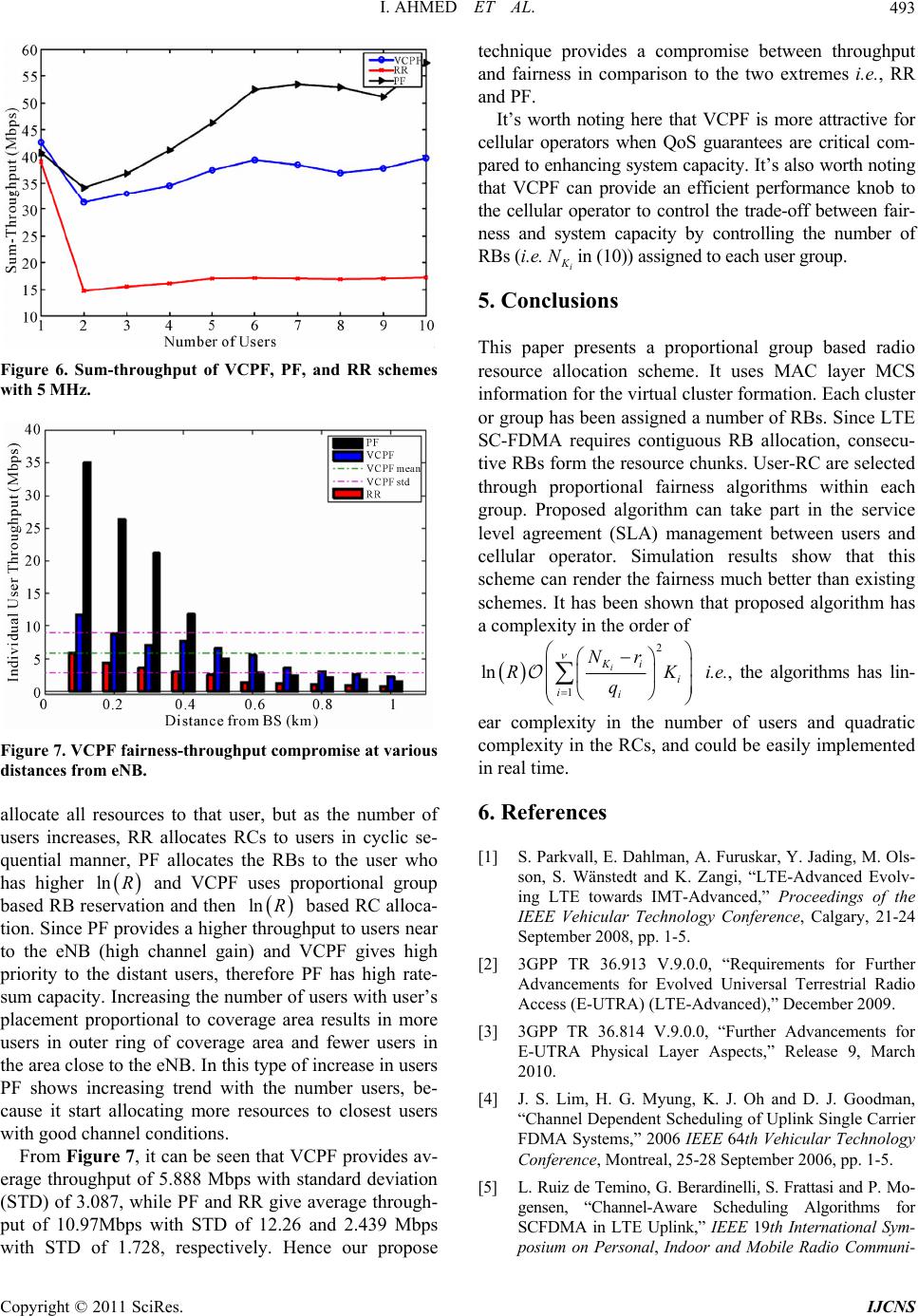

I. AHMED ET AL.493
Figure 6. Sum-throughput of VCPF, PF, and RR schemes
with 5 MHz.
Figure 7. VCPF fairness-thro ughput compromise at var ious
distances from eNB.
allocate all resources to that user, but as the number of
users increases, RR allocates RCs to users in cyclic se-
quential manner, PF allocates the RBs to the user who
has higher and VCPF uses proportional group
based RB reservation and then based RC alloca-
tion. Since PF provides a higher throughput to users near
to the eNB (high channel gain) and VCPF gives high
priority to the distant users, therefore PF has high rate-
sum capacity. Increasing the number of users with user’s
placement proportional to coverage area results in more
users in outer ring of coverage area and fewer users in
the area close to the eNB. In this type of increase in users
PF shows increasing trend with the number users, be-
cause it start allocating more resources to closest users
with good channel conditions.

ln R

ln R
From Figure 7, it can be seen that VCPF provides av-
erage throughput of 5.888 Mbps with standard deviation
(STD) of 3.087, while PF and RR give average through-
put of 10.97Mbps with STD of 12.26 and 2.439 Mbps
with STD of 1.728, respectively. Hence our propose
technique provides a compromise between throughput
and fairness in comparison to the two extremes i.e., RR
and PF.
It’s worth noting here that VCPF is more attractive for
cellular operators when QoS guarantees are critical com-
pared to enhancing system capacity. It’s also worth noting
that VCPF can provide an efficient performance knob to
the cellular operator to control the trade-off between fair-
ness and system capacity by controlling the number of
RBs (i.e. i
K
Nin (10)) assigned to each user group.
5. Conclusions
This paper presents a proportional group based radio
resource allocation scheme. It uses MAC layer MCS
information for the virtual cluster formation. Each cluster
or group has been assigned a number of RBs. Since LTE
SC-FDMA requires contiguous RB allocation, consecu-
tive RBs form the resource chunks. User-RC are selected
through proportional fairness algorithms within each
group. Proposed algorithm can take part in the service
level agreement (SLA) management between users and
cellular operator. Simulation results show that this
scheme can render the fairness much better than existing
schemes. It has been shown that proposed algorithm has
a complexity in the order of

2
1
ln i
Ki
i
ii
Nr
R
q











K


i.e., the algorithms has lin-
ear complexity in the number of users and quadratic
complexity in the RCs, and could be easily implemented
in real time.
6. References
[1] S. Parkvall, E. Dahlman, A. Furuskar, Y. Jading, M. Ols-
son, S. Wänstedt and K. Zangi, “LTE-Advanced Evolv-
ing LTE towards IMT-Advanced,” Proceedings of the
IEEE Vehicular Technology Conference, Calgary, 21-24
September 2008, pp. 1-5.
[2] 3GPP TR 36.913 V.9.0.0, “Requirements for Further
Advancements for Evolved Universal Terrestrial Radio
Access (E-UTRA) (LTE-Advanced),” December 2009.
[3] 3GPP TR 36.814 V.9.0.0, “Further Advancements for
E-UTRA Physical Layer Aspects,” Release 9, March
2010.
[4] J. S. Lim, H. G. Myung, K. J. Oh and D. J. Goodman,
“Channel Dependent Scheduling of Uplink Single Carrier
FDMA Systems,” 2006 IEEE 64th Vehicular Technology
Conference, Montreal, 25-28 September 2006, pp. 1-5.
[5] L. Ruiz de Temino, G. Berardinelli, S. Frattasi and P. Mo-
gensen, “Channel-Aware Scheduling Algorithms for
SCFDMA in LTE Uplink,” IEEE 19th International Sym-
posium on Personal, Indoor and Mobile Radio Communi-

I. AHMED ET AL. 494
cations, Cannes, 15-18 September 2008, pp. 1-6.
[6] C. Y. Ng and C. W. Sung, “Low Complexity Subcarrier
and Power Allocation for Utility Maximization in Uplink
OFDMA Systems,” IEEE Transactions on Wireless
Communications, Vol. 7, No. 5, 2008, pp. 1667-1675.
doi:10.1109/TWC.2008.060723.
[7] F. D. Calabrese, P. H. Michaelsen, C. Rosa, M. Anas, C.
U. Castellanos, D. L. Villa, K. I. Pedersen, P. E. Mogen-
sen, “Search-Tree Based Uplink Channel Aware Packet
Scheduling for UTRAN LTE,” IEEE Vehicular Technol-
ogy Conference, Singapore, 11-14 May 2008, pp.
1949-1953.
[8] E. Yaacoub and Z. Dawy, “A Game Theoretical Formu-
lation for Proportional Fairness in LTE Uplink Schedul-
ing,” IEEE Wireless Communications and Networking
Conference, Budapest, 5-8 April 2009, pp. 1-5.
[9] J. Huang, V. G. Subramanian, R. Agrawal and R. Berry,
“Joint Scheduling and Resource Allocation in Uplink
OFDM Systems for Broadband Wireless Access Net-
works,” IEEE Journal on Selected Areas in Communica-
tions, Vol. 27, No. 2, 2009, pp. 226-234.
doi:10.1109/JSAC.2009.090213
[10] H. G. Myung, J. S. Lim and D. J. Goodman, “Single Car-
rier FDMA for Uplink Wireless Transmission,” IEEE
Vehicular Technology Magazine, Vol. 1, No. 3, 2006, pp.
30-38. doi:10.1109/MVT.2006.307304
[11] A. Goldsmith, “Wireless Communications,” Oxford Uni-
versity Press, Oxford, 2005.
[12] J. S. Lim, H. G. Myung, K. J. Oh and D. J. Goodman,
“Proportional Fair Scheduling of Uplink Single-Carrier
FDMA Systems,” IEEE 17th International Symposium on
Personal, Indoor and Mobile Radio Communications,
Helsinki, 11-14 September 2006, pp. 1-6.