Received 12 March 2016; accepted 27 March 2016; published 30 March 2016

ABSTRACT

Motif discovery is one of the fundamental problems that have important applications in identifying drug targets and regulatory sites. Regulatory sites on DNA sequence normally correspond to shared conservative sequence patterns among the regulatory regions of correlated genes. These conserved sequence patterns are called motifs. Identifying motifs and corresponding instances is very important, so biologists can investigate the interactions between DNA and proteins, gene regulation, cell development and cell reaction under physiological and pathological conditions. In this work, we developed a motif finding algorithm based on a multi-objective genetic algorithm technique and incorporated the hypergeometric scoring function to enable it discover gapped motifs from organisms with challenging genomic structure such as the malaria parasite. The runtime performance of our resulting algorithm, EMOGAMOD (Extended Multi Objective Genetic Algorithm MOtif Discovery) was evaluated with that of some common motif discovery algorithms and the result was remarkable.

Keywords:

Genetic Algorithm, Motif Discovery, Multi-Objective Optimization

Subject Areas: Bioinformatics

1. Introduction

The discovery of patterns from a large data set remains a classical computer science problem. With the astronomical growth of biological databases, there is a need to extract useful information from the data stored in the various databases. Identification and discovery of patterns has been and still remains a concern to biologists and computer scientists as a result of the challenges inherent in developing efficient pattern discovery tools for these patterns. A motif refers to a sequence of characters or patterns hypothesized to have some biological importance. There are simple and gapped motifs. Simple motifs are made up of single patterns or words while gapped motifs are made up of several words with well defined gaps within a set of strings. For example, AATCGT is a simple DNA motif while AATCGTA----ACTGCA is a gapped motif consisting of two patterns of length seven and four gaps. A lot of researchers have been developing new algorithms for the analysis of genomic data with the aim of extracting useful information [1] [2] .

This work develops a motif discovery algorithm for identifying gapped motifs from organisms with peculiarity in their genomic structure such as the malaria parasite, Plasmoduim falciparum.

We adopted the high performance multi-objective genetic algorithm called NSGA II [1] and incorporated the hypergeometric scoring function for an enhanced tool capable of mining gapped motifs from the malaria parasite genome.

Plasmoduim falciparum is of particular interest because of the burden of malaria, which causes up to 2.7 million deaths per annum. In sub-Saharan Africa for instance, up to a staggering 90% of the malaria mortality recorded occurred in children population under the age of 5 years. [3] - [5] predicted that the incidence of malaria may increase by 50% within 20 years unless some new methods of eradication and control are devised In the post-genomic era, the ability to predict the behaviour, the function, or the structure of biological entities (such as genes and proteins), as well as interactions among them, play a major role in the discovery of information to help biologists explain biological mechanisms [5] - [8] .

The NSGA II used by EMOGAMOD to find a large number of tradeoff motifs with respect to conflicting objectives of similarity, motif length and support maximization resulted in discovering optimal motifs from a set of input genome. The use of the hypergeometric similarity check guaranteed the identification of gapped motifs from the AT-rich structure of the malaria parasite.

2. Methodology

The operating principle behind many motif discovery tools includes machine learning, pattern-driven and statistical techniques. Research has shown that tools based on a combination of techniques achieve better performance [4] [9] - [11] . This notion informed the architecture of EMOGAMOD which is a combination of machine learning and statistical technique.

EMOGAMOD proposes an extended algorithm for mining simple and gapped motifs particularly suited for organisms with peculiarity in their genomic structure. The malaria parasite, Plasmoduim falciparum has the peculiarity of a high incidence of the A and T nucleotides following each other making the genome AT-rich. A sample of the AT-rich genome of Plasmoduim falciparum is shown in Figure 1.

2.1. Architecture of EMOGAMOD

The architecture of EMOGAMOD is presented in Figure 2 with the logical flow of the processes involved depicted.

EMOGAMOG receives a list of DNA sequences as input, which contains unknown motifs that needs to be identified. A partition-based clustering technique is used to slide windows of fixed length L along the genome as this hypothetically represent a region where a k-mer appears several times in short succession. Our plan is to slide a window of fixed length L along the genome, looking for a region where a k-mer appears several times in

short succession. The parameter value L = 1000 reflects the typical length of a segment of the genome. A k-mer is defined as a “clump” if it appears many times within a short interval of the genome. More formally, given integers L and t, a k-mer Pattern forms an (L, t)-clump inside a (larger) string genome if there is an interval of genome of length L in which this k-mer appears at least t times. For example, TGCA forms a (25,3)-clump in the following Genome: gatcagcataagggtcccTGCAaTGCAtgacaagccTGCAgttgttttac. Then the sequences with a certain acceptable number of occurrences within each segment are extracted. This is followed by the computation of position weight matrix (PWM) which is a scoring matrix that shows the information content of the motifs, and depends on the frequency of occurrence of each of the characters in the identified pattern. Subsequently, the computation of the biological significance of the candidate motif is done by computing the similarity scores of the different motifs. The motifs with low similarity scores are reported as best optimal motifs.

The similar motifs, that is, those with one or two variations in the character that make up the motifs are merged using edit distance, before returning them as optimal motifs. The final output gives the optimal motifs.

2.2. Optimal Motif Extraction with Hyper-Geometric Scoring Function

EMOGAMOD implementation details involves the extraction of all unique words of 12 lengths occurring in the sequence space, this was done by outputting all unique motifs, then a p-value enrichment score is computed using a hyper-geometric formula shown below.

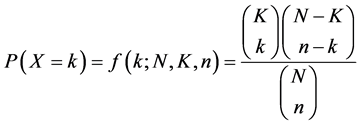
where k is the total set of genes, that is, positive and negative set, K a subset of the gene of interest, N is the total promoter sequence that matches the genes, n is the subset of the promoters which fall within the cluster of interest. The hyper-geometric formula is a standard statistical test used for gene enrichment analysis. It is a test that specifies whether a particular gene set is enriched for any functional annotations out of the full set of genes in the genome; the hyper-geometric p-value equals the probability of finding y matches of one randomly selected N genes out of the total k gene collection. The smaller the p-value scores for a candidate motif, the higher the likelihood of it being an optimal motif.

The computation result produced a long list of words with associated p-values representing the probability of word enrichment in the entire sequence. The next stage consist in listing the words in ascending order with the most enriched candidates (lowest p-values) serving to seed the construction of PWMs one at a time. The hash table data structure was used in implementing the sorting of the words with the aim of achieving an improved speed. All sequences differing from the seed word by one mismatch were then identified and re-listed by ascending p-value, before generating a PWM by individually weighing each word by its p-value score into the PWM.

The resulting PWM represents the probability of any given nucleotide occurring at a corresponding location in the candidate motif. The similarity of any sequence can be compared to the PWM through the calculation of a similarity score, which is the geometric mean of the corresponding matrix elements associated with the sequence. The similarity threshold selected determines the level of similarity that any given candidate motif must be to the PWM for it to be considered a true motif. The algorithm also adopts an optimal similarity threshold approach instead of using trial and error to guess the threshold for each candidate motif. This was achieved by first sorting all words by similarity to the PWM, then the p-values were re-calculated as more dissimilar words to the PWM were considered as motif instances using the hyper geometric scoring function and eventually identifying the similarity threshold that led to the lowest possible p-value. The entire process was repeated from the original seed word using two and three mismatches up to 40% of the word size to optimize mismatch levels in addition to similarity thresholds. The similarity and mismatch parameters that resulted in the lowest p-value were considered the best representation of a candidate motif. In addition, positional information using the edit distance metric was applied to merge non-unique motifs, thus preventing repeated sequences being represented as new motifs.

2.3. The EMOGAMOD GA Algorithm

The algorithm Input: Population size N;

Maximum number of generations G;

Crossover probability pc;

Mutation rate pm.

Output: Non dominated set.

Step 1: P: Initialize (P).

Step 2: while the termination criterion is not satisfied do.

Step 3: C: Select From (P).

Step 4: CI: Genetic Operators (C).

Step 5: P: Replace (PUCI).

Step 6: end while.

Step 7: return (P).

3. Results and Discussion

We applied the methodology described earlier to mine gapped motifs from the genome of Plasmoduim falciparum and compared the result with that of STGEMS.

3.1. Runtime Comparison of EMOGAMOD

The running time of EMOGAMOD compared with STGEMS and MOGAMOD tools is presented in Figure 3.

Five different sizes of genes were used in the analysis i.e. 5000, 10,000, 30,000, 40,000 and 60,000 characters, this variation in gene sizes is chosen to enable a classification of the performance of the algorithms as a function of input size. The empirical runtime of the different algorithms was obtained by including a time stamp at the beginning and end of execution of the algorithm so that its output displayed the execution time. From Figure 3, it is obvious that the run time of all the algorithms tested increased with respect to increase in the size of input.

3.2. EMOGAMOD and Mining Novel Motifs

EMOGAMOD was run using the 3D7 genes from Plasmoduim falciparum downloaded from PlasmoDB. A snapshot of some of the results is shown in Figure 4. This snapshot depicts the run of one of the modules of EMOGAMOD to extract unique motifs with their number of occurrences within the entire genome.

In order to validate the relevance of the motifs identified by EMOGAMOD, the STGEMS algorithm was used in running the same set of genes as a benchmark. This process of validation was hinged on the validation of the STGEMS algorithm with experimental methods. It can therefore be safely stated that the motifs identified by EMOGAMOD which were previously identified by STGEMS have been biologically validated. The biological relevance of the motif identified by EMOGAMOD can therefore be inferred based on its correlation with those identified by STGEMS.

In spite of the reported remarkable performance of MOGAMOD, EMOGAMOD outperformed MOGAMOD in terms of accuracy and runtime when tested with the same data set. Moreover, MOGAMOD could only identify motifs from other model organisms like yeast and bacteria but not from the malaria parasite, while EMOGAMOD identified ungapped and gapped motifs in these organisms.

4. Conclusions

We have developed a multi-objective genetic algorithm for the identification of gapped motifs in organisms, especially those with peculiarity in their genomic structure. These gapped motifs are biological elements such as gene promoters, regulatory element, and transcription factors which could be used as viable drug target to control the spread of disease causing organisms. The development of an effective tool for the identification of these elements in malaria parasite provides an insight into the complex genome of the organism and aims at the total eradication of malaria in Africa.

The study of regulatory elements such as transcription factors and DNA binding sites is important in knowledge discovery and understanding the life principles of organism and therefore an important area of research in Computational Biology.

Cite this paper

U. Angela Makolo,Salihu O. Suberu, (2016) Gapped Motif Discovery with Multi-Objective Genetic Algorithm. Open Access Library Journal,03,1-6. doi: 10.4236/oalib.1102293

References