Received 3 March 2016; accepted 20 March 2016; published 25 March 2016

ABSTRACT

By analytically solving a corrected balance between the force given by the Newton’s 2^nd law and the Newton gravitational force in polar coordinates, an equation for the intrinsic (i.e. two-body problem) perihelion precession of the planets of the solar system was obtained that when the Kepler’s 3^rd law is applied it coincides with the equation resulting from Einstein GTR.

Keywords:

Celestial Mechanics, Newtonian Gravitation, Newton’s 2^nd Law, Theory of Relativity, Perihelion Precession

Subject Areas: Classical Mechanics, Special Theory of Relativity

1. Introduction

The motivation of this paper was to find out if the modification to the balance between the force given by the Newton’s 2^nd law and the Newton gravitational force introduced in [1] , to account for the perihelion precession of Mercury, is applicable to the rest of the planets of the solar system. One importance of this work is that the differential equations obtained for the law of motion are very simple (when compared, for example, to the GTR) which could have a positive impact on the computational efficiency when solving more complicated problems (e.g. the N-body problem for evolution calculations). Other importance is related with the fact that the modification of the ODEs involves only the use of a power of the ubiquitous Lorentz factor which could suggests that a kind of extension of the special theory of relativity and/or electron theory to gravitational problems could be made without assuming more-difficult-to-measure concepts (e.g. a curved space-time). Another importance related with this work could be its potential impact on, for example, current or future gravitational problems or projects.

The correction to the balance between the force given by Newton’s 2^nd law and Newtonian gravitation, to account for the intrinsic perihelion precession of Mercury in 3D Cartesian geometry, introduced in [1] could be written, for the two-body problem with a static Sun, as

, , , ,

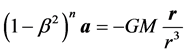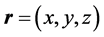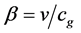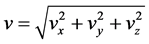
where

G is the Newton universal gravitational constant

M is the mass of the Sun

: The speed of the gravitational interaction (assumed to be equal to the speed of light in vacuum: c)

The equation of motion in the Heliocentric coordinate system [2] , considering that correction factor, is written as

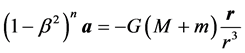(1)

Equation (1) was solved numerically in [1] , for n = +3, a rate of advance of the perihelion of Mercury was obtained in agreement with experiments. For n = −3 however the absolute value was also about 43"/sec but of negative sign.

When solving Equation (1) with n = −3 in polar coordinate it will be seen that the correct absolute value and sign of the perihelion precession of the planets is obtained.

The balance between the force given by Newton’s 2^nd law and Newtonian gravitation in polar coordinates.

Equation (1) in polar coordinates (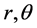) for a Newtonian (n = 0) balance, following [3] , is written as

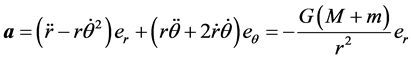(2)

From which the following differential equation is obtained 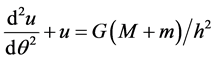[3] :

(3)

where 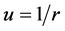and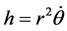: the angular momentum per unit mass, a constant.

The solution of an ODE of the type of Equation (3) is [4] :

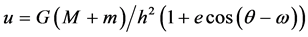(4)

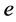and 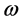are the constants of integration. Equation (4) is the equation of a conic section which includes the ellipse (Kepler 1^st law)

Equation (2) considering the correction factor of Equation (1) (using n = −3) can similarly be written as

(5)

Following the same approach used to obtain Equation (3) and considering that [5] , it is obtained:

(6)

,

The solution of Equation (6), considering that the multiplier of b represents a small perturbation to a solution expressed by Equation (4), can be expanded into Fourier series as [4]

Making use of trigonometric identities and neglecting terms containing 2^nd and higher power of:

,

, ,

Neglecting terms containing 2^nd and higher power of:

Substitute into Equation (6) and comparing coefficients of: expanding into Taylor/ Maclaurin series up to the linear term:.

The angle between two succeeding perihelion is [4] :

so

The precession of the perihelion per revolution is:

(7)

Considering that [6] , Equation (7) becomes:

The precession of the perihelion per orbital period is

(8)

Neglecting the mass of the planets in comparison to the mass of the Sun:

(9)

See the ratio of the mass of the planets to the mass of the Sun in the next section.

2. Computational Results and Analysis

The application of the Equation (9) to the planets of the solar system is given in Table 1 along with the results of the Einstein GTR (Equation (10)).

The Einstein GTR result of the precession per revolution is given by [7]

which when expressed per orbital period is,

(10)

The semi-major axis and the orbital period are taken from [8] . The eccentricity is taken from [3] except for Pluto that was taken from [6] .

From Table 1 it can be seen a remarkable agreement between and, which suggests a strong connection between them.

To find out that connection, the 3^rd law of Kepler expressed as [3] is substituted into Equation 9, it results in:

(11)

This is the equation used in the calculation of the precession shown in the last column of Table 1. When the Kepler’s 3^rd law is also substituted into Equation (10) (Einstein GTR), the Equation (11) is also obtained. So Equations (9) and (10) are equivalent when the orbital period is expressed in term of the semi-major axis.

If the mass of the planets is considered in S, h and in T, then Equations (9)-(11) become:

(12)

which results in a very small impact on Jupiter.

Note that the ratio of the mass of the planets to the mass of the Sun based on [9] is 1.660137E−7, 2.447840E−6, 3.040433E−6, 3.227149E−7, 9.547907E−4, 2.858776E−4, 4.355401E−5, 5.177591E−5, 7.692308E−9 for Mercury, Venus, Earth, …, Pluto respectively.

It is noted that if the number “3” in Equation (12) is replaced with L/2 where, the results are in close agreement with the values reported for Mercury in Table 1 of reference [1] for.

Equation (1) was solved numerically using n = 3 as in reference [1] . The results of the rate of the advance of the longitude of the perihelion () for Venus and Earth were 8.65"/cy and 3.83"/cy respectively which were determined from the slope of a linear fit of with time which had correlation coefficients (R²) greater than

0.95 (for Mercury R² was >0.9998). The simulation time was about 909 years forward and the integration step was 10⁻⁴ days. The set of points used for the orbital-elements calculation and for the fit were the set containing the calculated (from r(t) data) closest point to the Sun in each consecutive time interval of an orbital period. The mass of the planets and the initial conditions were taken from reference [9] .

Using the numerical approach just described, the solution of Einstein GTR equation of motion neglecting the mass of the planets [2] resulted in 8.58"/cy and 3.84"/cy for Venus and Earth respectively.

It could be worthy to perform experiments to find the value of n in for gravitational bound systems involving motions at very high speed and to find a fundament for this correction.

3. Concluding Remarks

An equation for the intrinsic (i.e. two-body problem) perihelion precession of the planets of the solar system was obtained based on the Fourier series solution of a corrected balance between the force given by the Newton’s 2^nd law and the Newton gravitational force in polar coordinates. When the Kepler’s 3^rd law is used to express the orbital period in term of the semi-major axis the perihelion precession equation coincides with the equation resulting from Einstein GTR.

Cite this paper

Barbaro Quintero-Leyva, (2016) On the Intrinsic Precession of the Perihelion of Planets of the Solar System. Open Access Library Journal,03,1-5. doi: 10.4236/oalib.1102554

References