Received 27 February 2016; accepted 12 March 2016; published 16 March 2016

ABSTRACT

The appropriateness measure of label expression is a basal concept in uncertainty modelling based on label semantics theory for dealing with vague concepts. In the paper, the concept of disjunctive normal forms is presented. It is proved that each label expression is semantic equivalent to a disjunctive normal form. Further, a new method of calculating the appropriateness measures of label expressions is provided.

Keywords:

Epistemic Vagueness, Label Semantics, Random sets, Appropriateness measure, Disjunctive Normal form

Subject Areas: Mathematical Analysis

1. Introduction

It is well known that any concept in classical mathematics is established on a crisp set (i.e., Cantor set). Suppose a concept Q is defined by a non-empty set D, then we say the statement that a is Q, is true (or its truth value is 1) if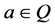; or else, it is false (or its truth value is 0). In other words, classical mathematics is established on classical logic or two-valued logic. However, for some propositions we cannot judge that they are true or false, such as the following propositions are not all classical propositions:

1) A coin tossed will be heads;

2) John will be in New York tomorrow;

3) John with 30 hairs is a bandicoot;

4) John is a bandicoot.

There are various nonclassical propositions in real life. Lukasiewicz is first extended classical logic to three- valued logic as early as 1920. In 1933, A.N. Kolmogoroff presented the probability theory for dealing with a type of uncertainty called randomness [1] (such as the above nonclassical propositions (1) and (2)). Following that, probabilistic logic for dealing with random proposition was proposed by Nilsson [2] based on probability theory in 1986. The theory of fuzzy set was initialized by Zadeh via membership function in 1965 [3] - [5] for fuzzy concepts (such as concept of bandicoot in the above propositions (3) and (4)). Following that, many types of many-valued logic and fuzzy logic were presented, respectively, such as Lukasiewicz fuzzy logic [6] product fuzzy logic, L logic [7] [8] , possibilistic logic [9] , BL logic [10] , and MTL logic [11] .

Although multi-valued logics, fuzzy logic [12] - [19] and probabilistic logic are well developed in theory aspect, an actual interpretation of truth value of proposition is controversial. For example, Elkan and Watkins oppose fuzzy logics [20] - [22] , and claim that fuzzy logics have some disadvantages, e.g., it does not hold the law of excluded middle (i.e.,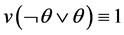) in classical logic, where denotes a proposition; 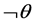denotes its negation of proposition; denotes disjunction; and 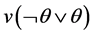denotes the truth value of proposition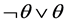. Recently, the author of paper also discussed this problem [23] .

In fact, Zadeh’s approach is the extension of a concept by a fuzzy set which has a graded characteristic or membership function with values between 0 and 1. This allows for intermediate membership (values in (0, 1)) in vague concepts resulting in intermediate truth values for propositions involving vague concepts (fuzzy logic). The calculus for fuzzy set theory is truth-functional which means that the full complement of Boolean laws cannot all be satisfied [24] . Furthermore, fuzzy set theory and fuzzy logic adopt an epistemic view of vagueness. Considering the shortcoming of fuzzy logic, it was proposed to the probabilistic logic holding the law of excluded middle dealing with fuzzy (or vague) concepts from a point of view in these papers [25] - [29] . In 2004, Lawry also provided a framework for linguistic modelling for dealing with vague (i.e. fuzzy) concepts based on label semantics using probability theory and random set [30] . At present it has been well developed [31] - [35] which was called uncertainty modelling for vague concepts in the paper [34] . In the theory, the appropriateness measure of label expressions is a basal concept. Given the label expression, a pivotal step of calculating the appropriateness measures is to seek a set of subsets of label corresponding to the label expression. Note that it is complicated to the approach of calculating the appropriateness measures of label expression provided in these papers [31] - [35] . Therefore the paper will discuss this problem.

The rest of this paper is organized as follows. Some basic concepts on uncertainty modelling for vague concepts are recalled in Section 2. In Section 3, the concept of disjunctive normal forms is first presented; then it is proved that each label expression is semantic equivalent to a disjunctive normal form; finally, a new method of calculating the appropriateness measure of label expression is provided. At the end of this paper, a brief summary is given.

2. Preliminaries

Definition 1 (Label expressions). Given a finite set of labels LA the corresponding set of label expressions LE is defined recursively as follows:

・ If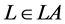, then;

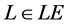・ If 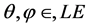then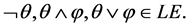

The mass function on sets of labels then quantifies the agent’s belief that any particular subset of labels contains all and only the labels with which it is appropriate to describe x i.e. is the agent's subjective probability that.

Definition 2 (Mass function on labels). a mass function on labels is a function such that.

Definition 3 (λ-mapping). is defined recursively as follows:

・

・

・

・

Based on the λ mapping we then define as the sum of over those set of labels in. The sum of over those set of labels in.

Definition 4 (Appropriateness measure). The appropriateness measure defined by mass function is a function satisfying

Let Val be the set of valuation functions where for means that is appropriate in the current context. In particular, the epistemic stance dictates that for each there would be a corresponding valuation (partially unknown to the agent) determining which labels are appropriate to describe x. A valuation naturally determines an extension defined recursively as follows: For and We can now define and as follows:

Definition 5.

・ if then.

・ if

・ θ is a tautology, if.

・ θ is a contradiction, if.

Theorem 6 (General properties of appropriateness measures). the following properties hold:

・ If then

・ then

・ If θ is a tautology, then

・ If θ is a contradiction, then

・ If is a contradiction, then

・

・ For, let then.

We not find the proof of last property in Theorem 6 in these papers [30] - [35] . Therefore, now we provide it.

Proof. Without loss of generality, suppose. Since it follows from Definition 3 that

Thus we only need to prove that

(2)

We first prove that

(3)

Since for each, , also, , and not holds, it follows that, and,. Therefore

Thus the formula (3) is true.

Now we prove that for any, if, then not holds. In fact, if E not contain, then not hold; if E contain then, not hold. In a word, not holds.

Therefore is true. It follows that

The theorem is proved.

3. Calculating of the appropriateness Measures

In the Section we first discuss the properties of valuation functions.

For convenience, we call each element in Label as atomic label expression. Let θ be a label expression containing atomic label expressions, then we can be denoted by. Although it not contains atomic label expressions, we also can write it as. The mapping is denoted by, and write For example, if, and then is regard as a vector in.

Note that is a subset of LA, and a relation of one to one from the set val of all this mapping to is gained, and the valuation function, of θ is a Boolean function. Such function f is denoted by. Where can be considered a random variable, a n-dimensional random variable, and a function of n random vari- ables.

Definition 7. A label expression θ is said to be a disjunctive normal form, if its form is

where is or, for and are all different.

Let, each is called a conjoint atomic label expression.

Lemma 8. For each, then where satis- fy that if if and for we have

Proof. Let

On the one hand, if it follows from that if Thus

On the other hand, let then there exists or is contained in and it is not contained in w. Suppose is contained in and it is not contained in w. Thus is contained in w and Thus

Lemma 9. Let label expression θ be a non-contradiction, and it contains atomic label expressions. Then it is semantically equivalent to a disjunctive normal form as follows:

,

i.e.,

,

where for each

satisfies that is if; is if, for

If

,

we call

,

as disjunctive normal form of θ, and it is denoted by.

Proof. From Definition 5 we need to prove

It is evident that we only need to prove iff

For suppose then by Lemma 8 we have It follows from conjoint atomic label expression is contained in

that thus

Contrarily, for suppose

By Lemma 8 we known that if. Thus is contain in

Thus

The theorem is proved.

By Lemma 9 and Definition 3 we easily gained the following Lemma.

Lemma 10. Let a mass function on labels LA is a function such that Then

if

where for each

satisfies that is if; is if, for

Theorem 11. Let a mass function on labels LA is a function such that For any

Proof. By Lemma 10 we have

It follows from Theorem 6 and the meaning of mapping, foe each, , thus the theorem is true.

Exempla 12. Suppose, , and is a mass function on labels LA satisfying:

For note that

It we write then

Thus we have

4. Conclusion

The paper manly provided a new method for calculating the appropriateness measures of label expressions. Based on the fact, each label expression is semantic equivalent to a disjunctive normal form.

Acknowledgements

This work was supported by national natural science foundation of China grant No.11471152 and No.61273044.

Cite this paper

Yang Liu,Xingfang Zhang, (2016) A New Method to Calculate the Appropriateness Measures of Label Expressions in Uncertainty Model. Open Access Library Journal,03,1-7. doi: 10.4236/oalib.1102399

References

NOTES

^*Corresponding author.