Open Access Library Journal
Vol.03 No.03(2016), Article ID:69076,13 pages
10.4236/oalib.1102432
Quantitative Structure Activity Relationship Analysis of Selected Chalcone Derivatives as Mycobacterium tuberculosis Inhibitors
Alisi Ikechukwu Ogadimma1*, Uzairu Adamu2
1Department of Applied Chemistry, Federal University, Dutsin-Ma, Nigeria
2Department of Chemistry, Ahmadu Bello University, Zaria, Nigeria

Copyright © 2016 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 February 2016; accepted 10 March 2016; published 14 March 2016

ABSTRACT
In order to gain further insights into the structural requirements for anti-tuberculosis activity by chalcone derivatives of 1,3-diphenylprop-2-ene-1-one, quantitative structure activity relationship (QSAR) was performed using genetic function approximation (GFA). Geometry optimization was achieved at the density functional theory (DFT) level using Becke’s three-parameter Lee-Yang- Parr hybrid functional (B3LYP) in combination with the 6-31G* basis set. Subsequently, quantum chemical and molecular descriptors were generated and divided into training and test sets by Kennard Stone algorithm. Internal and external validations as well as Y-randomization tests were employed in model validation. Five predictive models were generated by GFA. The generated models showed that constitutional indices, 2D autocorrelations and radial distribution function (RDF) descriptors were important contributors to anti-tuberculosis activity of 1,3-diphenylprop-2-ene-1-one derivatives. Based on validation results, model 4 was chosen as the best of the five models.
Keywords:
Anti-Tuberculosis, Descriptors, GFA, Model Validation, QSAR
Subject Areas: Theoretical Chemistry

1. Introduction
In recent time, there is an increasing concern over the re-emergence of tuberculosis (TB) which is an infectious diseases caused by the tubercle bacillus, Mycobacterium tuberculosis (M. tuberculosis). This re-emergence is attributed to the fact that TB is co-infected with the human immunodeficiency virus (HIV). Tuberculosis (TB) was the most common mycobacterial chronic communicable disease and in 2013, an estimated 9.0 million people developed TB and 1.5 million died from the disease, 360,000 of whom were HIV-positive [1] .
When a person is infected with Mycobacterium tuberculosis, the bacilli are thought to persist in a subclinical status with minimal replication, a status in which the bacteria are unable to cause or manifest clinical disease. Upon a shift in an individual’s immunologic status, M. tuberculosis is able to begin replicating and multiplying to a number that causes disease, manifesting as active TB [2] .
Active TB is diagnosed by evaluating an individual’s medical history, clinical symptoms, (chest) radiography, as well as the microbiologic and molecular identification of M. tuberculosis (through the detection of acid-fast bacilli insputum, M. tuberculosis culture, and nucleic acid amplification) [3] .
At present, compounds currently use for the treatment of tuberculosis due to their potent anti-tuberculosis activities include: para-amino salicylic acid (PAS), isoniazide (INH), rifampicin (RMP), pyrazinamide (PZA) and cycloserine [4] .
The emergence of multidrug resistant strains of Mycobacterium tuberculosis to clinically available drugs necessitates the need for the development of new compounds with potent anti-tuberculosis activities.
Computational procedures which employ cost effective evaluation of large virtual databases of chemical compounds are currently employed in the design of new drugs. Such procedures include Quantitative Structure-Activity Relationships (QSAR) models, Complex Networks theory, Artificial Neural Networks (ANN) analysis, Artificial Intelligence (AI) and Machine Learning (ML) [5] .
The QSAR paradigm is based on the assumption that there is an underlying relationship between the molecular structure and biological activity. On this assumption, QSAR attempts to establish a correlation between various molecular properties of a set of molecules with their experimentally known biological activity. The success of any QSAR model depends on accuracy of the input data, selection of appropriate descriptors and statistical tools and most importantly, validation of the developed model [6] .
In recent time, QSAR studies have been employed in order to explore the substitution requirements of synthesized compounds derivatives for their Mycobacterium tuberculosis inhibition activities. Such compounds include: 8-methylquinolones [7] ; 7-chloroquinoline derivatives [8] ; 3-heteroaryl-thioquinoline derivatives [9] ; β-thia adduct of chalconeanddiazachalcone derivatives [10] ; 5-nitrofuran-2-yl/4-nitrophenyl methylene substituted hydrazides [11] ; substituted benzothiazole/benzimidazole analogues [12] and biaryl analogues of PA-824 [13] .
Attention is currently drawn to the use of chalcone derivatives as anti-tuberculosis inhibitors. Umaa et al., in 2013 carried out QSAR studies on the anti-tuberculosis activity of chalcone derivatives by semi empirical AMI method. Model development is by multiple linear regression approach where log p and electronic energy are found to correlate with anti-mycobacterial activity of 1,3-diphenylprop-2-en-1-ones. Also [14] , in 2011 employed QSAR studies on a seriesof novel quinazolinone derivatives as anti-tubercular agents by semi empirical AMI Hamiltonian method using multiple linear regression analysis for model development. They observed that diameter, ovality, partition coefficient and radius are extremely significant for the design of new pharma-co- phores containing quinazolinone moiety for anti-tubercular activity.
In this study, a data set of twenty four chalcone derivatives of substituted 1,3-diphenylprop-2-en-1-ones were optimized at the density functional theory (DFT) level using Becke’s three-parameter Lee-Yang-Parr hybrid functional (B3LYP) in combination with the 6-31G* basis set. The optimized structures were employed in the generation of quantum chemical and molecular descriptors. These were then divided into training and test sets by Kennard Stone algorithm. The QSAR models were generated using the Genetic Function Approximation (GFA). The GFA technique is a conglomeration of Genetic Algorithm, Friedman’s multivariate adaptive regression splines (MARS) algorithm and Holland’s genetic algorithm to evolve population of equations that best fit the training set data [15] . A distinctive feature of GFA is that it produces a population of models, instead of generating a single model, as do most other statistical methods. The developed models were then subjected to internal and external validation and Y-randomization tests in order to establish their predictability and reliability.
This research on the anti-tuberculosis inhibition potentials of substituted 1,3-diphenylprop-2-en-1-ones generated results with higher levels of accuracy by employing higher levels of molecular optimization (DFT) and QSAR model development (GFA) methods in comparison to semi empirical and multiple linear regression methods used by [16] .
2. Materials and Methods
2.1. Data Set
A data set of twenty four substituted 1, 3-diphenyl prop-2-en-1-ones (Chalcone Derivatives) and their anti-my- cobacterium activities were obtained from the work of [17] . The anti-mycobacterium activities are represented by the IC50 value. The IC50 values were subjected to data transformation by taking the negative logarithm to the base of 10 according to the formula:

This is to ensure that a more uniformly distributed data is obtained.
The chemical structure of the compounds together with their experimental and predicted activities is shown in table 1.
The basic structure of 1,3-diphenylprop-2-ene-1-one is given by:
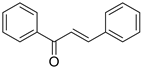
Table 1. Molecular structure with observed and predicted activity of chalcone derivatives used in training and test set.
2.2. Geometry optimization
Chemical structures of the compounds were drawn using the ChemDraw software [18] , while the molecular geometries were optimized using Spartan 14 software [19] , at the density functional theory (DFT) level using Becke’s three-parameter Lee-Yang-Parr hybrid functional (B3LYP) in combination with the 6-31G* basis set. The Spartan 14 software also resulted in the generation of a set of quantum chemical descriptors.
2.3. Descriptors calculation
The low energy conformers were then submitted for further generation of an additional set of molecular descriptors using the software “PaDel-Descriptor version 2.20”. Different physicochemical descriptors were calculated for each molecule in the study table. These descriptors included electronic, spatial, structural, thermodynamic and topological. This was combined to the set of quantum chemical descriptors obtained from the low energy conformer of the structures as generated by Spartan 14 software.
2.4. Data Pre-Treatment/Feature Selection
It is observed that constant value and highly correlated descriptors may cause difficulties in forming QSAR models, hence the predictivity and generalization of the model fails under these conditions.
In order to overcome this problem, the pre-processing for the generated molecular descriptors was done by removing descriptors having constant value and pairs of variables with correlation coefficient greater than 0.9 using “Data Pre-Treatment GUI 1.2” tool that uses V-WSP algorithm [20] [21] .
2.5. Creation of Training and Test Set
The dataset of twenty four molecular structures was split into training and test set by Kennard Stone algorithm technique using the software “Dataset Division GUI 1.2” [22] . This is an application tool used to perform rational selection of training and test set from the data set.
2.6. QSAR Model Development and Validation
2.6.1. Model Development
The QSAR model were developed from the training set compounds where the independent variables (quantum chemical and molecular descriptors) and the dependent (response) variable (pIC50) were subjected to multivariate analysis by Genetic Function Approximation (GFA) technique using the material studio software. GFA was performed by using 50,000 crossovers, a smoothness value of 1.00 and other default settings for each combination. An initial of three and a maximum of five terms per equation were considered for model development.GFA measures the fitness of a model during the evolution process by calculating the Friedman lack-of-fit (LOF). In Materials Studio, LOF is calculated using the expression:
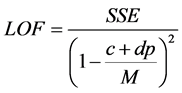
where SSE is the sum of squares of errors, c is the number of terms in the model, other than the constant term, d is a user-defined smoothing parameter, p is the total number of descriptors contained in all model terms (again ignoring the constant term) and M is the number of samples in the training set [23] .
2.6.2. Model Validation
The developed QSAR models were validated in order to test the internal stability and predictive ability of the models. The procedure employed in model validation is:
1) Internal Model Validation
The developed models were validated internally by leave-one-out (LOO) cross-validation technique. In this technique, one compound is eliminated from the data set at random in each cycle and the model is built using the rest of the compounds. The model thus formed is used for predicting the activity of the eliminated compound. The process is repeated until all the compounds are eliminated once.
The cross-validated squared correlation coefficient, 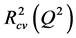 was calculated using the expression:
was calculated using the expression:
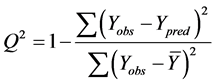
where 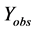 represents the observed activity of the training set compounds,
represents the observed activity of the training set compounds, 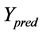 is the predicted activity of the training set compounds and
is the predicted activity of the training set compounds and  corresponds to the mean observed activity of the training set compounds.
corresponds to the mean observed activity of the training set compounds.
Also calculated was the adjusted r2 (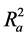 ) which is a modification of r2 that adjusts for the number of explanatory terms in a model. Unlike r2 in which addition of descriptors to the developed QSAR model increases its value, the value of
) which is a modification of r2 that adjusts for the number of explanatory terms in a model. Unlike r2 in which addition of descriptors to the developed QSAR model increases its value, the value of 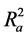 increases only if the new term improves the model more than what would be expected by chance [24] .
increases only if the new term improves the model more than what would be expected by chance [24] .
Hence 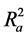 overcomes the draw backs associated with the value of r2 and was calculated using the expression:
overcomes the draw backs associated with the value of r2 and was calculated using the expression:
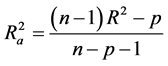
where p is the number of predictor variables used in the model development.
In other to judge the overall significance of the regression coefficients, the variance ratio, F value (the ratio of regression mean square to deviations mean square), was also calculated using the relation:
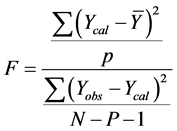
2) External Model Validation
External validation was employed in order to determine the predictive capacity of the developed model as judged by its application for the prediction of test set activity values and calculation of predictive R2 (R2 pred) value as given by the expression:
where 



It has been observed that 
value is controlled by

reflect the predictive capability of the developed model with regard to a new data set [25] . This may result in considerable numerical difference between the observed and predicted values in spite of maintaining a good overall intercorrelation.
A modified r2 called 
where 






When the axes are interchanged, i.e. predicted values are considered in y-axis and observed values are considered in the x-axis, we obtain the parameter 




All the external validation parameters were generated using the program: External Validation Metric Calculator “DTC-MLR Plus Validation GUI 1.2” [28] - [31] .
3) Randomization Test
The robustness of the developed QSAR model was checked using the Y-randomization technique in which model randomization was employed. In Y-randomization, validation was performed by permuting the response values, Activity (Y) with respect to the descriptor (X) matrix which was unaltered [32] .
The deviation in the values of the squared mean correlation coefficient ofthe randomized model (
In an ideal case, it is observed that the average value of 


In other to penalize the developed models for the difference between the squared correlation coefficients of the randomized and the non-randomized models, the value 
The Y-randomization results were generated using the program “MLR Y-Randomization Test 1.2” [35] .
3. Results and Discussion
3.1. Geometry Optimization and Descriptors Calculation
The observed activities for the various data sets were transformed to obtain a more uniformly distributed data as shown in table 1. After minimization of the various compounds in the data set 32 descriptors were generated using the Spatans 14 software. These were combined to the 1875 descriptors generated using the PaDEL software to give a total of 1907 descriptors.
3.2. Feature Selection and Data Division
The generated descriptor results were subjected to data pre-treatment where descriptors having constant value and pairs of variables with correlation coefficient greater than 0.9 were removed using the software: “Data Pre-Treatment GUI 1.2”. Data pre-treatment resulted in 973 descriptors from 1907descriptors, thus removing 934 invariable and highly correlated descriptors.
Data division using Dataset Division GUI 1.2” tool resulted in 16 molecular compounds (comprising approximately 67% of total compounds) in the training set and 8 compounds (comprising approximately 33.3% of total compounds) in the test set.
3.3. Model Development and Validation
A total of five models were developed from the training set by Genetic Function Approximation using the Material Studio Software. The developed models and the description of the molecular descriptors which appeared in the developed models are given in table 2 and table 3 respectively.
The predicted activities of the training set compounds by the developed models were also generated by the Material Studio Software as shown in table 4 andtable 5.
The results of the internal validation for the developed models are given in table 6.
Table 2. Developed models using genetic function approximation.
Table 3. Description of the molecular descriptors which appeared in the developed models.
Table 4. Predicted activities of the training set by the developed model.
Average Activity for Training Set: 6.494366.
The external validation results are summarized in table 7. The five models passed the Golbraikh and Tropsha acceptable criteria for model predictability. According to this criteria, a QSAR model is predictive if:





Table 5. Actual and predicted activities for the test set.
Table 6. Internal validation results for the generated models by genetic function approximation.
Table 7. Comparison of statistical qualities and external validation parameters of the various models.
If we consider the predictive capacity of the developed models, model 3 has the best predictive capacity since it has the highest 






The results of Y-randomization test for the developed models have 

Model 4 which is given by:
pIc50 = −2.040810634 * nCl − 19.024890361 * MATS2m + 1.855704759 * RDF140s + 6.739013671 was chosen as the best of the five models based on the excellent results obtained from the statistical validation parameters. The graph of correlation between observed activity and predicted activity of Training Set compounds using model 4 are given in figure 1. Also the graph of correlation between observed activity and predicted activity of Test Set compounds using model 4 are given in figure 2.
Figure 1. The graph of correlation between observed activity and predicted activity of Training Set compounds using model 4.
Figure 2. The graph of correlation between observed activity and predicted activity of test set compounds using model 4.
3.4. Interpretation of the descriptors in the QSAR equations
The descriptors which contributed to the specific anti-tuberculosis inhibitory activity in the selected model and their importance are discussed below:
Equations 1 to 5 showed the importance of nCl, MATS2m, GATS1m, RDF115e, RDF115u, RDF130m and RDF140s descriptors, on the anti-tuberculosis activity of 1,3-diphenylprop-2-ene-1-ones. From the developed models the descriptors nCl, MATS2m, GATS1m, RDF115e and RDF115u correlate negatively with the anti-bacteria biological activities of 1,3-diphenylprop-2-ene-1-one derivatives while the descriptors RDF130m and RDF140s correlates positively with the activities. This suggests that lower values of the descriptors nCl, MATS2m, GATS1m, RDF115e and RDF115u and higher values of the descriptors RDF130m and RDF140s lead to improvements in Anti-tuberculosis inhibitory activity.
In the developed models, four Radial Distribution Function (RDF) descriptors are encountered namely RDF115u, RDF115e, RDF130m and RDF140s. The RDF descriptors are based on a radial distribution function which can be interpreted as the probability distribution of finding an atom in a spherical volume of radius r [38] .
For a Radial Distribution Function defined by RDFrw, which is generally calculated at a number of discrete points with a step size for r = 0.5 Å under five different weighing schemes (w), given by the unweighted case (u), atomic mass (m), Van der Waals volume (v), atomic polarizability (p) and Sanderson atomic electronegativity (e). Besides information about interatomic distances in the entire molecule, RDF descriptors provide further valuable information, for example, about bond distances, ring types, planar and non-planar systems and atom types [39] .
Among the four RDF descriptors in the developed models, one is unweighted, the second is weighted by atomic Sanderson electronegativity, the third is weighted by atomic masses, while the remaining one descriptor is weighted by one-state.
Since the descriptor nCl is negatively correlated with anti-tuberculosis activity of 1,3-diphenylprop-2-ene- 1-ones, the presence of a chlorine substituent in the chalcone derivative does not improve the anti-tuberculosis activity of 1,3-diphenylprop-2-ene-1-ones. This is also confirmed by the descriptor RDF115e which is also negatively correlated with anti-tuberculosis activity for the considered derivatives.
MATS2m (Moran autocorrelation-lag 2/weighted by atomic masses) and GATS1m (Geary autocorrelation of lag 1 weighted by mass) are 2D autocorrelation descriptors, which are obtained from molecular graphs, by summing the products of atom weights of the terminal atoms of all the paths of the considered path length (the lag) [40] . These descriptors are related to the atomic property of a molecule, such as molecular size influence the retention of compound. Since MATS2m and GATS1m are negatively correlated with anti-tuberculosis activity, their decrease has a positive influence on the anti-tuberculosis activity of 1,3-diphenylprop-2-ene-1-ones.
This result illustrates that the proper distribution of the above properties is a necessary requirement for chalcone derivatives of 1,3-diphenyl prop-2-en-1-ones with potent anti-tuberculosis activity.
4. Conclusions
In this research, the ant-tuberculosis inhibition potentials of twenty four molecular structures of chalcone derivatives of 1,3-diphenylprop-2-ene-1-one were modelled by QSAR. Geometry optimization was investigated at the DFT level. The optimized structures were submitted for the generation of a total number of 1907 quantum chemical and molecular descriptors which were further subjected to data pre-treatment. The entire data set was split into training and test sets by Kennard Stone algorithm. Model development was achieved by Genetic Function Approximation which resulted in the generation of five models.
Based on this present QSAR studies, it was observed that the descriptors which were highly correlated with the anti-bacteria biological activity of 1,3-diphenylprop-2-ene-1-one derivatives were: nCl, MATS2m, GATS1m, RDF115e, RDF115u, RDF130m and RDF140s descriptors. From the developed model, the descriptors nCl, MATS2m, GATS1m, RDF115e and RDF115u correlated negatively with the anti-bacteria biological activities of 1,3-diphenylprop-2-ene-1-one derivatives while the descriptors RDF130m and RDF140s correlated positively with the activities.
This research strongly suggested that the main features controlling ant-tuberculosis inhibition activities of chalcone derivatives of 1,3-diphenylprop-2-ene-1-one were constitutional indices, 2D autocorrelations and Radial Distribution Function (RDF) descriptors. In comparison to the QSAR studies of 1,3-diphenylprop-2- ene-1-one derivatives conducted by Umaa et al., in 2013 only log p and electronic energy were found to contribute to anti-tuberculosis activity. Also higher levels of accuracy were attained in this research such as an R2 value of 0.94801500, compared to 0.898421 obtained by [15] . The developed five models passed all the Golbraikh and Tropsha acceptable criteria for model predictability as given in Table 7.
On the basis of the developed QSAR models, novel 1,3-diphenylprop-2-ene-1-one derivatives could be designed as potential anti-tuberculosis agents.
Cite this paper
Alisi Ikechukwu Ogadimma,Uzairu Adamu, (2016) Quantitative Structure Activity Relationship Analysis of Selected Chalcone Derivatives as Mycobacterium tuberculosis Inhibitors. Open Access Library Journal,03,1-13. doi: 10.4236/oalib.1102432
References
- 1. World Health Organization (WHO) (2014) Global Tuberculosis Report.
- 2. Mack, U., Migliori, G.B., Sester, M., Rieder, H.L., Ehlers, S., Goletti, D., Bossink, A., Magdorf, K., Holscher, C., Kampmann, B., Arend, S.M., Detjen, A., Bothamley, G., Zellweger, J.P., Milburn, H., Diel, R., Ravn, P., Cobelens, F., Cardona, P.J., Kan, B., Solovic, I., Duarte, R., Cirillo, D.M. and Lange, C. for the TBNET (2009) LTBI: Latent Tuberculosis Infection or Lasting Immune Responses to M. Tuberculosis? ATBNET Consensus Statement. European Respiratory Society, 33, 956-973.
http://dx.doi.org/10.1183/09031936.00120908 - 3. European Centre for Disease Prevention and Control. (2011) Use of Interferon-Gamma Release Assays in Support of TB Diagnosis. ECDC, Stockholm.
- 4. Tripathi, R., Tewari, N., Dwivedi, N. and Tiwari, V.K. (2005) Fighting Tuberculosis: An Old Disease with New Challenges. Medicinal Research Reviews, 25, 93-131.
http://dx.doi.org/10.1002/med.20017 - 5. Alejandro, S.P., Marcus Tulius, S. and de Paulo-Emerenciano, V. (2010) Current Pharmaceutical Design of Antituberculosis Drugs: Future Perspectives. Current Pharmaceutical Design, 16, 2656-2665.
http://dx.doi.org/10.2174/138161210792389289 - 6. Ibezim1, E.C., Duchowicz, P.R., Ibezim, N.E., Mullen, L.M.A., Onyishi, I.V., Brown, S.A. and Castro, E.A. (2009) Computer-Aided Linear Modeling Employing QSAR for Drug Discovery. Scientific Research and Essay, 4, 1559-1564.
- 7. Eric, G.M., Uzairu, A. and Mamza, P.A.P. (2015) Investigation of the Activity of 8-Methylquinolones against Mycobacterium tuberculosis Using Theoretical Molecular Descriptors: A Case Study. European Scientific Journal September, 11, 1857-7881.
- 8. Ravichandran, V., Shalini, S., Sokkalingam, A.D., Harish, R. and Suresh, K. (2014) QSAR Study of 7-Chloroquinoline Derivatives as Antitubercular Agents. World Journal of Pharmacy and Pharmaceutical Sciences, 3, 1072-1082.
- 9. Ravichandran, V., Shalini, S., Kumar, K.V., Harish, R. and Kumar, K.S. (2015) QSAR Study on Arylthioquinoline Derivatives as Anti-Tubercular Agents. PTB Reports, 1, 81-86.
http://dx.doi.org/10.5530/PTB.1.2.8 - 10. Younes, A., Abdelkader, A., Hayat, L., Ahmed, R., Driss, Z. and Mohamed, Z. (2014) QSAR for Antimycobacterial Activity of β-Thia Adduct of Chalcone and Diazachalcone Derivatives. International Journal of Computational and Theoretical Chemistry, 2, 20-25.
http://dx.doi.org/10.11648/j.ijctc.20140203.11 - 11. Gupta, R.A. and Kaskhedikar, S.G. (2012) Synthesis, Evaluation and QSAR Analysis of 5-Nitrofuran-2-Yl/4-Nitrophenyl Methylene Substituted Hydrazides as Antitubercular Agents. Asian Journal of Pharmaceutical and Clinical Research, 5, 251-259.
- 12. Priyadarsini, R., Tharanib, C.B., Sathya, S. and Kavithaa, S. (2012) Pharmacophore Modeling and 3D-QSAR Studies on Substituted Benzothiazole/Benzimidazole Analogues as DHFR Inhibitors with Antimycobacterial Activity. International Journal of Pharma Sciences and Research, 3, 4441-4450.
- 13. Sawarkar, V.M., Dudhe, P.B., Nagras, M.A., Bhosle, P.V., Jadhav, B. and Meshram, R.S. (2013) 2D & 3D QSAR Studies of Biaryl Analogues of Pa-824 Having Various Ether Linkers: An Approach to Design Antitubercular Agents. Pharmacophore, 4, 92-104.
- 14. Rajasekaran, S., Gopalkrishna, R. and Sanjay, P.P.N. (2011) 2D QSAR Studies of Some Novel Quinazolinone Derivatives as Antitubercular Agents. Journal of Computational Methods in Molecular Design, 1, 69-82.
- 15. Kamalakaran, A.S., Srinivasan, S. and Veluchamy, A. (2009) QSAR Studies on N-Aryl Derivative Activity towards Alzheimer’s Disease. Molecules, 14, 1448-1455.
http://dx.doi.org/10.3390/molecules14041448 - 16. Umaa, K., Kavithamani, A., Maida Engels, S.E. and Geetha, G. (2013) Quantitative Structure Activity Studies on the Anti-Mycobacterial Potentials of Certain Chalcone Derivatives. International Journal of Research in Organic Chemistry, 3, 6-10.
- 17. Lin, Y.M., Zhou, Y., Flavin, M.T. and Zhou, L.M. (2002) Chalcones and Flavonoids as Anti-Tuberculosis Agents. Bioorganic & Medicinal Chemistry, 10, 2795-2802.
http://dx.doi.org/10.1016/S0968-0896(02)00094-9 - 18. ChemBioDraw version 12.0. CambridgeSoft, 2010.
- 19. Spartan 14v112 (2013) Wavefunction, Inc., Irvine.
- 20. Ballabio, D., Consonni, V., Mauri, A., Claeys-Bruno, M., Sergent, M. and Todeschini, R. (2014) A Novel Variable Reduction Method Adapted from Space-Filling Designs. Chemometrics and Intelligent Laboratory Systems, 136, 147-154.
http://dx.doi.org/10.1016/j.chemolab.2014.05.010 - 21. Ambure, P., Aher, R.B., Gajewicz, A. and Puzyn, T. (2015) “NanoBRIDGES” Software: Open Access Tools to Perform QSAR and Nano-QSAR Modeling. Chemometrics and Intelligent Laboratory Systems, 147, 1-13.
http://dx.doi.org/10.1016/j.chemolab.2015.07.007 - 22. Todd, M.M., Harten, P., Douglas, M.Y., Muratov, E.N., Golbraikh, A., Zhu, H. and Tropsha, A. (2012) Does Rational Selection of Training and Test Sets Improve the Outcome of QSAR Modeling? Journal of Chemical Information and Modeling, 52, 2570-2578.
http://dx.doi.org/10.1021/ci300338w - 23. Khaled, K.F. and Abdel-Shafi, N.S. (2011) Quantitative Structure and Activity Relationship Modeling Study of Corrosion Inhibitors: Genetic Function Approximation and Molecular Dynamics Simulation Methods. International Journal of Electrochemical Science, 6, 4077-4094.
- 24. Das, R.N. and Roy, K. (2012) Development of Classification and Regression Models for Vibrio fischeri Toxicity of Ionic Liquids: Green Solvents for the Future. Toxicology Research, 1, 186-195.
http://dx.doi.org/10.1039/c2tx20020a - 25. Kar, S. and Roy, K. (2011) Development and Validation of a Robust QSAR Model for Prediction of Carcinogenicity of Drugs. Indian Journal of Biochemistry and Biophysics, 48, 111-122.
- 26. Roy, P.P. and Roy, K. (2008) On Some Aspects of Variable Selection for Partial Least Squares Regression Models. QSAR & Combinatorial Science, 27, 302-313.
http://dx.doi.org/10.1002/qsar.200710043 - 27. Indrani, M., Achintya, S. and Kunal, R. (2010) Chemometric Modeling of Free Radical Scavenging Activity of Flavone Derivatives. European Journal of Medicinal Chemistry, 45, 5071-5079.
http://dx.doi.org/10.1016/j.ejmech.2010.08.016 - 28. Roy, K. and Mitra, I. (2011) On Various Metrics Used for Validation of Predictive QSAR Models with Applications in Virtual Screening and Focused Library Design. Combinatorial Chemistry & High Throughput Screening, 14, 450-474.
http://dx.doi.org/10.2174/138620711795767893 - 29. Roy, K., Chakraborty, P., Mitra, I., Ojha, P.K., Kar, S. and Das, R.N. (2013) Some Case Studies on Application of “rm2” Metrics for Judging Quality of Quantitative Structure-Activity Relationship Predictions: Emphasis on Scaling of Response Data. Journal of Computational Chemistry, 34, 1071-1082.
http://dx.doi.org/10.1002/jcc.23231 - 30. Golbraikh, A. and Tropsha, A. (2002) Beware of q2! Journal of Molecular Graphics and Modelling, 20, 269-276.
http://dx.doi.org/10.1016/S1093-3263(01)00123-1 - 31. Tropsha, A. (2010) Best Practices for QSAR Model Development, Validation, and Exploitation. Molecular Informatics, 29, 476-488.
http://dx.doi.org/10.1002/minf.201000061 - 32. Roy, K., Kar, S. and Das, R.N. (2015) Statistical Methods in QSAR/QSPR. In: Roy, K., Kar, S. and Das, R.N., Eds., A Primer on QSAR/QSPR Modeling, Springer Briefs in Molecular Science, Springer, Berlin, 37-59.
http://dx.doi.org/10.1007/978-3-319-17281-1_2 - 33. Roy, K. and Paul, S. (2008) Exploring 2D and 3D QSARs of 2,4-diphenyl-1,3-oxazolines for Ovicidal Activity against Tetranychus urticae. QSAR & Combinatorial Science, 28, 406-425.
http://dx.doi.org/10.1002/qsar.200810130 - 34. Todeschini, R. (2010) Milano Chemometrics. Italy (Personal Communication).
- 35. Pravin, A. (2013) Drug Theoretics & Cheminformatics (DTC) Laboratory, Jadavpur University.
- 36. Partha, P.R., Somnath, P., Indrani, M. and Kunal, R. (2009) On Two Novel Parameters for Validation of Predictive QSAR Models. Molecules, 14, 1660-1701.
http://dx.doi.org/10.3390/molecules14051660 - 37. Roy, K. (2007) On Some Aspects of Validation of Predictive Quantitative Structure-Activity Relationship Models. Expert Opinion on Drug Discovery, 2, 1567-1577.
http://dx.doi.org/10.1517/17460441.2.12.1567 - 38. Singh, P. (2013) Molecular Descriptors in Modelling of TNF-∝ Converting Enzyme (TACE) Inhibition Activity of 2-(2-Aminothiazol-4-yl) pyrrolidine-Based Tartrate Diamides. Indian Journal of Chemistry, 52, 1325-1341.
- 39. Cheng, Z.J. and Zhang, Y.T. (2010) Classification Models of Estrogen Receptor-β Ligands Based on PSO-Adaboost-SVM. Journal of Convergence Information Technology, 5, 67-83.
http://dx.doi.org/10.4156/jcit.vol5.issue2.8 - 40. Fernandez, M., Caballero, J. and Tundidor-Camba, A. (2006) Linear and Nonlinear QSAR Study of N-hydroxy-2-[(phenylsulfonyl)amino] Acetamide Derivatives as Matrix Metalloproteinase Inhibitors. Bioorganic & Medicinal Chemistry, 14, 4137-4150.
http://dx.doi.org/10.1016/j.bmc.2006.01.072
NOTES
*Corresponding author.










