Received 18 February 2016; accepted 4 March 2016; published 9 March 2016

ABSTRACT

A sufficient condition in terms of lower cut sets is given for the insertion of a continuous function between two comparable real-valued functions.

Keywords:

Weak Insertion, Strong Binary relation, C-open Set, Semi-Preopen set, α-open Set, Lower Cut set

Subject Areas: Topology

1. Introduction

The concept of a C-open set in a topological space was introduced by E. Hatir, T. Noiri and S. Yksel in 1996 [1] . The authors define a set s to be a C-open set if, where u is open and A is semi-preclosed. A set s is a C-closed set if its complement is C-open set or equivalently if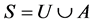, where u is closed and A is semi-preopen. The authors show that a subset of a topological space is open if and only if it is an α-open set and a C-open set. This enable them to provide the following decomposition of continuity: a function is continuous if and only if it is α-continuous and C-continuous.

Recall that a subset A of a topological space 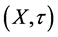is called α-open if A is the difference of an open and a nowhere dense subset of X. A set A is called α-closed if its complement is α-open or equivalently if A is union of a closed and a nowhere dense set. Sets which are dense in some regular closed subspace are called semi-preopen or β-open. A set is semi-preclosed or β-closed if its complement is semi-preopen or β-open.

The concept of a set A was β-open if and only if 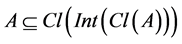was introduced by J. Dontchev in 1998 [2] .

Recall that a real-valued function f defined on a topological space x was called A-continuous if the preimage of every open subset of 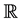belongs to A, where A was a collection of subset of x and this the concept was introduced by M. Przemski in 1993 [3] . Most of the definitions of function used throughout this paper are consequences of the definition of A-continuity. However, for unknown concepts, the reader might refer to papers introduced by J. Dontchev in 1995 [4] , M. Ganster and I. Reilly in 1990 [5] .

Hence, a real-valued function f defined on a topological space x is called c-continuous (resp. α-continuous) if the preimage of every open subset of 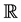is c-open (resp. α-open) subset of x.

Results of Katĕtov in 1951 [6] and in 1953 [7] concerning binary relations and the concept of an indefinite lower cut set for a real-valued function, which was due to Brooks in 1971 [8] , were used in order to give necessary and sufficient conditions for the strong insertion of a continuous function between two comparable real-valued functions.

If g and f are real-valued functions defined on a space X, we write 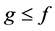in case 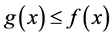for all x in X.

The following definitions were modifications of conditions considered in paper introduced by E. Lane in 1976 [9] .

A property p defined relative to a real-valued function on a topological space is a c-property provided that any constant function has property p and provided that the sum of a function with property p and any continuous function also has property p. If 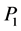and 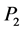are c-property, the following terminology is used: A space x has the weak c-insertion property for 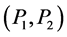if and only if for any functions g and f on x such that 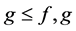has property 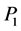and f has property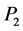, then there exists a continuous function h such that.

In this paper, it is given a sufficient condition for the weak c-insertion property. Also several insertion theorems are obtained as corollaries of this result.

2. The Main Result

Before giving a sufficient condition for insertability of a continuous function, the necessary definitions and terminology are stated.

Let be a topological space, the family of all α-open, α-closed, C-open and C-closed will be denoted by, , and, respectively.

Definition 2.1. Let a be a subset of a topological space. Respectively, we define the α-closure, α-interior, C-closure and C-interior of a set a, denoted by and as follows:

Respectively, we have are α-closed, semi-preclosed and are α-open, semi-preopen.

The following first two definitions are modifications of conditions considered in [6] [7] .

Definition 2.2. If ρ is a binary relation in a set S then is defined as follows: if and only if implies and implies for any u and v in S.

Definition 2.3. A binary relation ρ in the power set of a topological space x is called a strong binary relation in in case ρ satisfies each of the following conditions:

1) If for any and for any, then there exists a set C in such that and for any and any.

2) If, then.

3) If, then and.

The concept of a lower indefinite cut set for a real-valued function was defined [8] as follows:

Definition 2.4. If f is a real-valued function defined on a space x and if for a real number, then is called a lower indefinite cut set in the domain of f at the level.

We now give the following main result:

Theorem 2.1. Let g and f be real-valued functions on a topological space x with. If there exists a strong binary relation ρ on the power set of x and if there exist lower indefinite cut sets and in the domain of f and g at the level t for each rational number t such that if then, then there exists a continuous function h defined on X such that.

Proof. Let g and f be real-valued functions defined on x such that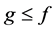. By hypothesis there exists a strong binary relation ρ on the power set of x and there exist lower indefinite cut sets and in the domain of f and g at the level t for each rational number t such that if then.

Define functions F and g mapping the rational numbers into the power set of X by and. If and are any elements of with, then, and. By Lemmas 1 and 2 of [7] it follows that there exists a function h mapping into the power set of X such that if and are any rational numbers with, then and.

For any x in x, let.

We first verify that: If x is in then x is in for any; since x is in implies that, it follows that. Hence. If x is not in, then x is not in for any; since x is not in implies that, it follows that. Hence.

Also, for any rational numbers and with, we have. Hence is an open subset of X, i.e., h is a continuous function on x.

The above proof used the technique of proof of Theorem 1 of [6] .

3. Applications

The abbreviations and are used for α-continuous and c-continuous, respectively.

Corollary 3.1. If for each pair of disjoint α-closed (resp. c-closed) sets of X , there exist open sets and of X such that, and then X has the weak c-insertion property for (resp.).

Proof. Let g and f be real-valued functions defined on the X, such that f and g are (resp.), and. If a binary relation ρ is defined by in case (resp.), then by hypothesis ρ is a strong binary relation in the power set of x. If and are any elements of with, then

since is an α-closed (resp. c-closed) set and since is an α-open (resp. c-open) set, it follows that (resp.). Hence implies that. The proof follows from Theorem 2.1.

Corollary 3.2. If for each pair of disjoint α-closed (resp. c-closed) sets, there exist open sets and such that, and then every α-continuous (resp. c-continuous) function is continuous.

Proof. Let f be a real-valued α-continuous (resp. c-continuous) function defined on the X. Set, then by Corollary 3.1, there exists a continuous function h such that.

Corollary 3.3. If for each pair of disjoint subsets of X , such that is α-closed and is C-closed, there exist open subsets and of X such that, and then x have the weak c-insertion property for and.

Proof. Let g and f be real-valued functions defined on the X, such that g is ac (resp.) and f is (resp. ac), with. If a binary relation ρ is defined by in case (resp.), then by hypothesis ρ is a strong binary relation in the power set of X. If and are any elements of with, then

since is a c-closed (resp. α-closed) set and since is an α-open (resp. c-open) set, it follows that (resp.). Hence implies that. The proof follows from Theorem 2.1.

Acknowledgements

This research was partially supported by Centre of Excellence for Mathematics(University of Isfahan).

Cite this paper

Majid Mirmiran, (2016) Weak Insertion of a Continuous Function between Two Comparable α-Continuous (C-Continuous) Functions. Open Access Library Journal,03,1-4. doi: 10.4236/oalib.1102453

References

NOTES

^*This work was supported by University of Isfahan and Centre of Excellence for Mathematics (University of Isfahan).