Received 13 February 2016; accepted 28 February 2016; published 3 March 2016

ABSTRACT

It is generally accepted that dark matter must be found throughout galaxies. The observed motion of stars demands that galaxies contain large amounts of dark matter distributed throughout according to a particular density function. However, it is argued in this paper that this assumed density function should apply to all matter in the galaxy, not just dark matter. This paper reasons that in a region where a strong concentration of visible matter is observed, an absence of dark matter ought to be expected. In particular, calculations show that the dark matter density in the expanded solar neighbourhood (a kiloparsec radial extent from the Sun) should be as expected, in agreement with kinematic measurements; however, the immediate solar neighbourhood (within a few parsecs radial extent from the Sun) should be mostly devoid of dark matter, in accordance with the lack of success in finding dark matter using direct detection experiments on Earth.

Keywords:

Galaxy: structure―solar Neighborhood, Galaxies: Dark matter, mass and Mass distribution, Kinematics and dynamics

Subject Areas: Modern Physics, Theoretical Physics

1. Introduction

It is widely accepted that a dominant fraction of the mass in the universe is in the form of non-luminous, nonbaryonic, cold dark matter―whose existence can, so far, only be determined by its gravitational effect on visible mass [1] . In particular, the orbital velocity of objects in galaxies cannot be explained by visible baryonic mass alone.

For galaxies such as the Milky Way, typically ten times more dark matter than visible matter must be assumed [2] in order to explain galaxy rotation curves (plots of the orbital rotation velocity of objects vs. radius of their orbit). Additionally, these rotation curves, which show that rotation velocity is approximately constant as far from the galactic centre as it can be measured, demand a particular distribution of dark matter [3] . By examining galaxy rotation curves, researchers have hypothesized that dark matter is distributed in some kind of oblate shape (usually approximated as spherical) around the galactic center. Overall galactic mass increases approximately linearly with radius as will be derived below. From these galaxy rotation curves the assumption has been made that cold dark matter is found throughout galaxies including in the immediate neighbourhood of stars and, in particular, for our Galaxy, in the neighborhood of the Sun. However, this last assumption, that dark matter is found near stars, is perhaps not correct.

2. Experimental Observations

For our own expanded solar neighbourhood, Garbari and colleagues [4] , using the kinematics of K dwarfs (i.e., K-type main-sequence star), have found the expected, if not slightly more than the expected, dark matter within several hundred parsecs of the Sun. Zhang and colleagues [5] found a similar result within 1.5 kiloparsecs of the Sun. For a complete review on the subject see [6] . A more recent result [7] , based on observations of G & K type main-sequence stars, continues to be in general agreement with the above referenced papers.

However, here on Earth, in the immediate vicinity of the Sun, several experiments designed to directly detect dark matter particles have so far been unsuccessful in finding any dark matter; for example, see Archambault and colleagues [8] , Aprile and colleagues [9] and Aalseth and colleagues [10] . Angloher and colleagues [11] detected events in the acceptance region where a cold dark matter particle signal in the form of low energy nuclear recoils would be expected; but have so far failed to prove these events are due to dark matter. For a summary of the current status of direct dark matter searches see [12] .

3. Hypothesis

Visible and dark matter in a galaxy must, on average, be distributed in the required density to support the galaxy rotation curve. In a region containing only dark matter, dark matter is distributed throughout the region with the required density distribution.

If dark matter only interacts with itself and visible matter gravitationally, then the matter distribution in the region of the galaxy where dark matter is dominant (i.e., away from the galactic center) has to be achieved only through gravitational interaction and the dynamics of the galaxy. If this region of the galaxy also contains concentrated visible matter of higher density than the overall average density in its vicinity (e.g., as the region in the immediate vicinity of the solar system), the overall average matter density necessitated by the observed galaxy rotation curve can only be maintained if dark matter is displaced away from the visible matter.

There are two reasons why the statement is reasonable. First, at every radius the enclosed visible and dark matter must, on average, produce a smooth galaxy rotation curve; if the visible and dark matter cluster, rather than disperse away from each other, then it’s unlikely that we would observe the universal result of relatively constant and smooth rotation curves [2] . Second, N-body simulations [13] and, in particular, three-body [14] simulations have shown that orbiting bodies don’t cluster and actually follow a variety of orbits, that over time and on average, are well distributed in space.

The hypothesis of this paper is: away from the galactic center (where dark matter is dominant), wherever there is concentrated visible matter, dark matter is displaced away from the region around the visible matter―in order to maintain the overall matter density required to achieve the galaxy rotation curve. The size of this region containing no dark matter depends on the average density of matter within that neighbourhood of the galaxy vs. the visible matter in this same region, as will be derived below.

4. Theoretical Development

To explore the extent to which visible matter from a star would affect dark matter distribution in the vicinity of that star, assumptions that are not strictly valid are made in the following analysis. These assumptions, of spherical matter distribution throughout the galaxy and circular orbits, make the initial exploration of the problem theoretically tractable.

At any particular radius r in a galaxy the forces of circular orbits balance [15] , and

, (1)

where V is the rotational velocity of the matter in the orbit of radius r around the galactic center, M_e is the mass enclosed by the orbit and G is the gravitational constant. For a typical high surface brightness galaxy V is approximately constant at most radii [2] [16] ; and, in particular for the Milky Way, in the portion of the Galaxy where our Sun is located. Thus, given that

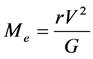, (2)

the density ρ of matter at that radius is 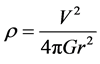[3]

. (3)

Imagine a region (very small―like that of the solar neighborhood) within the Galaxy consisting of only dark matter. This region will have an approximately constant density of nonbaryonic cold dark matter given by Equation (3) evaluated at the particular galactic radius of the region. Now, imagine that we introduce our solar system into this region. In order to maintain equilibrium within the Galaxy, per this paper’s hypothesis, the matter density before and after the solar system is introduced must be the same (given that the solar system mass is inconsequential compared to the Galaxy mass).

The mass contained in the region prior to the introduction of the solar system, consisting of dark matter is: the density in Equation (3) times the volume of the region, given that the dark matter density variation over the extent of the region is inconsequential. After the solar system is introduced the mass in the region is the mass of the solar system plus the new density ρ_n of dark matter times the volume.

We are interested in the region where ρ_n is approximately zero, i.e., where the mass density of the local area is attributed primarily to the solar system visible mass. This occurs for a region of volume v_s such that

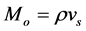, (4)

where M_o is the solar system mass (approximately the solar mass) and where

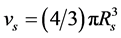. (5)

By combining Equations (3), (4) and (5) we obtain an expression for the radius R_s of the spherical volume v_s in the vicinity of the solar system with approximately zero dark matter density

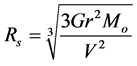. (6)

Inserting the values for our Galaxy and solar system, found in Table 1 [17] [18] , into Equation (6) we obtain R_s ~ 5.3 × 10¹³ km (~1.7 parsecs). This result is about twice the radial extent of the solar system (approximated as the distance to the nearest star or well past the outer edge of the Oort cloud).

In summary, introducing a solar system into a galactic region occupied by dark matter displaces dark matter out of a region of approximately the same radial extent than that occupied by the solar system; in order that the same average galactic mass density be maintained.

5. Conclusions

It is argued herein that nonbaryonic cold dark matter density is dependent upon the distribution of visible matter in its vicinity (up to a few parsecs away in the case of the Sun). Thus, the dark matter density in the expanded solar neighbourhood (a region extending to approximately a kiloparsec and having a radial extent 100 to 500 times larger than the radial extent of the region over which dark matter is displaced) should be unaffected as verified by direct observation of the kinematics of K dwarfs. However, on Earth, in the immediate vicinity of the Sun, we should be expecting a much lower flux of dark matter particles, if any, than that assumed in ongoing direct detection experiments.

The arguments in this paper are based on assumptions that are not strictly valid, but are approximations to allow for the initial theoretical exploration of the problem. It remains to be seen whether or not a proper computer simulation will verify the result that, away from the galactic center, cold dark matter density is dependent upon the distribution of visible matter in its vicinity.

Cite this paper

Daniel E. Friedmann, (2016) Dark Matter Distribution in the Vicinity of Stars. Open Access Library Journal,03,1-4. doi: 10.4236/oalib.1102421

References