Open Access Library Journal
Vol.02 No.12(2015), Article ID:69017,11 pages
10.4236/oalib.1102033
Optimal Portfolios of an Insurer and a Reinsurer under Proportional Reinsurance and Power Utility Preference
Silas A. Ihedioha1, Bright O. Osu2
1Government Day Secondary School Bwari Federal Capital Territory, Abuja, Nigeria
2Department of Mathematics, Michael Okpara University of Agriculture Umudike, Umuahia, Nigeria
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 December 2015; accepted 25 December 2015; published 29 December 2015
ABSTRACT
This study tackled portfolio selection problem for an insurer as well as a reinsurer aiming at maximizing the probability of survival of the Insurer and the Reinsurer, to assess the impact of proportional reinsurance on the survival of insurance companies as well as to determine the condition that would warrant reinsurance according to the optimal reinsurance proportion chosen by the insurer. It was assumed the insurer’s and the reinsurer’s surplus processes were approximated by Brownian motion with drift and the insurer could purchase proportional reinsurance from the reinsurer and their risk reserves followed Brownian motion with drift. Obtained were Hamilton-Jacobi-Bellman (HJB) equations which solutions gave the optimized values of the insurer’s and the reinsurer’s optimal investments in the risky asset and the value of the discount rate that would warrant reinsurance as a ratio of their portfolio weights in the risky asset.
Keywords:
Proportional Reinsurance, Optimal Investment, Insurer, Reinsurer, Hamilton-Jacobi-Bellman (HJB) Equation, Power Utility Function
Subject Areas: Financial Mathematics

1. Introduction
The first study on optimal reinsurance was done by Bruno de Finetti as pointed out by Centeno and Simões [1] . In his study, de Finetti analyses the optimal retention limit for quota-share proportion reinsurance policies, under one year period and infinite time horizon using mean-variance criteria. There have been several studies thereafter, on the effect of reinsurance on the ultimate probability of ruin (Gerber [2] ; Waters [3] ; Bowers et al., [4] , Centeno, [5] ; Hesselager, [6] ). Most of these earlier studies concentrated on the effect of reinsurance on the adjustment coefficient [1] .
Schimidli [7] considered the risk process modelled by Cramer-Lundberg model and found the optimal unlimited proportional reinsurance strategy that minimized the infinite time ruin probability. He proved the existence of a smooth solution of the corresponding Hamilton-Jacobi-Bellman equation as well as verification theorem. Some numerical examples with exponential, shifted exponential and Pareto claims were carried out. The corresponding problem has been also studied by Hipp and Vogt [8] for the case of dynamic XL reinsurance.
[7] considered a classical risk model and allowed investment into a risky asset modelled as a Black-Scholes model as well as (proportional) reinsurance in the Cramer-Lundberg set up and solved the problem on determination of optimal reinsurance and investment strategies that minimized probability of ruin using the Hamilton- Jacobi-Bellman approach. He found optimal levels of investment and reinsurance that minimized the ruin probability of only investment in risk asset.
Taksar and Markussen [9] extended the analysis of this study by proposing a diffusion model with investment and proportional reinsurance.
Hipp and Plum [10] considered a risk process modelled as a compound Poisson process. They seek to minimize the ruin probability of the risk process by choosing suitable investment strategies for the market index (risky asset). They computed the optimal strategy using the Bellman equation and proved the existence of a smooth solution and a verification theorem, and give explicit solution in some cases with exponential claim size distribution, as well as numerical results in a case with Pareto claim size. This problem had been also studied by Browne [11] for the case then the insurance business is modelled by Brownian motion with drift, and the risky assert is modelled by geometric Brownian motion.
Liu and Yang [12] extended the model studied by [10] by including risk-free asset. They assumed that the insurance company receives premiums at constant rate and that it can invest in the money market and in a risky asset. They investigated behavior of various claim-size distributions numerically and computed the optimal investment strategy and the solution of the associated HJB equation under each assumed claim-size distribution. They also consider the effect of changes in various factors, like stock volatility, on the optimal investment strategies and survival probability.
Castillo and Parrocha [13] considered an insurance company with the fixed amount available for investment in a portfolio consisting of one risky assert and one risk-free asset and gave a numerical algorithm for solving the resulting HJB equation.
Irgens and Paulsen [14] considered the problem of maximizing the expected utility of the assets of an insurance company at a terminal time by reinsurance and investments into a diffusion-perturbed classical risk process. In their study they assumed that the company is allowed to invest its surplus in either a risk-free asset or a risky one.
Paulsen et al. [15] considered the diffusion perturbed classical risk process compounded by a linear Brownian motion and allowed for stochastic return on investments and presented sufficient conditions for the survival probability function to be four times continuously differentiable, which in particular implies that the survival probability is the solution to a second order integro-differential equation. Transforming this equation into an ordinary Volterra-integral equation of the second kind, they analyzed properties of its numerical solution by applying the order-four block-by-block method in conjunction with Simpson’s rule. Their study only allows investments and does not incorporate any type of reinsurance.
Paulsen [16] studied the ruin models with investment income. This survey treats the problem of ruin in a risk model when assets earn investments. In addition to a general presentation of the problem, the study also presented the relevant integro-differential equations, exact and numerical solutions, asymptotic results, ruin probabilities in the presence of investments and possibly reinsurance. In particular, the study considered the case where the insurer has possibility of purchasing a proportional reinsurance contract as well as investing in both risk-free and risky asset with the purpose of minimizing probability of ruin. The main emphasis was on continuous time models, though discrete time models were also covered.
Meng and Zhang [17] considered an insurance company whose surplus is modelled by Brownian motion with drift and that the surplus can be invested in a risky or nonrisk asset with the objective of minimizing the probability of ruin of insurer. They formally established that XL reinsurance treaty is optimal among the class of plausible reinsurance treaties. They also obtained optimal retention level as well as providing an explicit expression of the minimal probability of ruin.
Kasumo [18] considered a diffusion-perturbed risk process incorporated with proportion reinsurance and investment process of Black-Scholes type. The main purpose was to determine the role of investment and proportional reinsurance on the minimization of probability of ultimate ruin of an insurance company. The HJB equation for this problem was derived and the corresponding Volterra-integral differential equation which was then transformed into a linear Volterra integral equation of the second kind. He solved the integral equation using block-by-block numerical method for the retention percent that minimizes the probability of ultimate ruin.
Mata [19] studied the excess of loss reinsurance and reinstatement problem and provide a methodology to calculate the distribution of the aggregate losses for two or more consecutive Layers when there are a limited number of reinstatements.
In this study we consider the risk reserve of an insurer and a reinsurer to follow Brownian motion with drift and tackled their portfolio optimization problem. The optimized values of the insurer and the reinsurer are calculated. Also calculated are the insurer’s and the reinsurer’s optimal investment in the risky asset and then the discount value, 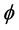 , that would warrant reinsurance.
, that would warrant reinsurance.
To make for clear understanding of this work, we defined the following few terms;
Insurance: Insurance is an arrangement by which a company gives customers financial protection against loss or harm such as theft or illness in return for a payment called a premium (Encarta World English Dictionary [20] ).
Reinsurance: This is the transfer of risk from a direct insurer (the cedent) to a second insurance carrier (the reinsurer). It may also be defined as insurance for insurers. It serves the purpose of offering protection to cedents against very large individual claims or fluctuations in their aggregate portfolio of risks, as well as diversifying the financial losses caused by it [1] .
Risk: This is the probability of loss to an insurer or the amount that an insurer is in danger of losing [20] .
Optimal portfolio: An optimal portfolio is a portfolio in which the risk-reward combination is such that it yields the maximumreturns (provides the highest utility) possible under the current and anticipated circumstances. Its mathematical formulation was provided the University of California's noble laureate economist Harry Markowitz (born 1927) in 1952.
Portfolio reinsurance: The practice whereby an insurer transferssome or all of the risk attached to a portfolio to another insurer, or reinsurer. Insurers use portfolio reinsurance to reducethe risk of having to pay large claims in the event of significant losses to the value of the portfolio.
2. Model Formulation and the Model
Suppose the claim process 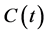 of an insurance company is described by;
of an insurance company is described by;
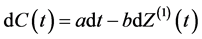 , (1)
, (1)
where a and b are positive constant and 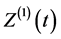 a standard Brownian motion defined on a complete probability space
a standard Brownian motion defined on a complete probability space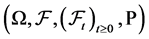 .Assuming also that the premium rate is;
.Assuming also that the premium rate is;
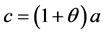 (2)
(2)
with safety loading (security risk premium)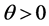 .
.
Using equation (1), the surplus process of the insurer is given by;
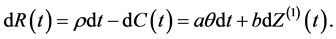 (3)
(3)
The insurance company has the permission to purchase proportional reinsurance to reduce her risk and pays reinsurance premium continuously at the rate of 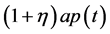 where
where 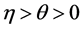 is safety loading of the reinsurer and
is safety loading of the reinsurer and 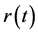 is the proportion reinsured at time t.
is the proportion reinsured at time t.
The surplus of the insurance company is then given as;
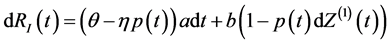 , (4)
, (4)
for the insurer, and
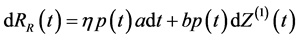 , (5)
, (5)
for the reinsurer, (Danping et al. [21] ).
Assuming that the insurer and reinsurer invest their surplus in the same market consisting of two assets: a risky asset (stock) and a riskless asset (bond) which rate of return is a linear function of time, let the prices the riskless and be risky assets 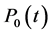 and
and 

and

(Osu and Ihedioha, [22] [23] ), respectively.





Both the insurer and there insurer hold the risky asset as long as.

Let 





and for the reinsurer the strategy 



Assume that 



For the corresponding admissible strategies,



for the insurer, and

for the reinsurer (Wokiyi, [24] ).
Substituting the expressions for, 




for the insurer and;

for the insurer.
The quadratic variations of the wealth processes of the insurer and the reinsurer are;


Suppose the investor has a power utility function, the Arrow-Pratt measure of relative risk aversion (RRA) or coefficient of relative risk aversion is defined as;

where w is the wealth level of an investor. The special case being considered is where the utility function is of the form,

which has a constant relative risk aversion parameter

where

and 
Subject to:
for the insurer and;
for the reinsurer.
3. The Optimization
3.1. The Case of the Insurer
The theorem that follows gives the optimization of the insurer’s wealth;
Theorem 1: The optimal policy that maximizes the expected power utility at terminal time T is to invest at each time

with optimal proportion reinsured,

and value function;

where 

Proof:
We derive the Hamilton-Jacobi-Bellman (HJB) partial differential equation starting with the Bellman equation:

where 

Rewriting Equation (25) as,

and dividing both sides of the equation by 


Ito’s lemma (Miao, [25] ), which states that;

For the insurer, substituting in the Ito’s lemma for 


Equation (28) simplifies to;

Applying (29) to the Bellman Equation (26) and taking expectation, we get the HJB equation;

where,

satisfying terminal condition,

Observing the homogeneity of the objective function, the restriction and the terminal condition, we conjecture that the value function V must be linear to
Let

be such a value function, such that at the terminal date, T

then

Substituting Equation (35) into Equation (30), we obtain; the new H-J-B equation,

To obtain the optimal value 



This simplifies to;

This is the insurance company’s optimal investments in the risky asset, stock, that is both horizon and wealth dependent.
Also, differentiating Equation (36) with respect to 

This reduces to;

The solution of the HJB Equation (36) is thus; replacing 




From which we obtain,

Since t is the dominating variable, as implied in our choice of

where

The integral of the differential equation of the function g is obtained as;

where 

That is;

Applying the terminal condition, 

This implies that the horizon dependent solution to the insurance company’s investment problem is:

This is the maximized expected power utility value at time t under optimal investment policy.
3.2. The Case of the Reinsurer
For the reinsurer, we state the following theorem 2.
Theorem 2: The optimal policy to maximize the expected power utility at T is to invest at each time

with optimal proportion reinsured,

and value function;

where 
Proof:
Adopting Equations (25) to (35) and replacing






which reduces to;

To obtain the optimal investment in the risky asset, Equation (53) is differentiated with respect to

Solving for 

The differentiation of (53) with respect to 

From equation (55) which when reduced gives;

where,

the definite integration within 

Applying the terminal condition, 

This implies that the horizon dependent solution to the insurance company’s investment problem is:

3.3. The Equality of the Insurer’s and the Reinsurer’s Strategies
Here we find the condition under which the proportion reinsured by the Insurer equals the amount accepted to be insured by the Reinsurer.
Therefore, we equate the values of 

That is;

This reduces to;

where;

Therefore,

where, wr and wi are the Reinsurer’s and the Insurer’s portfolio weights in the risky asset, respectively.
Clearly, the optimal policies that maximize the expected power utility and the value functions for both the insurer and the Reinsurer are horizon dependent.
4. Conclusions
In this study, we consider the optimal investment problem for both an insurer and a reinsurer. The basic claim process is assumed to follow a Brownian motion with drift and the Insurer could purchase proportional reinsurance from the Reinsurer.
The Reinsurer and the Insurer were allowed to invest in a risky and a risk-free assets and expressions for their optimal portfolios obtained solving the corresponding HJB equations. The discount value, 
Cite this paper
Silas A. Ihedioha,Bright O. Osu, (2015) Optimal Portfolios of an Insurer and a Reinsurer under Proportional Reinsurance and Power Utility Preference. Open Access Library Journal,02,1-11. doi: 10.4236/oalib.1102033
References
- 1. Centeno, M.L. and Simoes, O. (2009) Optimal Reinsurance. Real Academia de Ciencias Serie A. Matematica, Espana, 2, 387-405.
- 2. Gerber, H.U. (1979) An Introduction to Mathematical Risk Theory. S S Huebner Foundation Monographs, University of Pensylvama Waters H, 1979, Excess of Loss Reinsurance Limits, 37-43.
- 3. Bowers, N.L., Gerber, H.U., Hickman, J.C., Jones, D.A. and Nesbitt, C.J. (1987) Actuarial Mathematics. Society of Actuaries, Chicago.
- 4. Centeno, M.L (1986) Measuring the Effect of Reinsurance by the Adjustment Coefficient. Insurance: Mathematics and Economics, 5, 169-182.
http://dx.doi.org/10.1016/0167-6687(86)90043-0 - 5. Hesselager O, 1990, Some results on Optimal Reinsurance in terms of the Adjustment Coefficient. Scandnavian Actuarial Journal.80-95.
- 6. Schmidli, H. (2000) Optimal Proportional Reinsurance Policies in a Dynamic Setting. Research Report 403, Arhus University, Arhus.
- 7. Hipp, C. and Vogt, M. (2003) Optimal Dynamical XL Reinsurance. ASTIN Bulletin, 33, 193-207.
http://dx.doi.org/10.2143/AST.33.2.503690 - 8. Schmidli, H. (2002) On Minimizing the Ruin Probability by Investment and Reinsurance. Annals of Applied Probability, 12, 890-907.
http://dx.doi.org/10.1214/aoap/1031863173 - 9. Taksar, M.I. and Markussen, C. (2003) Optimal Dynamic Reinsurance Policies for Large Insurance Portfolios. Finance and Stochastics, 7, 97-121.
http://dx.doi.org/10.1007/s007800200073 - 10. Hipp, C. and Plum, M. (2000) Optimal Investment for Insurers. Insurance: Mathematics and Economics, 27, 215-228.
http://dx.doi.org/10.1016/S0167-6687(00)00049-4 - 11. Browne, S. (1995) Optimal Investment Policies for a Firm with a Random Risk Process: Exponential Utility and Minimizing the Probability of Ruin. Mathematics of Operations Research, 20, 937-958.
http://dx.doi.org/10.1287/moor.20.4.937 - 12. Liu, C.S. and Yang, H. (2004) Optimal Investment for an Insurer to Minimize Its Probability of Ruin. North American Actuarial Journal, 2, 11-31.
http://dx.doi.org/10.1080/10920277.2004.10596134 - 13. Castillo, M.T. and Parrocha, G. (2003) Stochastic Control Theory for Optimal Investment. Working Paper, Department of Actuarial Studies, University of New South Wales, Sydney.
- 14. Irgens, C. and Paulsen, J. (2004) Optimal Control of Risk Exposure, Reinsurance and Investments for Insurance Portfolios. Insurance, Mathematics and Economics, 35, 21-51.
http://dx.doi.org/10.1016/j.insmatheco.2004.04.004 - 15. Paulsen, J., Kasozi, J. and Steigen, A. (2005) A Numerical Method to Find the Probability of Ultimate Ruin in the Classical Risk Model with Stochastic Return on Investments.
- 16. Paulsen, J. (2008) Ruin Models with Investment Income. Probability Surveys, 5, 416-434.
http://dx.doi.org/10.1214/08-PS134 - 17. Meng, H. and Zhang, X. (2010) Optimal Risk Control for the Excess-of-Loss Reinsurancepolicies. Astin Bulletin, 40, 179-197.
http://dx.doi.org/10.2143/AST.40.1.2049224 - 18. Kasumo, C. (2011) Minimizing Probability of Ultimate Ruin by Proportiona Reinsurance and Investment. Msc Dissertation, University of Dar es salaam, Dar es salaam.
- 19. Mata, J.A. (2000) Pricing Excess of Loss Reinsurance with Reinstatement. Astin Bulletin, 30, 349-368.
http://dx.doi.org/10.2143/AST.30.2.504640 - 20. Encarta World Dictionary, 1999.
- 21. Danping, L.I. (2015) Optimal Investment Problem for an Insurer and a Reinsurer under the Proportional Reinsurance. WSEAS Transactions on Mathematics, 14, 20-35.
- 22. Osu, B.O. and Ihedioha, S.A. (2012) Optimal Portfolio Selection for Pension Funds with Variable Rate of Return and Transaction Costs: Finite Horizon Case. Global Journal of Pure and Applied Mathematics, 8, 275-286.
- 23. Osu, B.O., Ihedioha, S.A. and Adindu-Dick, J.I. (2014) On the Survival of Insurance Company’s Investment with Consumption under Power and Exponential Utility Functions. American Journal of Applied Mathematics, 2, 8-13.
http://dx.doi.org/10.11648/j.ajam.20140201.12 - 24. Wokiyi, D. (2012) Maximizing Investment Returns of an Insurance Company While Minimizing the Probability of Ruin. Master’s Thesis, University of Dares-Salam, Dar es salaam, 1-60.
- 25. Nie, M. (2010) Optimal Investment Policy for Pension Funds with Transaction Costs: The Finite Horizon. Master’s Thesis, Center Graduate School, Finance, Tilburg, 1-49.







