Open Access Library Journal
Vol.02 No.12(2015), Article ID:69009,7 pages
10.4236/oalib.1101475
Open Channel Flow over a Permeable River Bed
Godwin Christopher Ezike Mbah, Cyril Ifeany Udogu
Department of Mathematics, University of Nigeria, Nsukka, Nigeria

Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 December 2015; accepted 20 December 2015; published 24 December 2015
ABSTRACT
This paper presents results of a modeled open channel flow through a porous media (River). In the model, we considered water as an incompressible fluid; the flow as steady and uniform; the system is assumed to be isothermal and the flow pattern is laminar. We have solved the resulting Brinkman equation using analytical method. By some mathematical operation, the momentum partial differential equation (PDE) was reduced to ordinary differential equation (ODE) and the resulting equations are solved analytically using the standard solution technique for a second order ODE. The analysis of the result was done and plotted on graph using MATLAB to show the effect of permeability on flow parameters such as velocity, pressure gradient and height of the channel. It is found that velocity of the open channel decreases with increase in permeability. Also, increase in the height of the open channel results in increase in velocity of flow in the open channel. We also found that an increase in the permeability of an open channel resulted in decrease in pressure.
Keywords:
Fluid, Flow, Permeable River Bed, Open Channel
Subject Areas: Fluid Mechanics

1. Introduction
As a result of the importance of open channel flow, and the occurrence of porous media in a wide variety of important practical applications, the overall objective of this work is to provide analytical technique for treating problems which involve flow of an open channel through porous media. Specifically flow through a permeable river bed.
The flow of water in an open channel is a familiar sight, whether in a natural channel like that of a river [1] or an artificial channel like that of an irrigation ditch. Its movement posses a difficult problem when everything is considered especially with the variability of natural channels. However in many cases the major features are expressed in terms of only few variables, whose behavior can be described adequately by a simple theory.
The principal forces at work during fluid flow are those of inertia, gravity, viscosity and pressure gradient [2] - [4] .
In this study, water is considered as the fluid with a known density of 1 g/cc and does not vary significantly for the temperature and pressure that would be considered in this paper.
The total volume of water transported downstream by a river has been observed. From [1] we see a combination of the free water flow together with a substantial contribution to flow through subsurface rocks and gravels that underlie the river and its flood plain. It has also been observed that some rivers flow intermittently. They only flow occasionally and can be dry for several years at a time. This has been attributed to geological conditions such as highly permeable river bed [1] and [5] .
Although almost all natural channels have permeable beds such as gravel Bed Rivers, not much research has been undertaken in order to study the effect of channel bed permeability on the mean and instantaneous flow. In common practice a permeable bed has usually been treated analogously to an impermeable bed and flow resistance coefficient and velocity distributions derived irrespectively of bed porosity. From [6] it was observed that depending on the permeability of the subsurface, significant interaction processes occur between the flow above the porous bed and the subsurface area. The effects of this interaction are a non-zero velocity at the permeable boundary. They also observed that the driving force which is responsible for the exchange processes between the pore layer and the upper flow is the presence of local pressure gradients.
According to [7] and [8] , fluid flow in a porous media shows some of the characteristics of flow in the absence of rigid matrix and in such a flow regime, the inertia and fluid shear stress effects not included in the Darcy model become significant affecting the flow characteristics. Flow in solid media or flow in the absence of a rigid matrix is governed by some fundamental laws based on the conservation of mass, momentum and energy.
It has become pertinent to study open channel flow over a permeable river bed so that in managing or controlling a river to make it more useful or less disruptive to human activity, the effect of permeability would be considered.
When some rivers dry up as a result of permeability this will result to drop in energy supply, affect habitat conservation and some other uses of the river. The permeability of a river may contribute to the over flow of its bank and consequently lead to over flooding.
2. Methodology
The equation governing flow in a porous media with impermeable walls on the sides are given by:
Mass Conservation

The continuity equation:
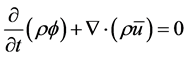 For compressible fluid (1)
For compressible fluid (1)
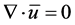 For incompressible fluid (2)
For incompressible fluid (2)
The momentum Equation:
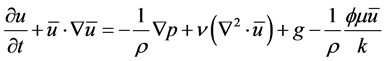 (3)
(3)
This takes care of inertia and fluid shear stress effects which are not included in the Darcy model for a porous media. In the above equations 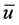 is intrinsic velocity vector,
is intrinsic velocity vector, 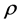 is density of fluid, p is pressure,
is density of fluid, p is pressure, 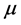 is viscosity of fluid, k is the permeability of the channel and
is viscosity of fluid, k is the permeability of the channel and 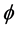 is the volume fraction of fluid within the porous region (porosity). In this study,
is the volume fraction of fluid within the porous region (porosity). In this study, 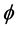 is taken to be constant through the porous media.
is taken to be constant through the porous media.
Based on reports from [9] - [12] , if we assume the following:
Incompressible/homogeneous flow;
Steady/uniform channel flow;
Hydro-static pressure
Isothermal system
Density of water is 1 g/cc and
Two dimensional flow
Equation (3) simplifies to:
X-component
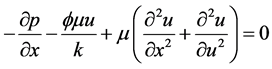 Brinkman Equation (4)
Brinkman Equation (4)
Y-Component
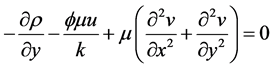 Brinkman Equation (5)
Brinkman Equation (5)
3. Analytic Solution
Flow is in the x-direction. Hence the equation
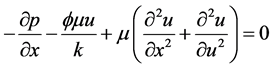
is considered.
The velocity profile is the same at all distances down the channel; that is at all x. Therefore it is a function of y only. Thus
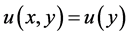
The viscous force is along the y-axis
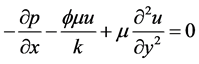 (6)
(6)
In fully developed region, pressure drop in porous media and open channel are equal as follows:

Hence Equation (6) involves only one independent variable y.

Or

where G is pressure drop,
Modeling fluid flow in open porous channel presents difficulty to solve the governing equations of open channel and porous media simultaneously. The one possible approach to handle this is to divide the medium into two regions.
The porous region and (2) The open region.
Solve the equations of the two regions separately and then apply the boundary conditions, [7] . Hence, we have;


4. Boundary Conditions
For the boundary conditions, [13] , we have:
At the inlet face, a uniform velocity is specified

At the outlet, velocity is extrapolated to the exit plane

At the sides with impermeable walls no slip condition is enforced

At a section in which the flow is fully developed along the duct, the shear stress equality is enforced as


Equation (9) is solved analytically [14] - [17] using the standard solution technique for a constant coefficient second order ODE and the following solution is reached at:

where
From Darcy’s law

and

Substituting Equation (18) into Equation (10) and solving the resulting equation, we have




5. Results and Discussions
Figure 1 shows the effects of permeability on the velocity of flow in an open channel over a permeable river bed. Velocity 





It can be seen that velocity decreases with increase in permeability. When the porous media is highly permeable, the behavior of the porous media does not differ too much from the open channel. However, when permeability is low the deviation of velocity of the porous media from the open channel is clear.
Figure 2 shows the effect of velocity on the depth of the river. Velocity (

This is also an indication that as the depth of the river increases, the effect of permeability also decreases though not in the same proportion as velocity.
Figure 3 shows the effect of permeability on pressure drop or pressure gradient. The data used in Figure 3 were generated from the solution.
Figure 1. Graph of velocity against permeability.
Figure 2. Graph of pressure gradient against permeability.
Figure 3. Graph of velocity against the height of fluid in the channel.
Y is kept constant at 1 cm, while k is varied. It is observed that pressure gradient (G) decreases with increase in permeability. When pressure gradient decreases, there is a decrease in the resistance against the flow in the porous media, which causes a penetration from the open channel to the porous media or we say the penetration is from the flow above the porous bed to the subsurface area. Hence high permeability accounts for some rivers drying up intermittently. In the other hand, when permeability is low, pressure gradient is high and resistance to flow in the vertical direction is high. Hence there is a penetration from the subsurface area to the flow above the porous media. This adjusts the mass flow in open channel and porous media in order to have identical pressure drop in x-direction. This again accounts for the early statement that the total volume of water transported downstream by a river, is a combination of the free water flow together with a substantial contribution to flow through subsurface rock gravels that underlie the river and its flood plain.
6. Conclusions
Open channel flow over a permeable riverbed is studied by obtaining analytical solution for the fully developed region. Equation (16) gives solution for open channel flow over a permeable riverbed, while Equation (19) gives solution for pressure drop in an open channel flow.
It is observed that by decreasing the permeability in Darcy, due to increase in resistance against the flow in the porous region, the difference between the maximum of velocity profile in porous region and open channel increases. This is as was predicted physically. It is also shown that there is a penetration of flow from porous media to open channel due to resistance against flow in the porous media and this penetration increases by decreasing the permeability. This penetration adjusts the mass flow in open and porous regions in order to have identical pressure difference in x-direction for both the open channel and the porous media. In the other hand, when permeability is high, there is a penetration from the open channel to porous media due to decrease in resistance against flow. Hence high permeability accounts for rivers meandering up and down. This becomes obvious in desert areas, where the river beds are sandy and drought is a problem. As the level of a desert stream drops, places where it was at the bottom of its “wave” dry up, and all you can see is sand in the riverbed. But if you walk downstream away, you will come to where it was at the top of its “wave” and you can still see water in that section.
Water is flowing in both places, although where one saw it as dry, it is still flowing but only underground.
7. Recommendation
When the permeability of a river is high, flooding in that area will not be catastrophic. Rainfall and snow melt will cause temporary and gradual flooding. By creating “hard” or impermeable surfaces like roads, parking lots, sidewalks, patios and roofs, water will be collected in channels that will cause water flow. This is called urban runoff. Instead of soaking into the ground and recharging the aquifer, rainfall begins to collect and then simply flow over these hard surfaces, running directly into streams. The result is that aquifer levels go down, lowering the level of the streams, while runoff during rainfall increases, creating sudden and unseasonal flooding.
Wet lands like swamps and marshes should not be filled with dirt. Without wetlands, rainwater enters the river directly and causes catastrophic flooding.
Dams or weirs may be built to control the flow, store water or extract energy. The management of river is a continuous activity as rivers tend to “undo” the modifications made by man.
Cite this paper
Godwin Christopher Ezike Mbah,Cyril Ifeany Udogu, (2015) Open Channel Flow over a Permeable River Bed. Open Access Library Journal,02,1-7. doi: 10.4236/oalib.1101475
References
- 1. How a River Flows. (From Wikipedia, the Free Encyclopaedia. Accessed 24th September, 2002)
http://chamisa.freeshell.org//flow.htm - 2. Batchelor, G.K. (1967) An Introduction to Fluid Dynamics. Cambridge University Press, New York, 223-224.
- 3. Tritton, D.J. (1977) Physical Fluid Dynamics. Van Nostrand Reinhold (UK), 3-12.
http://dx.doi.org/10.1007/978-94-009-9992-3 - 4. Calvert, J.B. (2003) Open Channel Flow.
http://mysite.du..edu/-etuttle/tech/opench.htm - 5. River. (From Wikipedia, the Free Encyclopaedia. Accessed 1st March 2012)
http://enWikipedia.org/wiki/river - 6. Stoesser, T., Frohlich, J. and Rodi, W. (2007) Turbulent Open Channel Flow over a Permeable Bed. Proceedings of 32nd IAHR Congress, Venice, 1-6 July 2007, 10p.
- 7. Radiom, M., Khakbaz, M. and Kermani, M.J. (2007) Numerical and Analytical Calculation of Air flow through an Open Channel Linked to a Porous Media. Department of Mechanical Engineering, Amirkabir University of Technology (Tehran Polytechnic), Tehran, 15875-4413.
- 8. Nabovati, A. and Sousa, A.C.M. (2007) Fluid Flow Simulation in Random Porous Media at Pore Level Using the Lattice Boltzmann Method. Journal of Engineering Science and Technology, 2, 226-237.
- 9. Parvazinia, M., Nassehi, V. and Wakeman, R.J. (2006) Multiscale Finite Element Modelling of Laminar Steady Flow through Highly Permeable Media. Chemical Engineering Science, 61, 583-596.
http://dx.doi.org/10.1016/j.ces.2005.07.018 - 10. Zagni, A.F.E. and Smith, K.V.H. (1976) Channel Flow over Permeable Beds of Graded Spheres. Journal of the Hydraulics Division, 102, 207-222.
- 11. Aaltosalmi, U. (2005) Fluid Flow in Porous Media with the Lattice-Boltzmann Method. Academic Dissertation for PhD, University of Jyväskylä, Jyväskylä, 5-8.
- 12. Heinemann, Z.E. (2005) Fluid Flow in Porous Media. Petroleum Engineering Science, 1, 6-12.
- 13. Zippe H.J Graf. W.H. (1983) Turbulent Boundary Layer Flow over Permeable and Non-Permeable Rough Surfaces. Journal of Hydraulic Research, 21, 51-65.
http://dx.doi.org/10.1080/00221688309499450 - 14. Obikwelu, D.O.N. (2003) Differential Equations and Application. AMDI-Nel Publishers Ogidi, Nigeria, 60-61.
- 15. Wang, J., Gao, Z., Gan, G. and Wu, D. (2001) Analytical Solution of Flow Coefficients for a Uniformly Distributed Porous Channel. Chemical Engineering Journal, 84, 1-66.
http://dx.doi.org/10.1016/S1385-8947(00)00263-1 - 16. Spiege, M.R. (1983) Advanced Mathematics for Engineers and Scientists. McGraw-Hill Book Company, Singapore, 74-83.
- 17. Rajput, R.K. (1998) Fluid Mechanics and Hydraulic Machines. Schand and Company, Ram Nagar, New Dehi, 3-29, 867-871.






