Received 28 November 2015; accepted 13 December 2015; published 18 December 2015

ABSTRACT

Use of low bend loss optical fibers in fiber-to-the-home (FTTH) networks becomes unavoidable to improve the optical networks performance. One of the candidates is photonic crystal fibers (PCFs) for their low bend loss properties. This paper presents procedures for optimization of the bend loss of PCFs with small and large mode areas by using solvers Softwares Rsoft and Optifiber. The optimizations are performed with respect to bend radius, core radius, photonic crystal pitch and the ratio of air-filling factor. The lowest bend loss of 1 dB/cm was obtained at bend radius of 56 mm and core diameter of 22 micrometer.

Keywords:

Optimization, Macrobending Loss, Photonic Crystal Fibers

Subject Areas: Electric Engineering

1. Introduction

In the past decade, fiber-to-the-home (FTTH) has attracted attention of researchers for its applications in optical networks to meet the ever-increasing demands to improve the networks performance [1] . To implement the FTTH technology, bend insensitive single-mode fibers have become popular for their small bend radii of 5 mm with low bend losses. For a high performance network, the bend loss of less than 0.1 dB/m is required [2] . A good number of methods are suggested to reduce the bending losses of single-mode fibers, which include uses of depressed cladding [3] , low index trench [4] , reduced mode field diameter [5] .

Photonic crystal fibers (PCFs) with their peculiar properties and structures have been the subject of considerable researches for various applications in optical system, specifically in FTTH [6] [7] . The structures of PCFs are more flexible compared to the conventional single-mode fibers when designing for low bend losses fibers [8] - [11] .

In this paper, for determination of PCF cladding index, solver softwares Optifiber and Rsoft are employed. In every step of simulations, by varying the diameter and pitch of the air-holes, the effective index of PCF cladding is calculated at wavelength 1550 nm. In each stage of our calculation, the effective refractive index of the cladding of PCFs is approximated with a step-index single-mode fiber. The macrobending losses of each modeled PCF for different bend radii and core diameters are determined at wavelength 1550 nm. However, while considering different core diameters, the attention was focused on single-mode operation of the modeled PCFs. The optimization of macrobending losses of PCFs was performed for core diameter, bend radius, and air filling factor. It was observed that by increasing air-hole diameter d or increasing the pitch 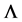of the PCFs with constant ratio of air filling factor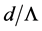, the effective index of the PCFs would accordingly increase. In addition, when the value of 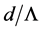increases, the effective index of cladding will reduce.

2. Large Mode Area PCF

A large mode area (LMA) PCF with hexagonal cross-section of six rings of air-holes with triangular lattice in the cladding is illustrated in Figure 1, where 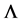denotes the spacing between the air-holes, d represents air- hole diameter, and denotes the air filling factor [11] [12] .

The variation of macrobending loss of the PCF for different core diameters in terms of the bend radius is plotted in Figure 2. We note that the highest core diameter of the LMA-PCF to support single-mode operation is found to be 13 mm. The value of effective cladding index is found to be 1.4473.

By considering two cases of choosing values for the air-hole diameter d and the pitch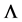, the air-filling factor ratio 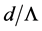varies, and accordingly for each case of varying d (or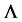) whilst keeping the other constant, the effective index of the cladding is determined for equivalent model of step-index SMF for LMA-PCF. The results of the calculations are tabulated in Table 1.

For different bend radius and air-hole diameters, the macrobending losses are calculated and the corresponding results are illustrated in Figure 3(a) and Figure 3(b) for the core radius 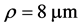and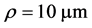, respectively, at wavelength 1550 nm.

We note that for a specified macrobending loss at a given air-hole diameter, when core radius increases, the required bend radius would decrease. In addition, at specified core radius of the PCF, when air-hole diameter increases, the bend radius will decrease. In General, for higher values of the core diameter, almost the same macrobending losses are obtained at lower bending radii.

The investigation on effect of variations of on macrobending losses is plotted in Figure 4 for the core radius of and at a constant air-hole diameter of and wavelength of 1550 nm.

The results in this case indicate that with a constant value of d, when increases, the macrobending loss would also increase. On the comparison with the results in Figure 3, under similar condition, the level of macrobending losses has considerably reduced.

3. Small Mode Area PCF

With a similar structure, as in Figure 1, a PCF with a small mode area (SMA) is considered in the first case with and varying, and in second case with and varying d. By modal analysis of SMA-PCF, the highest core diameter to guarantee single-mode operation is found to be 4.2 mm. With variations of core radius and for a constant and, the macrobending losses are calculated and drawn as a function of bend radius, as shown in Figure 5.

We note that the macrobending loss in SMA-PCF is much less than that of the fiber LMA-PCF. By considering a constant range of macrobending loss, the variation range of the LMA-PCF is about 30 times higher than the SMA-PCF. The calculated effective index for different d and values are tabulated in Table 2.

For SMA-PCFs, the variations of macrobending losses in terms of bend radius for different values of d are plotted in Figure 6. For each case, the value of is kept constant at 2.1 mm, while the air-hole radius was varied from to. By increasing air-hole diameter up to 1.17 mm, macrobending losses, with respect to bend radius, would reduce, but by further increase of d has opposite effect, such that from, the level of macrobending loss would increase, as shown in Figure 6. Further, when the core radius increases, the macrobending loss will decrease.

In addition, the effects of on the macrobending loss is investigated and the results are plotted against bend radius for constant. It worth to note that in this case when the pitch goes to higher levels, the macrobending loss would also increase, simultaneously, as illustrated in Figure 7.

4. Conclusion

This paper presents simulation of two proposed photonic crystal fibers to optimize the macrobending losses at different parametric conditions by using solvers softwares Rsoft and Optifiber. The smallest bend radius for

SMA-PCF with, , and core radius of were obtained at bending radius of At this bend radius, the macrobending loss was less than 1 dB/m. In case of LMA-PCF, for 1 dB/m macrobending loss, the bend radius is 56 mm and the core diameter is found to be 22 mm.

Cite this paper

Faramarz E. Seraji,Samira Kasiri, (2015) Optimization of Macrobending Loss in Small and Large Mode Area Photonic Crystal Fibers. Open Access Library Journal,02,1-6. doi: 10.4236/oalib.1102269

References