Received 26 November 2015; accepted 12 December 2015; published 17 December 2015

ABSTRACT

A new variational method has been proposed for studying the equilibrium states of the interacting particle system to have been statistically described by using the density matrix. This method is used for describing conductivity electrons and their behavior in metals. The electron energy has been expressed by means of the density matrix. The interaction energy of two ε_kk’ electrons dependent on their wave vectors k and k’ has been found. Energy ε_{k k’} has two summands. The first energy I summand depends on the wave vectors to be equal in magnitude and opposite in direction. This summand describes the repulsion between electrons. Another energy I summand describes the attraction between the electrons of equal wave vectors. Thus, the equation of wavevector electron distribution function has been obtained by using the variational method. Particular solutions of the equations have been found. It has been demonstrated that the electron distribution function exhibits some previously unknown features at low temperatures. Repulsion of the wave vectors k and −k electrons results in anisotropy of the distribution function. This matter points to the electron superconductivity. Those electrons to have equal wave vectors are attracted thus producing pairs and creating an energy gap. It is considered the influence of magnetic field on the superconductor. This explains the phenomenon of Meissner and Ochsenfeld.

Keywords:

Density Matrix, Hamiltonian Model, Electron Distribution, Anisotropy, Electron Interaction, Superconductivity, Energy Gap, Magnetic Field in Superconductivity

Subject Areas: Computational Physics, Theoretical Physics

1. Introduction

Kamerlingh Onnes discovered the phenomenon of superconductivity at Leiden Laboratory, Holland, in 1911 [1] . While investigating dependence of Hg resistance on temperature, he could find that when the material is cooled down to about 4K temperature the resistance drops abruptly to zero. The very phenomenon was called superconductivity. Shortly thereafter, other elements exhibiting similar properties were discovered.

A superconductor is immersed in liquid helium. Initially, weak current is supplied. Then, temperature is reduced. When temperature falls below the defined value, the superconductor circuit is shorted. The superconductor circuit current sustains its steady state as long as it can. A magnetic needle provided as a detector finds some persistent current in the superconductor, thus indicating the magnetic field produced in the solenoid. Temperature T_c, below of which a test piece exhibits its superconducting properties, is called critical temperature.

Shortly thereafter, it was discovered that such superconductivity disappears when a test piece is placed in a relatively weak magnetic field. This phenomenon was discovered by Meissner and Ochsenfeld [2] . Value H_c of the magnetic field in which superconductivity disrupts is called a critical field. Super conductivity continuity disruption is caused by the substance-flowing current that exceeds a particular critical value (Selsby effect). Type-I and type-II superconductors of different properties have been discovered [3] . There are some other experimental superconductivity factors subjected to this description.

Superconductivity was theoretically explained by using the phenomenological expression of the Ginszburg- Landau theory [4] and forty-six years later, upon discovery of the superconductivity phenomenon by Kamerlingh-Onnes, the microscopic theory of this phenomenon was framed by Bardeen, Cooper, and Schriffer [5] . However, many years after my student time, I cannot still understand by what means electrons are distributed over wave vectors k, when the substance superconductivity occurs and where the attraction is coming from with the electrons travelling at equal speeds.

The answer provided is rather simple by its nature. The matter of concern is a density matrix. Electrons are the very particles that make for superconductivity. As for electrons, they are classified as Fermi particles, in other words, defined by the antisymmetric functions. There are pure and mixed states specified by the quantum mechanics. Pure states are defined by the wave functions and mixed states―by the density matrix. When the quantum mechanical system is thermally coupled with a thermostat, the only correct statistical description of the system under analysis is to be considered the density matrix [6] - [13] . Kinetic density matrix equations, as applicable to superconductivity properties, are described in the author’s papers [14] - [25] .

Complete statistical description of the system consisting of the N identical particles is provided in the quantum mechanics by statistical operator 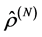to satisfy the normalizing condition as follows:

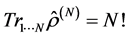(1.1)

This operator can be used for making the hierarchical sequence of operators 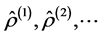defined by the following relation:

(1.2)

where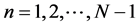. In spite of the fact that statistical operators of the lowest order provide short description of the multi-particle system, only, they are indispensible for their simplicity, particularly when some useful formulae and expressions are virtually required. This kind of a short description makes it possible to express all observable physical quantities that characterize the macroscopic system state exactly or approximately by using operators 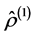and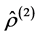, or one-particle operator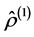, only. The one-particle statistical operator can be found by the following formula:

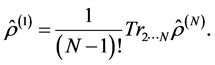(1.3)

The one-particle matrix exposed to particular α-representation can be formulated as follows:

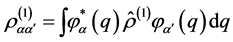(1.4)

where 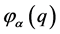is the wave function; α is the quantum number system under which the state of one particle is specified;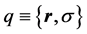, r is the particle radius vector, σ is the spin variable.

As follows from some methods, one-particular statistical operator can be found and applied for the equilibrium system, whether individually or together with operator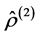, by using the variational principle taking into account the properties of some thermodynamic quantities to possess an extreme value when the multi- particular system is in the static equilibrium state. The equation for the wave vector electron distribution function can be solved hereunder by using the variational method.

2. Internal Fermion System Energy

The system consisting of N-identical Fermi particles can be shortly described by using one- and two-particle density matrixes:

(2.1)

One-particle density matrix satisfies the following normalizing condition:

(2.2)

where is the probability of filling the state α.

The exact expression of the internal energy of the identical particle system can be written by using the density matrix (2.1) as follows:

(2.3)

Here and are matrix elements of one-particle Hamiltonian and the Hamiltonian of the interaction of two particles, respectively:

(2.4)

Density matrix is antisymmetric, that is:

(2.5)

Consequently, matrix elements subject to the above expression (2.3), we also consider antisymmetric, that is:

(2.6)

The transition from the coordinate representation, in which Hamiltonians are usually defined, to particular α-representation is performed using the orthonormal system of wave functions. As referred to these functions, the matrix elements of the Hamiltonians (2.4) can be calculated by using well-known formulae as follows:

(2.7)

(2.8)

where the integral symbol points out integration over the coordinates and indicates summation over the spin variable; Φ₁₂ is a Slater two-particle wave function:

(2.9)

Substituting this function into formula (2.8), we obtain the following antisymmetric matrix:

(2.10)

where

(2.11)

is the potential energy of interaction between two fermions.

Provided that the two-particle density matrix applicable to the fermion system is antisymmetric, we can accept the following approximated expression:

(2.12)

Substituting this expression into formula (2.3), we can formulate the following expression:

(2.13)

that meets the medium field approximation.

3. Entropy

There is a representation in which the single-party density matrix is diagonal, i.e. it has the form as follows:

(3.1)

where n is a set of quantum numbers, which determines the state of one particle under the new representation; are the diagonal elements of the density matrix; is a Kronecker symbol. By definition, value points to the probability of occupation of state n by one of the particles. Thus, the function describes the distribution of particles over states and satisfies the normalization condition as follows:

(3.2)

Transition from n-representation to α-representation that specifies the matrix elements (2.4) of Hamiltonians and is performed by using a unitary transformation approach:

(3.3)

where is the unitary matrix;

(3.4)

Using the distribution function we can write down the well-known approximated expression for the entropy of the fermion system:

(3.5)

4. Variational Principle

Referring to formulae (2.13), and (3.5), we can state that free energy, subject to the assumed approximation, is the w_n and dependent functional. Since the equilibrium state of the system corresponds to the minimum free energy value at fixed temperature T and volume V, functions and can be found by minimizing the free energy subject to conditions (3.2) and (3.4). By this means, we encounter the problem of the conditional extremum solved by employing the following auxiliary Langrange-method functional:

(4.1)

where μ and are undetermined multipliers. Extremum conditions for the functional where μ and are undetermined multipliers. Extremum conditions for the functional

(4.2)

lead to the following distribution function w_n and unitary matrix equations:

(4.3)

(4.4)

where is the mean energy of one particle:

(4.5)

(4.6)

is the kinetic energy of a particle,

(4.7)

is the effective one-particle Hamiltonian as defined in the mean-field approximation:

The solution is significantly easier in the case when the properties of the system under analysis make it possible to predict what representation is used to bring the density matrix to its diagonal pattern. As applies to this case, it is time to solve the Equation (4.3). Any solutions sourced from the above equation can exhibit certain interesting features related to its nonlinearity and particular dependence of kernel on quantum numbers n and. The aim of this chapter is to study such features and their physical effect.

5. Statistical Description of the Electrons in the Crystal Lattice

The arrangement of atoms within a given type of crystal can be described in terms of the Bravais lattice with location of the atoms in an isolated unit cell specified. We shall determine position of one of the atoms in the unit cell using vector R and arrangement of all other atoms in the cell relative to the first one―using vector a. Let s be a set of quantum numbers defining the wave function of one of the states of an electron located within the neighborhood of the atom, the position of which is determined by vector R + a. By using the available notations, we write the orthonormal system of wave functions that define localized electron states in the form as follows:

where is a set of quantum numbers that determine the state of the electron in the crystal lattice. In this case, the Vanier functions are preferable to use for these functions. Using these functions, we can calculate the matrix element of the Hamiltonians (2.7) and (2.8).

Using the method proposed in the previous section, the density matrix of equilibrium state of the system of electrons within a crystal can be found. Some of the simplest types of Hamiltonians only that simulate interaction and behavior of conduction electrons in real metals to the extent of a particular precision will be analyzed in this chapter.

We consider the cases when one atom (a = 0) only is in the unit cell and assume that the valence electron matrixes (2.7) and (2.11) have the form as follows:

(5.1)

where parameter s takes on finite number G of different values;

(5.2)

is the averaged wave function that defines an electron located within the neighborhood of site R; is the potential Coulomb-based two electron repulsion energy. In this case, the density matrix describing conduction electrons is expressed as follows:

(5.3)

Using formulae (5.1), (5.3) and making some simple transformations, the electron energy (2.13) can be expressed as follows:

(5.4)

where;

. (5.5)

If the electrons are distributed over the sites of the crystal lattice evenly, than the density matrix can be formulated as follows:

(5.6)

where the summation is performed by using vectors k of the first Brillouin zone; N_L is number of lattice sites; is a wave vector electron distribution function that satisfies the following normalizing condition:

(5.7)

v is the extent to which the zone is filled:.

With the expression (5.6) substituted in the formula (5.4), the following expression can be obtained:

(5.8)

where is the kinetic electron energy:

;

is the energy of interaction of two electrons with wave vectors and:

(5.9)

The equality (5.6) is, in its essence, the unitary transformation that diagonalizes the density matrix. In this case, the formula (3.5) takes on the form as follows:

While minimizing free energy subject to the normalizing condition (5.7), we can obtain the equation that makes it possible to find the wave vector conduction electron distribution function that is of similar nature as the Equation (4.3):

(5.10)

where is the mean energy of one electron with wave vector k:

(5.11)

Now, we can refer to the formula (5.9) to determine the structure of the kernel in the functionals (5.8) and (5.11). Since diagonal elements are the greatest ones of the matrix elements (5.9), as complies with and, we can use an approximated formula as follows:

(5.12)

where is the mean energy of Coulomb interaction of two electrons localized at the sites and the second summand approximates the off-diagonal elements. In the strict sense, the function U⁽⁰⁾ in the formula (5.12) should depend not only on, but also on. Using formulae (5.5), (5.8), (5.9), and (5.12) we obtain the following approximate expression for interaction energy of electrons:

(5.13)

where

(5.14)

(5.15)

The first summand expressed in the formula (5.13) is the energy of direct Coulomb electron interaction that does not depend on the distribution function. The following summand represents the exchange energy of electrons. The kernel in the above sum is a positive function that takes on the largest value at and rapidly decreases against increase of the as a result of long-range Coulomb interaction behavior. Since the exchange energy is negative, such behavior of the function makes for effective attraction to occur between electrons with the nearest wave vector values. As applies to the positive summands expressed in the formula (5.13) that contain values I_k, they simulate effective repulsion of k and ?k wave vector electrons. The mean one-electron energy (5.11) that corresponds to the interaction energy (5.13) can be formulated as follows:

(5.16)

Unfortunately, while using the formula (5.14) or (5.15), it is impossible not only to find any analytical solution of the Equation (5.10), but also to study it in details. Therefore, we approximate the function (5.14) by using the following expression:

where J is a positive constant; and the value (5.15) can be considered as that does not depend on a wave vector:

As applies to this case, the formula (5.16) takes on the following expression:

(5.17)

and the energy of two electron interaction with wave vectors and takes on the following expression:

(5.18)

6. Electron Wave Vector Distribution Function

The formula (5.17) can be used for transforming the Equation (5.10) as follows:

(6.1)

In this equation, we substitute k for −k. Since, we can obtain the following expression:

(6.2)

Equations (6.1) and (6.2) result in the following combined equations for two values and of the electron distribution function:

(6.3)

We can demonstrate that this system admits two types of solutions. One of them describes isotropic wave vectors distribution of electrons and other―anisotropic wave vectors distribution of electrons. If

(6.4)

then each of the Equation (6.3) transformed can be formulated as follows:

(6.5)

If I = J, this equation is solvable as the Fermi-Dirac function.

The unknown functions and, expressed via Equation (6.3), admit as combined functions where the kinetic electron energy acts as a intervening variable: and. The functions and are solvable as follows:

(6.6)

where

(6.7)

energy ratio I and J defined by the parameter

(6.8)

In this chapter, we will study the case when the parameter J = 3I; in this case f = 1/2.

7. Anisotropy

We have prescribed function f = f(a), i.e. value f depends on vector a. If value f depends on modulus of this vector a, only, the distribution concerned is called isotropic, i.e. it may be formulated as f = f(a). We will depict a sphere of radius a centered in the origin of coordinates. So, value f will remain equal at any point of this sphere, providing that f = f(a) is the isotropic function. Any other f = f(a) function will be referred to the anisotropyone.

Now, we will consider the example of the anisotropic function. We will depict two vectors. One of them will be an arbitrary vector a and the other one will be rated as equal, but opposite in its direction −a. So, if it is appeared that function values fail matching in the points concerned, i.e.

(7.1)

this function will be called the anisotropic one.

8. Isotropic Distribution of Electrons

We express the combined Equation (6.6) regarding the case when no anisotropic condition is available, i.e. w₁ = w₂ = w₀. Now we can obtain the following equation:

(8.1)

This function is graphically represented in Figure 1.

9. Anisotropic Distribution of Electrons

With the electrons being distributed over wave vectors in the anisotropic manner, we will introduce new variables d and s by means of the following relations:

(9.1)

Without loss of generality, the difference d of two values w₁ and w₂ of the distribution function can be considered as a nonnegative value: d ≥ 0,

. (9.2)

In this case, the largest value d equals to one:. Value s can take on those to be ranged from −1 to 1:. Now, we solve Equation (9.1) relative to the probabilities w₁ and w₂:

(9.3)

Using the formulae (9.3), we transform the combined Equation (6.6). For this purpose, we at first subtract one equation from other and then sum them up. As a result, we can obtain the following combination:

(9.4)

The first equation of the above combination is easily to solve in relation to s:

. (9.5)

As provided by the relations (9.3) hereinabove, the probabilities w₁ and w₂ can be considered as the functions of parameter d:,. The second combined Equation (9.4) makes it possible to express the electron energy by using parameter d. As based on the obtained dependencies, it is easy enough to plot the function graphs and for various temperature values. Such anisotropic curve graphs are demonstrated in Figure 2. Many-valuedness of the function proves that various equilibrium states of conduction electrons in metals are possible at the same temperature. These macro-states are different from those represented by the Bloch electron distribution function. As a matter of the fact, it is the electron minimum energy macro-state that can be actually implemented provided, that this kind of state is rather stable and it is kept out of any disruption under external effects.

The plots, demonstrated in Figure 1 and Figure 2, provide a particular insight into electron state distribution pattern shaped up under various metal temperatures. When temperature τ ≥ 1, the isotropic electron wave vector distribution only is possible that is described by the function. The function graph curve stated against all temperature values passes point Ω at the coordinates of and. When the temperature falls down (), the curve slope at this point is increased. When temperature drops down to rather low values, the dependency curve is bent so that it looks like letter Z.

A closed anisotropic curve originates at point Ω of the curve at τ = 1 and its dimensions increase against the falling temperature. The curve shape also changes. The following critical temperature corresponds to value τ = 1:

(9.6)

If values are used, where is a certain critical value, the vertical straight line meets an anisotropic curve maximum at two points (curve 2 in Figure 2(a)). If, the anisotropic curve Z bends so that the vertical straight line cuts it at four points (curve 1 in Figure 2(a) and Figure 2(b)). The anisotropic curve Z transforms to a polygon at τ → 0. As a result, the AB₁C₁OC₂B₂A polygon line resembles letter Z. This polygonal line is shown in Figure 2(c).

10. Electron Distribution at T = 0

Now, we consider the electron distribution function at T = 0 in details. Within the range of τ → 0, the isotropic distribution solvable by the Equation (8.1) is expressed as follows:

(10.1)

This dependence is graphically represented in Figure 1.

Within the range of τ → 0, as stated by the Equation (9.4), the following occupation probability dependence w of the kinetic electron energy ε that describes anisotropic electron wave vector distribution can be formulated:

(10.2)

where i = 1 or 2. So, the values of functions and produce the following pairs:

(10.3)

at, or

(10.4)

at, or

(10.5)

at.

As demonstrated in Figure 2(c), the AB₁C₁O polygonal line meets the relationship and the AB₂C₂O polygonal line―the relationship.

11. Electron Energy Calculation at T = 0

Now, we calculate the energy of electrons distributed isotropically or anisotropically. For this purpose, we use the normalizing condition that can be expressed by the following equation:

(11.1)

The electron system energy, when approximated in the mean field, takes on the following expression:

(11.2)

As the distribution function w = w(ε) is known, we can find chemical potential and electron energy at T = 0. Such calculations are demonstrated in the previous papers [18] - [23] . In fact, it is macro-state of the electron energy minimum that can be actually implemented. The energy calculated at T = 0 is the lower-range one regarding the condition described by the following formula:

(11.3)

This function is anisotropic at.

We approximate the dependence of the kinetic electron on the wave vector k formula

(11.4)

where m is the effective mass of the valence electron. Instead of summing k will produce the integration of the kinetic energy of of the electron.

Using the relation (11.3), we obtain the normalizing condition to a symbolic equality

(11.5)

where, V―the crystal volume, N―the number of valence electrons. In this case, the normalizing condition results in the following equation:

(11.6)

and the energy follows that

(11.8)

12. Superconducting Electron State

The distribution function is a single-valued one. This means that one value of the distribution function shall correspond to one value of the energy. As concerns the anisotropic distribution function, it is two-valued. It simultaneously determines two values of the wave vectors k and −k, to which two values of the distribution function and are conformed. However, whether the values and can be conformed to the above vectors. In this case, the superconductivity phenomenon is examined.

For detecting superconductivity, initially weak current is supplied to a conductor. Then, temperature is reduced. When temperature falls below the defined value, the superconductor circuit is shorted. The superconductor circuit current sustains its steady state as long as it can. Let current flows along axis x. Than at T = 0, the following electron wave-vector space distribution function k can be represented in Figure 3.

13. Electron Mean Energy

Dependence of the electron mean energy against kinetic energy can be found by the formula (5.17):

(13.1)

(13.2)

This dependence, as rated at various temperatures τ, is graphically represented in Figure 4. At T < T_c, each of the curves has a “well” conforming to values of the kinetic energy anisotropy ε, that satisfies the inequalities as follows:

. (13.3)

Value is the lower-range value of the kinetic electron energy subject to functions and. Value satisfies the following condition:

(13.4)

according to which the “well” edges, represented by the graphic chart, are shown at the same level. However, there is an opening on the well edge’s right. This means that there is a certain “gap” in the spectrum of values of the electron energy. The energy gap width ∆ extends from zero to value J, when temperature falls down from T_c to zero. The well width

(13.5)

is also extended from zero to value I at T = 0.

14. Real-Valued Distribution Function

The lower-range electron energy corresponds to the real-valued equilibrium distribution function. The real-valued equilibrium distribution function follows from the electron energy calculated for various distribution functions. The function curve, as rated against τ = 0.75, is shown in Figure 5.

15. Type-I and Type-II Superconductors

For characterizing type of a superconductor, the following parameter value is involved:

(15.1)

We express parameter ζ in terms of parameter f. Now, we can obtain the following formula:

(15.2)

This function is graphically represented in Figure 6. Using known inequalities, we can write the superconductor type condition. The condition indicates to a type-I superconductor. And the condition indicates to a type-II superconductor. These conditions have been originally gained by A. A. Abrikosov.

Parameter f = −1 shows that value of J = 0, that characterizes the gap width ∆, does not produce any pair. Consequently, the coherent length ξ (i.e. electron pair interaction length) equals zero, as well. As applies to this case, the condition ξ < λ satisfies where λ is the superconductor magnetic field penetration depth. This condition shows that the type-II superconductor is in the range of the f parameter-defined values.

16. Density Matrix

Now, when we find the probability w_k, it is possible in principle to find the density matrix. Using a unitary transformation, we have

. (16.1)

Unfortunately, the calculations carried out at arbitrary temperatures are very complex. The density matrix can be calculated only for the probability of (11.3) at the temperature T = 0:

(16.2)

17. The Meissner and Ochsenfeld Effect

When a specimen is put in a relatively weak magnetic field superconductivity vanishes. Such phenomenon was discovered by Meissner and Ochsenfeld [2] . Magnetic field strength at which superconductivity is destroyed is known as the critical field. Temperature dependence of the critical field is described by the following empirical formula:

(17.1)

where is the magnetic field strength at absolute zero of temperature T = 0. The dependence (17.1) is plotted in Figure 7.

The plane (H, T) is represented by a superconductive state phase diagram. Asdemonstrated in Figure 7, the substance in superconductive state S is found under the curve and that to be in normal state N―above the curve. Any superconductor introduced by such state diagram is known as the type-I superconductor. We will hereafter consider the superconductors of such type only.

18. Magnetic Field in Superconductor

With an electron having a spin, Hamiltonian, in the presence of a magnetic field, will be expressed as follows:

(18.1)

where is a spin magnetic moment of an electron; is a Bohr magneton; is an electron spin; U(r) is potential electron energy; is magnetic field strength.

Let’s a wave function will be written as follows:

(18.2)

where is a coordinate function; R is a vector defining the ion around which an electron moves; is a spin function;;. Let’s assume that functions are mutually

equal:. Spin functions only are different. Thereafter, we will obtain two following functions:

(18.3)

In this case, matrix elements of the one-body Hamiltonian may be written by using the following expression:

(18.4)

If we substitute formula (18.4) herein, we will obtain the following expression:

(18.5)

Density matrix is transformed to the diagonal form by means of the following unitary matrix:

(18.6)

where. Hence, density matrix turns to the matrix as follows:

(18.7)

After simple transformations we will obtain the expression of the non-interacting electron energy:

(18.8)

where,

(18.9)

(18.10)

On adding the above formula to the energy of interacting electrons, we can obtain the following electron energy expression:

(18.11)

With thermodynamic potential Ω minimized taking into account the energy (11), we will come to the following integral equation applicable for finding the distribution function w_k of wave-vector conduction electrons when a specimen is exposed to a magnetic field:

(18.12)

Let’s assume that

(18.13)

Then, the distribution function equation will take up the previous solution:

(18.14)

Now, we shall consider the case when a magnetic field destroys superconductivity at T = 0. The valence electron energy is herein expressed by the formula (11). If a superconductor is not exposed to a magnetic field, the real distribution function takes up the form shown in Figure 8.

Let’s assume that the magnetic field strength is expressed as follows:

(18.15)

where is the width of the potential well on the average electron energy to kinetic energy curve as specified at zero temperature. Hence, the graph of the distribution function is shifted on the right by the above value (see Figure 9).

With the distribution function taking up the following formula, superconductivity vanishes:

(18.16)

In this case, the normalizing condition results in the following equation:

(18.17)

it follows that

(18.18)

The valence electron energy (18.11), wherein J = 3I and L = I, may be calculated by the following formula:

(18.19)

As a result, we shall obtain the following expression:

(18.20)

But should the superconductivity state be survived and the distribution function is expressed as follows:

(18.21)

The distribution function can be found real, if the electrons possess less energy. As for the function (18.21), the normalizing equation takes up the following form:

(18.22)

This equation yields the following chemical potential:

(18.23)

In view of the expression formulated here in above (18.11), the electron energy may be calculated by means of the following formula:

Let’s assume that J = 3I and L = I. Then, we will obtain the formula as follows:

(18.24)

On calculating, the formula below is obtained:

(18.25)

Now, we can find the energy differential:

(18.26)

As seen, energy of state that is produced by the superconductivity-destroying magnetic field occurs to be less than energy of the superconductive state:

(18.27)

This means that any superconductivity exposed to a magnetic field vanishes.

19. Magnetic Field Strength

We take parameter L as equal to I. In this case, the distribution is displaced on its right. Now we will find the critical magnetic-field strength at T = 0:

(19.1)

If temperature τ is above zero, than the critical magnetic-field strength, as referred to the formula (9), can be formulated as follows:

(19.2)

where is the width of a potential well (13.5) on the average electron energy to kinetic energy curve as specified at temperature τ.

If to refer to a theoretical average electron energy to kinetic energy curve demonstrated in Figure 4, specific temperature dependence curve of the critical magnetic-field strength is plotted. Such curve is shown in Figure 10.

With the curve in Figure 7 compared against that shown in Figure 10―i.e. experimental dependence of the critical field strength upon the theoretical one―it is found that the both curves perfectly match each other. But the following relation

(19.3)

may be used for measuring the width of an energy well.

20. Conclusions

The model for electrons in metal, described in this paper, can be assumed as a basis of an alternative theory of superconductivity. This model significantly differs from those which have been applied in the contemporary theory of superconductivity. The superconductivity, described herein, is caused by repulsion of wave vector k and −k electrons, but electron pairs and energy gap in the spectrum―by attraction between the electrons of equal wave vectors. Electrons are statistically described in terms of the density matrix formalism, featured with the simplicity representative by specific formulae and physical content. The problem examined demonstrates advantages of the density matrix method.

In this paper we consider that critical magnetic field removes the superconductivity. It is shown that this is due to the width of the hole in the dependence of the average energy of an electron from its kinetic energy. This connection can be used for the experimental dependence of the width of the hole on the temperature.

Cite this paper

Boris V. Bondarev, (2015) New Theory of Superconductivity. Method of Equilibrium Density Matrix. Magnetic Field in Superconductor. Open Access Library Journal,02,1-20. doi: 10.4236/oalib.1102149

References