Journal of Materials Science and Chemical Engineering
Vol.04 No.07(2016), Article ID:68979,8 pages
10.4236/msce.2016.47009
Damping Factor Estimation of a Flexible-Matrix-Composite Body Pump
N. P. Kumar, H. Ghoneim
Mechanical Engineering, Rochester Institute of Technology, Rochester, NY, USA



Received 12 May 2016; accepted 21 July 2016; published 25 July 2016

ABSTRACT
Two very important factors which determine the effectiveness of a pump are its volumetric and power efficiencies. Yin and Ghoneim constructed a prototype of a Flexible-Matrix-Composite (FMC) body pump with a very high volumetric efficiency or pumping potential (the relative volume reduction due to a relative input stroke). The high volumetric efficiency is attributed to the geometry of the pump’s structure (hyperboloid) as well as the high negative effective Poisson’s ratio of the 3-layer [θ/β/θ] flexible-matrix-composite (carbon/polyurethane) laminate adopted for the body of the pump. However, the power efficiency of the pump was not evaluated. It is the objective of the current paper to obtain an estimate of the power efficiency of the pump. The viscoelastic properties of the 3-layer FMC (carbon/polyurethane) laminate are evaluated experimentally using the Dynamic Mechanical Analyzer (DMA) as well as analytically by applying the correspondence principle together with the micro-mechanics approach. In order to obtain an estimate of the power efficiency of the FMC body pump, the axial and shear loss factors of a laminated infinitely long cylindrical tube as functions of β and θ fiber orientation angles are determined employing the Adam and Bacon approach. The analysis engenders high loss factors (greater than 0.4), which suggests that the power efficiency of the proposed pump using the 3-layer carbon/polyurethane laminate may be low.
Keywords:
Flexible-Matrix-Composites, Dynamic Mechanical Analyzer, Viscoelastic Characteristics, Damping Factor

1. Introduction
Flexible-Matrix-Composites (FMCs) are the branch of composite materials where the matrix is made of a compliant material (rubber, polyurethane, silicon). Flexible-matrix-composites have found a wide range of applications including flexible body pumps and vibration isolation mounts. The diaphragm pumps, the jellyfish-inspired flexible pump [1], and the left-ventricle-like pump [2] are examples of compliant-body pumps. Yin and Ghoneim constructed a prototype of a flexible body pump with a very high volumetric efficiency or pumping potential (the relative volume reduction due to a relative input stroke) [3]. The high volumetric efficiency is attributed to the geometry of the pump’s structure (hyperboloid) as well as the high negative effective Poisson’s ratio of the 3-layer [q/b/q] FMC (carbon/polyurethane) laminate adopted for the body of the pump. The power efficiency was not evaluated. The tunable fluidic composite mounts [4] and the controllable suspension system invented by Carlson et al. [5] are examples of the application of FMC in vibration isolation devices. In both practices (pumps and mounts) the FMC material is subjected to a dynamic loading and quantifying the inherent damping, as a function of frequency, is important. Damping should be minimized in the pumping applications to minimize energy losses and thereby improve the power efficiency. On the other hand, higher damping in general is preferable for vibration isolation applications in order to dissipate more of the excessive energy of vibration.
An attempt to find the overall loss factor (extensional and shear) of the 3-layer [q/b/q] FMC (carbon/polyu- rethane) laminate (plate) was undertaken by Kumar et al. [6]. The viscoelastic properties (complex extensional and shear moduli) of the polyurethane matrix were determined using the Dynamic Mechanical Analyzer (DMA). The micromechanics approach was employed to estimate the in-plane viscoelastic properties of the lamina: the Rule of Mixture for the longitudinal modulus and the Poisson’s ratio; and the Concentric Cylindrical Model for the transverse and shear moduli. Then, the Adam and Bacon lamination theory was applied to predict the axial and shear loss factors of the laminate. It should be mentioned that there was a considerable difference between the experimental and analytical results and consequently, the experimental work was omitted and the study presented in general was subjective.
The objective of the current work is two folds: to obtain a better estimate of the viscoelastic properties of the carbon/polyurethane (C/PU) laminate employed for the body of the novel pump; and to estimate the axial and shear loss factors of the 3-layer [q/b/q] laminated cylindrical tube as functions of the angles q and b. These loss factors are good estimates of the inherent damping in the C/PU cylindrical tube, and consequently are good indicators of the power efficiency of the flexible body pump adopting this 3-layer laminate.
2. Carbon/Polyurethane Viscoelastic Characterization
2.1. Lamina
Following the method adopted in the previous work [6], the dynamic viscoelastic characteristics of the carbon/ polyurethane (C/PU) laminas are determine in two steps: 1) experimentally determine the dynamic complex extensional and shear moduli of the polyurethane (PU) matrix material (PMC® 121-31 urethane rubber) using the DMA (Perkins Elmer DMA 8000), and 2) apply the correspondence principle together with the micro-mechan- ics approach, assuming that the carbon fibers behave purely elastic, to estimate the viscoelastic dynamic properties of the C/PU lamina [7]. These dynamic properties are the complex effective longitudinal and transverse moduli 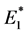 and
and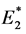 , respectively, the complex effective in-plane shear modulus
, respectively, the complex effective in-plane shear modulus 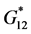 and the effective in-plane Poisson’s ratio
and the effective in-plane Poisson’s ratio 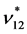 . In addition, experimental work is conducted to determine the complex transverse and shear moduli, and a comparison of the analytical results with the corresponding experimental ones is presented and discussed.
. In addition, experimental work is conducted to determine the complex transverse and shear moduli, and a comparison of the analytical results with the corresponding experimental ones is presented and discussed.
The DMA measures the variation of the storage and the loss moduli of viscoelastic materials as functions of frequency over a range of temperature. The temperature-frequency superposition principle is applied to generate a master curve [8], which represents the variation of the moduli versus the “reduced” frequency, faT. The superposition principle uses a shift factor aT to collapse the moduli’s curves at various temperatures into the master curve. In this analysis the William-Landel-Ferry (WLF) equation is selected for the shift factor:
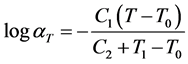 , (1)
, (1)
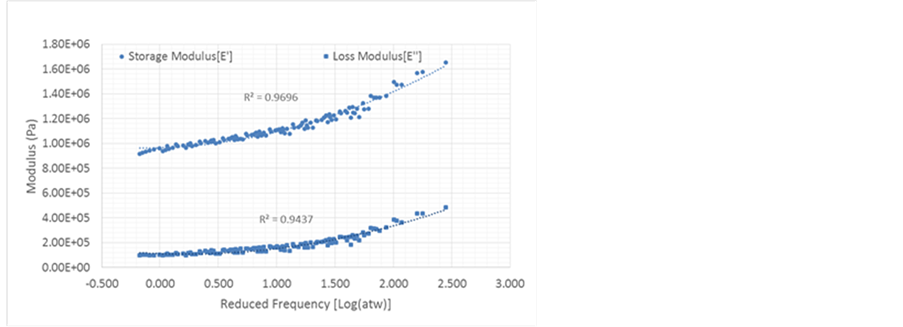
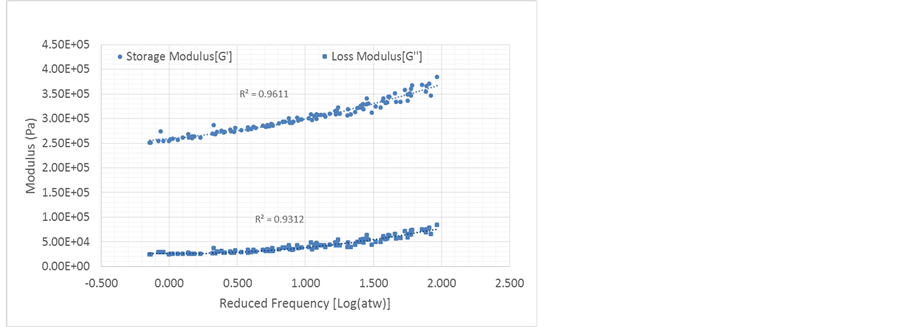
where C1 and C2 are material constants to be determined experimentally, and T and T0 are the temperature and reference temperature, in Kelvin, respectively. In this work, the reference temperature is taken as the room temperature (288 0K). Typical examples of the measured moduli (storage and loss shear and extensional) of the polyurethane as functions of the reduced frequency are displayed in Figure 1 and Figure 2, respectively. The frequency was swept from 1 to 100 Hz, over a temperature range of 0˚C - 30˚C. The complex shear (G*) and extensional (E*) moduli are, respectively, given by:
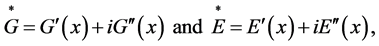 (2)
(2)
where G' is the shear storage modulus, G'' is the shear loss modulus, E' is the extensional storage modulus, and E'' is the extensional loss modulus. All the four moduli are approximated by a quadratic polynomial fit (dotted lines in Figure 1 and Figure 2); that is, E = a2 x2 + a1x + a0, where E stands for any of the four moduli, and x = log(αTf) . The values of the material constants a2, a1, a0, C1 and C2 are displayed in Table 1. Since the measurement of the Poisson’s ratio requires different experiments, which are not available, the Poisson’s ratio of the PU
is estimated from the relationship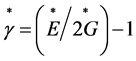 . Tschoegl et al. [9] cautioned against the calculation of the
. Tschoegl et al. [9] cautioned against the calculation of the
frequency/time dependent Poisson’s ratio by combining response functions such as E*(ω) and G*(ω). They stated that the determination of any bulk functions by calculation from any other parameters requires the source parameters to be obtained using a strict protocol known as the standard protocol [9], which is extremely difficult to achieve. In any case, it turned out that the effect of the Poisson’s ratio on the work done is marginal.
With the complex shear and extensional moduli of the polyurethane (PU) matrix material known, and with the assumption of purely elastic behavior for the carbon fibers (Ef = 231 GPa, and nf = 0.2), the in-plane viscoelastic
Figure 1. The extensional storage and loss moduli of PU.
Figure 2. The dynamic shear storage and loss moduli.
Table 1. Material properties of the shear and extensional moduli of PU.
properties of the C/PU lamina can be evaluated using the principle of correspondence and the micromechanics approach. It should be understood that the composite lamina is assumed to be transversely isotropic [10]. In the current work, the rule of mixture is applied for the evaluation of the effective longitudinal complex modulus (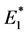 ) and the effective in-plane Poisson’s ratio (
) and the effective in-plane Poisson’s ratio (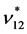 ), and Halpin-Tsai model for the effective transverse complex modulus (
), and Halpin-Tsai model for the effective transverse complex modulus (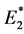 ) and the effective in-plane shear modulus (
) and the effective in-plane shear modulus (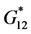 ) [11]; That is,
) [11]; That is,
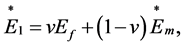 and
and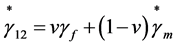 ,
,
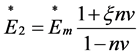
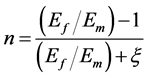
where v is the fiber volume fraction, x is a curve fitting parameter, which is also a measure of the reinforcement of the matrix by the fibers, and the subscripts m and f stand for the matrix and fiber, respectively.
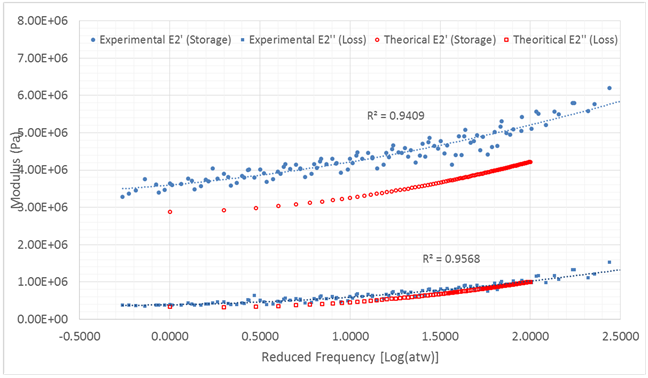
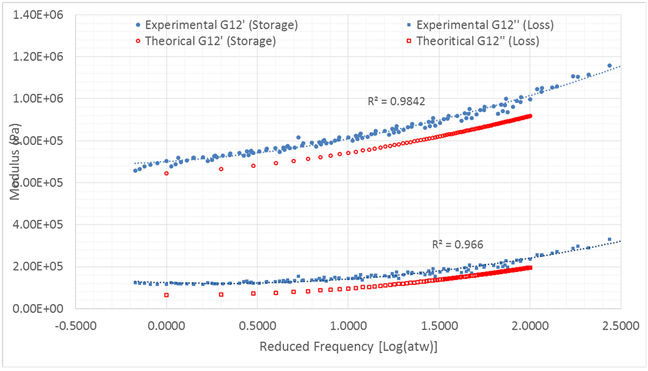
Figure 3 and Figure 4 show the predicted complex (storage and loss moduli) in-plane transverse and shear moduli, respectively, of the C/PU lamina. The corresponding experimental results are also included for comparison. The experimental results of the extensional and shear moduli are approximated, as in the case of the polyurethane matrix, by a quadratic polynomial. The reference temperature T0 is taken as 288 0K, and the curve fitting parameter x = 2 for the calculation of the shear modulus and x = 3 for the transverse modulus.
Figure 3. Experimental and analytical complex transverse modulus of C/PU lamina.
Figure 4. Experimental and analytical complex shear modulus of C/PU lamina.
2.2. Laminate
The correspondence principle in combination with the classical lamination theory has been employed to calculate the global longitudinal, transverse and shear complex moduli of C/PU laminates.
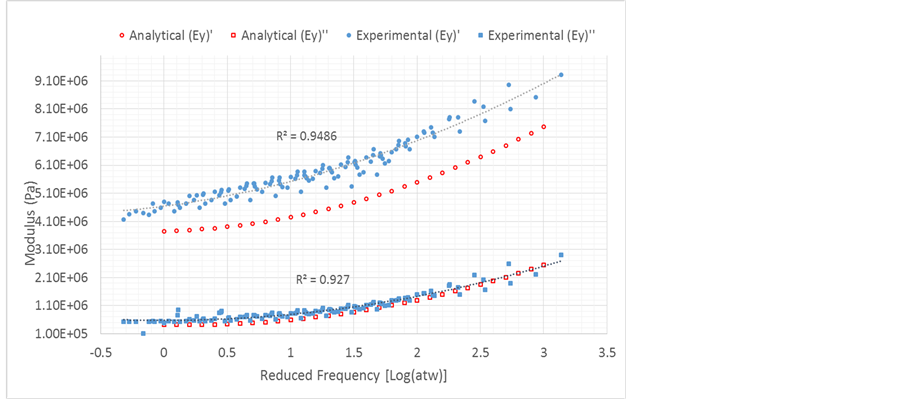
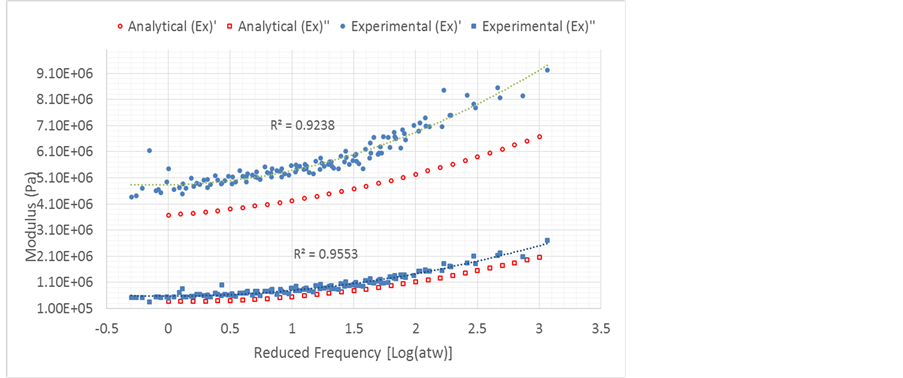
The analytical results for some laminates with moduli that satisfy the upper limit measurement of the DMA are compared with the corresponding experimental results. Samples of the results are shown in Figure 5 and Figure 6. Figure 5 displays the transverse complex modulus results of a [5/35/5] laminate. The extensional complex modulus is presented for a [30/-60/30] laminate in Figure 6. Clearly, Figures 3-6 show that the analytical results for all cases consistently underestimate the experimental results. Following are the main contributors to this discrepancy:
・ The application of the simple micromechanics theories of the Rule of Mixture and Halpin-Tsai.
・ The testing specimens were manually produced and despite the meticulous care taken, the quality of the specimens, in particular the accuracy of the fiber angle orientation and perfect wetting and bonding, was limited.
・ The shear test involves applying an optimum pressure to hold the test specimen by gently squeezing it between two plates [12]. Applying the optimum pressure presented a major challenge.
Figure 5. Experimental and analytical complex trans-verse modulus of a C/PU [5/35/5] laminate.
Figure 6. Experimental and analytical complex extensional modulus of a C/PU [30/-60/30] laminate.
3. Effective Damping Properties
The correspondence principle, in combination with the classical lamination theory and the method employed by Adams and Bacon [13], is adopted for the evaluation of the overall effective damping of a laminate. According to Adams and Bacon’s method the overall effective damping is represented by the laminate effective loss factor h. It depends on the type of loading. In the current work, the effective extensional and shear loss factors h of the laminate are considered. In general, the effective loss factor h is given by
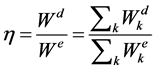
where We is the total elastic strain energy per cycle of loading, Wd is the total dissipated energy per cycle, and k is the layer (lamina) number. If W is the total work done per cycle, then
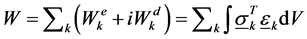
where sk, and ek are the in-plane stress and strain vectors in the material coordinates, respectively. An estimate of the extensional and torsional loss factors of the hyperboloid FMC body pump can be realized by analyzing an infinitely long laminated cylindrical tube subjected to axial and torsional loading, respectively.
Herakovitch [14] presented an exact solution of an elastic laminated long tube under the effect of applied axial load, torque, internal and external pressures. It can be extended to viscoelasticity via the application of the correspondence principle. For a specific kind of loading, the stress and the strain vectors in the global coordinates can be determined, the stress vector in the material coordinates can be computed for any fiber angle orientation, the strain energy (elastic and dissipated) can be computed using (5), and consequently applying (4) the effective loss factor of the laminate for a specific loading can be evaluated [6]. Following these steps, a Matlab program is developed for the viscoelastic frequency response analysis of a laminated long tube, and employed to calculate the extensional (due to applied axial force) and torsional (due to applied torque) loss factors of a [q/b/q] 3-layer tubular laminate.
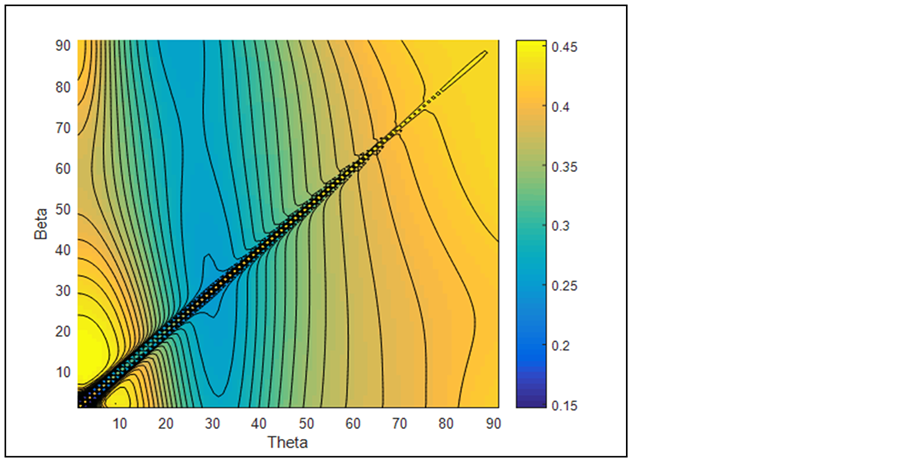
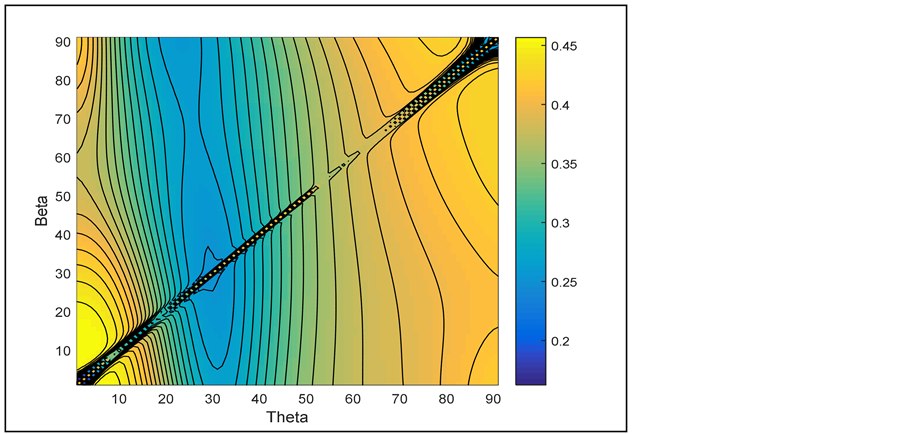
Figure 7 and Figure 8 display the color map plot of the effective axial and shear loss factors for the [q/b/q] 3-layer laminated tube, respectively. The following can be deduced:
・ In the vicinity of q = b (diagonal lines) the effective damping experiences a very high gradient (any slight deviation from q = b renders a huge change in h). Consequently, this region is impractical for h-based design.
・ The loss factor is influenced mainly by the fiber orientation angle of the outer q-layers.
Figure 7. Color-map plot of the effective extensional loss factor (laminated tube).
Figure 8. Color-map plot of the effective shear loss factor (laminated tube).
・ The 3-layer tubular laminate exhibits a very high inherent damping factor (h > 0.4). In general, the results indicate that there is no practical fiber angle orientation, which may render low loss factor (h < 0.01). More specifically, the results clearly confirm that the fiber-angle orientation, which renders a high negative Poisson’s ratio [5/40/5] and selected for the design of the flexible body pump [3], is associated with high damping.
4. Conclusion
The viscoelastic properties of the FMC carbon/polyurethane (C/PU) laminate, adopted for the body of the novel pump proposed by Yin and Ghoneim, are estimated experimentally using the Dynamic Mechanical Analyzer (DMA) as well as analytically applying the correspondence principle together with the micro-mechanics approach. The agreement between the predicted viscoelastic properties of the C/PU laminates and the corresponding experimental ones, in general, is fair. In addition, the loss factor of the 3-layer [q/b/q] laminate is estimated employing Adam and Bacon approach. More specifically, the axial and shear loss factors of a laminated infinitely long cylindrical tube as functions of b and q fiber orientation angles are determined. It is found that, in general, the 3-layer [q/b/q] laminated cylindrical tube exhibits high axial and shear loss factors and consequently may render a low power-efficiency pump.
Cite this paper
N. P. Kumar,H. Ghoneim, (2016) Damping Factor Estimation of a Flexible-Matrix-Composite Body Pump. Journal of Materials Science and Chemical Engineering,04,59-66. doi: 10.4236/msce.2016.47009
References
- 1. Nawroth, J. and Dabiri, J. (2010) Fluid Transport in Muscular Pumps at Intermediate Reynolds Numbers. 63rd Annual Meeting of American Physical Society, Division of Fluid Dynamics, Long Beach, Vol. 55.
- 2. Chanda, A. and Ghoneim, H. (2015) Pumping Potential of a Two-Layer Left-Ventricle-Like Flexible-Matrix-Compo- site Structure. Composite Structures, 570-575. http://dx.doi.org/10.1016/j.compstruct.2014.11.069
- 3. Yin, Z. and Ghoneim, H. (2014) Pumping Potential of a Flexi-ble-Matrix-Composite Structure with Negative Poisson’s Ratio. Abstracts of 1st International Conference on Mechanics of Composites, Stony Brook University, Long Island, 9-12 June 2014.
- 4. Lotfi-Gaskarimahalle, A., Scarborough III, L.H., Rahn, C.D. and Smith, E.C. (2014) Tunable Fluidic Composite Mounts for Vibration Absorber. Journal of Vibration and Control, 4, 2137-2145. http://dx.doi.org/10.1177/1077546313482340
- 5. Gureghian, R.S., Carlson, J.D., LeRoy, D.F., Marjoram, R.H., Brown, M.B. and Jolly, M.R. (1999) Controllable Platform Suspension System for Treadmill Decks and Like Devices Therefor. Patent US 5993358 A.
- 6. Kumar, N., Varela, B. and Ghoneim, H. (2015) Effective Damping of a Flexible-Matrix-Composite Laminate with a Negative Effective Poisson’s Ratio. Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, IMECE2015-50365, Houston, 13-19 November 2015. http://dx.doi.org/10.1115/imece2015-50365
- 7. Hashin, Z. (1970) Complex Moduli of Viscoelastic Composites—II Fiber Reinforced Materials. International Journal of Solids and Structures, 6, 797-807. http://dx.doi.org/10.1016/0020-7683(70)90018-1
- 8. Fukushima, K., Cai, H., Nakada, M. and Miyano, Y. (2009) Determination of Time-Temperature Shift Factor for Long-Term Life Prediction of Polymer Composites. ICCM-17, 17th International Conference on Composite Materials.
- 9. Tschoegl, N.W., Wolfgang, W.G. and Emri, I. (2002) Poisson’s Ratio in Linear Viscoelasticicty—A Critical Review. Mechanics of Time Dependent Materials, 6, 3-51. http://dx.doi.org/10.1023/A:1014411503170
- 10. Melo, J.D.D. andRadford, D.W. (2003) Viscoelastic Characterization of Transversely Isotropic Composite Laminates. Journal of Composite Mate-rials, 37.
- 11. Barbero, E.J. (2011) Intro to Composite Materials Design. CRC Press, Taylor & Francis Group.
- 12. (2007) Dynamic Mechanical Analysis Basics: Part 1 How DMA Works, Technical Note. www.perkinselmer.com
- 13. Adams, R.D. and Bacon, D.G.C. (1973) Effect of Fiber Orientation and Laminate Geometry on the Dynamic Properties of CFRP. Journal of Composite Materials, 7.
- 14. Herakovich, C.T. (1998) Mechanics of Fibrous Composites. John Wiley & Sons, Inc., 362-393.