Received 22 June 2016; accepted 16 July 2016; published 19 July 2016

ABSTRACT

A random simulation method was used for treatment of systems of Volterra integral equations of the second kind. Firstly, a linear algebra system was obtained by discretization using quadrature formula. Secondly, this algebra system was solved by using relaxed Monte Carlo method with importance sampling and numerical approximation solutions of the integral equations system were achieved. It is theoretically proved that the validity of relaxed Monte Carlo method is based on importance sampling to solve the integral equations system. Finally, some numerical examples from literatures are given to show the efficiency of the method.

Keywords:

Systems of Volterra Integral Equations, Quadrature Formula, Relaxed Monte Carlo Method, Importance Sampling

1. Introduction

In engineering, social and other areas, a lot of problems can be converted to Volterra integral equations to solve, such as elastic system in aviation, viscoelastic and electromagnetic material system and biological system, and some differential equations are often transformed into integral equations to solve in order to simplify the calculation. For example, the drying process in airflow, pipe heating, gas absorption and some other physical processes can be reduced to the Goursat problem. Then, some of the Goursat problem can be described by Volterra integral equations [1]. Another example, when one-dimensional situations are concerned and the coolant flow is incompressible, the definite solution problem of the transpiration cooling control with surface ablation appears as Volterra integral equations of second kind [2]. In practice, the analytical solutions for this kind of integral equations are difficult to obtain. Therefore, it is more practical to research the numerical method for solving this kind of integral equations.

The main aim of this paper is to propose a numerical algorithm based on Monte Carlo method for approximating solutions of the following system of Volterra integral equations

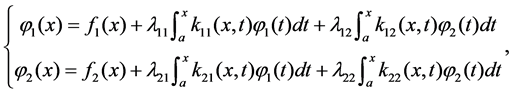(1)

where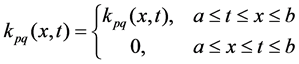, 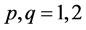are known kernel functions, the functions,

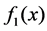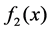are given and defined in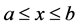, and 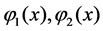are the unknown functions to be determined. One of the earliest methods for solving integral equations using Monte Carlo method was proposed by Albert [3], and was later developed [4]. Literatures [5]-[8] employed Monte Carlo method to solve numerical solutions of Fredholm integral equations of the second kind. But very few studies are devoted to employing Monte Carlo method to solve Volterra integral equations and the system of Volterra integral equations. In this paper, we present and discuss a relaxed Monte Carlo approach with importance sampling to solve numerically systems of Volterra integral equations. Due to less accuracy and lower efficiency of Monte Carlo method, in this paper, combination of Monte Carlo and quadrature formula will be used to deal with Equation (1) and importance sampling is applied to accelerate the convergence and improve the accuracy of Monte Carlo method. Some numerical examples are given to show the efficiency and the feasibility of proposed Monte Carlo method.

2. Discretizing System of Integral Equations

Here, Newton-Cotes quadrature formula is used to discretize Equation (1). Dividing the interval 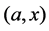into subintervals with step length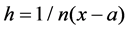, defining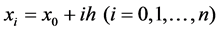, where . For convenience, denoting the notation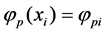, , 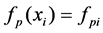, 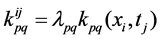where,. As,. Thus the following linear algebra system can be obtain

, (2)

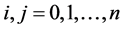where, ,

, , , is the weight of Newton-

Cotes quadrature formula. The matrix of coefficients of Equation (2) is. If we assume that there exists a unique solution of (2), the solution would be a numerical approximation of (1). This process will produce an error which is determined by numerical quadrature formula and can be reduced by increasing the number of nodes for a given quadrature formula. For a large number of nodes, Equation (2) is too large to solve directly. It is well known that Monte Carlo technique has a unique advantage for large systems or high-dimensional problems. At the same time, this method can obtain function values at some specified points or their linear combination that is just what researchers need. But for determined numerical methods, in order to obtain function value at a certain point, it is often necessary that find function values for all nodes. Here relaxed Monte Carlo method is used to Equation (2) based on a random sample from Markov chain with discrete state. According to theory of importance sampling, probability transition kernel is selected to suggest a possible move. To obtain solution of the linear algebraic system (2), the following iterative formula is considered

(3)

where is the iterative matrix, is a diagonal matrix with elements, , relaxation parameter of the iterative formula is chosen such that it minimizes the norm of for accelerating the convergence, and. The iterative formula (3) can define a Neumann series, as following

(4)

Set iterative initial value, is the exact solution of Equation (2), the truncation error and convergency of the iterative formula (3) can be obtained by the following expression

This conclusion can be proved by using theories in numerical analysis. Here, the iterative matrix satisfies

or.

To achieve a desirable norm in each row of, a set of relaxation parameters, will be used in

place of a single value. According to the arguments of Faddeev and Faddeeva [9] [10], the relaxed Monte Carlo method will converge if

,

here denotes the row norm of the given matrix.

3. Relaxed Monte Carlo Method with Importance Sampling

For Neumann series (4), we have

In order to obtain the approximation solution of linear system (2) and system of integral Equation (1), the kth iteration of will be evaluated by means of computing the following series

(5)

Construct the Markov chain

(6)

on the state space. Let the initial probability and the transition probability of Markov chain respectively

, ,

and they must satisfy and for any. According to non-after-effect

property of Markov chain, one can get

For and the mth series (5), let, estimators are established in the following form

. (7)

The weight function of Markov chain is defined as follows

(8)

By expressions (7) and (8), the following conclusion can be gotten.

Theorem 3.1 For the given, we have

. (9)

This theorem is easy to prove.

In the light of the expression (7), the following estimator is defined

(10)

and

(11)

Due to Theorem 3.1, the conclusion (11) is easy to prove.

To estimate, by the transition probability, random paths of Markov chain are simulated

the length of Markov chain is defined by, is the precision of truncation error and given in advance. Then one can evaluate the sample mean

If the standard deviation is bounded, according to the Central Limit Theorem, we would obtain

So the precision of the estimator in the sense of probability can be measured by its variance.

Based upon the minimum variance of estimator, by the variance expression

the transition probability of Markov chain should be chosen in the following form

This form of leads to that more samples are taken in regions which have higher function values. This is importance sampling.

According to the obtained approximation of global approximation functions of solutions and of Equation (1) would be achieved

(12)

4. Numerical Examples

In this section, we employ the proposed relaxed Monte Carlo method with importance sampling (say RMCIS) to compute the numerical solution of some examples and compare it with their exact solutions. The numerical results are presented in Table 1 and Table 2, where AE means absolute error for. We plot the

mean absolute errors (MAE) in Figure 1 and Figure 2. Below are the numerical results for some of them.

Example 1 Consider the equations [11] [12]

where. The exact solutions are and

. The numerical results are listed in Table 1.

Example 2 Consider the equations [13]

where. The exact solutions are and, The nu-

merical results are listed in Table 2.

5. Conclusion

In this paper, a relaxed Monte Carlo numerical method is provided to solve a system of linear Volterra integral equations. The most important advantage of this method is simplicity and easy-to-apply in programming, in comparison with other methods. The implementation of current approach RMCIS is effective. The numerical examples that have been presented in the paper and the compared results support our claims.

Funding

This research was supported by National Natural Science Foundation of China under Grant No. 11361036, Specialized Research Fund for the Doctoral Program of Higher Education under Grant No.20131514110005, Natural Science Foundation of Inner Mongolia under Grant No. 2015MS0104.

Cite this paper

Zhimin Hong,Xiangzhong Fang,Zaizai Yan,Hui Hao, (2016) On Solving a System of Volterra Integral Equations with Relaxed Monte Carlo Method. Journal of Applied Mathematics and Physics,04,1315-1320. doi: 10.4236/jamp.2016.47140

References