Received 31 March 2016; accepted 12 July 2016; published 15 July 2016

ABSTRACT

Based on the classic Lotlk-Volterra cooperation model, we establish a time-delay model of which a species cannot survive independently. By continuation theorem, we discuss existence of positive periodic solutions of the model.

Keywords:

Biological Model, Existence, Periodic Solution, Time Delay, Independent Survival

1. Introduction

The plants can survive independently and insect pollination can improve the growth rate of plants in [1] and [2]. According to this phenomenon, based on the classical Lotka-Volterra model, we establish a model of two populations of Lotka-Volterra which cannot survive independently, finally he analyzes the stability of the model.

There is still less research work of the model which cannot exist independently. The existing researches basically are the autonomous models (see [3] and [4]). In this paper, we establish a Lotka-Volterra model with time delay which a species cannot survive independently. The main aim is to discuss existence of periodic positive solution for the model.

Suppose that there are two plant populations (A and B) living in their natural environment, which are free from other interference factor. Let 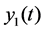and 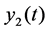are the population density of plant A and plant B,

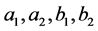are continuous functions with periodic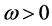, and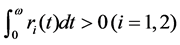. The constants

are stimulations of living environment. By the thought of [1]-[4], we could have got the following Lotka-Volterra model with time delay which a species cannot survive independently.

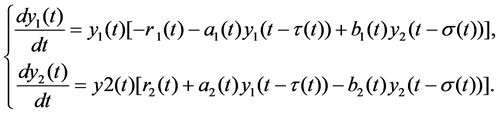(1)

The main aim of the paper is to discuss existence of periodic positive solution for the model.

2. Lemma 1 and Lemma 2

Assume X and Z are normed vector space, 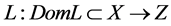and 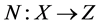are linear mappings. If L is Fredholm mapping which Zero is index, and there are continuous projection 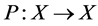and, such that 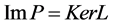and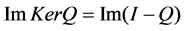, we can get that is reversible. If Inverse mapping 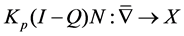is tight, we call N is tight on.

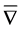Lemma 1 (Continuation theorem) [5] Let L be the mapping of Fredholm with zero index, collection N is tight on collection. Suppose the following: for any, the solution of equation; for any and. Then, there is at least a solution for on.

Lemma 2 is positive invariant set of model (1).

Proof: By formula (2), we have

(2)

Since formula (2) is always true for, lemma 2 is proved.

For the convenience of discuss, we give following notations.

, ,

, , ,.

3. Existence of Periodic Solutions

In order to apply Continuation theorem to system (3), we define

and

,

then X, Z is Banach space under the norm (see [6] and [7]).

Let, , the Equation (1) can be turns into

(3)

Since is periodic, we know that

and

are continuous function with the periodicity.

Let, , , for, , for, then, is closed set in set Z,

, and P, QP and Q is the continuous projection, such that,. Thus there is the inverse mapping of L and

.

So that we get

,

It is obvious that and is continuous.

We assume that is bounded open set. It is obvious that is bounded. We have that is compact set by Arzela-Ascoli theorem, so we get N is L-tight on.

The corresponding operator equation is with，we have the following formula

(4)

We assume that is the solution for system (4) with，by integral we get the following formula (5)

(5)

To move term from one side of an algebraic equation to the other side, reversing its sign to maintain equality, we get the following

(6)

(7)

From formula (5), formula (6) and formula (7), we have

(8)

and

(9)

From formula (8) and formula (9) we can get

(10)

(11)

From formula (10) and formula (11) we get

So that

Similarly, we have

Using formula (7) we get

Thus

(12)

Similarly, we have

(13)

From formula (8) and formula (13) we get

From formula (9) and formula (12) we get

Since, it exists, such that

(14)

By formula (12), formula (13) and formula (14), we get

,

,.

So that

,.

It is obvious that has nothing with choose of. Thus the following formula (15) has a unique positive solution.

(15)

Let, where is sufficiently large and

. Then, , then satisfying the first

condition for Lemma 1. When,

So that, satisfying all the conditions for Lemma 1. We have that there is at least a solution with on from Lemma 1.

Let, , when, is positive periodic solution for system (1) which the length of. Hence, there is at least a positive periodic solution for system (1).

Theorem If, then is a positive periodic solution for system (1). In other word, there is at least one positive periodic solution for system (1).

Acknowledgements

This research was financially supported by the National Science Foundation of Zhejiang Province (LY12A01010) and by the College Students’ Scientific and Technological Innovation of Zhejiang Province (2015R411035).

Cite this paper

Binbin Wang,Hailiang Zhang, (2016) Existence of Positive Periodic Solutions for a Time-Delay Biological Model. Journal of Applied Mathematics and Physics,04,1300-1304. doi: 10.4236/jamp.2016.47137

References

NOTES

^*Corresponding author.