Received 24 May 2016; accepted 12 July 2016; published 15 July 2016

ABSTRACT

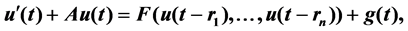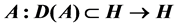In this paper, we consider an abstract non-autonomous evolution equation with multiple delays in a Hilbert space H: where is a positive definite selfadjoint operator, is a nonlinear mapping, 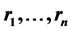are nonnegative constants, and 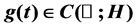is bounded. Motivated by [1] [2], we obtain the existence and stability of synchronizing solution under some convergence condition. By this result, we provide a general approach for guaranteeing the existence and stability of periodic, quasiperiodic or almost periodic solution of the equation.

Keywords:

Pullback Attractor, Cocycle System, Stability, Synchronizing Solution

1. Introduction

In this paper, we consider the following non-autonomous evolution equation with multiple delays in a Hilbert space H:

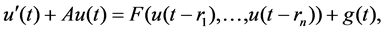(1.1)

where is a positive definite selfadjoint operator with compact resolvent, is a nonlinear mapping, 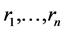are nonnegative constants, and 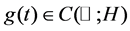is bounded.

This partial differential equations with delays (1.1) has extensive physical background and realistic mathematical model, hence it has been considerably developed and the numerous properties of their solutions have been studied, see [3]-[5] and references therein. Ref. [4] and [5] mainly discussed the existence and stability of periodic solutions of (1.1). Ref. [3] is concerned with the existence of locally almost periodic solutions of (1.1) by pullback attractor theory.

In this paper, our aim is to study the existence and stability of synchronizing solution of Equation (1.1). Motivated by [1] [2], we obtain the existence and stability of synchronizing solution under some convergence condition. The result be of most interest when we choose 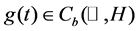be translation compact (resp. recurrent or almost periodic or quasiperiodic or periosdic), then we can obtain the synchronizing solution of Equation (1.1) is also translation compact (resp. recurrent or almost periodic or quasiperiodic or periosdic). This result provides a general approach for guaranteeing the existence and stability of periodic, quasiperiodic, almost periodic or recurrent solution of the equation.

The rest of the paper is organized as follows. In Section 2, we provide some preliminaries. In Section 3, we establish the existence and stability of synchronizing solutions under some convergence condition.

2. Preliminaries

This section consists of some preliminary work.

2.1. Analytic Semigroups

Let H be a Hilbert space with the inner product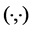. We will use to denote the norm of H and use to denote the norm of bounded linear operators on H. Let

be a positive definite selfadjoint operator with compact resolvent, and let

Be the eigenvalues of A (counting with multiplicity) with the corresponding eigenvectors which form a canonical basis of H.

For, define the powers as follows:

Let

Then, is a Hilbert space with the inner product and norm defined as

respectively. We also know that for any, the embedding is compact; moreover, it holds that

(2.1)

2.2. Pullback Attractors

We recall some basic definitions and facts in the theory of non-autonomous dynamical systems for skew-product flows on complete metric spaces.

Let be a complete metric space, be a metric space which will be called the base space (or symbol space). is a mapping, form a group, that is, satisfies

1);

2).

Definition 2.1 A mapping is said to be a continuous cocycle on X with respect to group, if

1);

2) and;

3) is continuous.

The mapping defined by

forms a semigroup on and is called a skew-product flow.

Definition 2.2 A family of nonempty compact sets of X is called a global pullback attractor of the cocycle if it is -invariant, that is,

and pullback attracting, that is, for any bounded subset B of X,

and is the minimal family of compact sets that is both invariant and pullback attracting.

2.3. Global Pullback Attractor of (1.1)

We present essential conditions on the nonlinearity F to guarantee the dissipation and the existence of pullback attractor of (1.1).

We first discuss the well-posedness of the initial value problem of the equation.

Let, where. is endowed with the norm

For and, we define by

Consider the initial value problem of the evolution equation with delays

(2.2)

where is continuous and there exist positive constants and such that F satisfies the following conditions:

(H1) For all and

(H2)

(H3) For any and bounded interval J, there exists such that

for all and, where (and hereafter) denotes the ball in centered at 0 with radius R;

and is bounded, that is, there exists a positive constant such that for all

Theorem 2.3 Assume that and F satisfies (H1)-(H3). Then, the problem (2.2) has a unique global mild solution which depends on continuously, and

Proof. The proof can be obtained by Theorem 5 in [3].

Remark 2.4 satisfies the following integral equation:

. (2.3)

Let the space be equipped with the compact-open topology:

It is well known that this topology is metrizable and is a complete metric space.

Give is bounded, we define the base space as

So the shift operator defined for each by

,

forms a continuous dynamical system on the base space.

Define as follows:

where is the unique solution of the problem (2.2) with. Then is a cocycle system on with the base space and driving system.

Since Theorem 12 in [3], we have the following existence result concerning the pullback attractors.

Theorem 2.5 Let. If F satisfies conditions (H1)-(H3), then has a unique global pullback attractor.

3. Synchronizing Solutions

In this section, we establish some results on synchronizing solutions for (1.1), by developing some techniques inspired by works [2] and [1]. It is known that if g has some special structure, i.e., periodic, quasiperiodic, almost periodic etc., then we can obtain a compact base space with same structure. Combined with the theory of uniform pullback attractors for dynamical systems in [6], we will prove that under some convergence condition, Equation (1.1) have some entire solution that synchronize with the motion of the driving system. We call synchronizing solutions for (1.1).

Now, we consider that is translation compact, then the base space is compact.

If furthermore, the Lipschitz coefficients of F in the set satisfy:

, (H4)

then we have the following results about synchronizing solutions for (1.1).

Theorem 3.1 Assume, and F satisfies (H1)-(H4). Let is translation compact in. Then:

1) There exists a such that for each, is the unique bounded entire solution of (1.1) on;

2) For any, there exists a unique solution of (1.1) on with initial value that satisfies

Proof. By Theorem 2.5, we have proved that the cocycle mapping has a pullback attractor, and we know that is bounded. So is given as the union all bounded entire solution.

As Definition 2.2, it is -invariant, that is,

One can also write the non-autonomous invariance property as

(3.1)

In what follows we show that for each, is in fact a singleton, i.e.,

for some.

Let. By invariance property (3.1), for any there exist such that

We know that

where is the solution of (2.2) with initial value, and

where is the solution of (2.2) with initial value.

Let, we have

Taking inner product with and using Hӧlder’s inequality, , Poincáre’s inequality and Young’s inequality, we have

(3.2)

which yields that

(3.3)

where. Integrating from 0 to t, we obtain

(3.4)

where.

Let. We obain

(3.5)

Since and (H4), we have. Then by Gronwall’s lemma we have

(3.6)

Then, we can obtain that

(3.7)

which implies as Hence,.

Now define as

We infer from Corollary 2.8 in [6] that is upper semi-continuous in. This reduces to the continuity of in when the are single point sets. Hence, is continuous. For each, set

By invariance property of one trivially checks that is precisely the unique solution of (1.1) on. Since Theorem 4.3 in [5], is a uniform pullback attractor. That is, for any, we have

where denotes the semi-Hausdorff distance in. Then, it is uniformly forwards attracting,

Thus we can deduce that

The proof is complete.

Corollary 3.2 Let is periodic (resp. quasiperiodic, almost periodic, recurrent), then under con- ditions of Theorem 3.1 the non-autonomous Equation (1.1) admits a unique periodic (resp. quasiperiodic, almost periodic, recurrent) solution and every other solution of this equation are asymptotically periodic (resp. asymptotically quasiperiodic, asymptotically almost periodic, asymptotically recurrent).

Proof. Let be a function from Theorem 3.1, then according to this theorem we conclude that is the unique bounded solution of (1.1) synchronizing with the motion of the driving system. In particular, if is periodic (resp. quasiperiodic, almost periodic, recurrent), then so is By (2) of Theorem 3.1, we know that every other solution of this equation is asymptotically periodic (resp. asymptotically quasiperiodic, asymptotically almost periodic, asymptotically recurrent). The proof is complete.

Acknowledgements

This work was supported by NNSF (11261027), NNSF (11161026) and the Research Funds of Lanzhou City University (LZCU-BS2015-01).

Cite this paper

Jinying Wei,Yongjun Li,Xiaohua Zhuo, (2016) The Existence and Stability of Synchronizing Solution of Non-Autonomous Equations with Multiple Delays. Journal of Applied Mathematics and Physics,04,1294-1299. doi: 10.4236/jamp.2016.47136

References