Open Access Library Journal
Vol.02 No.12(2015), Article ID:68915,9 pages
10.4236/oalib.1102131
Numerical Analysis of the Effect of Temperature and External Optical Feedback Variation on the Output Characteristics of External Cavity Semiconductor Laser Based Fiber Bragg Gratings
Hisham K. Hisham
Department of Electrical Engineering, Faculty of Engineering, Basra University, Basra, Iraq

Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 November 2015; accepted 3 December 2015; published 8 December 2015
ABSTRACT
The temperature and external optical feedback (OFB) effects on power characteristics of external cavity semiconductor laser model based fiber Bragg gratings (FBGs) are numerically analyzed. In this model, fiber Bragg grating (FBG) is used as a wavelength selective element to control the properties of the laser output by controlling the external OFB level. The study is performed by modifying output laser equations that are solved by considering the effects of ambient temperature (T) variations and external OFB. In this study, the temperature dependence (TD) of laser characteristics is calculated according to TD of laser parameters instead of using the well-known Pankove relationship. Results show that by increasing the external OFB level, the laser output power improves significantly. Also, results show that by changing the operating temperature 15˚C (from 15˚C to 30˚C), there is no great impact on the output characteristics. The obtained results can provide an important idea for the practical fabrication for this type of lasers.
Keywords:
External Cavity Semiconductor Lasers, External Optical Feedback, Fiber Bragg Gratings
Subject Areas: Electric Engineering

1. Introduction
With a rapid increase in demand for large optical transmission capacity, wavelength-division multiplexing (WDM) systems have become essential as a huge and high-speed data transmission method. Thus far, WDM systems up to 50-GHz channel spacing have already been used [1] - [7] . However, in the near future, much larger transmission capacity would be required with further progress of information technology revolution. To satisfy this requirement, dense WDM (DWDM) systems with narrower channel spacing will be indispensable [3] . In WDM systems, coherent light source with a more accurate and more stable lasing wavelength is required [4] . Distributed feedback (DFB) semiconductor laser diodes are widely used in these systems as single-mode laser sources. However, tuned DFB lasers are expensive because of the relative bad yield rate. Since the emission wavelength of a DFB laser depends heavily on temperature and injection current [5] - [7] , it is difficult to sort out DFB laser modules, which are tuned at predetermined wavelength. In addition, the improvements in the laser manufacture allow today operating un-cooled directly modulated lasers over abroad temperature range. Since a significant reduction in the optical system can be achieved without the need to control the temperature of the laser. Un-cooled directly modulated laser has been regarded as one of the key technologies for optical networks in the future.
On the other hand, the semiconductor laser diodes (SLDs) are extremely sensitive to external optical feedback (OFB), which arises in practical applications due to back reflections depending on the feedback level [8] . In contrast, much cheaper Fabry-Perot laser diodes (FP-LDs) are not very stable and spectrally not narrow. Their multi-mode operation and strong dependence on temperature and supply current [5] make them not too effective for using as relatively stable sources in the WDM applications. One way of improving the mode selectivity is to make the feedback frequency-dependent, so that the cavity loss is different for different longitudinal modes [9] - [13] .
In external cavity semiconductor laser based fiber Bragg gratings (ECSL-FBGs), the emission wavelength is dependent only on Bragg wavelength and independent of chip temperature or injection current. Precise adjustment of the Bragg wavelength of a fiber grating (FG) is available compared with the emission wavelength of DFB lasers. So the lasing wavelength in ECSL-FBGs model is highly stable with temperature and current. In addition, the Bragg wavelength can be controlled more precisely than that of the DFB lasers in the actual fabrication process. As a result, the ECSL-FBGs model realizes much better wavelength stability and controllability [14] - [20] . Therefore, ECSL-FBGs model is promising as a high stable and low-cost light source of a future DWDM system compare with other laser models.
To date, many experimental and theoretical studies have been reported on the FGFP laser [1] [4] [21] . However, in most of these studies, the temperature effect is not taken into account. In addition, they assumed that the external cavity diode laser was under strong OFB; i.e. the effect of external OFB was not investigated in weak and moderate levels. Thus, full visualizations of the temperature and the external OFB effects on the output characteristics were not provided. Therefore, an accurate knowledge on the effects of these parameters is very important for avoiding ECSL-FBGs to operate in inoperable regime.
The paper is structured as follows: The external cavity semiconductor laser model based fiber a Bragg grating (ECSL-FBGs) is given in the next section. Section 3 presents the temperature dependence for ECSL-FBGs model output power with external OFB. The simulation results are discussed in Section 4 followed by the conclusion.
2. External Cavity Semiconductor Laser Model Based Fiber Bragg Gratings
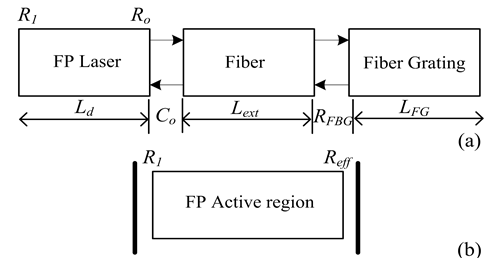
The external cavity semiconductor laser model based fiber Bragg gratings (ECSL-FBGs) consists of three main sections as shown in Figure 1(a). The first section is the Fabry-Perot laser diode (FP-LD) of length Ld. It is assumed that the reflectivity of the chip front facet (Ro) is very low to suppress FP mode oscillation and to stabilize the external cavity mode, while the rear facet has high reflectivity (R1). The second section is a fiber of length Lext; and the third is the FBGs with reflection coefficient of rFBG. The FP-LD and the FBGs are optically coupled through a coupling lens, and thus external cavity is constructed. The temperature dependence (TD) to the photons round-trip time inside the internal and the external cavity are τd(T) = 2nd(T)Ld/c and τe(T) = 2Lextnext(T)/c, respectively, where c, is the velocity of the light in the vacuum, nd(T) is the TD group refractive index of the FP-LD, and next(T) is the TD fiber refractive index.
This configuration may be conveniently analyzed as a simple two-mirror laser structure (Figure 1(b)) by replacing the FP diode laser output facet reflectivity Ro by a complex-valued effective reflection coefficient Ref [14] .
Figure 1. (a) Schematic structure of FGFP laser; (b) Simplified configuration [14] .
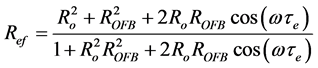 (1)
(1)
where 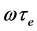 is the phase of the reflected light that travels through the external cavity and
is the phase of the reflected light that travels through the external cavity and  is the laser angular frequency. In Equation (1),
is the laser angular frequency. In Equation (1), 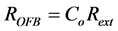 is the amount of OFB reflection coupled into FP-LD, where
is the amount of OFB reflection coupled into FP-LD, where 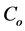 is the amplitude coupling coefficient between the FP-LD and the fiber grating (FG), and
is the amplitude coupling coefficient between the FP-LD and the fiber grating (FG), and 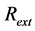 is the power reflectivity of FG defined as [21] [22]
is the power reflectivity of FG defined as [21] [22]
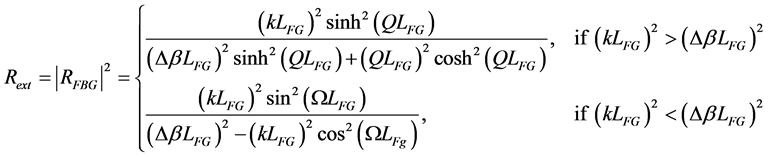 (2)
(2)
where 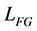 is the grating length,
is the grating length, 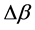 is the wavelength detuning, k is the coupling strength,
is the wavelength detuning, k is the coupling strength, 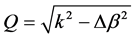 ,
,
and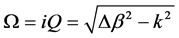 . The phase coefficient for reflection light
. The phase coefficient for reflection light 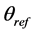 is derived from the differential equations in [22] and is given by
is derived from the differential equations in [22] and is given by
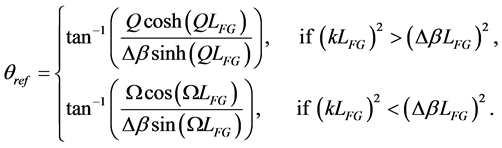 (3)
(3)
By considering the phase change introduced by the optical filter in Equation (1), 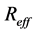
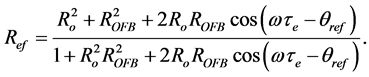
3. Output Characteristics of ECSL-FBGs Laser Model
The temperature dependence (TD) of threshold current Ith,fe(T) of ECSL-FBGs laser under the effect of external OFB can be written as [11] [13]
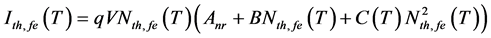
where q is the electron charge, V is the FP-LD active region volume, Anr describes the non-radiative recombination rate due to traps or surface states, C(T) is the TD Auger process, B is the radiaitive recombination coefficient, and Nth,fe(T) is the TD carrier density at the threshold condition. The Nth,fe(T) can be represented by modifying the well-known expression in [13] as
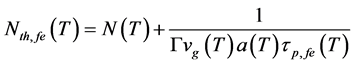
where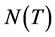
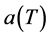
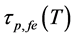
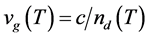
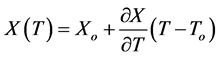
where Xo is the initial value found at the reference temperature (To), which is considered at the room temperature (25˚C). Since the external OFB only affects on the photon lifetime in Equation (6), 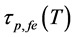
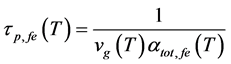
where 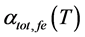
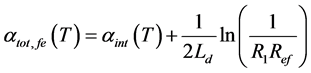
where 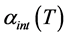
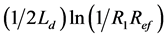
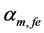
under the effect of external OFB. Based on Equations (1)-(9), the TD threshold carrier density 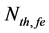
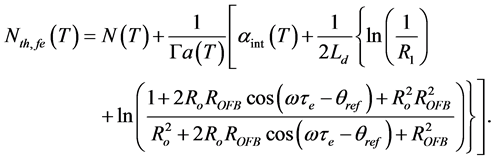
Equation (10) gives a general expression for the TD threshold carrier density under the effect of external OFB, which is used to calculate the net rate of stimulated emission in the ECSL-FBGs laser active region. Finally, the TD of the output power from the front face of ECSL-FBGs laser model under the effect of the external OFB corresponding to the selected Bragg wavelength can be written as
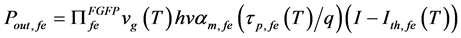
where
4. Simulation Analysis
In this study, the output characteristics of ECSL model with uniform FBGs operating at 1550 nm wavelength is analyzed. The parameters of the model used in the analysis are shown in Table 1. All these values are fixed throughout this study, except otherwise is stated.
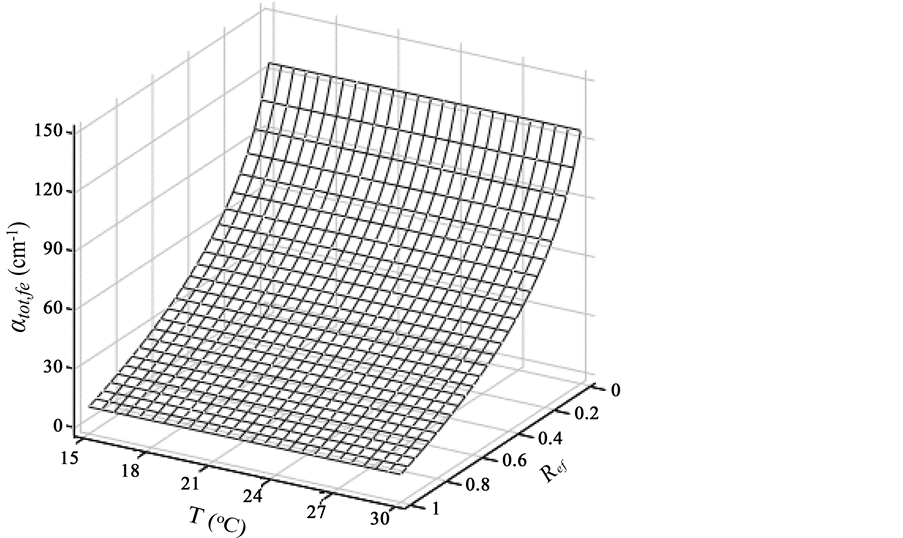
Figure 2 shows the effect of temperature (T) and effective reflectivity (Ref) variations on the total cavity loss (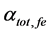
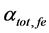
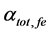
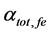
Table 1. Parameters of FGFP at reference temperature To (To = 25˚C) [14] - [20] .
Figure 2. Effect of temperature variations and effective reflectivity on total cavity loss of ECSL-FBGs laser model.
Figure 3 show the effect of temperature (T) and effective reflectivity (Ref) variations on ECSL-FBGs laser photon lifetime (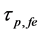
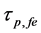
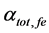
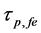
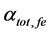
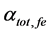
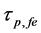
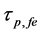
The effect of temperature (T) and effective reflectivity (Ref) variations on threshold carrier density (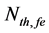
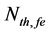
Figure 3. Effect of temperature (T) and effective reflectivity (Ref) variations on ECSL-FBGs laser photon lifetime.
Figure 4. Effect of temperature (T) and effective reflectivity (Ref) variations on ECSL-FBGs laser threshold carrier density.
OFB mirror loss, as well as by the TD of 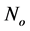
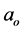
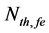
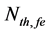
Figure 5 shows the dependence of ECSL-FBGs laser threshold current (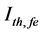
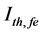
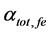
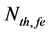
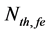
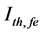
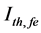
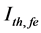
Figure 5. Effect of temperature variations and effective reflectivity (Ref) on ECSL-FBGs laser threshold current.
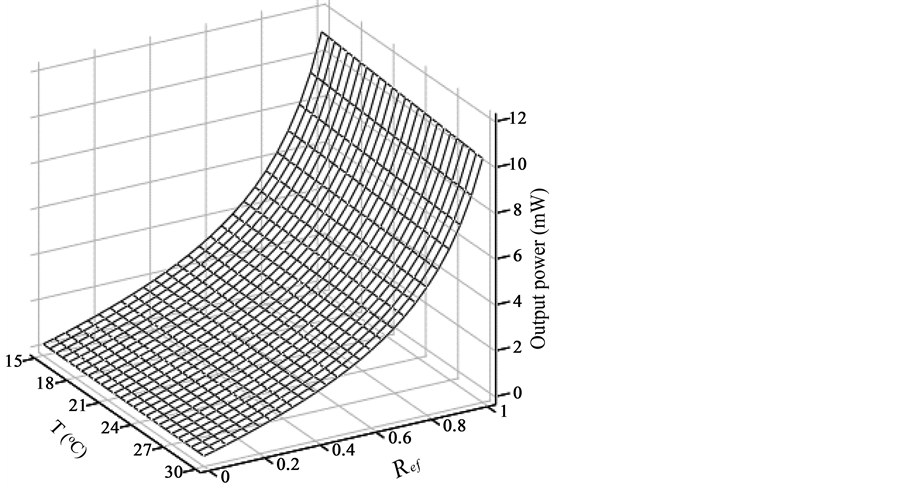
Figure 6. Effect of the temperature (T) and the effective reflectivity (Ref) variations on ECSL-FBGs laser output power.
for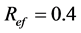
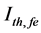
Finally, Figure 6 shows the effect of the temperature variations and the effective reflectivity (Ref) on ECSL- FBGs laser output power. The ECSL-FBGs laser model with threshold current (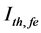
5. Conclusion
A numerical study on the effect of the temperature (T) variations and external OFB on output characteristics of ECSL-FBGs laser model is successfully conducted. It has been shown that, through simulation, the output characteristic of ECSL-FBGs laser model is extremely sensitive to the external OFB level. On the other hand, results show that there is no effected effect for temperature variation on the model output. This is because, in this study, the temperature dependence (TD) of laser characteristics is calculated according to TD of laser parameters instead of using the well-known Pankove relationship [4] [14] - [20] . In this case, we have taken into account the thermal effect of each affecting parameter on the model instead of using an empirical equation for temperature analysis. Thus, by this way the simulation results are more accurate than previous cases.
Cite this paper
Hisham K. Hisham, (2015) Numerical Analysis of the Effect of Temperature and External Optical Feedback Variation on the Output Characteristics of External Cavity Semiconductor Laser Based Fiber Bragg Gratings. Open Access Library Journal,02,1-9. doi: 10.4236/oalib.1102131
References
- 1. Hashimoto, J.I., Takagi, T., Kato, T., Sasaki, G., Shigehara, M., Murashima, K., Shiozaki, M. and Iwashima, T. (2003) Fiber-Bragg-Grating External Cavity Semiconductor Laser (FGL) Module for DWDM Transmission. Journal of Light-wave Technology, 21, 2002-2009.
http://dx.doi.org/10.1109/JLT.2003.815498 - 2. Bhatt, S. and Jhaveri, S. (2013) A Review of Dense Wavelength Division Multiplexing and Next Generation Optical Internet. International Journal of Engineering Science and Innovative Technology, 2, 404-412.
- 3. Tripathi, D.K., Singh, P., Shukla, N.K. and Dixit, H.K. (2014) Design and Performance Study of Triple-Band DWDM (160 Channel). International Journal of Applied Control, Electrical and Electronics Engineering, 2, 45-51.
- 4. Hisham, H.K., Abas, A.F., Mahdiraji, G.A., Mahdi, M.A. and Mahamd Adikan, F.R. (2014) Linewidth Optimization in Fiber Grating Fabry-Perot Laser. Optical Engineering, 53, 1-8.
http://dx.doi.org/10.1117/1.OE.53.2.026107 - 5. Timofeev, F.N., Simin, G.S., Shatalov, M.S., Bayvel, P., Wyatt, R., Lealman, I., Kashyap, R. and Gurevich, S.A. (2000) Experimental and Theoretical Study of High Temperature-Stability and Low-Chirp 1.55 μm Semiconductor Laser with an External Fiber Grating. Journal of Fiber and Integrated Optics, 19, 327-353.
http://dx.doi.org/10.1080/014680300300001699 - 6. Anees, S.B., Shah, S.K. and Ali, A. (2014) Next Gen. Dense Wavelength Division Multiplexing. International Journal of Advanced Research in Computer Science and Software Engineering, 4, 1000-1008.
- 7. Bharath, K.S. and Jayaraj, N. (2014) Network Planning and Engineering for Fiber Optic Transport Systems. International Journal of Innovative Research in Computer and Communication Engineering, 2, 4296-4301.
- 8. Kapusta, E.W., Luerben, D. and Hudgings, J.A. (2006) Quantifying Optical Feedback into Semiconductor Laser via Thermal Profiling. IEEE Photonics Technology Letters, 18, 310-312.
http://dx.doi.org/10.1109/LPT.2005.861967 - 9. Othonos, A. and Kalli, K. (1999) Fiber Bragg Gratings: Fundamentals and Applications in Telecommunications and Sensing. Artech House, Inc.
- 10. Yu, H.G., Wang, Y., Xu, C.Q., Wojcik, J. and Mascher, P. (2005) Spectral Investigation of Multimode Fiber Bragg Grating Based External Cavity Semiconductor Lasers. IEEE Journal of Quantum Electronics, 41, 1492-1500.
http://dx.doi.org/10.1109/JQE.2005.857706 - 11. Agrawal, G.P. and Dutta, N.K. (1986) Long-Wavelength Semiconductor Lasers. John Wiley & Sons, New York.
http://dx.doi.org/10.1007/978-94-011-6994-3 - 12. Osmundsen, J.H. and Gade, N. (1985) Influence of Optical Feedback on Laser Frequency Spectrum and Threshold Conditions. IEEE Journal of Quantum Electronics, 19, 465-469.
- 13. Ming, M. and Liu, K. (1996) Principles and Applications of Optical Communication. The McGraw-Hill, New York.
- 14. Hisham, H.K., Abas, A.F., Mahdiraji, G.A., Mahdi, M.A. and Muhammad Noor, A.S. (2012) Relative Intensity Noise Reduction by Optimizing Fiber Grating Fabry-Perot Laser Parameters. IEEE Journal of Quantum Electronics, 48, 385-393.
http://dx.doi.org/10.1109/JQE.2011.2181489 - 15. Hisham, H.K., Abas, A.F., Mahdiraji, G.A., Mahdi, M.A. and Muhammad Noor, A.S. (2012) Characterization of the Small-Signal Intensity Modulation for Single-Mode Fiber Grating Fabry-Perot Lasers. OPT Review, 19, 64-70.
http://dx.doi.org/10.1007/s10043-012-0014-x - 16. Hisham, H.K., Abas, A.F., Mahdiraji, G.A., Mahdi, M.A. and Muhammad Noor, A.S. (2012) Characterization of Phase Noise in a Single-Mode Fiber Grating Fabry-Perot Laser. Journal of Modern Optics, 59, 393-401.
http://dx.doi.org/10.1080/09500340.2011.629060 - 17. Hisham, H.K., Mahdiraji, G.A., Abas, A.F., Mahdi, M.A. and Mahamd Adikan, F.R. (2012) Characterization of Turn-On Time Delay in a Fiber Grating Fabry-Perot Lasers. IEEE Photonics Journal, 4, 1662-1678.
http://dx.doi.org/10.1109/JPHOT.2012.2214207 - 18. Hisham, H.K., Mahdiraji, G.A., Abas, A.F., Mahdi, M.A. and Mahamd Adikan, F.R. (2012) Characterization of Transient Response in Fiber Grating Fabry-Perot Lasers. IEEE Photonics Journal, in Press.
- 19. Hisham, H.K., Abas, A.F., Mahdiraji, G.A., Mahdi, M.A. and Mahamd Adikan, F.R. (2013) Linewidth Characteristics of Un-Cooled Fiber Grating Fabry-Perot Laser Controlled by the External Optical Feedback. Optik, 124, 1763-1766.
http://dx.doi.org/10.1016/j.ijleo.2012.05.004 - 20. Hisham, H.K., Abas, A.F., Mahdiraji, G.A., Mahdi, M.A. and Mahamd Adikan, F.R. (2012) Improving the Characteristics of the Modulation Response for Fiber Grating Fabry-Perot Lasers by Optimizing Model Parameters. Optics & Laser Technology, 44, 1698-1705.
http://dx.doi.org/10.1016/j.optlastec.2012.01.027 - 21. Kallimani, K. and Mahony, J.O. (1998) Calculation of Optical Power Emitted from a Fiber Grating Laser. IEE Proceedings—Optoelectronics, 145, 319-324.
http://dx.doi.org/10.1049/ip-opt:19982464 - 22. Othonos, A. and Kalli, K. (1999) Fiber Bragg Grating: Fundamentals and Applications in Telecommunications and Sensing. Artech House, Boston.
- 23. Timofeev, F.N., Simin, G., Shatalov, M., Gurevich, S., Bayvel, P., Wyatt, R., Lealman, I. and Kashyap, R. (2000) Experimental and Theoretical Study of High Temperature-Stability and Low-Chirp 1.55 Micron Semiconductor Laser with an External Fiber Grating. Fiber and Integrated Optics, 19, 327-354.
http://dx.doi.org/10.1080/014680300300001699