Received 10 March 2016; accepted 12 July 2016; published 15 July 2016

ABSTRACT

The paper proves the convergence theorem of set-valued Superpramart in the sense of weak convergence under the X^* separable condition. Using support function and results about real-valued Superpramart, we give the Riesz decomposition of set-valued Superpramart.

Keywords:

Set-Valued, Superpramart, Weak Convergence, Riesz Decomposition

1. Introduction

Reference [1] gives Riesz decomposition of set-valued supermartingale in real space and promotes the results to reflexive Banach spaces (reference [2]). Reference [2] gives the counter-example that not all of the set-valued martingale has Riesz decomposition in a two-dimensional plane case. The fundamental reason is the defects of algebraic operation on hyperspace. Therefore, the research can pursue the unstrict sense of Riesz decomposition instead of studying various sense of Riesz decomposition. Reference [2] shows the other Riesz decomposition of set-valued supermartingale in real space. Reference [3] gives Riesz decomposition of set-valued supermartingale in the general Banach space under the X^* separable condition. References [4] and [5] research Riesz decomposition of set-valued submartingale in the general Banach space. Reference [6] studies Riesz decomposition in weak set-valued Amart. Reference [7]-[9] gives every sense of Riesz decomposition of set-valued Pramart in the general Banach space under the X^* separable condition. Reference [10] studies the problems of Riesz decomposition of set-valued Pramart. All of the above studies have given the necessary and sufficient conditions for Riesz decomposition. The research of every sense of Riesz decomposition of set-valued Superpramart is still rare.

The paper firstly demonstrates convergence theorem that set-valued Superpramart is in the sense of weak convergence under the X^* separable condition. On this basis, using support function and results about real- valued Superpramart, we give a class of Riesz decomposition of set-valued Superpramart.

2. Method

Assume (X,‖・‖) as a separable Banach space, D₁ is X-fan subset of the columns that can be condensed. X^* is the dual space X. X^* is separable. D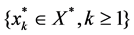^* = is X^*-fan subset of the columns that can be condensed, remember

Any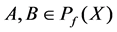, define

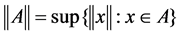
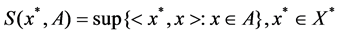
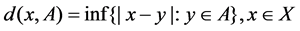
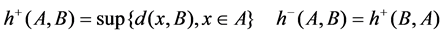
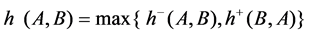
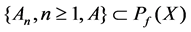If for any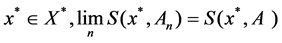, we call A_n weak convergence in A, denote as

, or.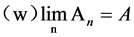

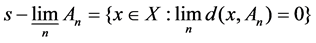
If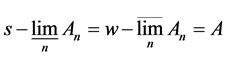, then we call 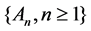Kuratowski-Mosco significance of convergence in A, denote as (K-M), or.

Assume (W,G,P) is a complete probability space. {G_n, n ≥ 1} is the G’s rise, and G = ÚG_n, indicates stop (bounded stopping),., said the set value is mapped to a random set (or on G measurable). If for any open set G, it has. We define {F_n, G_n, n ≥1}

as adapted random set columns. If, F_n can be measured by G_n. If, F is bounded integrable. represents that the value of is all the integrable bounded random set.

In order to write simply, often eliminating the almost certainly established under the meaning of the equations, inequalities and tag contain relations sense “a.s.”, {F_n, G_n, n ≥ 1}. {x_n, G_n, n ≥ 1} is often referred as, {x_n, n ≥ 1}.

Definition 1 Supposing is a real-valued integrable adapted column

1) If, call as Subpramart.

2) If, call as Superpramart.

Definition 2 Supposing is a valued adapted random set column

If, call as set-valued Superpramart.

Definition 3 Supposing we call A and B are homothetic, if exists, then it has A = B + C.

Definition 4 We call set-valued Superpramart has Riesz decomposition, if set-valued martingale and set-valued Superpramart exist, lets

.

Lemma 1 [11] If is set-valued Superpramart, then

1), is real-valued Superpramart.

2), is real-valued Subpramart.

Lemma 2 Supposing is real-valued Superpramart and, then exist and is integrable.

Proof: is the real-valued Subpramart, and reference [12] theorem 5 (corollary 1) is known.

Lemma 3 [7] Supposing, if

1);

2) are limited existing, if it has let.

Lemma 4 Supposing is set-valued Superpramart and, then it has ran-

dom set, let.

Proof:, we know is a real-valued Superpramart from reference [11] theorem 3.1,

and because, we know exists and is limited from refer-

ence [12] theorem 5, and through the list of D^*, we know exists and is limited in little-known set of N, , , by the maximum inequality and Lemma 3, the existence of F lets , then by reference [2] corollary 2.1.1 and theorem 2.1.19, we know F is a random set, the conclusion is proved.

Lemma 5 Supposing is a real-valued Superpramart, and, then it has an unique fac-

torization, where is a real-valued martingale, is a real-valued Superpramart, and.

Proof: From Lemma 2, we know, noting, it’s easy to find taht is a real-valued martingale, making, it’s easy to know is a real-valued Superpramart,

and, it also has.

The uniqueness is proved by the following: Supposing, so , because (i = 1, 2) is a real-valued martingale, is a real-valued martingale from the above equation, then

, (from reference [12] theorem 7), so

, the uniqueness is proved.

Lemma 6 Supposing is a set-valued Superpramart, and, if , then.

Proof: From Lemma 4, we know the random set exists, then it has, and

noting, from reference [11] theorem 3.1, we know is a real-valued

consistent Subpramart, then from reference [2] Lemma 4.4.2, we know the little-known set N exists,

, , From inequality

and the usual density method, we known, , it indicates, then.

Lemma 7 Supposing is a set-valued Superpramart, and, the followings are equivalent:

1) can be the Riesz decomposition.

2), F_n and E(F|G_n)(n ≥ 1) are homothetic, where

Proof: We prove firstly, because, it’s easy to know

, by the lemma Fatou, we know

, then.

1) 2) because, ,

Then, S(x^*,F_n) = S(x^*,G_n) + S(x^*,Z_n).

From Lemma 1, Lemma 6 and reference [2] lemma 4.1.3, it’s easy to know the above equation is the Riesz decomposition of real-valued Superpramart, and from Lemma 5 and its proof process, we notice and know, by the separability of X^* and the continuity of X^* support function, we know from reference [2] corollary 1.4.1 that:, namely, F_n and E(F|G_n) are homothetic.

2) 1) Noting E(F|G_n), it’s easy to know {G_n, n ≥ 1} is the value martingale of, and

, making, the following is the proof that is the value Super-

pramart of, because

S(x^*,F_n) = S(x^*,G_n) + S(x^*,Z_n)

S(x^*,Z_n) = S(x^*,F_n) – S(x^*,G_n)

It’s easy to prove, so.

E(F_t|G_s) = G_s + E(Z_t|G_s), sÎT, tÎT (s), from reference [2] lemma 5.3.6, we know

Then, we know is set-valued Superpramart the proof is set below, because

S(x_i^*,Z_n) = S(x_i^*,F_n) – S(x_i^*,G_n), x^*_iÎD^*

=S(x_i^*,F_n) – S(x_i^*,E(F|G_n))

=S(x_i^*,F_n) – E(S (x_i^*,F)|G_n), and from the list of D^*, we know the little-known set N₁, and, , , using Lemma 3, we know,

Noting, from reference [11] lemma 3.2, we know is a real-valued

consistent Subpramart, and from reference [2] lemma 4.4.2, we know the little-known set N₂ exists,

, , from inequality

and the usual density method, we know, , then from reference [2] lemma 4.5.4,.

3. Conclusion

The paper proves the convergence theorem of Superpramart in the sense of weak convergence. And on the basis of this certificate, through the support function and the results of real-valued Superpramart, we give the one of Riesz decomposition forms of set-valued Superpramart. It provides new ideas for the research of Riesz decomposition.

Cite this paper

Shuyuan Li,Gaoming Li,Hang Dong,Caoshan Wang, (2016) The Riesz Decomposition of Set-Valued Superpramart. Journal of Applied Mathematics and Physics,04,1275-1279. doi: 10.4236/jamp.2016.47134

References