Vol.3, No.8, 694-701 (2011) Natural Science
http://dx.doi.org/10.4236/ns.2011.38093
Memory and relaxation time of biological systems. An
analysis of the effect of abortion legalization in Italy
Michele Caputo1, Fulvia Gloria-Bottini2
1Department of Physics, University of Rome La Sapienza, Rome; Italy and Department of Geology and Geophysics, Texas A&M
University, Texas, USA;
2Department of Biopathology and Imaging Diagnostics, University of Rome Tor Vergata, Rome, Italy;
*Corresponding Author:
Received 9 August 2010; revised 10 September 2010; accepted 25 September 2010.
ABSTRACT
When a population is affected by a new law
there is a lag between the date of application of
the law and the response of the population;
moreover there is a relaxation time after which a
steady state is reached. The time to maximum
response and the relaxation time may be ap-
proximately estimated from the raw data but the
mathematical modeling of the data allows a
better estimate. The model, when tested on real
data, may be used for future laws or, when ap-
propriately adapted, for other biological sys-
tems also. In this note the memory based model
is tested on the effects of the 1978 law which
legalized the abortions in Italy finding the
response and the relaxation time. It is shown
that Italian population, after the abortion law,
has required about 5 years to have the maximum
effect and about 10 years to reach stability. The
evolution of women life and the changes of the
structure of society in Italy is also discussed.
Keywords: Memory; Abortion; Mathematical Model;
Live-Born Infant; Population Growth
1. INTRODUCTION
The changes occurred in society and human life in the
XXth century are enormous. Most changes seem a con-
sequence of the political evolution and of the economic
growth, the latter mostly due to technological innovation
and to scientific discoveries. These changes have solved
long standing problems but have generated many new
ones.
Among other problems, in the last three decades of the
XXth century, the fertility of women, especially by Ital-
ian population, had a steady and dramatic decrease. We
might state that, concerning the Italian population, are
present at least three events: the practice of abortion, the
decrease of fertility and the increasing of the age of the
mothers delivering infants. These problems are obvi-
ously connected with the profound alterations in econ-
omy, morality, in the culture and in structural changes of
our society which shows limited interest for the new
lives. Dramatic changes occurred during the life of fe-
males favoured by the introduction of contraception and
by the law that liberalized abortions. These new situa-
tions have caused changes in the structure of families
and in the rate of birth.
The problem of the changes in fertility of the Italian
women leads to discuss the effect of perturbations on a
biological system. However, the problems have different
nature and that will imply different discussions.
The scope of this paper is to illustrate how one arrives
to a memory equation, to model mathematically the
evolution of a biological system and to apply the model
of the variations in the rate of the abortions caused in
Italy by the introduction of the 1978 law which liberal-
ized the abortion. The analytical model might be useful
to estimate the delay time of the effects of other types of
perturbations in the evolution of populations.
1.1. The Evolution of Women Life in Italy
An inspection of Figures 1 and 2 suggests that the ef-
fect of the 1978 abortion law on the number of abortions
in Italy is stabilized.
It is then in order to examine the possible impact of
the law on cultural and structural aspects of the popula-
tion in Italy, after that the law was enforced, with special
reference to age-sex distribution. Obviously other im-
portant changes occurred in Italy, mostly in the socio-
economic field, which contributed to the above men-
tioned cultural and structural changes. We will examine
those which seem most relevant from the structural point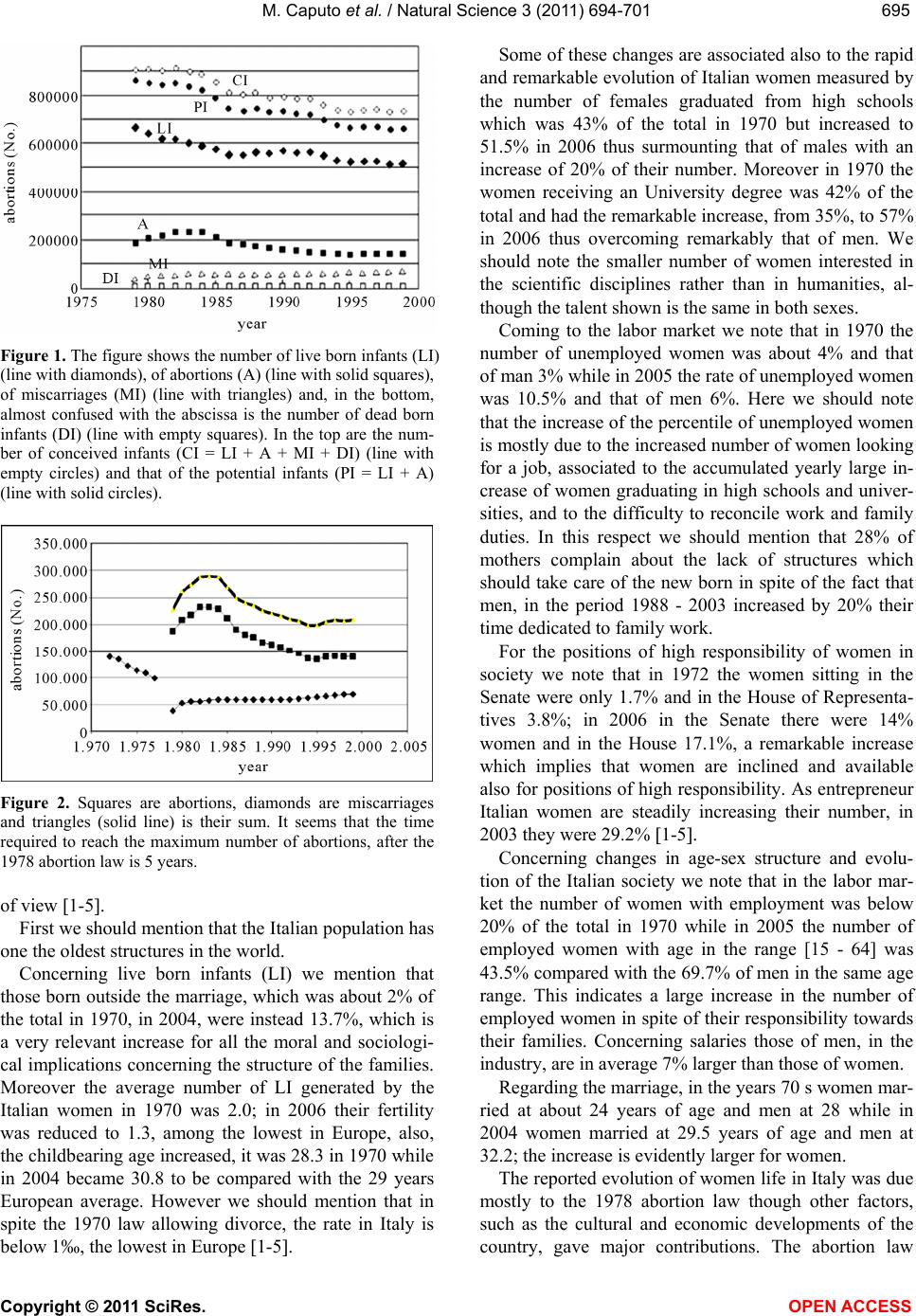

M. Caputo et al. / Natural Science 3 (2011) 694-701
695695
Figure 1. The figure shows the number of live born infants (LI)
(line with diamonds), of abortions (A) (line with solid squares),
of miscarriages (MI) (line with triangles) and, in the bottom,
almost confused with the abscissa is the number of dead born
infants (DI) (line with empty squares). In the top are the num-
ber of conceived infants (CI = LI + A + MI + DI) (line with
empty circles) and that of the potential infants (PI = LI + A)
(line with solid circles).
Figure 2. Squares are abortions, diamonds are miscarriages
and triangles (solid line) is their sum. It seems that the time
required to reach the maximum number of abortions, after the
1978 abortion law is 5 years.
of view 1-5.
First we should mention that the Italian population has
one the oldest structures in the world.
Concerning live born infants (LI) we mention that
those born outside the marriage, which was about 2% of
the total in 1970, in 2004, were instead 13.7%, which is
a very relevant increase for all the moral and sociologi-
cal implications concerning the structure of the families.
Moreover the average number of LI generated by the
Italian women in 1970 was 2.0; in 2006 their fertility
was reduced to 1.3, among the lowest in Europe, also,
the childbearing age increased, it was 28.3 in 1970 while
in 2004 became 30.8 to be compared with the 29 years
European average. However we should mention that in
spite the 1970 law allowing divorce, the rate in Italy is
below 1‰, the lowest in Europe 1-5.
Some of these changes are associated also to the rapid
and remarkable evolution of Italian women measured by
the number of females graduated from high schools
which was 43% of the total in 1970 but increased to
51.5% in 2006 thus surmounting that of males with an
increase of 20% of their number. Moreover in 1970 the
women receiving an University degree was 42% of the
total and had the remarkable increase, from 35%, to 57%
in 2006 thus overcoming remarkably that of men. We
should note the smaller number of women interested in
the scientific disciplines rather than in humanities, al-
though the talent shown is the same in both sexes.
Coming to the labor market we note that in 1970 the
number of unemployed women was about 4% and that
of man 3% while in 2005 the rate of unemployed women
was 10.5% and that of men 6%. Here we should note
that the increase of the percentile of unemployed women
is mostly due to the increased number of women looking
for a job, associated to the accumulated yearly large in-
crease of women graduating in high schools and univer-
sities, and to the difficulty to reconcile work and family
duties. In this respect we should mention that 28% of
mothers complain about the lack of structures which
should take care of the new born in spite of the fact that
men, in the period 1988 - 2003 increased by 20% their
time dedicated to family work.
For the positions of high responsibility of women in
society we note that in 1972 the women sitting in the
Senate were only 1.7% and in the House of Representa-
tives 3.8%; in 2006 in the Senate there were 14%
women and in the House 17.1%, a remarkable increase
which implies that women are inclined and available
also for positions of high responsibility. As entrepreneur
Italian women are steadily increasing their number, in
2003 they were 29.2% 1-5.
Concerning changes in age-sex structure and evolu-
tion of the Italian society we note that in the labor mar-
ket the number of women with employment was below
20% of the total in 1970 while in 2005 the number of
employed women with age in the range [15 - 64] was
43.5% compared with the 69.7% of men in the same age
range. This indicates a large increase in the number of
employed women in spite of their responsibility towards
their families. Concerning salaries those of men, in the
industry, are in average 7% larger than those of women.
Regarding the marriage, in the years 70 s women mar-
ried at about 24 years of age and men at 28 while in
2004 women married at 29.5 years of age and men at
32.2; the increase is evidently larger for women.
The reported evolution of women life in Italy was due
mostly to the 1978 abortion law though other factors,
such as the cultural and economic developments of the
country, gave major contributions. The abortion law

M. Caputo et al. / Natural Science 3 (2011) 694-701 696
allowed women the possibility to avoid bearing an unde-
sired infant, in addition to the already existing possibili-
ties to avoid pregnancies through the existing mechanic-
cal and new chemical contraceptives and to have access
to a life-stile different from the traditional.
1.2. Live Born Infants, Induced Abortions
and Miscarriages (Spontaneous
Abortions) in Italy
We begin with some simple observations on the sta-
tistical information on the evolution of the Italian popu-
lation. The Figure 1 shows the number of LI, the num-
ber of legal abortions (A), the number of miscarriages
(MI), the number of dead born infants (DI), the sum of
LI plus the A plus the MI plus the DI, which is the
number of conceived infants (CI = LI + MI + DI) and,
finally, the sum of LI and A which we define the poten-
tial infants PI (PI = LI + A), that is, those who could
possibly have had birth without the intervention of men.
Note that the percent decrease of PI, from 1979 to
1999 is 0.2318 or 9948.7/year, that of the CI is 0.1905 or
8596.5/year and that of LI is 0.223 or 7495.5/year; that
is the percent decrease of the PI is even more dramatic
than that of LI; fortunately the percent decrease of CI is
smaller than the others.
In modeling the miscarriages, which are independent
of the will of the couple, are not taken into account and
we tentatively assume that all, or almost all, the abor-
tions, which were illegal before the 1978 law and came
on the surface after 1978, were performed in hospitals
and were reported in the official statistics of Istituto Na-
zionale di Statistica 1-5. We realize that this assump-
tion is optimistic and we model the statistics of those
cases and use these data which obviously begin with the
year 1979.
We consider the yearly number of abortions reported
by ISTAT 1-5, without discussing the osmotic phe-
nomena between legal and illegal abortions occurred as a
consequence of the law. We will use an analytic model
with memory and obtain the parameter values resulting
from the fitting of the model to the data; this may be of
help in the discussion of the causes of the yearly varia-
tions in the number of abortions and the interactions
with other phenomena.
The data on abortions show an initial slow increase
due to the time needed to accept the law, the reaction
time, then follows a slow decrease to an almost stable
trend. The scope of our work is precisely the tentative
estimate of the reaction time to the new law and obtain
analytically the time to steady state, the relaxation time,
which may give some indications on the reaction time to
other possible future laws in the same field or in other
fields of demography.
Obviously there was osmosis between illegal (MI) and
legal (A) abortions, this was one of the reason for mak-
ing the 1978 law. Certainly some abortions were made in
Italy outside the rules of the law before 1978 or abroad
but we have no means to evaluate them. However we
have an indirect proof of it in the sudden decrease of the
reported number of MI: from 99.259 in 1977 to 36.558
in 1979 and leveling around 60.000 at the end of the
century as shown in Figure 2, while the number of A in
1979 was almost 200.000 to level around 130 000 at the
end of the century.
This indicates that, probably, before the 1978 abortion
law, many reported miscarriages were in fact abortions.
After the law the latter cases were rightly reported as
abortions which in turn suddenly decreased the number
of reported miscarriages, however after 1978 the number
of reported miscarriages increased by 50% to reach al-
most steady state only in 1985.
2. MEHODS
We illustrate now how one arrives to the memory
equation used for an estimate of the effect of perturba-
tions on the variation rate of A.
The curves modelling the phenomenon, such as the
logistics, are generally obtained from differential equa-
tions expressing in various forms the objective proper-
ties of the number of individuals n(t) of the population
which one desires to model. Among these are the famous
Volterra’s non linear equations and many others. Many
of these equations are written expliciting the growth rate
n’(t), with integro-differential forms of n(t) and n’(t).
Some procedures lead to first or second order differential
equations, often producing converging and/or diverging
solutions; some non linear equations, are discussed ana-
lytically others numerically.
Here we proceed as if the equation represents a bio-
logical system, which in our case is the population pro-
ducing the observed yearly number of A in Italy from
1979 through 1999, and estimate the reaction of the sys-
tem to a perturbation. The data are the number of A in
Italy shown in Figure 1 and the perturbation is the 1978
law which legalized the abortions. The study would have
been more consistent if the data before 1978 were avail-
able but, as we mentioned, they were not reported.
To study the statistic of A we introduce into the equa-
tions governing the population growth a memory mecha-
nism and a perturbation y, in our case the abortion law,
and solve the equation obtaining analytically the effect
of the perturbation to be fit to the data in order to obtain
the memory parameters of the system. The same ap-
proach was used by Caputo and Kolari 6 to solve a
financial problem. Other mathematical methods of analy-
sis of population dynamics may be retrieved from the

M. Caputo et al. / Natural Science 3 (2011) 694-701
697697
vast literature concerning this topic 7-9. Our contribu-
tion to the previous innovative theoretical work on popu-
lation dynamics consists in the introduction of a mathe-
matical memory function in the equation representing
the dynamics of the rate of abortions subsequent to a
perturbation of the system 10.
3. RESULTS
It is seen in Figure 1 that the number of A seems to
have an anomalous increase beginning in the year 1979
and ending in 1994 when it seems to stabilize. This pre-
sumed anomaly gives us an opportunity to study ana-
lytically the yearly number of A and to make tentatively
a model of its evolution in time.
In order to design a model for the effect of the abor-
tion law we must take into account also that their num-
ber, being proportional to the number of CI, must be
linearly adjusted for the decrease of the number of CI.
We then normalized A to the yearly number of CI in the
period 1979 - 1999. The result shown in Figure 3 con-
firms that anomaly in A is real.
To model the anomaly in A we begin considering the
following equation assuming that the population pro-
ducing the abortions behaves as a dynamic system which
can be described by assuming that the output varies over
time as a response to variations of production 11, that
is:


ldr dtkbytcrt  (1)
where r(t) is the yearly number of A produced, y(t) is a
perturbation which may induce changes in the evolution
of the system and therefore in r(t), l is sec, k, b, c are
dimensionless parameters and g is secu. Since c and l are
assumed positive, the standard dynamic analysis implies
that the model is globally stable when y(t) is time inde-
pendent and shows a monotonic adjustment to a new
equilibrium following any change in y.
To introduce the memory we modify Eq.1 introducing
the memory operator gdu/dtu and rewriting it as
 
uu
ldr dtkbytgdydtcrt (2)
The presence of the two parameters b and g related to
y implies the possibility that the memory only partially
affects y in Eq.2 6. The term –gduy/dtu represents the
fading effect of memory.
The mathematical memory mechanism employed is a
mathematical operator called, perhaps improperly, frac-
tional derivative of order u, 12-14, defined as
 
 



0
11d dd
tu
uu
ft tuft

  
(3)
where u is limited in the range [0 - 1], and Γ is the gamma
Figure 3. Number of abortions A adjusted to the variable
number of conceived infants CI.
function. In practice the derivative of fractional order of
f(t) is constructed with a weighted mean of the first order
derivative


dv f





 over the time interval [0-t]. That
is, the values of


dd
v
f





 at time v far apart from t
are given smaller weight than those at times v closer to t.
Hence, the weights are increasingly smaller with in-
creasing time separation from the time t to imply that the
effect of the past is fading with increasing time. When
u = 0 and f(0) = 0, the fractional order derivative reduces
to the functions themselves; when f(t) is a constant its
fractional derivative is zero. Importantly, the weights
multiplying the first order derivative of f(t) inside the
integral appearing in Eq.3 can be chosen in many ways.
The definition adopted in Eq.3 is appropriate because it
is algebraically simple, allows easy solutions, and has
commonly been applied in the previous studies 6.
Being more explicit we note how the memory func-
tion implies its past. For implying the past values as de-
fined by Eq.3, the function is reconstructed by summing
the successive weighted rate of variation in the previous
times. The rates are given by the first order derivative
and the weights by the factor appearing before the de-
rivative (Eq.3). It is important to note that the weights
are decreasing with time starting from time t where the
function is estimated; therefore the effect of the past
rates is fading with the separation from the time t 15 as
it often occurs in human memory. That is the way for
reconstructing the function value from its past values.
Numerous applications of memory functions have
been made in various fields; in mathematical physics 16,
in mechanics 17, in geophysics 18, in hydrodynamics
19,20, in electrical industry 21, in chemistry 22,
biology 23, in medicine 24 and widely in physics
25.
The use of memory functions is increasing in the
physical sciences, and begins to spread also in the re-
search work in many fields. A recent work of Caputo
and Kolari 6 studied the documented fact that increases

M. Caputo et al. / Natural Science 3 (2011) 694-701 698
in inflation rate have a negative short-run but positive
long-run effects on stock returns. In their paper they de-
rive an analytical model of the tax version of the Fisher
equation, that incorporates a memory function for stock
prices and inflation rates and based on fractional calcu-
lus and showed that the knowledge of the relaxation time
of the economy is crucial when trying to drive the
economy with monetary instruments. Importantly, this
model demonstrates that both negative, short-run and
positive, long-run effects are possible in response to an
increase in inflation.
Caputo and Di Giorgio 26 generalized, but also spe-
cialized, this method to model and study the effect of a
prime rate change on the economic system the Keynes-
ian IS-LM model. These results imply that memory
functions are likely useful mathematical operators in the
areas of financial economics wherein parameters have
time dependent behavior.
In biology Cesarone et al. 27 used the memory equa-
tion of diffusion to successfully study the flux through
biological membranes.
Referring to Eq.2, the perturbation to the equation at
the time t consists of by(t), plus the part gduy/dtu, the
latter enters the equation through to the memory effect
(23,27). The factor l appears in Eq.2 for sake of general-
ity since it would allow to discuss the case when l is
vanishing, it is no limitation to assume here that l = 1.
Having little knowledge of the analytic form of the
perturbation y, we may assume that due to the spread of
the information in the system it is initially increasing
with time and that eventually it may reach stability. Of
the many ways to think of it, the simplest form to as-
sume is that it occurs at the time t0, it increases linearly
at a rate a until a time t1 and then will last for an indefi-
nite time; it is represented analytically as follows
y0 when t < t0
y = y0 + a(t – t0) when t0 < t < t1 (4)
y0 + at1 when t1 < t
Really the time variation of the perturbation is not so
simple, other forms may be assumed and investigated
especially their behaviour at the times t0 and t1 where it
probably has a continuous derivative, however the ef-
fects would be on the high frequency part of the spec-
trum of the response while we are interested mostly on
its low frequency portion which is responsible for the
long term changes or relaxation time.
When memory is not present (g = 0, b  0), as shown
in the appendix by Eq.(A5), the perturbation on r caused
by y, assuming y0 = 0 which is no limitation, is
 





 


   


  


000
011
000
111
1exp
1exp
1exp
1exp
bac tct tl Ht t
tctt lHtt
ttlcctt lHtt
ttlcctt lHtt




 







 


(5)
The asymptotic value of (5) is ab(t1 – t0)/c as shown in
the Appendix B.
Since we are seeking the effect of the memory we
may assume in Eq.3 that b = 0 and g  0.
The memory effect on r due to the perturbation y de-
fined in Eq.4 is given by Eq.A6 of the appendix where
we assume l = 1, assume as origin of time that of the
initial time of the perturbation, the abortion law of 1978,
then, t0 = 0. In this case Eq.(A6) reduces.
Formula 6 has been fit to the number of abortions A.
However the number of A, shown in Figure 1, is pro-
portional to the number of CI, the ratio, in the time in-
terval 1979 - 1999, is in the range [0.26 - 0.20] and,
since the number of CI decreases, in order to see the
effect of the perturbation only, the number of A must be
linearly adjusted for the average decrease of the number
of CI. To begin , since the first value of A is in 1979 we
take this year as origin of time; the adjustment is achiev-
ed by dividing the value of A by the corresponding one
of CI and then multiplying the initial value of CI.
The theoretical curve shown in Figure 3 is bell
shaped with nil initial and asymptotic value; for the fit to
the data its maximum is fit to the maximum of the data
which gives the value of ag in Eq.6.
For the fit of the theoretical curve to the data the time
t1 = 5 is retrieved from the data on A (Figure 3), which
indicates that the maximum is reached in 1984. The fit
(Figure 4) is obtained with the values u = 0.6, ag =
219685. The values of u and c define the memory
mechanism, ag, with Eq.6, defines the amplitude of the
perturbation.
It is also clear that the relative number of A seems
stabilized at the end of the century.
4. CONCLUSIONS
The study of the yearly number of the abortions in It-
aly in the period 1979 - 1999 (Figure 2) suggests some
conclusions.
The formulation and the solution of the problem used
    
1
11
11
00
2exp dexp d
tt
tuu
agut vcvv Httt tvcvv



 




(6)

M. Caputo et al. / Natural Science 3 (2011) 694-701
699699
Figure 4. The curves represent the number of abortion per
year.The curve with squares represents the number of abortions
per year adjusted for the decrease of the number of coinceived
infants. The curve with diamond is the theoretical curve ob-
tained from formula (A7) with, u = 0.6 and c = 10 and t1 = 5.
The x-axis unit is the time in years. 1979 is the origin of the
x-axis. The y-axis unit is the number of abortions. Note that the
square and the diamond at t = 5 are superimposed.
in this note may be applied to forecast and to model the
development of future demographic crises.
Our attention is mainly directed to the initial hump in
the yearly number of A (Figure 1) which is related to
the 1978 law that legalized the abortion.
The phenomenology is considered as a dynamic sys-
tem governed by the memory (Eq.2). Estimating that the
time required to reach the maximum number of abor-
tions, after the abortion law of 1978, is about 5 years, we
determined with a mathematical model that the time
needed to reach a steady state is about 10 years, after
which the perturbation is reduced by 60%. This charac-
teristic time, called relaxation time, is of great impor-
tance in the tentative to forecast the effects of future
perturbation that may be caused indirectly or purposely
by cultural changes.
Figure 2 shows that the number of miscarriages is
decreasing since 1972, however the effect of the abor-
tion law of 1978 on the reported number of supposed
miscarriages is evident: they were 99.259 in 1977, re-
duced to 38.558 in 1979 then they reached an apparent
steady state to the value around 60.000. The variation
trend in 1978 would suggest an osmotic phenomenon
between miscarriages and abortions which however
would not affect the reported number of real abortions,
some of which, probably, were previously registered as
miscarriages.
Biological systems tend to a stable equilibrium that is
dependent on genetic heritage and concerning the human
society on cultural heritage also. Any phenomenon in-
ternal or external to human society may upset this stabil-
ity. However like an elastic device, the system tends to
cancel the disturbing effects and to return to a stable
equilibrium.
The mathematical model of biological memory gives
a formal description of elasticity of biological systems.
Tested on real data it can be useful to forecast the con-
sequence of future laws concerning human society and,
appropriately adapted, for the study of other biological
systems.
REFERENCES
[1] ISTAT. (1997) La fecondità nelle regioni italiane. Analisi
per coorti, Anni 1952-1993, Collana Informazioni Noise
Rating 35, Istat, Roma.
[2] ISTAT. (1998) La fecondità regionale nel 1994, Collana
Informazioni Noise Rating 66, Istat, Roma.
[3] ISTAT. (1999) La fecondità regionale nel 1995, Collana
Informazioni Noise Rating 97, Istat, Roma.
[4] ISTAT. (2000) La fecondità regionale nel 1996, Collana
Informazioni Noise Rating 11, Istat, Roma.
[5] ISTAT. (2007) Le statistiche del genere, Approfondimenti,
Istat, Roma.
[6] Caputo, M. and Kolari, J. (2001) An analytical model of
the Fisher equation with memory function. Alternative
Perspectives on Finance and Accounting, 1, 1-16.
[7] Smith, D.P. and Keyfitz, N. (1977) Mathematical de-
mography: selected papers, Springer, Berlin.
[8] Keyfitz, N. and Flieger, W. (1990) World population
growth and aging: demographic trends in the late twenti-
eth century. The University of Chicago Press, Chicago.
[9] Iannelli, M. (1995) Mathematical theory of age struc-
tured population dynamics, Giardini Editori e Stampatori,
Pisa.
[10] Caputo, M., Nicotra, M. and Gloria-Bottini, F. (2008)
Fertility transition: forecast for demography. Human Bi-
ology, 80, 359-376.
doi:10.3378/1534-6617-80.4.359
[11] Caputo, M. (2003) Population self-growth with memory,
Proceedings Meeting: Fenomeni di auto-organizzazione
nei sistemi biologici, Atti convegni Lincei. Accademia
Nazionale dei Lincei, 106, 113-128.
[12] Kiryakova, V. (1999) Generalized fractional calculus and
applications. Pitman Research Notes in Mathematics,
Longman, Harlow.
[13] Podlubny, I. Fractional differential equations. Academic
Press, New York.
[14] Kilbas, A. and Srivastavam, H.M. and Trujillo, J.J. (2006)
Theory and applications of fractional differential equa-
tions. North Holland Mathem, Studies, 204.
[15] Caputo M. and Plastino, (2004) W. Diffusion in porous
layers with memory. Geophysics Journal of International,
158, 385-396. doi:10.1111/j.1365-246X.2004.02290.x
[16] Mainardi, F. (1996) Fractional relaxation-oscillation and
fractional diffusion-wave phenomena, Chaos. Solitons
and Fractals, 7, 1461-1477.
doi:10.1016/0960-0779(95)00125-5
[17] Baleanu, D. and Agraval, O.P. Fractional, (2006) Hamil-
ton formalism within Caputo’s derivative. Czechoslovak
Journal of Physics, 56, 1-11.
[18] Körnig, H. and Müller, G. (1989) Rheological model and

M. Caputo et al. / Natural Science 3 (2011) 694-701 700
interpretation of postglacial uplift. Geophysical Journal
Royal Astronomical Society, 98, 245-253.
[19] Bonilla F.A. and Cushman, J.H. (2000) Role of boundary
conditions on convergence and nlocality of solutions to
stochastic flow problems in bounded domains. Water
Resources Research, 36, 981-997.
doi:10.1029/1999WR900279
[20] Iaffaldano, P., Caputo, M. and Martino, S. (2006) Ex-
perimental and theoretical memory diffusion of water in
sand. Hydrology and Earth System Science, 10, 93-100.
doi:10.5194/hess-10-93-2006
[21] Jacquelin, J. (1984) Use of fractional derivatives to ex-
press the properties of energy storage phenomena in
electrical networks. Technical Report, Laboratoires Al-
catel de Marcoussis.
[22] Le Mehaute, A. and Crépy, G. (1983) Introduction to
transfer motion in fractal media: the geometry of kinetics.
Solid State Ionic, 9&10, 17-30.
[23] Caputo, M. and Cametti, C. (2008) Diffusion with mem-
ory in two cases of biological interest. Journal of Theo-
retical Biology, 254, 697-703.
doi:10.1016/j.jtbi.2008.06.021
[24] El Shaed, M.A. (2003) Fractional Calculus Model of
Semilunar Heart Valve Vibrations. 2003 International
Mathematica Symposium, Chicago.
[25] Naber, M. (2004) Time fractional Schrödinger equation,
Journal of mathematical Physik, 45, 83339-83352.
[26] Caputo, M. and Di Giorgio, G. (2006) Monetary Policy,
Memory and Output Dynamics, In: Monetary Policy and
Institutions, G. Di Giorgio and F. Neri Eds., Essays in
memory of M. Arcelli. Luiss University Press, Guido,
165-176.
[27] Cesarone, F. Caputo, M. and Cametti, C. (2005) Memory
formalism in the passive diffusion across a biological
membrane. Journal Membrane Science, 250, 79-84.
doi:10.1016/j.memsci.2004.10.018

M. Caputo et al. / Natural Science 3 (2011) 694-701
701701
APPENDIX A. THE SOLUTION OF
EQ.2 GIVING THE EFFECT OF THE
PERTURBATION
To solve Eq.2 we use the Laplace Transform (LT)
method. The LT, with variable p, of Eq.2 gives (13)
 
1
00
uu
lpRlrkpbYgpYgypcR

  (A1)
where Y(p) = LTy(t) and R(p) = LTr(t). It is no limitation
to assume that the perturbation is initially nil, y(0) = y0 =
0, then isolating R as function of Y and p we find





0
u
RkplpcbgpYlpc lrlpc 
(A2)
with





  
001
2
01
exp exp
1exp exp
Yatpptpt
ppt pt






(A3)
When memory is absent (g = 0), one finds



 
0R kplpcbYlpclrlpc

  (A4)
When l > 0, c > 0 or l < 0, c < 0, the effect of the perturb-
bation is then









1
000
1exp
LTbY lp c
ba ctcptlHtt



 

(A5)





 
  


 



0010
00
111
1exp
1exp
1exp
tcptlHtttt
lccptlH tt
ttlcctt lHtt

 



 






Since we are seeking the effect of memory we con-
sider the case when all the perturbation is affected by it,
that is b = 0, g  0; this effect is then obtained from (A2)
substituting (A3) with b = 0, we find

 







   
01
01
1
0001 1
00
0011
00
1expd expd
12exp dexp d
u
tt tt
uu
tt tt
uu
LTagpYlpc
agltut tvcvlvHt tt tvcvlvHt t
ut tvcvlvHt tt tvcvlvHt t



















  

 
 


(A6)
Assuming that the perturbation begins at the time t0 = 0 we obtain
 

  
1
1
1
11
00
2expd expd
tt
tuu
u
LTagpYlp caglut vcvlvttvcvlvHt t




 




 (A7)
It is verified, with the help of Eq.A3 and of the ex-
treme value theorem, that the asymptotic value of (A7) is
nil, that is the effect of the perturbation y defined by
Eq.4 is asymptotically nil.
APPENDIX B. THE ASYMPTOTIC
VALUE OF THE EFFECT OF THE
PERTURBATION
The asymptotic value of the effect of the perturbation
is found by first obtaining the explicit expression of R(p),
that is substituting Eq.A3 in Eq.A2,



  

  

001
2
01
exp exp
1exp exp
0
u
Rkplpc abgp
tp ptpt
ppt pt
lp clrlp c

 




 
(B1)
and then applying the extreme value theorem of the LT.
We obtain



 
10
0
lim
p
rpRpkcabttc

  (B2)
Since k/c is the asymptotic value in absence of pertur-
bation, then the asymptotic effect of the perturbation is


10
ab ttc (B3)