Received 13 November 2015; accepted 29 November 2015; published 3 December 2015

ABSTRACT

Density-dependent relations among saturation properties of symmetric nuclear matter and hyperonic matter, the coupling ratios (strengths) of hyperon matter, and properties of hadronic stars are discussed by applying the conserving chiral nonlinear (s, p, w) hadronic mean-field theory. The chiral nonlinear (s, p, w) mean-field theory is an extension of the conserving nonlinear (nonchiral) s-w hadronic mean-field theory which is thermodynamically consistent, relativistic and is a Lorentz-covariant mean-field theory of hadrons. The extended chiral (s, p, w) mean-field model is one of effective models of Quantum Hadrodynamics (QHD). All the masses of hadrons are produced by the spontaneous chiral symmetry breaking, which is different from other conventional chiral partner models. By comparing both nonchiral and chiral mean-field approximations, the effects of the chiral symmetry breaking mechanism on the mass of s-meson, coefficients of nonlinear interactions, coupling ratios of hyperons to nucleons and Fermi-liquid properties are investigated in nuclear matter, hyperonic matter, and neutron stars.

Keywords:

Chiral (s, p, w) Model, Fermi-Liquid Properties of Nuclear Matter, Hyperonic Matter, Neutron Stars

Subject Areas: Nuclear Physics, Nuclear Astrophysics, Many-Body Theory

1. Introduction

A renormalizable quantum field theory based on hadronic degrees of freedom provides us with an intuitively and physically accessible approach from finite nuclei to infinite nuclear matter. The microscopic many-body field theory has been applied to high density neutron and hyperonic matter such as neutron stars in our universe [1] - [12] . The linear neutral scalar and vector (s, w), nonlinear (s, w), and nonlinear (s, w, r) mean-field models are actively studied and applied to finite and infinite hadronic many-body systems. Though hadronic pictures of mean-field models render nuclear and astronomical phenomena readily understandable, they are mainly composed of strongly interacting particles. Those strong interactions make the hadronic approaches and extensions much more complicated. One may investigate the hadronic system by starting from quantum chromodynamics (QCD), because of strong interactions, QCD becomes complicated to apply directly to the nuclear energy domain.

It may be desirable, in principle, to start from QCD, but there are many difficulties in practice, because the QCD coupling is strong at distance scales relevant for the vast majority of nuclear phenomena. Even if it becomes possible to use QCD to describe many-body system of nucleons, this description may not be useful, since quarks cluster into hadrons at low energies, and hadrons are the degrees of freedom actually observed in experiments. A description based on hadronic degrees of freedom is attractive. These are the most efficient at normal densities and low temperatures and for describing particle absorption and emission. Consequently, one is led to introduce certain effective hadronic models to simulate strong interactions of hadrons. Although hadronic models must ultimately fail when the quark and gluon degrees of freedom become essential, we must understand the limitations of hadronic models to isolate and identify true signatures of subhadronic dynamics [11] . The hadronic degrees of freedom have many properties to investigate in terms of nuclear theories and applications (see, discussions in Chapters 2 and 3 in [12] ).

The hadronic mean-field models must be constructed to reproduce the binding energy at the saturation of symmetric nuclear matter (assumed to be −15.75 MeV at 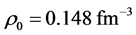or in the current calculation), which is one of the fundamental requirements for nuclear physics. The pressure must vanish at saturation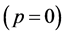, and simultaneously, the self-consistent single particle energy, , must be obtained by the functional derivative of energy density with respect to baryon density, 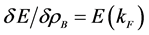, as a dynamical constraint for any employed approximation. The energy density and pressure must maintain a thermodynamic relation, such as 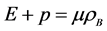(at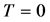), to be a self-consistent approximation for nuclear matter. In terms of dynamical quantities, the self-consistent requirement can be stated that Green function, self-energy and energy density must maintain conditions of conserving approximations, termed thermodynamic consistency. Thermodynamic consistency is explicitly expressed as the requirement that functional derivatives of energy density with respect to self-energies must vanish, [13] , which becomes equivalent to Landau’s hypothesis of quasiparticles and the fundamental requirement of density functional theory [13] - [17] . Any models of hadrons, effective QCD, Lattice QCD which describe nuclear physics must satisfy these conditions of nuclear matter.

The properties of symmetric nuclear matter, such as binding energy at saturation, effective masses and coupling constants, incompressibility and symmetry energy, simultaneously determine binding energy and saturation properties of hyperonic matter; the self-consistent relations are important to examine density- dependent correlations among nuclear and hyperonic matter [7] [8] . The conserving nonlinear mean-field approximation and effective quark models require different coupling constants for hyperons. Since the hyperon coupling ratios, 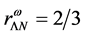, required by SU(6) quark model produce weak density-dependent interactions for hadrons at saturation and high densities, it is not compatible with the coupling ratio, 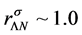, demanded by hadronic nonlinear mean-field approximations. The ratio is necessary to be consistent with properties of nuclear matter at saturation and neutron stars [7] [8] . This property is shown again in the current chiral model at the end of Section 2. The discrepancy of coupling ratios may not be a simple matter, because coupling rations are essentially related to nuclear matter saturation properties. Chiral hadronic models of Quantum Hadro- dynamics (QHD), effective quark models, Lattice QCD models for hadrons must be checked if they maintain conditions of thermodynamic consistency. Then, discrepancies among hadronic and quark models would become constructive to understand respective approaches to nuclear physics.

Although the linear and nonlinear (s, w, r) mean-field models of QHD appropriately simulate properties of symmetric nuclear matter and neutron stars, they have many free parameters, masses and nonlinear coupling constants, coming from meson fields and nonlinear interactions. The upper bounds of values of nonlinear coefficients are confined by maintaining conditions of thermodynamic consistency to an employed appro- ximation and by reproducing empirical data [5] [6] . The results indicate that nonlinear coefficients have tendency to be bounded by conditions of self-consistency when nonlinear interactions are properly renormalized as effective masses and effective coupling constants of hadrons. This could be a manifestation of naturalness for self-consistent approximations [18] - [21] . It is interesting to examine restrictions of nonlinear interactions in terms of self-consistency. The chiral mean-field model may help reveal essential features and strengths of nonlinear interactions [22] - [24] .

Nonlinear (s, p) chiral mean-field approximations were discussed and applied to nuclear matter [25] - [29] . Though density-dependent effects are only generated by nonlinear s interactions, the nonlinear mean-field approximations improved the value of incompressibility in a consistent way, which indicated that nonlinear interactions may compensate for complicated many-body interactions. However, because the physical meaning and relation between nonlinear interactions and a mean-field approximation were not well understood, it was difficult to extend and examine nonlinear mean-field approximations. It is proved that a mean-field appro- ximation with nonlinear interactions is equivalent to Hartree approximation when nonlinear interactions are properly renormalized [5] [6] . Based on the results [5] - [8] and chiral linear and nonlinear models [1] [22] , the current nonlinear (s,p,w) chiral mean-field approximation is developed as a thermodynamically consistent conserving approximation.

The current chiral (s, p, w) mean-field approximation provides the following:

1. Generations of hadron masses by the spontaneous chiral symmetry breaking correspondingly produce coefficients of nonlinear meson interactions. This indicates that the fundamental requirement of nuclear matter saturation is directly related to experimental values of hadron masses 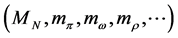and coupling constants. In the mean-field (Hartree) approximation, pion contributions vanish, and s-meson compensates for attractive contributions expected to be given by pions at saturation density. Hence, the saturation property determines the effective mass of the sigma meson,.

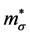2. The coupling constants for hyperons are important for studying phase transitions from -equilibrium asymmetric nuclear matter to hyperon matter, binding energy of pure-hyperon matter and masses of hadronic stars. It is found that the -hyperon coupling ratio to nucleon, , is expected to be by the requirement of nuclear matter saturation and thermodynamic consistency [7] [8] [13] , whereas the SU(6) quark model for hadrons demands, or 1/3 [30] [31] . The differences of result in significant discrepancies in the effective masses of hadrons, onset densities of nucleon-hyperon phase transitions, saturation properties of hyperons, and masses of hadron stars [7] [8] . If the current chiral (s, p, w) mean-field model is applied to phase transition to -equilibrium lambda matter, the coupling ratio: can be deduced (see, Section 3), which is consistent with the analysis of the conserving, nonchiral (s, w, r) mean-field approximation. Although it may be a complicated task more than one expects to reconcile certain consequences derived from effective hadronic and quark theories, one of our purposes is to exhibit discrepancies between effective hadronic and quark theories if there were some indications at nuclear saturation and medium-energy densities. They could be a profound problem for clear comprehension of hadronic and quark approaches to nuclear physics.

The current extended chiral (s, p, w) mean-field model starts from a Lagrangian without hadron masses and generates all the hadron masses and effective coupling constants by way of spontaneous chiral symmetry breaking. This is different from other chiral mean-field models, which introduce the isoscalar-vector w particle externally, in order to produce the repulsive interaction and saturation mechanism. The current chiral (s, p, w) mean-field model produces masses of s, p and w particles by the chiral symmetry breaking mechanism. The chiral symmetric Lagrangian, spontaneous chiral symmetry breaking, and binding energy are discussed in Section 2. Fermi-liquid properties of nuclear matter, such as incompressibility and symmetry energy, K and, and numerical results are shown in Section 3.

Vacuum fluctuation corrections to the chiral (s, p, w) mean-field approximation, applications to b-equili- brium asymmetric nuclear matter and properties of hadron (neutron) stars are discussed in Section 4. The phase transition from symmetric nuclear matter to b-equilibrium hyperon matter, , and important results regarding coupling ratios given by the spontaneous chiral symmetry breaking are also discussed. Concluding remarks are in Section 5.

2. An Extended Chiral (s,p,w) Nonlinear Mean-Field Approximation

The conventional chiral mean-field models for hadrons assume that the Lagrangian with interaction potential, , should be invariant under the chiral transformation and constrain only and mesons as a chiral partner. Moreover, a massive isoscalar vector field is input externally to supply repulsive nuclear- nuclear interactions, as in QHD-I [1] [2] . The conventional chiral mean-field models for hadrons reveal that, when the chiral symmetry breaking parameter vanishes, the masses and also vanish:, , whereas.

We introduce an extended chiral symmetric mean-field Lagrangian for hadrons with the interaction potential. The Lagrangian is invariant under the chiral transformation and produces all hadron masses and nonlinear mean-field interactions by way of the spontaneous chiral symmetry breaking. The parameter a is constant, which will be identified as in the nuclear domain, after chiral symmetry breaking. Therefore, the current extended chiral mean-field model generates w-meson as chiral particles such that all the meson masses are required to vanish simultaneously:, , and when the chiral breaking parameter vanishes,. In other words, we assume that all the hadron masses and nonlinear interactions should be generated by the Lagrangian with interaction potential under the chiral symmetry breaking mechanism.

The current extended chiral mean-filed model that produces all the hadron masses and nonlinear interactions with the chiral symmetry breaking is based on a relativistic chiral model discussed by Walecka, Serot and others [18] [20] [22] - [24] . The extended chiral Lagrangian is

(2.1)

where is the chiral symmetry breaking term. The nucleon is, and are neutral

scalar meson, pseudo-scalar isovector pion and neutral isoscalar omega meson fields, respectively. The field strength tensor is for the vector-isoscalar w-meson. Note that there are no baryon and meson masses in the Lagrangian (2.1). Baryons and mesons are coupled as, and. The coupling constant, g, is the pion-nucleon (and s-nucleon) coupling constant to be required from invariance under the chiral transformation (is assumed).

The Lagrangian (2.1) satisfies SU(2)´ SU(2) ´U(1) global chiral and isospin gauge symmetries, and hence, maintains isospin current and axial current conservations. We introduce the chiral-invariant potential of the following form:

(2.2)

where and are constants determined in the ground state after the spontaneous chiral symmetry breaking. Hence, the free parameters of the current chiral mean-field model are g, and. Note that mesons make the Lagrangian chiral invariant all together, and in this sense, we call mesons chiral particles.

The current chiral Lagrangian is invariant under the following gauge transformations [22] :

(2.3)

where is assumed to be an infinitesimal value, and the meson is invariant under the gauge transformation:. After chiral symmetry breaking, the interaction potential is given in the new ground state as,

(2.4)

where, v, a and are constants determined in the ground state.

The mesons are excited from the new ground state as follows:

(2.5)

where, and are values for the meson fields in the vacuum defined by minimization of (2.4) with respect to, and. The interaction potential V has the following form at the ground state in the new vacuum

(2.6)

and the minimization conditions give

(2.7)

The conditions, and, lead to, , and

(2.8)

The ground state value, , is then defined as:

(2.9)

By expanding the interaction potential V, the terms in (2.6) are collected as follows:

(1) Constant terms are

(2.10)

(2) The terms that are linear in are

(2.11)

This expression vanishes because of the minimization conditions, (2.7) and (2.8).

(3) The terms that are quadratic in are

(2.12)

(4) The terms that are quadratic in are derived in the same way as

(2.13)

(5) The terms that are quadratic in are

(2.14)

and is given by

(2.15)

(6) The remaining cubic and quartic interactions of the meson fields are then given by

(2.16)

The collection of terms from (1) to (6) then yields the interaction potential V written as:

(2.17)

The Lagrangian density (2.1) with the generation of hadron masses by spontaneous symmetry breaking finally takes the following form:

(2.18)

The parameters are identified to be:, and in the nuclear ground state after the spontaneous chiral symmetry breaking.

The SU(2) (global) isospin-symmetry invariance of (2.18) generates the conserved current:

(2.19)

that can be proved to be

(2.20)

from the Lagrangian (2.18) and equations of motion for baryons and mesons. The SU(2) (global) chiral symmetry breaking of (2.18) results in the partially conserved axial-vector current (PCAC):

(2.21)

which is shown to satisfy the PCAC

(2.22)

with the use of equations of motion. The symmetry breaking parameter, , is expressed in the interaction potential (2.6).

The chiral mean-field approximation is defined by replacing meson quantum fields with classical fields:,. They are constants independent of. The spatial part of the vector field should vanish by the requirement of rotational invariance of static and homogeneous nuclear matter [1] . In addition, p-meson contributions vanish in the (mean-field) Hartree approximation. Thus, the chiral mean-field Lagrangian is given by

(2.23)

The equations of motion for the scalar and vector mesons are given by

(2.24)

(2.25)

where is the baryon density:, where is a baryon Fermi-momentum, and is the scalar source given by

(2.26)

The energy density and pressure can be derived from the energy momentum tensor [2] [5] [6] :

(2.27)

(2.28)

where. The scalar source is derived from the functional derivative of with respect to [5] [6] .

The self-consistent effective masses of hadrons are determined by satisfying conditions of thermodynamic consistency [5] [6] :

(2.29)

and self-consistent scalar and vector self-energies are given by [5] [6] :

(2.30)

The self-consistent self-energies (2.30) and single particle energy are essential to understand the effect of coupling constant on the equation of state. Though the single particle energy is a complicated function of coupling constants, it becomes formally simple when nonlinear interactions are renormalized by the condition of thermodynamic consistency in the current chiral mean-field approximation. From the Equation (2.30), the single particle energy behaves, , at high densities. Therefore, the coupling ratio required by SU(6) effective quark model [30] [31] produces smaller single particle energy, , in a hyperonic high density matter. In other words, the single particle energy or chemical potential becomes small when the coupling ratios are employed, resulting in a softer equation of state which becomes difficult to generate observed masses of neutron stars [7] [8] .

The 3-dimensional image of the interaction potential after spontaneous symmetry breaking defined by, is shown in Figure 1. In the current chiral mean-field approximation, the

interaction potential is self-consistently constructed by and mesons. Sigma mesons produce attractive interactions at low densities, whereas omega mesons mainly generate repulsive contributions at high densities. In the chiral (s, p) Hartree approximation, the pion field will vanish completely, and the meson interaction potential in the new ground state becomes only the function of, which has the Mexican-hat type symmetry. In the current paper, the pion field vanishes but the omega field obtains mass. Hence, the current interaction potential after SSB is expressed by. It seems different from the well-known Mexican-hat type potential; however, the potential is bound and produces the Mexican-hat symmetry when the limits, , are taken.

The energy density and pressure satisfy and at all densities. The binding energies of symmetric nuclear matter are shown in Figure 2. The linear (s, w, r) Hartree approximation denoted as MFT-II [1] is listed for comparison in order to see the effect of chiral nonlinear corrections.

3. Fermi-Liquid Properties at Nuclear Matter Saturation

The chiral (s, p, w) mean-field model exhibits remarkable properties when it is compared to the nonchiral, nonlinear (s, w, r) mean-field model. The nonchiral mean-field model is applied to (n, p) symmetric, asymmetric, hyperonic matter, and neutron stars [7] [8] . Although the nonchiral model reasonably simulates properties of nuclear and neutron matter, it has many free nonlinear parameters which cannot be determined uniquely. The upper and lower bound values of coupling constants are constrained by empirical data and self-consistent conditions of approximations. The nonlinear nonchiral mean-field approximations can not clearly explain why values of nonlinear coupling constants are bound in a characteristic way [7] [8] . The chiral symmetry approach sharply restricts nonlinear parameters by the chiral invariance and symmetry breaking mechanism, and it clarifies relations among nonlinear coupling constants, hadron masses and observables.

All the hadron masses and nonlinear coefficients are related to the properties of symmetric nuclear matter, such as binding energy of saturation because the chiral breaking mechanism determines nonlinear interactions in terms of hadron masses and coupling constants, g and, respectively. Consequently, the mass of s-meson, , is related to the binding energy of symmetric nuclear matter (, at) and must be adjusted self-consistently. Incompressibility is calculated by

(3.1)

where is the chemical potential and is equal to the Fermi energy, , because the current chiral mean-field approximation is thermodynamically consistent and Landau’s hypothesis for quasiparticles is maintained. The symmetry energy is calculated by

(3.2)

where is the difference between the proton and neutron density: at a fixed baryon density,.

The coupling constants and effective masses of hadrons and the Fermi-liquid properties of symmetric nuclear matter are listed in Table 1. The effective masses of mesons are shown in Figure 3:, , , at saturation density. The effective mass of a nucleon, , would

be considered to produce a hard EOS and large masses of neutron stars in nonchiral mean-field approximations, but the chiral mean-field approximation produces a softer EOS.

The incompressibility and symmetry energy are shown in Figure 4 and Figure 5, respectively. They are and, at saturation density. These observables are expected to be and in the nonchiral, nonlinear (s, w, r) mean-field approximation [7] [8] . Although the self-consistent chiral (s, p, w) mean-field approximation produces, it improves the value of linear (s, w) mean-field approximation,. As we proved that a mean-field approximation with nonlinear interactions is equivalent to Hartree approximation when nonlinear interactions are properly renormalized [5] [6] , a nonlinear chiral (s, p, w) mean-field approximation will be constructed to be a chiral Hartree (s, p, w) approximation. Hence, a chiral (s, p, w) mean-field approximation should be extended to HF, BHF, ... approximations in order to improve the results. One can notice that r-meson contribution would be important when in the nonchiral (s, w, r) is compared to that of chiral (s, w) in Figure 5. Hence, in order to examine calculations quantitatively, the chiral (s, p, w) model must be extended to the chiral (s, p, w, r) model [32] , which is expected to clarify the chiral hadronic models.

The mass of s-meson is important because all observables, EOS, and masses of neutron stars, depend only on the three adjustable parameters: and coupling constants, g and. The binding energy of symmetric nuclear matter (, at) and the maximum mass of neutron stars suggest that the mass of s-mesons be and. The mass of s-meson seems to be very small compared to the masses employed in other mean-field models. However, the dimensionless parameter, , is similar to the values derived from nonchiral linear and nonlinear mean-field approximations [1] [5] [6] . Binding energies are compared in the Figure 2, and incompressibility, symmetry energy (Figure 4 and Figure 5) and the maximum mass of neutron stars (Figure 9 and Table 1 and Table 2) show reasonable results in the level of relativistic Hartree (s, w) mean-field approximation.

In (Hartree) mean-field approximations, contributions of p-mesons vanish in infinite matter due to spin- saturation, and hence, s-mesons compensate for p-meson contributions in order to produce the saturation mechanism of symmetric nuclear matter. The s-meson produces attractive interactions at low densities with the mass:, which is close to the pion mass. Moreover, is required to obtain solutions that are consistent with those of conserving nonchiral mean-field approximations. If one assumes, solutions are restricted to low densities. However, the chiral mean-field approximation is not appropriate in this case because the interaction potential V shown in Figure 1 becomes unbound and decreases at high densities.

4. Vacuum Fluctuation Corrections and Neutron Star Properties

The full relativistic chiral Hartree approximation, including vacuum fluctuation corrections (VFC), is derived in this section and applied to the properties of neutron stars. The divergent integrals coming from the occupied negative energies (Dirac vacuum) will be rendered finite by including appropriate counterterms in the current chiral Lagrangian. By applying the method discussed in the linear s-w mean-field approximation [1] to the nonlinear s-w-r mean-field approximation [5] [6] , the baryon and meson propagators, self-energies are defined, and appropriate counterterms that make divergent integrals finite are introduced.

The baryon propagator in the mean-field (Hartree) approximation is assumed to be [1] :

(4.1)

where, , is the propagator for negative energy Dirac-sea and is for density- dependent Fermi-sea particles. It can be readily shown that the energy density, pressure and self-energies in Section 2 are computed by assuming. Hence, we recalculate (2.30) by including, which requires renormalization of infinities into physical parameters of the model. By employing the full propagator (4.1) in the chiral nonlinear s-w Hartree approximation, the vector meson self-energy in Equation (2.30) becomes

(4.2)

The first term of vector self-energy (4.2) is a divergent integral evaluated using the technique of dimensional regularization as follows:

(4.3)

where the first term of integration is performed in n dimensions, and the final result of any calculation will be obtained by taking the physical limit. The integral (4.3) vanishes by symmetric integration, which indicates that counterterm corrections (CTC) for the chiral mean-field (Hartree) approximation are produced only by way of f fields.

The counterterms that make the scalar self-energy finite are evaluated by expanding the full propagator of in a power series in the renormalized scalar self-energy. Using the Dyson equation, is formally expanded as:

(4.4)

Insertion of this expression into the scalar self-energy produces

(4.5)

It is clearly shown that the terms of in (4.5) have divergence when the power counting of q is performed in the physical dimension. These divergences can be removed by including the counterterm contribution in the Lagrangian density [33] :

(4.6)

The coefficients of are evaluated explicitly by dimensional regularization [1] . They are given by

(4.7)

The Lagrangian density, , is related to the self-energy by the functional derivative as:

(4.8)

and the full self-energy is finally calculated as:

(4.9)

The full energy density is calculated using the energy-momentum tensor and (4.6), (4.7) as:

(4.10)

The vacuum expectation value of the energy density defined in the limit is given by

(4.11)

The finite vacuum fluctuation correction to energy density is determined from (4.6) as, and is calculated as follows:

(4.12)

Pressure is given by, which is obtained by an energy-momentum tensor as:, (i is summed,). The VFC gives repulsive contributions for all densities. The model parameters, , g and, must be adjusted and fixed to reproduce saturation of nuclear matter, where pressure and must be satisfied.

The effective masses of baryons and mesons, including VFC, are shown in Figure 6. At saturation density, they are, ,. Meson effective masses are almost unity around saturation. The baryon effective mass increases slightly at saturation, which produces a softer EOS at high

densities and decreases the masses of neutron stars. The scalar source is decreased a little by VFC, and accordingly, other fields are similarly decreased by self-consistent relations required by thermodynamic consis- tency. The coupling constants and effective masses of hadrons and the Fermi-liquid properties of symmetric nuclear matter including VFC are listed in Table 2.

The incompressibility and symmetry energy with VFC are shown in Figure 7 and Figure 8, respectively. These Fermi-liquid properties are almost similar at saturation density, but incompressibility, K, is softened at high densities. This character shows that the effect of VFC is noticeable at high densities but is not so important at low densities. The symmetry energy, including VFC, gives similar results as discussed in Section 3. One can see from Figure 8 that the dominant contribution to should be expected from r-mesons, and in addition, Fock-exchange corrections produce important contributions to and K [34] [35] . Hence, it would be generally desired to analyze properties of nuclear matter by employing Hartree-Fock and Brueckner HF approximations.

The phase transition from b-equilibrium to or matter is discussed in the article [7] [8] . The hyperon-onset densities depend explicitly on nucleon-hyperon coupling ratios, and or). They are given by

(4.13)

where, and is a density-dependent coupling constant; is the lowest binding energy of a hyperon. The coupling ratios are required to be and in the nonchiral, nonlinear (s, w,

r) mean-field approximation in order to obtain optimum empirical values of symmetric nuclear matter and neutron stars.

When chiral symmetry breaking is applied to phase transitions from to or matter, it supports the results that coupling ratios should be, which is explained as follows. In (s, p, r) chiral symmetry breaking models, s-mesons generate the mass of nucleons in the new ground state: and. Let us include baryons in the Lagrangian (2.1). The s-hyperon coupling constants are, respectively. Suppose that the ground state expectation value is equipartitioned to baryons in the new ground state after chiral symmetry breaking. Then, one obtains, and it results in

(4.14)

The hyperon coupling ratios in the ground state of nuclear matter are.

These values agree with those concluded independently in the calculation of the nonchiral, nonlinear (s, w, r) conserving mean-field approximation. The hyperon coupling ratios, , are derived from the saturation condition of binding energy of pure-hyperon matter. Let us suppose that binding energy of pure-hyperon, for example, pure-lambda matter is self-bound as is symmetric nuclear matter. Then, one can produce saturation by computing energy density of pure-lambda matter by employing (s, w) mean-field approximation. However, as it is proved in the paper [7] [8] , the coupling ratios are constrained by the Equation (4.13). With the constraints, the coupling ratios that produce saturation of hyperon matter are shown to be. If the coupling ratios are or as suggested by the SU(6) effective quark model [30] [31] , it is not possible to produce saturation of binding energy of pure-hyperon matter, which is a fundamental error as a self-consistent theory of nuclear matter [36] . This is one of conclusions from the hadronic (s, w, r) mean-field approximation [7] [8] ; the current chiral model and results (4.14) agree and support the conclusion of coupling ratios.

The masses of neutron stars are calculated using the Tollman-Oppenfeimer-Volkoff (TOV) equation [37] , energy density and pressure obtained in Section 3 and Section 4. They are shown in Figure 9 as a function of a central energy density,. Vacuum fluctuation correction softens EOS and reduces the maximum mass of neutron stars by about 20%. It should be noticed that the conserving nonlinear, nonchiral (s,w) mean-field approximation [5] [6] produces similar results for K, , , when and are assumed. Hence, the chiral symmetry breaking mechanism provides a consistent method for understanding solutions to nonchiral, nonlinear mean-field models.

5. Concluding Remarks

In the current extended chiral mean-field model, all the masses of baryons and mesons are produced through

spontaneous chiral symmetry breaking of nonlinear interaction potentials. Adjustable free parameters are limited to, g and after the hadron masses are identified and fixed in the nuclear domain, e.g., and. Constraints on the chiral mean-field approximation are properties at saturation (, at) and the maximum mass of isospin-asymmetric neutron stars. The mass of s-mesons is determined to maintain the constraints and is given by , which is also necessary so that the interaction potential V is positive and bounded at high densities. One should note that the dimensionless parameter, which is known to characterize finite and infinite nuclear systems [1] [5] [6] , is similar to those of linear and nonlinear mean-field approximations. Hence, the current chiral mean-field approximation is compatible with results obtained by other QHD (s, w) Hartree approximations and improves some of properties for infinite nuclear matter. The coupling constant and effective mass, and, must be considered together, because and constitute density-dependence and chiral-symmetry of the model. The chiral mean-field approximation indicates that a scalar particle less than the mass of p-mesons should be needed to produce saturation of nuclear matter.

The effective masses of nucleons and mesons, , are similar to those derived from conserving nonchiral, nonlinear (s, w) mean-field approximations. The effective mass of a nucleon monotonically decreases, but the effective masses of mesons are, at or around saturation density. The vacuum fluctuation corrections exhibit repulsive effects for all densities, but after adjusting coupling constants to reproduce properties of saturation and neutron stars, the effect of VFC is noticeable at high densities but less significant at saturation. The effect of nonlinear interactions is more important than that of VFC in the Hartree approximation. A similar conclusion is also obtained in the nonchiral, nonlinear (s, w, r) mean-field approximation. As shown in Figure 5, r-mesons give noticeable contributions, so the chiral nonlinear mean-field approximation should be extended by including r-mesons.

The nonchiral, nonlinear (s, w, r) mean-field approximations have many adjustable nonlinear coupling constants. The nonlinear coupling constants have upper bounds restricted by self-consistent conditions to approximations and properties of saturation and neutron stars [5] [6] , which are expected as a manifestation of naturalness of nonlinear coefficients [18] - [21] . The current chiral mean-field approximation determines all the nonlinear constants in terms of three adjustable parameters:, g and. The masses of mesons, and, are identified and fixed by experimental values, after chiral symmetry breaking. The nonlinear constants expressed by, g and support the properties of naturalness and the bounded values of nonlinear constants given by nonchiral, nonlinear (s, w, r) mean-field approximations. Self-consistent and optimum solutions to the nonchiral, nonlinear (s, w) mean-field approximation with and become similar to those of the chiral (s, w) mean-field approximation, suggesting that chiral symmetry serves to restrict solutions to nonlinear mean-field approximations.

Because chiral symmetry breaking relates nonlinear coefficients to hadron masses, the chiral mean-field approximation suggests that nucleon-proton and nucleon-hyperon coupling ratios are given by ratios of hadron masses, such that and. It is remarkable that the values of the coupling ratios are consistent with those obtained by the conditions at hyperon-onset density, which are determined by the requirement of thermodynamic consistency at the saturation of hyperon matter [7] [8] . The coupling ratios produce reasonable density-dependent properties of nuclear matter and neutron stars in the calculation of conserving nonchiral, nonlinear (s,w,r) mean-field approximations. On the contrary, the coupling ratios given by the SU(6) quark model for vector coupling constants [31] [30] are expected to be and, but the ratios do not generate consistent results for properties of nuclear and neutron matter. These values produce significantly softer EOS when the values are used in the chiral hadronic model.

The vacuum fluctuation correction softens EOS at high densities, which will be softened further when hyperons are generated. This fact is also consistent with the results derived from the nonchiral, nonlinear (s, w, r) mean-field approximation [9] . Because chiral symmetry breaking clarifies relations among nonlinear interactions, it is important to understand how hyperon-onset densities, binding energy and saturation properties of hyperon matter, and masses of hadron and hadron-quark stars will be modified by chiral models of hadrons. The chiral symmetry breaking mechanism helps us understand the physical meanings of chiral symmetry in masses and coupling constants of hadrons.

The pion contributions begin to appear from the level of HF approximation, and the (s, p, w) chiral mean- field model must be extended to (s, p, w, r) [32] and more sophisticated approximations, such as conserving chiral HF and BHF approximations. The extensions and applications to finite and infinite nuclear systems should be investigated quantitatively, which is important to understand hadron-quark nature of strong interac- tions. The problems of high-energy hadron scatterings and properties of infinite matter, such as hadronquark stars, suggest that hadronization from QCD and phase transitions from bound state hadrons to quark matter could be an important topics in the near future. Quantitative analysis in terms of both quantum hadrodynamics (QHD) and QCD is necessary.

Cite this paper

Schun T. Uechi,Hiroshi Uechi, (2015) Density-Dependent Properties of Hadronic Matter in an Extended Chiral (σ, π, ω) Mean-Field Model. Open Access Library Journal,02,1-18. doi: 10.4236/oalib.1102011

References