Open Access Library Journal
Vol.02 No.11(2015), Article ID:68886,10 pages
10.4236/oalib.1102171
Ship Nonlinear Rolling and Roll Angle Reconstruction Based on FIR
Jianhui Lu1,2*, Chunlei Zhang2, Shaonan Chen2, Yunxia Wu2
1Shandong Province Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao, China
2College of Engineering, Ocean University of China, Qingdao, China

Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 November 2015; accepted 18 November 2015; published 23 November 2015

ABSTRACT
The paper analyzes the nonlinear damping torque and nonlinear restoring moment and establishes the nonlinear motion equation of ship rolling under random sea. The Runge-Kutta method is used in the time domain to solve the equation, and to simulate the time history of random wave excitation ship rolling and free decay process. This paper used the ship attitude inertial measurement system and its algorithm technology to construct the ship rolling angle from the acceleration measuring signals and to simulate the angle acceleration measurement signal. To study on test conditions of these parameters and the method to improve the accuracy of parameters, the effect of acceleration measurement noise on angle reconstruction accuracy is studied. Under SNR 20, reconstructed angle RMSE is 0.0019 rad. Studies show that the inertial measurement system and algorithm can effectively reconstruct ship rolling angle from the acceleration measurement signal, and the algorithm has the ability to suppress measurement noise.
Keywords:
Ship Rolling, Inertial Measurement, Sensitivity Study, Reconstruction Technology
Subject Areas: Fluid Mechanics

1. Introduction
The important research topic of shipping industry is stability and seakeeping problem, because of interference wave will lead to roll, pitch, yaw, heave, surge and sway motion. To get the angular displacement parameters is the basis of ship roll reduction control. Nayfeh, A.H. and Khdeir, A.A. [1] [2] have used multi-scale method to study in regular waves with steady and non-steady ship inclination angle under rolling motion, to obtain two order perturbation solutions. Nayfeh, A.H. and Sanchez, N.E. [3] have used multi-scale method to study the ship nonlinear rolling motion in the long wave, and to discuss the parameter resonance and the main parameters of resonant characteristics. Eissa, M. and EI Bassiuny, A.F. [4] have considered the righting moment of the linear, two order terms, three squares, five squares and seven squares and damping torque of the linear and cubic terms and other conditions, using the method of multiple scales to study problem of nonlinear ship rolling in regular beam sea. Feng Tiecheng [5] has studied the parametric excitation of transverse waves rolling to solve the parametric excitation equation of motion in the time domain, and further analyzes the parametric excitation and the relationship between the rolling response and ship security. Based on the concept of static stability, Lin Yan and Ji Zhuoshang [6] have used multi-scale method to calculate the approximate analytical solution of ship rolling motion equation under the condition of transverse wave, and the stability condition of the roll. Yuan Yuan and Yu Yin [7] have studied the resistance of capsizing of ship in regular beam sea from the angle of nonlinear dynamic stability of the system.
Based on engineering demand, the ship displacement (linear displacement and angular displacement) measurement is widely concerned. The ninth reference is studied on ship motion inertial measurement and reconstruction technology for the displacement, providing essential ship maneuvering, dynamic positioning, and active anti rolling displacement motion parameters. In this paper, ship rolling model is established, and the simulation of ship rolling motion on the random sea, the building of ships attitude strapdown inertial measurement system and its algorithm, the simulation of ship rolling angle acceleration measurement signal in the reconstruction of rolling angular displacement, the method also can be used in acceleration of ship heaving and displacement measuring signal reconstruction line.
2. Random Wave Excitations of Ship Rolling Modeling and Simulation
Model of random sea waves can be divided into 2-D irregular wave model and 3-D irregular short crested wave model of random sea waves. This paper uses 2-D irregular wave, simulation of ship in random waves on the roll motion. Firstly the obliquity of wave model is established, and simulation of wave obliquity. In this paper, the comparison between 2-D irregular wave model and the 3-D irregular wave model is not the key point.
2.1. The Slope of Wave Surface Model and Spectrum
The ship is sailing in the waves, the waves of disturbance torque is mainly related to the slope of wave surface. The slope of wave surface can be regarded as zero mean stationary random process; the waves in the slope of wave surface between the fixed points can define by the slope of wave surface spectrum
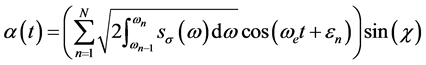 (1)
(1)
where w is the circular frequency;  is in the
is in the  uniformly distributed random phase angle; N is the number of selected harmonic;
uniformly distributed random phase angle; N is the number of selected harmonic; 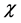 is the course angle, encounter angle frequency speed;
is the course angle, encounter angle frequency speed; 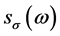 is the wave slope spectrum function, can be obtained by the wave spectrum function
is the wave slope spectrum function, can be obtained by the wave spectrum function 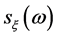
 (2)
(2)
where g is the acceleration of gravity.
2.2. Long Crested Waves Spectrum
By the type of wave obliquity model 2 to build random waves must determine the wave spectrum. The ship wave spectrums have a relationship with the actual environmental conditions. At present, the most application wave spectrum density are Pierson-Moscowitz spectral spectrum (PM) [8] , ITTC double parameter spectrum (ISSC spectrum), JONSWAP spectrum, etc., for ITTC recommended JONSWAP is the development of the ocean. PM spectrum is suitable for the full development of infinite depth of the sea, it is widely used in ocean engineering and marine engineering field, this paper uses the PM spectrum. The revised PM spectrum form is
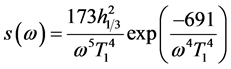 (3)
(3)
where 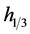 is the significant wave height,
is the significant wave height, 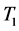 is the mean wave period.
is the mean wave period.
2.3. Long Crested Random Waves Spectrum Simulation
When average water depth is 20 m in Bohai sea area, the long crested random ocean wave angle by simulation in different sea conditions, Figure 1 shows that the significant wave height is 1 m, mean wave period is 7 s, zero speed, heading angle (beam seas) the wave inclination simulation curve.
3. The Mathematical Model of Ship Rolling Motion
Due to the unpredicted rough wave, ship rolling, pitching, yawing angle displacement and swaying, surging, heaving linear displacement motion will occur in the navigation. The rolling is most likely to occur and the amplitude is large, when the ship rolling damping is small, then the performance of ship rolling is an important index to judge the performance of a ship. Affected by the structural characteristics and wave disturbance, the ship rolling model is nonlinear. When the rolling angle is small, usually the ship’s rolling model is linearization. The purpose of this paper is through the measurement of acceleration (measurable) to reconstruct the displacement, ignoring the ship pitching, yawing motion and sway, surge, heave motion on the coupling effect of ship rolling, establishing the nonlinear ship rolling model. In the two-dimensional long crested random waves, the ship rolling motion equation is every moment in the ship rolling direction balanced results; motion equation of the ship is
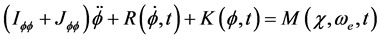 (4)
(4)
where  is the hull of its moment of inertia;
is the hull of its moment of inertia;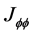 is additional mass moment of inertia;
is additional mass moment of inertia; 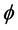 is the ship roll angle;
is the ship roll angle;  is roll damping moment;
is roll damping moment; 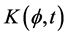 is roll restoring moment;
is roll restoring moment; 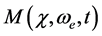
moment, 





Figure 1. Wave inclination simulation curve.
where D is vessel displacement, B is vessel width, 
When the rolling angle is large rolling damping moment is nonlinear, at present there are mainly two forms. Froude puts forward the linear damping plus square damping and Hadarra [10] puts forward linear damping and cubic damping. Linear damping and cubic damping form

Changes of restoring moment are more complex, because there are the ship rolling, pitching, heaving, wave front rise higher and the impact of the change over time, which can be expressed as

where GZ is the recovery of arm function of ship, 



where GM is the initial stability of the vessel, gm(t) is pitching, heaving, wavefront increased stability due to the high initial term changes, 

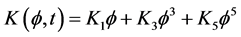
where



where h is transverse stability; 
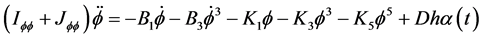
The above formula with both sides divided by

where


4. The Ship Rolling Simulation
Taking a fishing boat used in the literature 10 for example [12] , to study the ship rolling motion, rolling parameters obtained from the test, the vessel basic parameters in Table 1 and Table 2.
Take the harmonic frequency step size


Table 1. The basic parameters of the ship’s structure.
Table 2. The basic parameters of the ship roll motion.
6.3˚, the standard deviation of the roll angle will reach 2.2059˚, when the significant wave height is 4 m, the maximum roll angle of up to 22.4˚, the standard deviation of the roll angle will reach 8.1990˚, because the simulation of wave frequency is consistent with the ship rolling natural frequency.
And then we discuss the factors influence the ship rolling, including external excitation and sensitivity analysis of empirical parameters.
4.1. The Influence of External Excitation on the Ship Rolling
Figure 2 shows that, at the beginning, the value of ship rolling increases gradually with the mean wave period being increased. When the mean wave period is 5 s, the ship rolling variance is maximal, and then it decreases with the increase of the mean wave period. So the results shown in Figure 2 are achieved.
The results of the significant wave height are shown in Figure 3. We notice that the significant wave height will have a significant impact on ship rolling. The ship rolling gradually increases with the increase of the significant wave height. So we choose the typical parameters to calculate.
4.2. Sensitivity Analysis of Empirical Parameters
Figure 4 shows the influence of the total mass moment of inertia on the ship rolling. We notice that the total mass moment of inertia will have a significant impact on the ship rolling. When the total mass moment of inertia is 1250/tm2, the ship rolling variance is maximal, and then it decreases with the increase of the total mass moment of inertia, because the total mass moment of inertia influences the natural frequency of ship rolling.
Figure 5 shows the influence of b1. We notice that b1 will have a significant impact on the ship rolling. When b1 is 0.017, the ship rolling standard deviation is maximal, and then it is essentially unchanged.
The results of b3 are shown in Figure 6. The ship rolling increases quickly with the increase of b3. In the center of 0.0165, the value of 30% range is approximate linear variation, so the estimated value of this parameter should be very careful, then I studied the relationship between the changes b3 and the mean wave period with the ship rolling. From Figure 6, we can see that for any mean wave period, b3 has the similar trend.
Figure 7 shows the influence of k1 on the ship rolling. When k1 is 1.65, the ship rolling standard deviation is maximal, and then it decreases with the increase of k1. k1 represents the water displacement of ships and ship the metacentric height, the wavefront of the elevated lead to metacentric height changes, then influence the ship rolling.
The results of k3 are shown in Figure 8. The ship rolling increases quickly with the increase k3. And when k3 reaches −0.75, the ship rolling standard deviation is maximal. Then, it decreases with the increase of k3.
Figure 9 shows the influence of k5 on the ship rolling. Firstly the ship rolling gradually increases with the increase of k5. When k5 reaches 0.07, the ship rolling standard deviation is maximal, and then it decreases with the increase of k5.
In summary, from the simulation results, the moment of inertia have great influence on ship rolling, in order to get the precise value of the moment of inertia, we must modified calculation moment of inertia based on the actual shipment, In addition to b1, other parameters have significant effects on rolling, therefore, to study on test conditions of these parameters and the method to improve the accuracy of parameters.
5. Rolling Angle Reconstruction Based on FIR
5.1. The Sensor Configuration for Measurement
In order to get the ship attitude angle and acceleration parameters, sensor placement scheme as shown in Figure 10. Measuring system consists of three groups consisting of vertically mounted sensor, each comprising an angular rate and acceleration sensors.
Figure 2. The influence of mean wave period on the ship rolling height.
Figure 3. The influence of the significant wave.
Figure 4. The influence of the total mass moment of inertia on the ship rolling.
Figure 5. The influence of b1 on the ship rolling.
Figure 6. The influence of b3 and mean wave period on the ship rolling.
Figure 7. The influence of k1 on the ship rolling.
Figure 8. The influence of k3 on the ship rolling.
Figure 9. The influence of k5 on the ship rolling.
Figure 10. The sensor configuration for measurement.
The second-order integration filter is the key to design acceleration reconstruction displacement method [13] [14] . The ideal frequency response,

The designing method of second order integral filter is included digital filtering method and frequency domain integral method, the ninth literature studied that the design methods of FIR filter, then filter parameters are obtained.
5.2. Rolling Angle Reconstruction
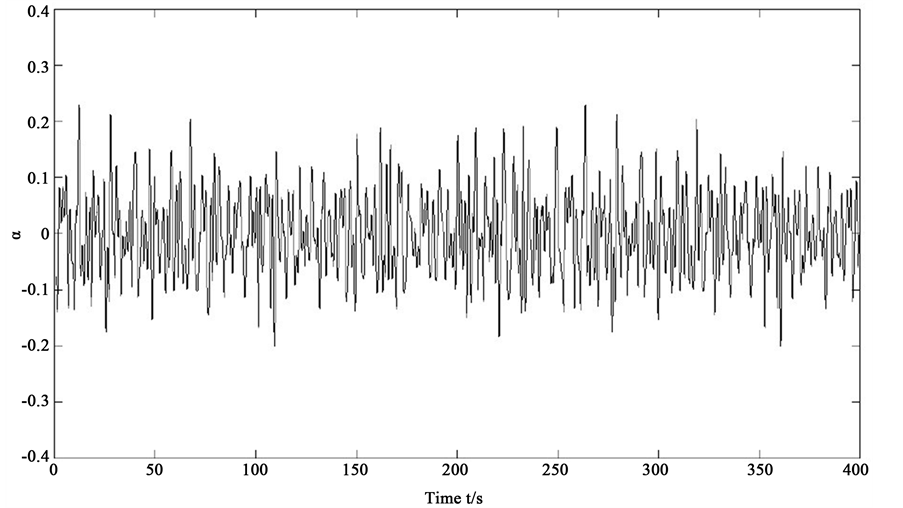
In the random wave excitation for ship rolling motion, when removed wave interference moment, the ship rolling into the free state. Random wave feature wave height is 1m; the mean wave period is the 4.76 s MPM spectrum, course angle is

The rolling angle equation of the second derivative is to get ship’s roll angle acceleration information. Ship rolling angular acceleration frequency is 0.23 hz, FIR filter target frequency is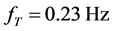

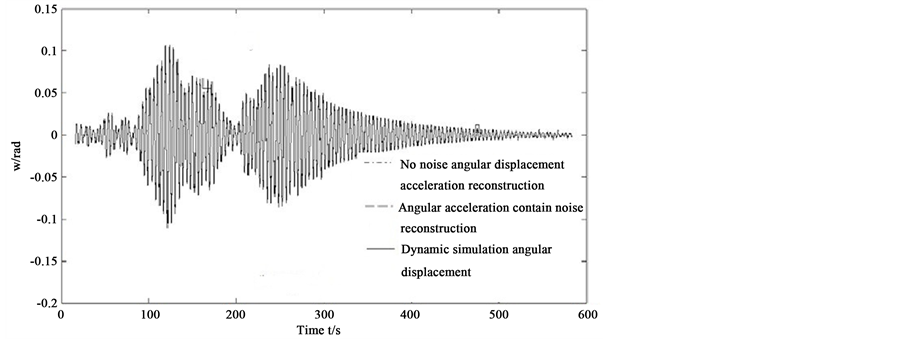
In the wave excitation of 0 - 300 s and free rolling 300 s - 600 s, there were no significant difference between the FIR reconstruction of angular displacement and dynamic simulation of angular displacement in amplitude and phase, as shown in Figure 11. Table 3 lists the angular acceleration of simulation and reconstruction angular displacement under the condition of wave excitation and free roll of root mean square error (RMSE). The signal-to-noise ratio of 20 Gaussian white noise, leading to the random wave excitation rolling acceleration root- mean-square deviation of 0.013 rad・s−2. In the excitation wave rolling, reconstruction of angular displacement of RMSE in with measurement noise for 0.0019 rad, in the absence of measurement noise for 0.0012 rad. Research shows that design of FIR filter can effectively reconstruct displacement from the acceleration signal, and has the strong ability of noise suppression [15] . This article does not give the filter size for filter coefficient curve second zero value, its filtering effect is basically the same.
Figure 11. Simulation of ship rolling angular comparison with FIR reconstruction.
Table 3. Reconstruction of the angular of the root mean square error.
6. Conclusion
The ship displacement measurement is the key link to ship attitude control, dynamic positioning, offshore construction operation, etc. The paper analyzes nonlinear damping torque and nonlinear restoring moment and establishes the nonlinear motion equation of ship rolling under random sea. The Runge-Kutta method is used in the time domain to solve the equation, and to simulate the time history of random wave excitation ship rolling and free decay process. To simulate the angle acceleration measurement signal, the paper uses the ship attitude inertial measurement system and its algorithm technology to construct the ship rolling angle from the acceleration measuring signals. From the simulation results, the moment of inertia has great influence on ship rolling. In order to get the precise value of the moment of inertia, we must modify calculation moment of inertia based on the actual shipment. Studies show that the inertial measurement system and algorithm can effectively reconstruct ship rolling angle from the acceleration measurement signal, and the algorithm has the ability to suppress measurement noise.
Cite this paper
Jianhui Lu,Chunlei Zhang,Shaonan Chen,Yunxia Wu, (2015) Ship Nonlinear Rolling and Roll Angle Reconstruction Based on FIR. Open Access Library Journal,02,1-10. doi: 10.4236/oalib.1102171
References
- 1. Nayfeh, A.H. and Khdeir, A.A. (1986) Nonlinear Rolling of Biased Ships in Regular Beam Waves. International Ship-building Progress, 33, 84-93.
- 2. Chang, Z.Y., Tang, Y.G., Yang, J.M. and Wang, L. (2012) Analysis for the Deployment of Single Point Mooring Buoy System Based on Multibody Dynamic Method. China Ocean Engineering, 26, 295-506.
http://dx.doi.org/10.1007/s13344-012-0037-x - 3. Ju, S., D., Chang, Y., J. and Chen, G.M. (2012) Envelopes for Connected Operation of the Deepwater Drilling Riser. Petroleum Exploration and Development, 39, 105-110.
http://dx.doi.org/10.1016/s1876-3804(12)60022-6 - 4. Nayfeh, A.H. and Khdeir, A.A. (1986) Nonlinear Rolling of Ships in Regular Beam Waves. International Shipbuilding Progress, 33, 40-49.
- 5. Liu, Q. (2011) Preliminary Study on Simulation for Oil Drilling Rig Hoisting System of AC Conversion Electric Driven Drilling Rig. Oil Field Equipment, 40, 10-15.
- 6. Sanchez, N.E. and Nayfeh, A.H. (1990) Nonlinear Rolling Motions of Ships in Longitudinal Waves. International Shipbuilding Progress, 37, 247-272.
- 7. Eissa, M. and EI-Bassiuny, A.F. (2003) Analytical and Numerical Solutions of a Non-Linear Hip Rolling Motion. Applied Mathematics and Computation, 134, 243-270.
http://dx.doi.org/10.1016/S0096-3003(01)00279-X - 8. Feng, T.C. and Tao, Y.S. (1995) Excitation of Roll and Its Effect to Safety of Ship. Journal of Hydrodynamics, 10, 42-47.
- 9. Hu, J., Tang, Y.G. and Li, S.X. (2013) Vibration Test and Assessment for an Ocean Drilling Rig Derrick: Taking the ZJ50/3150DB Drilling Rig as an Example. Petroleum Exploration and Development, 40, 117-120.
http://dx.doi.org/10.1016/S1876-3804(13)60014-2 - 10. Lin, Y. and Ji, Z.S. (1993) A Study of Ship Rolling Motion and Stability in Waves. Shipbuilding of China, 122, 37-46.
- 11. Sulaiman, O.O. and Magee, A. (2013) Mooring Analysis for Very Large Offshore Aquaculture Ocean Plantation Floating Structure. Ocean and Coastal Management, 80, 80-88.
http://dx.doi.org/10.1016/j.ocecoaman.2013.02.010 - 12. Yuan, Y., Yu, Y. and Jin, X.D. (2003) Undesirable Ship Capsizal in Regular Beam Sea. Journal of Shanghai Jiaotong University, 37, 995-990.
- 13. Tang, Y.G., Zheng, J.W. and Dong, Y.Q. (1998) Study on Synamic Behavior of Ship’s Internal Resonance. Shipbuilding of China, 143, 19-26.
- 14. Senjanovic, I., Parunov, J. and Cipric, G. (1997) Safety Analysis of Ship Rolling in Rough Sea. Chaos Solitons & Fractals, 8, 659-680.
- 15. Chen, S.N. (2012) Anti-Roll Gyro Stabilizer Design and Control for Ships. Ocean University of China, Qingdao.
NOTES
*Corresponding author.