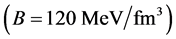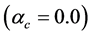Open Access Library Journal
Vol.02 No.11(2015), Article ID:68877,16 pages
10.4236/oalib.1102012
Hardon-Quark Hybrid Stars Constructed by the Nonlinear s-w-r Mean-Field Model and MIT-Bag Model
Schun T. Uechi1, Hiroshi Uechi2
1Department of Physics & Astronomy, The University of Georgia, Athens, GA, USA
2Osaka Gakuin University, Suita, Osaka, Japan

Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 29 October 2015; accepted 13 November 2015; published 18 November 2015

ABSTRACT
Density-dependent relations among saturation properties of symmetric nuclear matter and hyperonic matter, properties of hadron-(strange) quark hybrid stars are discussed by applying the conserving nonlinear s-w-r hadronic mean-field theory. Nonlinear interactions that will be renormalized as effective coupling constants, effective masses and sources of meson equations of motion are constructed self-consistently by maintaining thermodynamic consistency to the mean- field approximation. The coupling constants expected from the hadronic mean-field model and SU (6) quark model for the vector coupling constants are compared; the coupling constants exhibit different density-dependent results for effective masses and binding energies of hyperons, properties of hadron and hadron-quark stars. The nonlinear s-w-r hadronic mean-field approximation with or without vacuum fluctuation corrections and strange quark matter defined by MIT-bag model are employed to examine properties of hadron-(strange) quark hybrid stars. The hadron- (strange) quark hybrid stars become more stable at high densities compared to pure hadronic and pure strange quark stars.
Keywords:
Nonlinear s-w-r Mean-Field, Hyperon Onset Densities, Hyperon Coupling Ratios, Hadron-Quark Hybrid Stars
Subject Areas: Nuclear Physics, Nuclear Astrophysics, Many-Body Theory

1. Introduction
The symmetric nuclear matter is a self-bound matter whose binding energy exhibits a characteristic concave curve at saturation density, where pressure of nuclear matter vanishes . It has been known as a constraint to examine self-consistency to nuclear many-body approximations [1] - [3] . The self-consistency has been fundamental for many-body approximations in terms of Landau’s Fermi-liquid theory [4] - [6] , Kadanoff-Baym’s theory of conserving approximations [7] - [9] and the density functional theory [10] - [12] . The relativistic, field- theoretical, linear s-w mean-field approximations that maintain conditions of conserving approximations have been applied to finite nuclei, nuclear matter and neutron stars [13] [14] . These nuclear mean-field approximations reveal an important relation among self-consistent single particle energy, energy density and particle density, which is denoted as thermodynamic consistency [15] [16] . The conserving nonlinear s-w-r mean-field approximation which maintains thermodynamic consistency has been applied to investigate density-dependent correlations among properties of nuclear, neutron and hyperonic matter [17] - [19] . Thermodynamic consistency is important to derive consistent results for high energy and high density phenomena, such as heavy-ion collision, hypernuclei-formation experiments [20] and astrophysical phenomena [21] - [24] .
. It has been known as a constraint to examine self-consistency to nuclear many-body approximations [1] - [3] . The self-consistency has been fundamental for many-body approximations in terms of Landau’s Fermi-liquid theory [4] - [6] , Kadanoff-Baym’s theory of conserving approximations [7] - [9] and the density functional theory [10] - [12] . The relativistic, field- theoretical, linear s-w mean-field approximations that maintain conditions of conserving approximations have been applied to finite nuclei, nuclear matter and neutron stars [13] [14] . These nuclear mean-field approximations reveal an important relation among self-consistent single particle energy, energy density and particle density, which is denoted as thermodynamic consistency [15] [16] . The conserving nonlinear s-w-r mean-field approximation which maintains thermodynamic consistency has been applied to investigate density-dependent correlations among properties of nuclear, neutron and hyperonic matter [17] - [19] . Thermodynamic consistency is important to derive consistent results for high energy and high density phenomena, such as heavy-ion collision, hypernuclei-formation experiments [20] and astrophysical phenomena [21] - [24] .
The nonlinear s-w-r mean-field approximation has several nonlinear coefficients whose values are determined by reproducing binding energy, symmetry energy and simultaneously searching the minimum value of incompressibility at saturation density, as well as reproducing a maximum mass of neutron stars at high density.
The binding energy at saturation is taken as −15.75 MeV at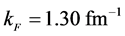 ,
, 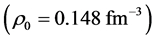 with the symmetry energy,
with the symmetry energy,  in the current calculation [13] . The values of nonlinear coefficients which will produce effective masses of hadrons
in the current calculation [13] . The values of nonlinear coefficients which will produce effective masses of hadrons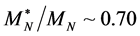 ,
,  ,
,  and incompressibility,
and incompressibility, 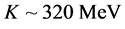 , with symmetry energy
, with symmetry energy , the maximum mass of neutron stars in b-equilibrium matter [23] ,
, the maximum mass of neutron stars in b-equilibrium matter [23] ,  (the solar mass:
(the solar mass: ), are found reasonable in the nonlinear s-w-r Hartree approximation [18] [19] .
), are found reasonable in the nonlinear s-w-r Hartree approximation [18] [19] .
The maximum masses of neutron stars are expected to be below 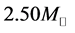 [25] , or
[25] , or  [26] , which depend on the hadronic equation of state (EOS) for isospin asymmetric, hyperonic matter in the density range,
[26] , which depend on the hadronic equation of state (EOS) for isospin asymmetric, hyperonic matter in the density range,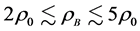 . The hadronic liquid-gas phase transition at the surface of neutron stars and determination of the radius of smeared, gas-phase surface are not directly relevant to properties of hadronic matter and maximum masses of neutron stars. Hence, significant contributions to properties of neutron stars (mass, radius, moment of inertia…) come from hadronic EOS. The gas-phase equation of state which may exist on the surface of neutron stars produces negligible corrections and it is not relevant in the current hadronic analysis.
. The hadronic liquid-gas phase transition at the surface of neutron stars and determination of the radius of smeared, gas-phase surface are not directly relevant to properties of hadronic matter and maximum masses of neutron stars. Hence, significant contributions to properties of neutron stars (mass, radius, moment of inertia…) come from hadronic EOS. The gas-phase equation of state which may exist on the surface of neutron stars produces negligible corrections and it is not relevant in the current hadronic analysis.
The nonlinear interactions exhibit significant density-dependent effects on incompressibility, K, and symmetry energy,  , in high densities; these Fermi liquid properties monotonically increase about saturation density, but they are piecewise continuously softened at an hyperon onset density. These phenomena of piecewise continuous change of Fermi-liquid properties will be important for the analysis of Landau parameters, heavy-
, in high densities; these Fermi liquid properties monotonically increase about saturation density, but they are piecewise continuously softened at an hyperon onset density. These phenomena of piecewise continuous change of Fermi-liquid properties will be important for the analysis of Landau parameters, heavy-
ion collision, high energy and high density experiments. At a hyperon onset density from  to
to

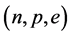
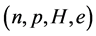
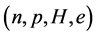
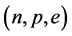
and slow increase of Fermi energies appear whenever hyperons are generated, resulting in a softer equation of state and discontinuous changes of K and
Since the hyperon-onset confines Fermi-energies of baryons as explained above, single and double hyperon generations exhibit different density-dependent phenomena. For example, the 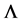
as in 
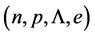
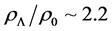
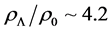
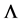
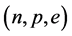
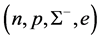

onset-density of a hyperon is pushed up to a higher density, which is denoted as the push-up phenomena of hyperon onset-densities in many-fold hyperon generations [18] . Because of the push-up phenomena of the hyperon onset density, we have found that hyperon generations are confined at high densities and hyperons relevant to calculations of neutron stars are 
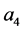
Density-dependent effective masses and effective coupling constants, saturation properties for nucleons and hyperons are discussed in the nonlinear s-w-r mean-field approximation [18] [19] . The results shown that: 1) coupling constants of hyperons are related to those of nucleons by effective masses, effective coupling constants, binding energy at onset-density of respective hyperons. Hence, binding energies of symmetric nuclear matter and hyperon matter are self-consistently related to each other. 2) Self-consistency and density-dependent interactions may restrict hyperon generations at low densities, resulting in the push-up phenomena of hyperon onset densities. The suppression of hyperon generations is also discussed in different calculations [27] - [29] . 3) Coupling ratios of hyperons are expected to be
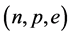
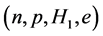
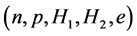
The conserving nonlinear s-w-r mean-field approximation [17] - [19] and quark-based effective nuclear models [34] [35] have been applied to finite nuclei, nuclear and isospin asymmetric, high-density matter. We have compared hyperon coupling constants required by the nonlinear s-w-r mean-field model with those required by SU(6) quark model for the vector coupling constants [36] [37] . The hyperon coupling constants required by hadronic and SU(6) quark models exhibit quite different results for effective masses, binding energies of hyperons [18] [19] and properties of hadron-quark hybrid stars. The coupling ratios required by SU(6) quark model cannot reproduce hyperon saturation properties, which will be discussed in terms of conditions of thermodynamic consistency in the Section 4. The analysis of discrepancies of predictions by hadronic and quark-based models may provide us with insight for constructing self-consistent nuclear many-body approximations [14] - [19] . The effective masses of hyperons depend on coupling ratios (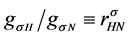
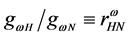

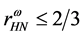
In the hadronic mean-field approximation, 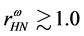
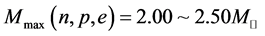
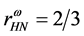
The density-dependent many-body effects produced by the conserving nonlinear s-w-r mean-field approximation should be compared to chiral hadronic mean-filed approximations [38] - [41] . The effective quark-based chiral Lagrangian approach suggests that the appropriate in-medium scaling law,
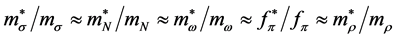
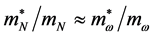
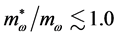
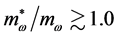

significantly different from nonlinear mean-field approximations, since self-consistency of hadronic mean-field approximation demands 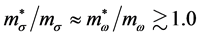
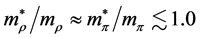
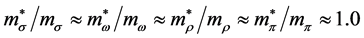
We have applied the nonlinear s-w-r mean-field approximation and MIT-bag model upon hadron-quark hybrid stars [23] [45] . The numerical analysis exhibits new results that the hadron-(strange) quark hybrid stars are more stable in high density than pure-hadronic and pure-strange quark stars. It suggests a relation between bag constant and QCD strong coupling constant, (B,
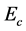
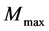
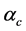
Self-consistent relations among saturation properties of nucleons and hyperons are briefly reviewed in Section 2. Quantitative numerical calculations for effective masses, onset densities and conditions of hyperon saturation are discussed in the articles [18] [19] . The MIT-bag quark matter and vacuum fluctuation correction to nonlinear mean-field approximation are explained in Section 3. Results of pure hadron and hadron-strange quark hybrid stars are discussed in Section 4; concluding remarks are in Section 5.
2. Self-Consistent Effective Masses and Coupling Constants in the Nonlinear s-w-r Mean-Field Approximation
The hadronic Lagrangian with nonlinear s-w-r interactions which yields density-dependent effective masses and coupling constants is given by [17] ,
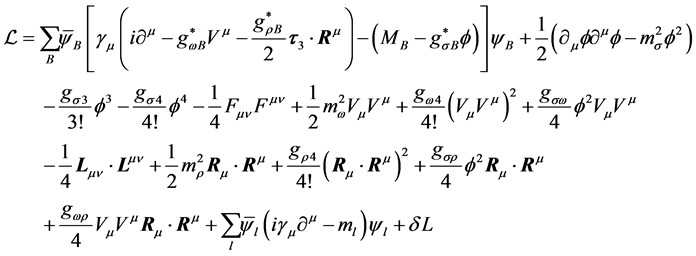
where 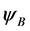
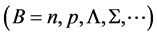
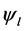
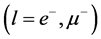
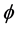

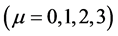
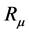
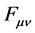
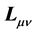
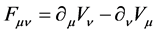
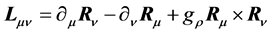
The coupled nonlinear quantum-field Lagrangian (2.1) is interpreted as baryon quantum-field Lagrangian in mean fields of mesons [13] . All dynamics generated by baryon fields are mediated by mean-fields of mesons which will be self-consistently defined in an approximation. The effective coupling constants, 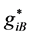
Meson-fields operators are replaced by mean-fields denoted by
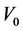
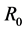
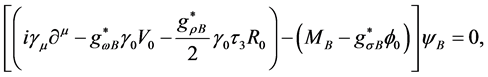
where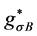
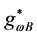
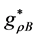
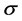
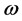

The equations of motion for mesons are given by,
where 
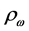
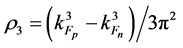
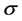
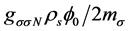
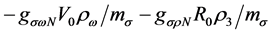
The introduction of nonlinear 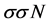
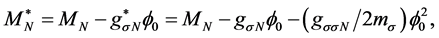
and effective masses of nucleons and hyperons are related to each other as,

The total scalar source is obtained as,
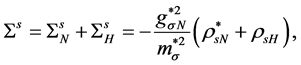
where the scalar sources are respectively given by
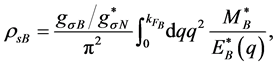
and 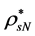
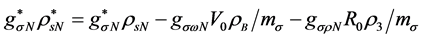
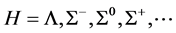
The w-meson and r-meson contributions to self-energies are given by
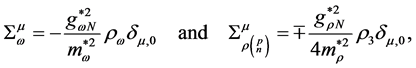
where the baryon-hyperon density, 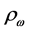

and 

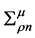

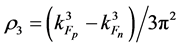
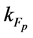

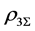
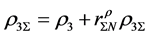

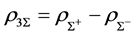
Thermodynamically consistent effective masses of mesons compatible with effective coupling constants (2.3) are required to be:
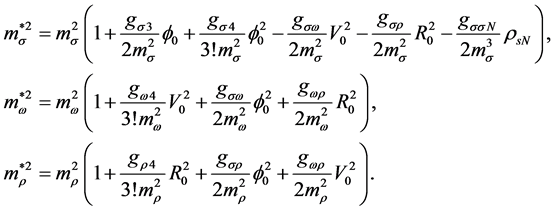
Since effective masses of mesons and coupling constants depend on mean fields of mesons, they are density- dependent through meson fields. Note that the effective mass of s-meson depends on the 
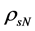
The energy density, pressure of isospin-symmetric, asymmetric and charge-neutral hadronic matter are calculated by way of energy-momentum tensor, resulting in:
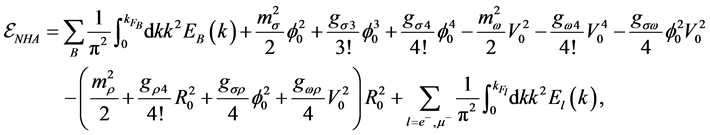
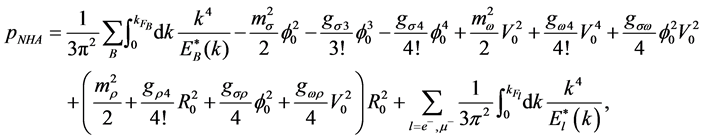
where 
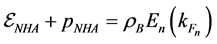


The functional derivative of energy density, 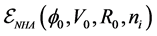
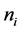
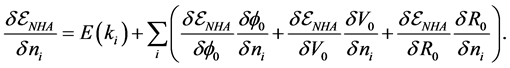
Thermodynamic consistency requires: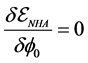
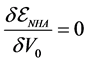
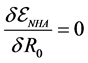
prove that the self-energies calculated by propagators and the conditions of conserving approximations become equivalent, only if the effective masses and effective coupling constants of mesons are given by (2.3) and (2.11) [17] - [19] .
In order to start self-consistent hadronic matter calculations, nonlinear coupling constants, 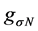
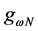
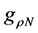
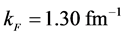
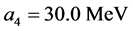
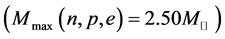

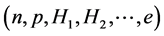
3. The Nonlinear s-w-r Mean-Field Approximation with Vacuum Fluctuation Correction (VFC)
We have included vacuum fluctuation correction (VFC) into the nonlinear s-w-r mean-field approximation and applied the EOS with or without VFC to hadronic stars and hadron-quark hybrid stars. The EOSs for hadrons with VFC and quark matter generated by MIT-bag model are briefly discussed; based on the formalism, the pure hadronic and quark stars, stability of hadron-quark stars, are discussed in Section 4. The vacuum fluctuation corrections are explicitly performed with counter terms required by power-counting and the method of dimensional regularization [13] .
The self-energies with VFC in the conserving nonlinear s-w-r approximation are given with (2.7) by,

where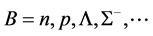

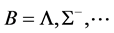

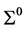
The differences of VFC (3.1) given by the linear 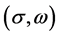
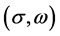
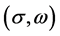
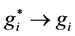
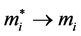
The energy density with VFC is obtained as,

Then, the total energy density is given with Equation (2.12) as,

The self-energies and pressure are also evaluated by dimensional regularization and thermodynamic consistency can be proved including VFC. As discussed in Section 2, all coupling constants have to be evaluated by maintaining properties at nuclear matter saturation, searching the minimum value of incompressibility. Incompressibility is 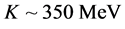
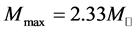
Hadronic degrees of freedom give the most convenient description of EOS around nuclear matter saturation density, and at high densities where asymptotic freedom sets in, a quark description would be more natural. Hence, the hadronic equations of state 
The energy density and pressure for quark matter given by MIT-bag model are obtained [45] - [47] :


where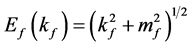
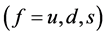
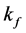
tum of flavor f. The energy density and pressure with the following given baryon density, charge neutrality and phase equilibrium conditions:
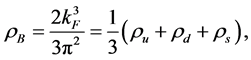
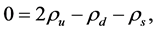
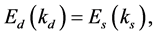
determine (u, d, s)-quark matter uniquely (note: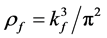
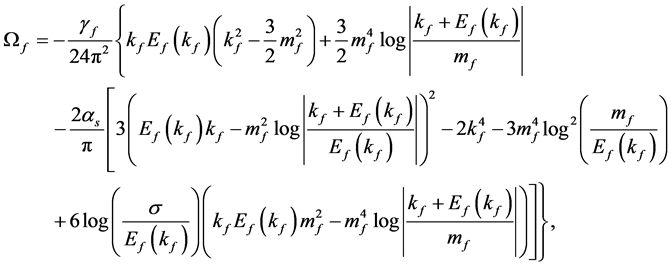
where 

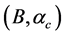
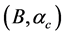
The energy density and pressure are now expressed as,
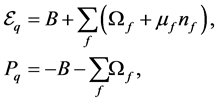
where 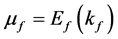
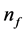
4. The Properties of Hadronic and Hadron-Quark Hybrid Stars
We have applied the conserving nonlinear s-w-r mean-field approximation to examine properties of hadronic neutron stars and hadron-quark hybrid stars. The properties of pure hadronic stars are produced by employing hadronic equations of state, phase transition conditions, coupling ratios and TOV equation.
The masses v.s. central densities of hadronic stars produced by equations of state for 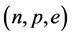
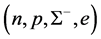
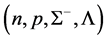
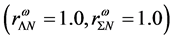
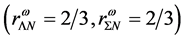
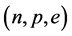
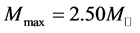
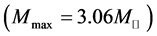
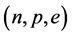
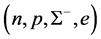
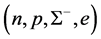
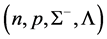
The EOS of hadronic matter with 
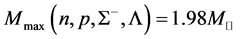
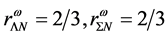
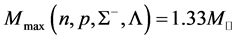

The properties of pure hadronic stars including VFC are shown in Figure 2(a) and Figure 2(b). The VFC effects are not so significant both in low and high densities compared with those of nonlinear many-body interactions. The difference of pressure and energy density in phase transition region is small (see arrows in Figure 2(a) and Figure 2(b)), which makes EOS smooth (see also Figure 1(a) and Figure 1(b)). Notice that the
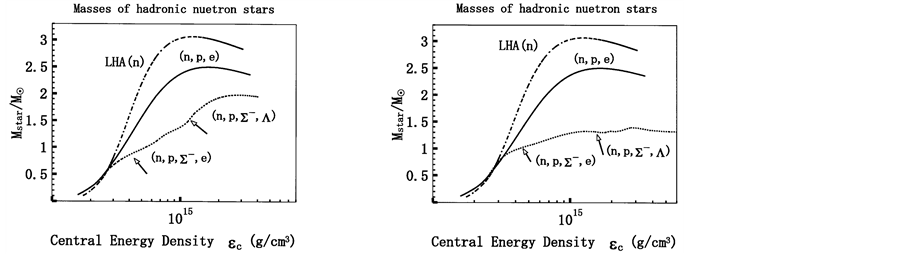
Figure 1. (a) Masses of hadronic neutron stars. Pure-neutron matter in linear s-w: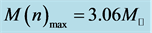
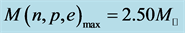
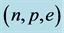

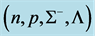
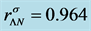
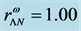
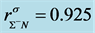
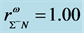


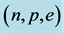
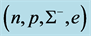
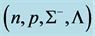



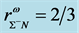
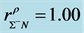

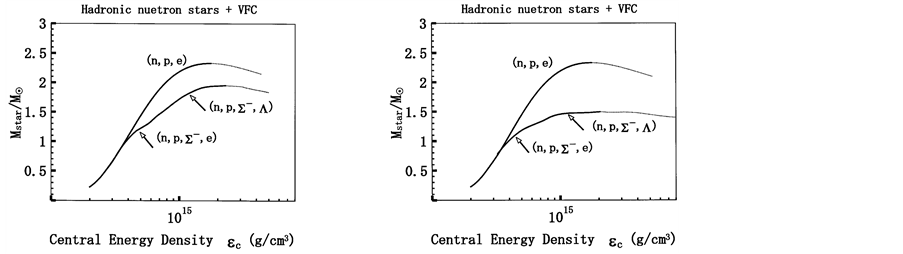
Figure 2. (a) Hadronic neutron stars with VFC. 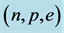

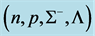
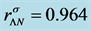
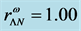
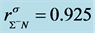
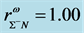
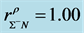
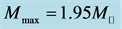
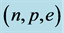


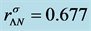

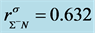
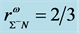
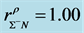

stable hadronic stars with 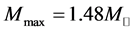
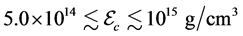
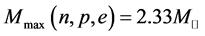
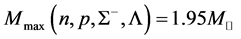
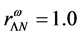
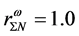

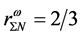
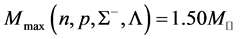
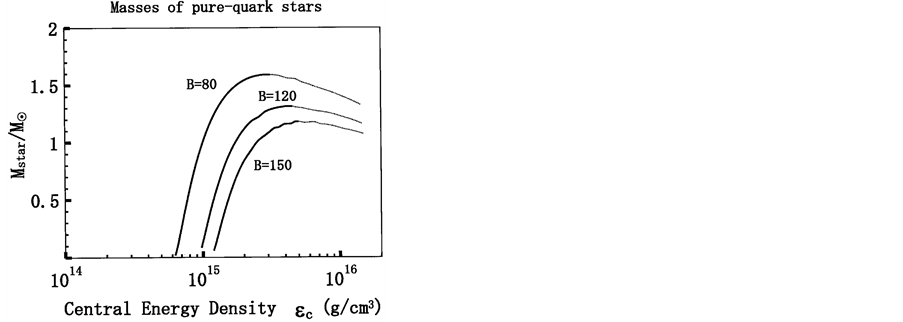
The EOS of pure-quark matter is used to calculate masses of pure-quark stars, which is shown in Figure 3. The bag constant should be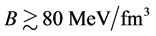
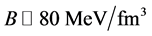
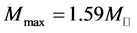
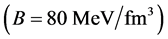


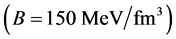
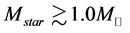
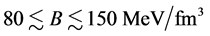
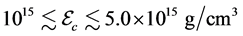
The stable hadronic neutron stars with VFC and pure quark stars are shown in Figure 4, in order to remark energy-density regions of stable stars, respectively. The results of hadronic and quark stars in Figure 4 suggest that hadron-quark hybrid stars be possible about the central energy density, 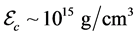

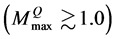
We assumed the first order hadron-quark phase transition, and solved phase transition conditions for chemical potential and pressure: 


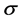
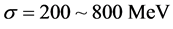
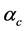
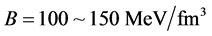
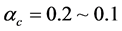
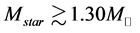

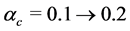
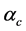

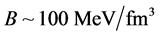
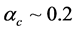
Figure 3. Masses of pure-quark stars with
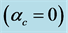
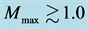
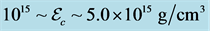
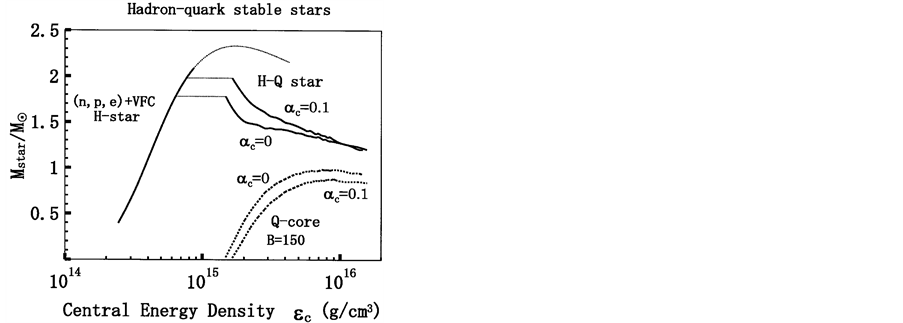
Figure 4. Hadron stars with VFC and pure-quark stars. The stable hadronic stars are in
Figure 5. Hadron-quark stars based on isospin asymmetric (n, p, e) + VFC matter. Note that the quark-core of H-Q stars is stable.
and (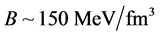
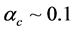

Since H-Q stars are 2-phase compact stars (quark phase for star’s core and hadron phase for a mantle), the stability of H-Q stars should be reconsidered. The stability of pure hadronic and quark matter is examined respectively by the condition: 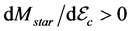
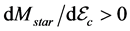
The hadron-quark stars in Figure 5 show that the stable hadronic stars 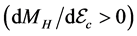
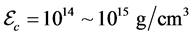
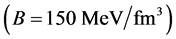
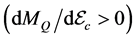
develop. Therefore, it suggests that the H-Q star be stable, although the total mass of the star becomes smaller. Moreover, by comparing the stable energy densities of quark phase in Figure 4 with those of H-Q stars, it is found that the central energy density of stable H-Q stars is more extended for higher densities than that of single phase stars. It suggests that compact stars consisting of a mantle and a high density core be more stable than stars in a homogeneous single phase structure [47] [49] . When the QCD coupling constant, 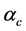
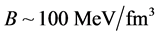
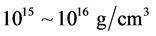
The H-Q stars calculated with the EOS for 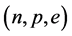
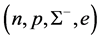
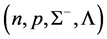
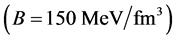
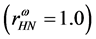
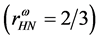

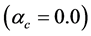
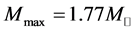
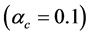
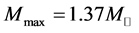
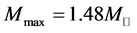
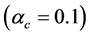
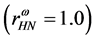
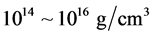
In cases of the softer hadronic EOS in Figure 6(b) 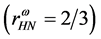
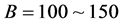
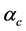
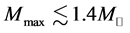
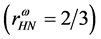
If QCD coupling constant is set large, 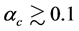
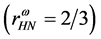
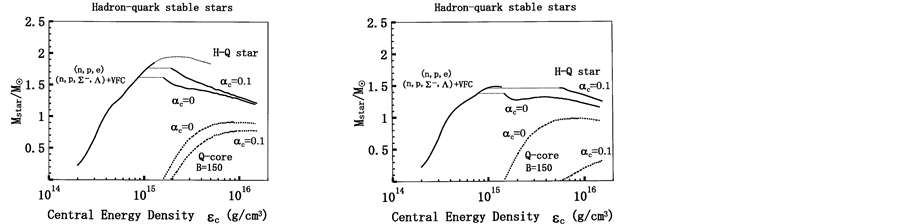
Figure 6. (a) Hadron-quark stars based on 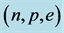
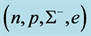
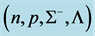
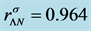
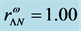
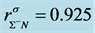
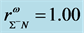
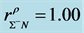
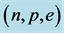
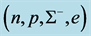
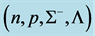
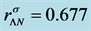
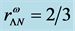

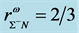

hadronic and quark matter, the coupling constants for hadrons (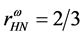
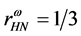
5. Concluding Remarks
The quantum hadrodynamics (QHD) and mean-field approximations are useful for describing hadronic many- body systems at large distances, but they must ultimately break down at short distances where QCD is valid; hence, it is interesting to investigate how properties of hadron and quark dynamics will interconnect and influence each other dynamically [13] [14] . We applied the conserving nonlinear s-w-r mean-field approximation to study self-consistent, density-dependent interactions of hadrons and examined hadronic dynamics by employing coupling constants required from the QCD degrees of freedom. Discrepancies between hadronic and QCD predictions are explicitly shown by calculating masses of high density compact stars. The analysis is also applied to properties of nuclear matter, such as effective masses and effective coupling constants of nucleons, incompressibility and symmetry energy, saturation properties of hyperon binding energies [24] . The results may help understand predictions by effective hadronic and quark models as well as efficiencies and interrelations between models.
As saturation properties of symmetric nuclear matter are self-consistently related to those of hyperons, reproducing saturation properties of hyperons should be one of fundamental problems of nuclear many-body approximations. Although more quantitative and model-independent analyses are needed, it is concluded that hyperon coupling ratios required by SU(6) quark model for the vector coupling constants [36] [37] are not appropriate in order to generate saturation properties of hyperons. The coupling ratios of hyperons, 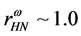
Heavy-ion collision experiments as well as neutron stars are useful to examine validity of quark and hadronic models [50] [51] , since conditions of hadron-quark phase transition depend on both equations of state for hadronic and quark matter. The appropriate values of 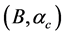
g/cm3. In the range of energy density, pure-hadron stars are less than


existing high density compact stars are more likely to be regarded as hadron-quark stars rather than pure-hadron and pure-quark stars. These results should be further studied quantitatively by empirical data and effective theories of hadrons.
It is noteworthy that density-dependent many-body effects simulated by nonlinear s-w-r interactions are more important than those of vacuum fluctuation corrections (VFC). The contributions of VFC should be investigated further in more complicated nonlinear s-w-r HF, BHF approximations in order to study density-depen- dent and VFC corrections quantitatively. The role of chiral symmetry in hadronic models should be examined by extending the current nonlinear s-w-r mean-field approximation by including p-meson, which would help understand physical meaning and significance of chirality for hadronic and quark models.
Cite this paper
Schun T. Uechi,Hiroshi Uechi, (2015) Hardon-Quark Hybrid Stars Constructed by the Nonlinear σ-ω-ρ Mean-Field Model and MIT-Bag Model. Open Access Library Journal,02,1-16. doi: 10.4236/oalib.1102012
References
- 1. Day, B.D. (1978) Current State of Nuclear Matter Calculations. Reviews of Modern Physics, 50, 495-521.
http://dx.doi.org/10.1103/RevModPhys.50.495 - 2. Hugenholtz, N.M. and Van Hove, L. (1958) A Theorem on the Single Particle Energy in a Fermi Gas with Interaction. Physica, 24, 363-376.
http://dx.doi.org/10.1016/S0031-8914(58)95281-9 - 3. Brueckner, K.A. and Levinson, C.A. (1955) Approximate Reduction of the Many-Body Problem for Strongly Interacting Particles to a Problem of Self-Consistent Fields. Physical Review, 97, 1344-1352.
http://dx.doi.org/10.1103/PhysRev.97.1344
Brueckner, K.A. (1958) Single-Particle Energy and Effective Mass and the Binding Energy of Many-Body Systems, Single Particle Energies in the Theory of Nuclear Matter. Physical Review, 110, 597-600.
http://dx.doi.org/10.1103/PhysRev.110.597
Brueckner, K.A. and Goldman, D.T. (1960) Single Particle Energies in the Theory of Nuclear Matter. Physical Review, 117, 207-213.
http://dx.doi.org/10.1103/PhysRev.117.207
Brueckner, K.A., Gammel, J.L. and Kubis, J.T. (1960) Calculation of Single-Particle Energies in the Theory of Nuclear Matter. Physical Review, 118, 1438-1441.
http://dx.doi.org/10.1103/PhysRev.118.1438 - 4. Landau, L.D. (1956) Theory of Fermi-Liquids. Soviet Physics JETP-USSR, 3, 920-925.
Landau, L.D. (1957) Oscillations in a Fermi-Liquid. Soviet Physics JETP-USSR, 5, 101-108. - 5. Pines, D. and Nozières, P. (1966) The Theory of Quantum Liquids. Addison-Wesley, Boston.
- 6. Nozières, P. (1964) Theory of Interacting Fermi Systems. Perseus Publishing, New York.
- 7. Baym, G. and Kadanoff, L.P. (1961) Conservation Laws and Correlation Functions. Physical Review, 124, 287-299.
http://dx.doi.org/10.1103/PhysRev.124.287
Baym, G. (1962) Self-Consistent Approximations in Many-Body Systems. Physical Review, 127, 1391-1401.
http://dx.doi.org/10.1103/PhysRev.127.1391 - 8. Takada, Y. (1995) Exact Self-Energy of the Many-Body Problem from Conserving Approximations. Physical Review, B52, 12708-12719.
http://dx.doi.org/10.1103/PhysRevB.52.12708 - 9. Bonitz, M., Nareyka, R. and Semkat, D., Eds. (2000) Progress in Nonequilibrium Green’s Functions, Progress in Nonequilibrium Green’s Functions II. World Scientific, Singapore.
- 10. Kohn, W. and Sham, L.J. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, A1133.
http://dx.doi.org/10.1103/physrev.140.a1133 - 11. Kohn, W. (1999) Nobel Lecture: Electronic Structure of Matter-Wave Functions and Density Functional. Reviews of Modern Physics, 71, 1253-1266.
http://dx.doi.org/10.1103/RevModPhys.71.1253 - 12. Uechi, H. (2004) The Theory of Conserving Approximations and the Density Functional Theory in Approximations for Nuclear Matter. Progress of Theoretical Physics, 111, 525-543.
http://dx.doi.org/10.1143/PTP.111.525 - 13. Serot, B.D. and Walecka, J.D. (1986) Advances in Nuclear Physics. Vol. 16, Negele, J.W. and Vogt, E., Eds., Plenum, New York.
- 14. Serot, B.D. (1992) Quantum Hadrodynamics. Reports on Progress in Physics, 55, 1855-1946.
http://dx.doi.org/10.1088/0034-4885/55/11/001 - 15. Uechi, H. (1989) Fermi-Liquid Properties of Nuclear Matter in a Dirac-Hartree-Fock Approximation. Nuclear Physics A, 501, 813-834.
http://dx.doi.org/10.1016/0375-9474(89)90162-0
Uechi, H. (1992) Landau Fermi-Liquid Theory and Approximations in the Quantum Hadrodynamical Model. Nuclear Physics A, 541, 397-412.
http://dx.doi.org/10.1016/0375-9474(92)90183-K - 16. Furnstahl, R.J. and Serot, B.D. (1991) Covariant Feynman Rules at Finite Temperature: Time-Path Formulation. Physical Review C, 44, 2141-2174.
http://dx.doi.org/10.1103/PhysRevC.44.2141
Furnstahl, R.J. and Serot, B.D. (1990) Covariant Mean-Field Calculations of Finite-Temperature Nuclear Matter. Physical Review C, 41, 262-279.
http://dx.doi.org/10.1103/PhysRevC.41.262 - 17. Uechi, H. (2006) Properties of Nuclear and Neutron Matter in a Nonlinear σ-ω-ρ Mean-Field Approximation with Self- and Mixed-Interactions. Nuclear Physics A, 780, 247-273.
http://dx.doi.org/10.1016/j.nuclphysa.2006.10.015
Uechi, H. (2008) Density-Dependent Correlations between Properties of Nuclear Matter and Neutron Stars in a Nonlinear σ-ω-ρ Mean-Field Approximation. Nuclear Physics A, 799, 181-209.
http://dx.doi.org/10.1016/j.nuclphysa.2007.11.003 - 18. Uechi, S.T. and Uechi, H. (2009) The Density-Dependent Correlations among Observables in Nuclear Matter and Hyperon-Rich Neutron Stars. Advances in High Energy Physics, 2009, Article ID: 640919.
http://dx.doi.org/10.1155/2009/640919 - 19. Uechi, H. and Uechi, S.T. (2009) Saturation Properties and Density-Dependent Interactions among Nuclear and Hyperon Matter. The Open Nuclear & Particle Physics Journal, 2, 47-60.
http://dx.doi.org/10.2174/1874415X00902010047 - 20. Botvina, A.S. and Pochodzalla, J. (2007) Production of Hypernuclei in Multifragmentation of Nuclear Spectator Matter. Physical Review C, 76, Article ID: 024909.
http://dx.doi.org/10.1103/PhysRevC.76.024909 - 21. Misner, C.W., Thorne, K.S. and Wheeler, J.W. (1973) Gravitation. W. H. Freeman and Company, New York.
- 22. Arnett, D. (1996) Supernovae and Nucleosynthesis. Princeton University Press, Princeton.
- 23. Glendenning, N.K. (2000) Compact Stars. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-1212-6 - 24. Uechi, H., Uechi, S.T. and Serot, B.D., Eds. (2012) Neutron Stars: The Aspect of High Density Matter, Equations of State and Related Observables. Nova Science Publisher, New York.
- 25. Akmal, A., Pandharipande, V.R. and Ravenhall, D.G. (1998) Equation of State of Nucleon Matter and Neutron Star Structure. Physical Review C, 58, 1804-1828.
http://dx.doi.org/10.1103/PhysRevC.58.1804 - 26. Lattimer, J.M. and Prakash, M. (2007) Neutron Star Observations: Prognosis for Equation of State Constraints. Physics Reports, 442, 109-165.
http://dx.doi.org/10.1016/j.physrep.2007.02.003 - 27. Vidaña, I., Polls, A., Ramos, A., Engvik, L. and Hjorth-Jensen, M. (2000) Hyperon-Hyperon Interactions and Properties of Neutron Star Matter. Physical Review C, 62, Article ID: 035801.
http://dx.doi.org/10.1103/PhysRevC.62.035801 - 28. Baldo, M., Burgio, G.F. and Schulze, H.J. (2000) Hyperon Stars in the Brueckner-Bethe-Goldstone Theory. Physical Review C, 61, Article ID: 055801.
http://dx.doi.org/10.1103/PhysRevC.61.055801 - 29. Maruyama, T., Chiba, S., Schulze, H.J. and Tatsumi, T. (2007) Hadron-Quark Mixed Phase in Hyperon Stars. Physical Review D, 76, Article ID: 123015.
http://dx.doi.org/10.1103/PhysRevD.76.123015 - 30. Uechi, H. (2008) Correlations between Saturation Properties of Isospin Symmetric and Asymmetric Nuclear Matter in a Nonlinear σ-ω-ρ Mean-Field Approximation. Advanced Studies in Theoretical Physics, 2, 519-548.
- 31. Gal, A. (2003) To Bind or Not to Bind: ΛΛ Hypernuclei and Ξ Hyperons. Nuclear Physics A, 721, C945-C950.
http://dx.doi.org/10.1016/S0375-9474(03)01248-X - 32. Glendenning, N.K., Von-Eiff, D., Haft, M., Lenske, H. and Weigel, M.K. (1993) Relativistic Mean-Field Calculations of Λ and Σ Hypernuclei. Physical Review C, 48, 889-895.
http://dx.doi.org/10.1103/PhysRevC.48.889 - 33. Bellac, M.L., Mortessagne, F. and Bartrouni, G.G. (2004) Equilibrium and Non-Equilibrium Statistical Thermodynamics. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511606571 - 34. Gelmini, G. and Ritzi, B. (1995) Chiral Effective Lagrangian Description of Bulk Nuclear Matter. Physics Letters B, 357, 431-434.
http://dx.doi.org/10.1016/0370-2693(95)00924-A - 35. Huguet, R., Caillon, J.C. and Labarsouque, J. (2007) Saturation Properties of Nuclear Matter in a Relativistic Mean Field Model Constrained by the Quark Dynamics. Nuclear Physics A, 781, 448-458.
http://dx.doi.org/10.1016/j.nuclphysa.2006.11.046 - 36. Schaffner, J. and Mishustin, I.N. (1996) Hyperon-Rich Matter in Neutron Stars. Physical Review C, 53, 1416-1429.
http://dx.doi.org/10.1103/PhysRevC.53.1416 - 37. Shao, G.-Y. and Liu, Y.-X. (2009) Influence of the σ-ω Meson Interaction on Neutron Star Matter. Physical Review C, 79, Article ID: 025804.
http://dx.doi.org/10.1103/PhysRevC.79.025804 - 38. Furnstahl, R.J., Serot, B.D. and Tang, H.-B. (1997) A Chiral Effective Lagrangian for Nuclei. Nuclear Physics A, 615, 441-482.
http://dx.doi.org/10.1016/S0375-9474(96)00472-1 - 39. McIntire, J., Hu, Y. and Serot, B.D. (2007) Loop Corrections and Naturalness in a Chiral Effective Field Theory. Nuclear Physics A, 794, 166-186.
http://dx.doi.org/10.1016/j.nuclphysa.2007.08.008 - 40. Walecka, J.D. (1995) Theoretical Nuclear and Subnuclear Physics. Oxford University Press, Oxford.
- 41. Jha, T.K. and Mishra, H. (2008) Constraints on Nuclear Matter Parameters of an Effective Chiral Model. Physical Review C, 78, Article ID: 065802.
http://dx.doi.org/10.1103/PhysRevC.78.065802 - 42. Brown, G.E. and Rho, M. (1991) Scaling Effective Lagrangians in a Dense Medium. Physical Review Letters, 66, 2720-2723.
http://dx.doi.org/10.1103/PhysRevLett.66.2720 - 43. Chiapparini, M., Bracco, M.E., Delfino, A., Malheiro, M., Menezes, D.P. and Providência, C. (2009) Hadron Production in Non-Linear Relativistic Mean Field Models. Nuclear Physics A, 826, 178-189.
http://dx.doi.org/10.1016/j.nuclphysa.2009.05.002 - 44. Uechi, H. and Uechi, S.T. (2008) Meeting Abstract. The Annual Meeting of Japan Physical Society, 63, Part 1, 49.
- 45. Serot, B.D. and Uechi, H. (1987) Neutron Stars in Relativistic Hadron-Quark Models. Annals of Physics, 179, 272-293.
http://dx.doi.org/10.1016/0003-4916(87)90137-0 - 46. Chodos, A., Jaffe, R.L., Johnson, K., Thorn, C.B. and Weisskopf, V.F. (1974) New Extended Model of Hadrons. Physical Review D, 9, 3471-3495.
http://dx.doi.org/10.1103/PhysRevD.9.3471 - 47. Farhi, E. and Jaffe, R.L. (1984) Strange Matter. Physical Review D, 30, 2379-2390.
http://dx.doi.org/10.1103/PhysRevD.30.2379 - 48. Shapiro, S.L. and Teukolsky, S.A. (1983) Black Holes, White Dwarfs, and Neutron Stars. John Wiley & Sons Inc., Hoboken.
http://dx.doi.org/10.1002/9783527617661 - 49. Witten, E. (1984) Cosmic Separation of Phases. Physical Review D, 30, 272-285.
http://dx.doi.org/10.1103/PhysRevD.30.272 - 50. Dexheimer, V.A. and Schramm, S. (2009) Neutron Stars as a Probe for Dense Matter. Nuclear Physics A, 827, 579c-581c.
http://dx.doi.org/10.1016/j.nuclphysa.2009.05.127 - 51. Bombaci, I., Logoteta, D., Panda, P.K., Providência, C. and Vidaña, I. (2009) Quark Matter Nucleation in Hot Hadronic Matter. Physics Letters B, 680, 448-452.
http://dx.doi.org/10.1016/j.physletb.2009.09.039