Received 28 October 2015; accepted 12 November 2015; published 18 November 2015

ABSTRACT

Adsorption kinetics and mechanism of Cypermethrin (CY) and Dichlorovos (DI) on activated carbons of oil bean seed shell (OBSS), unripe plantain peel (UPP) and castor bean seed shell (CBSS) systems have been studied. The equilibrium adsorption isotherms were modelled by Freunlich, Langmuir and Langmuir-Freunlich (LF) models. Adsorption isotherms of various systems were best described by Langmuir-Freunlich (LF). Mixed 1,2 order equation (MOE), integrated kinetic Langmuir (IKL), pseudo second order equation (PSOE), fractal-like mixed 1,2 order equation (F-MOE), and Boyd and Webbers models were compared and adopted in the analysis of the kinetic data. The models represented different uptake reduction rate of CY and DI by various adsorption systems. F-MOE, IKL and MOE models were in agreement with CY/OBSS, CY/UPP and CY/CBSS system data respectively, hence the conforming models, whereas IKL, MOE and PSOE were the conforming models for DI/OBSS, DI/UPP and DI/CBSS adsorption data systems, respectively. The two diffusion models (Boyd and Webbers) applied confirmed film diffusion pattern as prevailing transportation pathway for CY and DI onto the adsorbents.

Keywords:

Adsorption Kinetic Models, Diffusion, Dichlorovos, Cypermethrin, Equilibrium, Isotherms

Subject Areas: Chemical Engineering & Technology, Environmental Sciences

1. Introduction

Pollution by herbicides, pesticides and other agro-chemical applications meant to boost food production has been traced to major cancer related health issues in human (International Agency for Research on Cancer (IARC)). A good amount of agro-chemicals get to natural environment because of high mobility and recalcitrant tendency associated with them. Some pesticides are weakly held to the soil hence easily dissolved in water with attendant potential to contaminate both surface and ground water [1] [2] . On the other hand, certain pesticides are persistence in water and soil environments, thus making them less vulnerable to solvation with water. Thus, several removal methods such as reverse osmosis, coagulation etc. have been applied to remove the pesticides/ herbicides from polluted water. Recent removal techniques such as adsorption have also been adopted with synthetic adsorbent media to treat polluted water of pesticides. All these techniques yielded impressive results but they were expensive hence not easily affordable. Other researchers have also applied natural adsorbent media such as wood activated charcoal and other activated adsorbents of agricultural waste origin [3] - [6] to remove herbicides (MCPA and 2,4-D), Methylene Blue, anionic dye Acidic 14 etc. with remarkable results.

Generally, principle of adsorption largely depends on a number of factors which include: physical and chemical properties of the pollutants and the physical properties of the adsorbents such as the surface area, bulk density, pore sizes, and pore distribution. Solubility levels of the pollutants in solution determine to a large extent its availability at precipitated form hence its capacity to adsorb in a solid phase. A pollutant which is sparingly soluble as a result of intermolecular bond formation existing between molecules, experiences weak salvation resulting to precipitation and eventual strong adsorption affinity to solid phase. Also, high molecular and density pollutants have the tendency for easy adsorption onto solid phase, especially graphene-like structure, because of low solubility characteristics of the pollutants. Adsorption of pollutant onto a solid phase is also a function of surface properties such as particle size and surface heterogeneity [7] - [10] .

1.1. Langmuir Kinetic Models

Data obtained from adsorption process are usually fit into kinetic models to establish the model(s) best describe(s) the adsorption behavior of the process. Giving the information from the literature, different equilibrium and kinetic models have been used to simulate experimental data got from adsorption processes. Most frequently used are Fraudlich, Langmuir, pseudo first and second order. Recently, mixed 1,2 order equation (MOE), generalized integrated kinetic Langmuir (GIKL), integrated kinetic Langmuir (IKL) and Langmuir-Freundlich (L-F) were introduced to represent the Langmuir Kinetic models. Most times, important adsorption systems are too complicated to model due to difficulty in acquiring good adsorption data. However, simple Langmuir kinetic models have been successful in describing such adsorption systems. Adsorption progress in a Langmuir kinetic adsorption system is expressed as follows

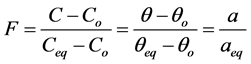(1)

where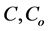, , 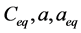and are concentration of solute in bulk solution after a time t, initial solute concentration in solution, solute concentration in solution at equilibrium, amount of solute on the solid phase (adsorbent), amount of solute on the solid phase at equilibrium adsorption coverage after a time, t and adsorption coverage at equilibrium respectively. The success of Langmuir Kinetic models in describing an adsorption system solely depends on Langmuir equilibrium batch factor [3] [9] expressed in Equation (2). Values of 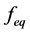determine the general kinetic behavior of an adsorption system.

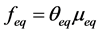(2)

where 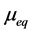is solute uptake at equilibrium and is expressed as

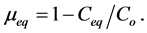(3)

Amount of solute adsorbed on the solid phase, (a) and relative adsorption coverage 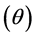are expressed in mass balanced equation associated with batch process as follows;

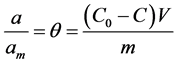(3a)

where and m are volume of the aqueous solution, adsorption capacity of adsorbents and mass of the solute (adsorbate) respectively?

1.2. Integrated Kinetic Langmuir (IKL)/General Integrated Kinetic Langmuir (gIKL)

As Equation (1) expresses adsorption progress, F, with respect to solute concentration, adsorption coverage and solute concentration on the solid phase (adsorbent), adsorption progress can as well be expressed with respect to solute uptake and equilibrium uptake as

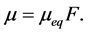(4)

Marczewski 2010 [11] put all these relationships together after observing the following boundary conditions;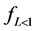, t = 0 and F = 0 to obtain generalized integrated kinetic Langmuir (gIKL) equation, expressed as

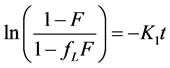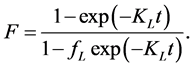and (5)

It is also imperative to mention that the generalized Langmuir batch equilibrium factor, establishes a link between gIKL and other models. For instance, gIKL (Equation (5)) can deviate to PSOE at

Also, at zero initial adsorption coverage (i.e.), and gIKL (Equation (5)) is regarded as Integrated kinetic Langmuir(IKL) and is presented as follows.

and (6)

represents the Langmuir equilibrium batch factor. The factor is a strong determinant to the behavior of langmuirian batch adsorption systems [9] [12] . We can obtain the standard pseudo second order from Equation (6) if and become equal to unity.

There are remarkable similarities between IKL and MOE. The two models share certain common properties such as first order kinetic rate constant, and contribution of second order kinetics,. These two constants must be equal to Langmuir batch equilibrium factor for MOE to fully function as Langmuir rate equation otherwise it behaves like every other empirical equation capable of describing non-Langmuirian adsorption systems [13] .

1.3. Pseudo-First, Second and MOE

Research has shown that adsorption systems well described by second order kinetics are more common than the ones described by the first Order Kinetics [14] [15] . Applications of these models depend on the amount of final solute uptake onto the adsorbent. It was observed that an adsorption process characterized by low adsorbate uptake is usually described by PFOE kinetic model whereas PSOE best describes an adsorption system which has large adsorbate uptake [16] . This could explain the reason PFOE described-processes are less common than PSOE [17] . In terms of adsorption progress rate of a pollutant, Langumir first order kinetic is expressed in differential form as

(7)

where F and represent adsorption progress and first order rate constant respectively.

Performing the integration operations on Equation (7), it becomes

(8)

First order kinetic rate constant, is the gradient of the plot of vs t.

Then F value is given as follows

(9)

If we recall that adsorption progress is the ratio of amount of pollutant adsorbed at time, t and amount adsorbed at equilibrium (i.e. value F at first order operation), then F is expressed as

(10)

To obtain the standard first order equation, Equation (10) is substituted into (9) to get

(11)

On the other hand, second order kinetic equation is expressed with adsorption progress as follows

(12)

where is second order rate constant.

The equation, i.e. Equation (12), can be expressed after due integration operations as follows

(13)

The standard form of Equation (13) is expressed as

(14)

Studies have also shown that pseudo-second order equation is commonly used to describe adsorption kinetics in a systems characterized with heterogeneous porous medium. In some of these studies, most researchers also used the linearized form of Equation (14) as presented in Equation (15) to authenticate its fitness to an adsorption system.

(15)

However, there were adsorption systems difficult to describe by pseudo first or second order kinetic. These systems were observed to display behavioral patterns in between the aforementioned kinetic equations (pseudo first and second [14] [15] . In that regard, a kinetic model corresponding to the combination of pseudo first and second order kinetics referred to as mixed 1,2 kinetic order equation (MOE) was introduced to fit the systems. This equation is expressed as follows;

(16)

where and represent first and second order rate coefficients while F and are the dimensionless adsorption progress and pseudo second order contribution coefficient respectively. After arranging Equation (16) with a condition of we obtained Equation (17) and its corresponding integrated form written as expressed in Equation (18a)

(17)

(18a)

Equation (18a) can be written in standard form by substituting F with Equation (10) to obtain Equation (18b)

(18b)

Being part of first order kinetic, MOE can perform the functions of largagreen equation (PFOE) whenever becomes zero or expressed as unity. In the light of that, MOE takes the form of PFOE expressed with its integrated standard form as stated in Equations (8), (9) and (11). With its peculiar integrated form, MOE can describe the kinetic behavior of wide range of adsorption systems [4] . in terms of adsorbent surface heterogeneity, PFOE, PSOE and MOE as they appear in Equations (9), (13) and (17), can describe porous adsorption systems characterized by energy and structural heterogeneity [9] but the description by MOE cannot be linked to Langmuir Kinetics unless is related to adsorption uptake and equilibrium coverage expressed as follows;

(19)

1.4. Fractal-Like MOE

Generally, fractal-like kinetic models are introduced in the adsorption study to interpret complex adsorption systems especially the energetically heterogeneous solid surfaces. This implies that an adsorption system characterized by different adsorption surface sites with consequent different affinity for adsorption has been successfully described by fractal-like kinetic models. Previous studies have presented fractal-like models based on PFOE, PSOE, MOE, IKL etc. [33] but this study will consider applicability of fractal-MOE on the adsorption system under investigation and this is expressed as

(20a)

The linear form of the equation is expressed at different values of. For the linearized version of equation is expressed as

(20b)

While at the equation becomes,

(20c)

where p is fractal coefficient.

1.5. Langmuir Equilibrium Isotherm

As it is important to get a suitable adsorbent to drive an adsorption system, so is it essential to find appropriate adsorption isotherm which defines solute interaction with the adsorbent, the surface properties and capacity of adsorbents with consequent effective adsorption mechanism. In the past, several adsorption isotherms (Langmuir, Freunlich, Brunauner-Emmett-Teller, Temkin, Toth etc.) have been adopted to describe adsorption systems. Whereas Brunauner-Emmett-Teller (BET) has been adopted to analyse gas adsorption systems, Langmuir and Freunlich models have been frequently used to describe solid/liquid interface. Monolayer and heterogeneous adsorbent respectively [18] were considered in formulating these models (Langmuir and Freunlich). Recently, combination of Langmuir and Freunlich isotherms referred to as Langmuir and Freunlich (LF) isotherm was introduced to describe adsorption Kinetics in non-ideal systems characterized with energy heterogeneity and lateral interactions (Adam et al. 2015) [19]

(21)

Applications of LF equilibrium kinetics model have proven successful in describing behavioral pattern of an adsorption system with strong heterogeneity effects [3] [20] . n value (0 to 1) in the isotherm model represents levels of heterogeneity of Langmuir adsorption system. It was observed that heterogeneity of adsorption, (level of different solute adsorptions on various adsorption sites) is inversely proportional to n values. High heterogeneity for adsorption of certain system takes place at lower n values. In terms of adsorption energy dispersion, Langmuir adsorption systems with heterogeneity parameter range of (0.34 ≤ n ≤ 81) are likely to experience moderate adsorption energy dispersion [19] . To analyze equilibrium experimental data, equation 21 is written in linear form as follows;

(22a)

where

(22b)

represents adsorbent capacity.

n values for various adsorption systems were obtained from the gradients of vs plots.

1.6. Diffusion Mechanism

Diffusion mechanism of solute into the solid phase involves several steps; movement of solute from aqueous solution to the external surface of the solid phase (film diffusion), diffusion of the solute from the surface to the interior surface of the adsorbents and the particle diffusion (transport of solute into the pores of the adsorbent). Transport to the interior surface has been reported as been the fastest step thus not considered a rate determining step. However, film and particle diffusion steps in adsorption processes are determined by two major models; Boyd and Webber kinetic models. The equation developed by Boyd and modified by Reichenberg (22) has been applied to test the prevailing steps.

(23a)

Boyd kinetic model was modified at various values of F at,

(23b)

At,

(23c)

Recall that

(23d)

where is the amount of adsorbate adsorbed with time, while is that amount adsorbed at equilibrium.

A linear plot of vs t without passing through the origin confirms film diffusion system, but particle diffusion controls the adsorption system if the line curve passes through the origin. The effective diffusion coeffi-

cient can be calculated from the slope of the curve designated as where is the effective diffusion coefficient while r is adsorbent particle radius.

To further describe the diffusion mechanism, Webber kinetic model (Equation (24)) is equally applied to determine whether film or intra-particle diffusion controls the adsorption system.

(24)

is the intra-particle coefficient. Webber kinetic model confirms an inter-particle diffusion controlled adsorption system if the straight line curve of vs passes through the origin. The equation also confirms film diffusion controlled adsorption system if the curve does not pass through the origin. Intercept of this curve expresses the value of boundary layer effect. It was observed that the intercept shows the extent surface sorption contributes to the rate determining step of the process [21] [22] . This implies that the more the curve moves away from the origin towards higher y-axis values, the higher the possibility of boundary film diffusion controlling the adsorption process. Studies have affirmed that the deviation of the curve from origin is occasioned by the variation of rate of mass transfer during the adsorption process.

In this study the possibility of applying activated carbon of oil bean seed shell (OBSS), unripe plantain peel (UPP) and castor bean seed shell (CBSS) to remove Dichlorvos and Cypermethrin from aqueous solution was explored through adsorption process. Adsorption Isotherms and kinetics of this study were carried out and their data analyzed using the models described above.

2. Materials and Methods

2.1. Adsorbent Characterization

OBSS, UPP and CBSS were collected from Nkwo market in Ogidi, Anambra state. The substances were washed with ordinary water and re-washed with distilled water to remove the dirt and other adhering substances, after which, the washed substances were sundried for three weeks, ground and sieved to appropriate particle size of 1.18 mm. The sieved samples were washed with distilled water and oven dried at temperature of 120˚C before activation with 1 M H₃PO₄ in a ratio of 1:2 to form a paste samples. Thereafter, the paste samples were oven dried at 120˚C for 24 hours before transferring to the muffle furnace where they were charred at 400˚C for 2 hours to bring the substances (OBSS, UPP and CBSS) in activated carbon form and suitable adsorbents for this study.

2.2. Adsorbate Characterization

Cypermethrin [Cyano-(3-phenoxyphenyl)methy]3-2,2-dichloroethenyl-2,2-dimethylcyclopropane-1-carboxylate] and Dichlorovos [O-O-Dimethyl-O-(2,2-Dichlorovinyl)phosphate] pesticides were used as absorbates. There chemical structures are shown as Figure 1 and Figure 2. Note that pesticides, absorbates, Cypermethrin and Dichlorovos as the case may be, will be used interchangeably in the course of this study. The two pesticides were sourced at an agro-chemical store, preparation of stock solutions and further characterizations followed standard process.

2.3. Adsorption Equilibrium Experiments

Nitrogen adsorption isotherm study and standard calculation methods at 77 K as adopted by Adam et al. 2013 [20] were carried out on the respective adsorbents to determine the total volumes, hydraulic pore size

, specific surface area and external surface area of various adsorbents. Linear BET Plots of a (cm³/g) vs and alpha plot represented as a (cm³/g) vs were made from the Nitrogen adsorption isotherm data obtained from amount of gas adsorbed with respect to applied pressure. was determined at relative pressure of plot of amount of gas adsorbed with respect to the pressure applied [a (cm³/g) vs] whereas the external surface area was determined by the alpha plot. Hydraulic pore sizes

of various adsorbents were calculated by the help of an equation described by the ratio of the total volume and specific surface area.

(25)

Equilibrium study was further carried out in aqueous solution through batch process. Two sets of experiment; each having three 500 ml conical flask containing different types of adsorbent (each adsorbent type per flask) were set-up. contents of the three conical flasks of the first set of experiment were treated with 20 mg/l of cypermethrin whereas the contents of the conical flask of the second set were treated with same concentration of Dichlorovos. The six flasks which were at pH of 6 were agitated with magnetic stirrer and allowed for adequate contact between adsorbents and the aqueous solution of the herbicides (adsorption), until adsorption equilibrium is established. After which the supernatant is decanted and analyzed for Cypermethrin and Dichlorovos in solution and on the adsorbents at equilibrium. The entire process was repeated five more times to accommodate a wide range of initial concentrations (40, 60, 90, 100, 120 and 150 mg/l) and data obtained from the equilibrium study was tested with Freundlich, Langmuir and Freundlich-Langmuir isotherm models.

2.4. Adsorption Kinetic Experiments

The aqueous solution of Cypermethrin of concentration of 100 mg/l was made to contact with adsorbents in the first three conical flask whereas aqueous solution of Dichlorovos of same concentration was introduced into the second set of three flasks also containing the adsorbents. The sets were agitated by a magnetic stirrer and at definite time intervals samples of the solution were collected for analysis of Cypermethrin and Dichlorovos. The kinetic experimental data were analyzed by conventional and Langumir kinetic models described above.

3. Results and Discussions

3.1. Properties of Adsorbates and Adsorbents

Figure 1 presents the behavior of nitrogen adsorption process on the three adsorbents (OBSS, UPP and CBSS) used in this study. Large amounts of the nitrogen gas was adsorbed on the CBSS at low temperature. On the other two adsorbents, more nitrogen gas seemed to be adsorbed on UPP than OBSS. These nitrogen gas adsorption differences are explainable by varying adsorbent pore sizes. Increase In nitrogen adsorption shown in Figure 1 was perhaps due to large number of small sized pores of CBSS adsorbent. It is quite possible that CBSS may have pore sizes close to micro-pores [23] .

Properties of the activated carbons (OBSS, UPP and CBSS) obtained by using nitrogen adsorption isotherm and methods of calculation are presented in Table 1. Results of nitrogen adsorption isotherm showed remarkable differences on the surface properties of the activated carbons. Among the adsorbents, OBSS has the highest surface property values, followed by UPP with CBSS having the least values and the trend varies in this order; OBSS > UPP > CBSS.

Results of the Properties of Dichlorovos (DI) and Cypermethrin CY are shown on Table 2. Apparent

variations were also observed on the adsorbate properties. Cypermethrin (CY) has higher values of molecular weight and volume but lower values of solubility and density than Dichlorovos (DI).

In adsorption processes, properties of adsorption components such the adsorbate in aqueous solution and the adsorbent are major key factors of adsorption. For example, large and low solubility have been observed to produce robust adsorption processes and fast kinetics, because largesurface and external areas of the adsorbents have provided ample sites for adsorption. Large hydraulic pore sizes encouraged easy pore diffusion of the adsorbates. Moreover, low soluble adsorbates have high affinity for solid surface adsorption [3] [24] .

3.2. Equilibrium Isotherms

Figure 2 represents varying levels of adsorption capacity of various adsorption systems. Cypermethrin showed more adsorption affinity to various adsorbents (CY/OBSS > CY/UPP > CY/CBSS) than Dichlorovos (DI/OBSS > DI/UPP > DI/CBSS). The apparent variations were attributed to differences in the properties of CY and DI. For example, Solubility of the adsorbates (Cypermethrin and Dichlorovos) played a key role in adsorption affinity of the adsorbates. Cypermethrin was less soluble than Dichlorovos because the intermolecular hydrogen bond formation existing between molecules of Cypermethrin resulted to weak salvation effects and high precipitation [3] [24] , in so doing creating strong adsorption affinity to the adsorbents. Surface properties of adsorbents also contributed to the prevailing adsorption trend. By virtue of its large hydraulic pore sizes, large external surface and specific area, surfaces of OBSS created adequate adsorption energy which facilitated easy and robust adsorption. Other adsorbents with lesser expanse of surface and external areas and lesser hydraulic pores had less adsorption amounts of CY and DI. To test the suitability of the isotherm models, the data obtained from adsorption equilibrium study were fitted into Freundlich, Langmuir and Langmuir-Freundlich (LF) isotherms. it was observed that the data have weak relationships with Freundlich and Langmuir (graphs not shown for brevity ) however, LF produced stronger relationship as indicated by high correlation coefficient values of Figure 3, hence repre- senting the data batter than the other two isotherms.

This scenario, confirmed the heterogeneity status of the adsorption systems [23] [25] which was further testified by the heterogeneity parameter, n of between 0.34 and 0.62 as shown on Table 3. Comparing the L-F parameters obtained from the plotted equilibrium data shown in Figure 3, CY/OBSS and DI/OBSS adsorption systems showed strong heterogeneity given low n values associated with them. From the table, adsorption capacity and equilibrium adsorption constants K corresponded with the heterogeneity status of CY/OBSS and DI/OBSS adsorption systems. This implies that with strong heterogeneity status of CY/OBSS and DI/OBSS there were corresponding high adsorption capacities and adsorption constants K, suggesting high affinity for adsorption [3] [20] .

The apparent high potential for adsorption exhibited by OBSS could also be attributable to large properties whereas the small surface areas and hydraulic pores sizes of UPP and CBSS might restrict access of adsorption of DI and CY to the adsorbents [3] [24] . The high solubility status of

Dichlorovos which made it scarcely available (precipitated form) in solution for adsorption could explain the apparent low DI affinity for adsorption [3] . Complication in surface reactions, where foreign materials other than the adsorbates under study, adsorbed on the solid surface causing reduction in the effective surface area of the adsorbents with consequent reduction in the rate of adsorption, could also be a factor in the observed low adsorption affinity [26] [27] ). This process could inhibit DI and CY adsorption access to the affected adsorbents.

3.3. Adsorption Kinetic Study

Data obtained from the kinetic experiment were fitted into the kinetic models (PSOE, MOE, IKL and F-MOE) with the view of getting the model(s) which best described the study. The results are shown on Figure 4(a) and Figure 4(b) as amounts of adsorbate uptake (1-F) data with respect to time scale data for the adsorbates (CY and DI) and adsorbents (OBSS, UPP and CBSS). The time scale was calculated based on the following equations and conditions;

(26a)

(26b)

The figures show different adsorption kinetic processes for different systems. Figure 5(a) shows various adsorption kinetic processes in Cypermethrin associated systems (CY/OBSS, CY/UPP, and CY/CBSS) whereas Figure 5(b) shows that of Dichlorovos related systems (DI/OBSS, DI/UPP and DI/CBSS). The adsorption kinetic models described adsorption kinetics rates of various systems in different manner. In Cypermethrin associated systems, IKL, MOE and F-MOE models described CY uptake reduction by OBSS as being the slowest, in UPP the reduction uptake was moderately slow whereas the reduction rate was fast in CBSS. The slow uptake reduction implies that CY adsorption stretched to a long contact period with high amount of CY adsorbed on

OBSS system. CY uptake reductions were fast in UPP and CBSS with less amount adsorbed CY as described by the kinetic models. This proved that little contact time was made between CY and UPP and CBSS, resulting to low CY adsorption. IKL and F-MOE models described the behavior of CY uptake reduction rate on CBSS as slow, with little amount of CY adsorbed. The high initial CY uptake and various reduction rates shown by the kinetic curves could be attributed to differences in surface properties and hydraulic pores of the adsorbents. CY/OBSS and CY/OBSS systems virtually maintained high initial uptake and gradual reduction in uptake values, suggesting that CY has strong adsorption affinity OBSS adsorbent due to large properties and strong heterogeneity effects of the adsorbent. The rate of CY uptake reduction is fast in UPP and CBSS absorbents where CY showed little affinity due to small surface specific and external areas and hydraulic pore sizes.

This was not exactly the case in Dichlorovos associated systems as shown on Figure 5(b). Although PSOE, IKL and MOE described DI uptake reduction in OBSS system as being slow with high DI initial uptake but DI rate reduction uptake onto UPP as described by IKL, MOE and PSOE, became slower with time. Also, F-MOE described DI rate reduction uptake as fast. The deviation from earlier observation on CY associated systems could be attributed to surface inhibition during DI contacts with the adsorbents. The fast rate observed in MOE described DI/OBSS system could be a typical example. It means that less amount of DI was adsorbed on OBSS system despite its high surface property values.

The models were further applied to test their Suitability on the kinetic data of various systems. There was better agreement between the experimental data of CY/OBSS system and the fitted curves of F-MOE than other models. The correlation was testified by high value hence making F-MOE a confirming model for the system. The models were also tested on the kinetic data of CY/UPP and CY/CBSS. IKL and MOE models showed better agreement than other models with the experimental data of the respective systems. High values of 0.90 and 0.80 respectively confirmed the relationships. With the good correlations, IKL and MOE models were expressed as the confirming models. In testing the kinetic data obtained from DI/OBSS, DI/UPP and DI/CBSS, good fits were obtained for IKL, MOE and PSOE on the data systems respectively. Table 3 also shows the overview of the correlation coefficient of various adsorption systems.

4. Diffusion Mechanism

Diffusion models were applied on the adsorption progress data to determine the prevailing rate determining steps. Results of the two major diffusion models shown on Figure 6(a) and Figure 6(b) confirmed the film diffusion of Cy and DI on the adsorbents as the prevailing rate determining step. This is because none of the curves passed through the origin. The situation is apparently due to one or more of these factors; (a) poor phase mixing, (b) dilute concentration of adsorbate, (c) small particle size, and (d) high affinity of the adsorbate for the adsorbent [28] - [30] . Previous researchers have affirmed that the more the curve deviates from the origin towards higher y-axis values, the higher the possibility of boundary film diffusion controlling the adsorption process.

The deviations from the origin were occasioned by variations of rate of mass transfer of the adsorbates during adsorption process [31] [32] . In that light, and also following Webbers kinetic model, Cypermethrin experienced a measure of film diffusion on OBSS more than on other adsorbents perhaps due to its high affinity for the adsorbent [33] - [36] .

Moreover, levels of film diffusion of the adsorbates (CY and DI) on the other adsorbents were virtually same. From Boyd kinetic model curves, Dichlorovos has higher film diffusion on OBSS system than on the other systems. Film diffusion Reduction trend on the systems as described by Boyd is as follows; DI/OBSS > DI/UPP > CY/CBSS > DI/CBSS > CY/OBSS > CY/UPP.

5. Conclusions

Adsorption of Cypermethrin and Dichlorovos onto activated OBSS, UPP and CBSS has been studied. There were different property values of both the adsorbents and adsorbates. Cyoermethrin was less dense and less soluble than Dichlorovos and variations of values in the activated adsorbents were also observed. Cypermethrin has more adsorption affinity towards the adsorbents than Dichlorovos. Its (cypermethrin) low solubility was due to the perceived affinity. Furthermore, OBSS has good adsorption capacity and the capacity is in consonant with property values of the adsorbents, hence the following order of adsorption capacity OBSS > UPP > CBSS.

L-F adsorption isotherm model fitted the adsorption equilibrium data better than other isotherm models. Uptake reduction of DI and CY was assessed using the kinetic models (MOE, F-MOE, IKL, POSE). IKL, MOE and F-MOE models described CY uptake reduction by OBSS with high amount of adsorbed CY, as being the slowest among UPP and CBSS adsorbents. The reduction rate is fast, with little amount of adsorbed CY on UPP and fastest on CBSS. On the other hand, IKL, MOE and PSOE described DI reduction rate by UPP, as being the slowest with reasonable high initial amount of adsorbed DI. F-MOE, IKL, PSOE and MOE kinetic models were used to test the agreement between the kinetic data of respective systems and the models. F-MOE, IKL and MOE were found the best fit for CY/OBSS, CY/UPP and CY/CBSS systems respectively;hence the conforming models, whereas in DI/OBSS, DI/UPP and DI/CBSS adsorption systems, had good fits with IKL, MOE and PSOE respectively. The two applied diffusion models (Boyd and Webbers) confirmed film diffusion pattern as prevailing transportation pathway of CY and DI onto the adsorbents.

Cite this paper

Atulegwu Patrick Uzoije,Clifford O. Kamalu,Uzuakpundu Basil, (2015) Adsorption Kinetics and Mechanisms of Cypermethrin and Dichlorovos on Heterogeneous Activated Carbon Porous Media. Open Access Library Journal,02,1-15. doi: 10.4236/oalib.1101988

References