Received 24 October 2015; accepted 8 November 2015; published 13 November 2015

ABSTRACT

In this article we are going to introduce certain applications of the theory of neural network to medicine. In particular suppose for a given disease D, belonging to the category of immune deficiency diseases or cancers, there are numbers of drugs each with partial remedial effect on D. We are going to formulate a cocktail consisting of mixture of the above drugs with optimal remedial effect on D.

Keywords:

Disease, Cocktail, Optimization, Neural Network, Back Propagation, Trails, Data

Subject Areas: Drugs & Devices

1. Introduction

Many problems in the industry involved optimization of certain complicated function of several variables. Furthermore there is usually a set of constrains to be satisfied. The complexity of the function and the given constrains make it almost impossible to use deterministic methods to solve the given optimization problem. Most often we have to approximate the solutions. The approximating methods are usually very diverse and particular for each case. Recent advances in theory of neural network are providing us with a completely new approach. This approach is more comprehensive and can be applied to a wide range of problems at the same time. In the preliminary section we are going to introduce the neural network methods that are based on the works of D. Hopfield, Cohen and Grossberg. One can see these results at Section-4 [1] and Section-14 [2] . We are going to use the generalized version of the above methods to find the optimum points for some given problems. The results in this article are based on our common work with Greg Millbank of praxis group. Many of our products used neural network of some sorts. Our experiences show that by choosing appropriate initial data and weights we are able to approximate the stability points very fast and efficiently. In [3] , we introduce the extension of Cohen and Grossberg theorem to larger class of dynamic systems. The appearance of new generation of super computers will give neural network a much more vital role in the industry, intelligent machine and robotics.

2. On the Structure and Application of Neural Networks

Neural networks are based on associative memory. We give a content to neural network and we get an address or identification back. Most of the classic neural networks have input nodes and output nodes. In other words every neural networks is associated with two integers m and n. Where the inputs are vectors in 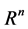and outputs are vectors in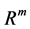. Neural networks can also consist of deterministic process like linear programming. They can consist of complicated combination of other neural networks. There are two kind of neural networks. Neural networks with learning abilities and neural networks without learning abilities. The simplest neural networks with learning abilities are perceptrons. A given perceptron with input vectors in 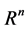and output vectors in,

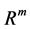is associated with threshold vector 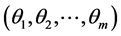and matrix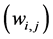. The matrix W is called matrix of synaptical values. It plays an important role as we will see. The relation between output vector and input vector 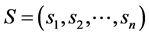is given by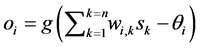, with g a logistic function usually

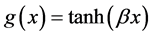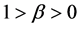given as with This neural network is trained using enough number of corresponding patterns until synaptical values stabilized. Then the perceptron is able to identify the unknown patterns in term of the patterns that have been used to train the neural network. For more details about this subject see for example (Section-5) [1] . The neural network called back propagation is an extended version of simple perceptron. It has similar structure as simple perceptron. But it has one or more layers of neurons called hidden layers. It has very powerful ability to recognize unknown patterns and has more learning capacities. The only problem with this neural network is that the synaptical values do not always converge. There are more advanced versions of back propagation neural network called recurrent neural network and temporal neural network. They have more diverse architect and can perform time series, games, forecasting and travelling salesman problem. For more information on this topic see (Section-6) [1] . Neural networks without learning mechanism are often used for optimizations. The results of D. Hopfield, Cohen and Grossberg, see (Section-14) [2] and (Section-4) [1] , on special category of dynamical systems provide us with neural networks that can solve optimization problems. The input and output to these neural networks are vectors in 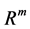for some integer m. The input vector will be chosen randomly. The action of neural network on some vector consist of inductive applications of some function 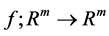which provide us with infinite sequence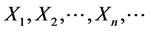, where . And output (if exist) will be the limit of the above sequence of vectors. These neural networks are resulted from digitizing the corresponding differential equation and as it is has been proven that the limiting point of the above sequence of vector coincide with the limiting point of the trajectory passing by. Recent advances in theory of neural networks provide us with robots and comprehensive approach that can be applied to wide range of problems including pattern recognition and simulations that can be applied to varieties of cancers and immune deficiency diseases. At this end we can indicate some of the main differences between neural network and conventional algorithm. The back propagation neural networks, given the input will provide us the output in no time. But the conventional algorithm has to do the same job over and over again. On the other hand in reality the algorithms driving the neural networks are quite massy and are never bug free. This means that the system can crash once given a new data. Hence the conventional methods will usually produce more precise outputs because they repeat the same process on the new data. Another defect of the neural networks is the fact that they are based on gradient descend method, but this method is slow at the time and often converge to the wrong vector. Recently other method called Kalman filter (see Section-15.9 [2] ) which is more reliable and faster been suggested to replace the gradient descend method. At this end we have to mention that many exiting results on applications of neural networks to optimization can be found in [4] .

3. On Providing a Cocktail Consisting of Certain Drugs Having Optimum Effect

Suppose there is a certain disease D. Next assume that there are number of drugs available to treat D. Let the vector represent the health state of the body. Assume the vector represent the vital limitation of the body. Next let, respectively, represent the initial health state of the body, respectively (the initial vital state of the body). Suppose that the daily use of the amount milligram of the product will finally drive the body to the health state which is represented by the vector,

respectively (will drive the vital state of the body to the state which is represented by the vector).

We are searching for the optimal solution where the cocktail consisting of certain daily amount from each product, will provide us with the final health state and final vital state such that they satisfy, the following properties,

to minimize,

and to maximize

keeping the constrain.

Beside that we usually have to consider certain limitation of daily use of each one of the products which are expressed in the following inequalities,

.

The above conditions are equivalent in optimization the function F, given in the following

Together with the set of constrains

and

where is an arbitrary positive number chosen in an appropriate way, usually at the same magnitude as to the set.

Finally the above system of optimization corresponds to the following energy function,

where, are fixed positive numbers that are chosen in an appropriate way.

Also we can choose simpler approach by formulating the energy function E in the following

where we keep the set of constrains, and consider as an independent variable to be added to the set of variables, and set it to be equal to.

The problem with this approach is that now the boundary points can be candidate for optimum point too.

Provided we have the values,

, for each vector

then using the arguments in [3] , we are able to calculates immediately the vector that will give us the optimum, where represent the set of all positive real. For example If the values of, can be assumed to be equal a linear sum of, , then we are done, otherwise if the assumption of linearity fails we have to use a back propagation neural network, as we describe at the Section-1. In this case first we have to train the neural network using sufficiently many experiences on randomly chosen patients with randomly chosen parameters

This process depending on the number of available patients and duration of the trails might takes up to two years. At this point we have to mention that though it seems very complicated but in the future the simulation on neural network might replace the human trails which will contribute immensely to the field of medical research.

Next we feed the vectors, corresponding to the randomly chosen patient of the above to back propagation neural network, for training. Once the training is complete, for a given vector

the neural network, will provide us with the vectors .

Finally for a given small, suppose the set of vectors are chosen such that they will cover up to the above the interval

.

Next let be the vector to optimize the energy function, hence to give us the optimum cocktail for a patient with a initial condition.

Now when we feed the new patient with the optimum cocktail, to the end of the trail we measure the actual values of and comparing them with the neural network output , the differences will be used to train further the back propagation neural network and to get new synaptical values. Hence after many trails the neural network will be able to find the exact optimum values for the cocktail that is appropriate for the patient with initial condition.

4. Conclusion

There is a set of diseases which cannot be cured using the existing set of drugs. But some of the above drugs can improve the state of health of an infected person. We suggest that it is possible to make a cocktail consisting of the above drugs which will provide us with the most effective treatment of the above person. We suggest that this method can be set on trails and be examined.

Cite this paper

Bahman Mashood,Greg Milbank, (2015) Application of Neural Network to Medicine. Open Access Library Journal,02,1-4. doi: 10.4236/oalib.1102067

References