Received 24 March 2016; accepted 12 July 2016; published 15 July 2016

ABSTRACT

This paper mainly tends to utilize Razumikhin-type theorems to investigate p-th moment stability for a class of stochastic switching nonlinear systems with delay. Based on the Lyapunov-Razumik- hin methods, some sufficient conditions are derived to check the stability of stochastic switching nonlinear systems with delay. One numerical example is provided to demonstrate the effectiveness of the results.

Keywords:

Stochastic Switching Delay System, p-th Moment Stability, Lyapunov-Razumikhin Approach

1. Introduction

Stochastic switching system is an indispensable class of hybrid dynamical systems, which is composed of a family of stochastic subsystems and a rule that orchestrates the switching among them. Yet, there inevitably exists delay phenomenon in the practical systems like physics, biology and economic [1] [2]. So it is important for us to study stochastic switching systems with delay. Over the previous few decades, stochastic switching delay systems have received much attention due to their potential applications in many fields, such as the control of mechanical systems, automotive industry, chemical and electrical engineering [3] [4].

It is well-known that stability is the major issue of control theory. Lyapunov-Razumikhin technique has been a powerful and effective method for investigating stability. Razumikhin developed this technique to study the stability of deterministic systems with delay in [5] [6], then, Mao extended this technique to stochastic functional differential equations [7] and neutral stochastic functional differential equations [8] to investigate p-th moment exponential stability of this systems. Later, this technique was appropriately developed and extended to some other stochastic systems, such as hybrid stochastic delay interval systems [9] and impulsive stochastic delay differential systems [10]. Recently, some researchers have introduced 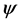-type function and extended the stability results to 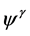stability, including the exponentialstability as a special case in [11] [12]. In [13], the researchers utilize multiple Lyapunov functions investigate the stability of stochastic switching nonlinear systems.

To the best of our knowledge, there are no results based on the Razumikhin approach referring to the stability of stochastic switching nonlinear systems with delay. The main aim of this paper is to attempt to investigate p-th moment 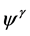stability of stochastic switching delay nonlinear systems. By the aid of Lyapunov-Ra- zumikhin approach, we obtain the p-th moment 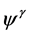stability of stochastic switching systems with delay in Section 3. An example is presented to illustrate the main results in Section 4. Finally, the conclusions are given in Section 5.

2. Preliminaries

Consider a family of stochastic switching delay nonlinear systems described by

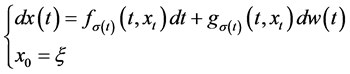(1)

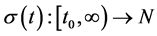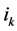where is the switching signal, let be a switching sequence and the - th subsystem is active at time interval, where 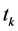is the switching instant, ,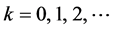. System (1) is consisted with many stochastic subsystems 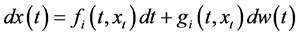which are driven

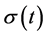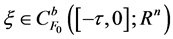by switching signal., and is finite,

is an m-dimensional independent standard Wiener process, and the underlying complete probability space is taken to be the quartet with a filtration satisfied the usual conditions (i.e. it is increasing and right continuous while contains all P-null sets), functions, are both measurable and let, ,.

Definition 1. is said to be -type function, if it satisfies the following conditions:

1) It is continuous, monotone decreasing and differentiable;

2) and, as;

3);

4) for any,.

Definition 2. For, stochastic switching delay nonlinear systems (1) is said to be p-th moment stable, if there exist positive constants and function, such that

(2)

when, we say that it is stable in mean square, when, we say that it is p-th moment exponential stable, when, we say that it is p-th moment polynomial stable.

Before giving the main results, let us introduce formula. For system (1), give any function and define an operator described by

where

3. Main Results

In this section, we shall establish Razumikhin-type theorems on the p-th moment stable for stochastic delay nonlinear systems by using Razumikhin technique and Lyapunov functions. Before giving the efficient theorem, let us give some assumptions to the switching signal.

Assumption 1. Switching signal is right continuous and state-dependent.

Assumption 2. At each switching instant, the state trajectory is not jumped.

Then, let us turn our attention to system (1) and give a sufficient result.

Theorem 1. For stochastic switching delay nonlinear systems (1), if there exist a group of Lyapunov functions and positive constants, such that

(3)

(4)

for all, and those satisfying

(5)

where.

and at each switching instant,

(6)

where.

Then, for any initial, there exists a solution on to stochastic

switching delay nonlinear system (1). Moreover, the system (1) is p-th moment stable and

. (7)

Proof. Fix the initial data arbitrarily and write simply. When is

replaced by, if we can prove (7) for all, then the desired result is obtained.

Given switching signal and instant for arbitrary, assume that is the last switching instant before, i.e. there is no switching occur on the interval.

Let be arbitrary, if we can prove

we will complete this proof. By condition (6), this result follows from

Let, we have

(8)

By the continuity of, it is obvious that

.

We claim that (8) holds for all.

In order to do so, we first prove that

That is

(9)

This can be verified by a contradiction, suppose that inequality (9) is not right, then by the continuity of

, there exists a smallest such that for and as well

as for all sufficiently small, then for, if and

, by condition (3), we have

(10)

if, then since, we, therefore, obtain

(11)

Therefore, for, we have

By condition (4), we can obtain

By the continuity of, for all sufficiently small, when, we have

By the formula and continuity of, for all sufficiently small, we can obtain

By condition (4)

which is a contradiction. Hence, inequality (9) holds for all, and inequality (8) is right for.

Now, let. We assume that inequality (8) holds for, i.e.

(12)

That is

(13)

We will prove that

(14)

Suppose that inequality (14) is not right,

By condition (6) and inequality (12), we have

(15)

That is

Then by the continuity of, there exists a smallest such that for,

and as well as for all suffi-

ciently small, then for, if, then from (15), we have

(16)

if, then since, we, therefore, obtain

(17)

Therefore, for, we have

By condition (4), we can obtain

By the continuity of, for all sufficiently small, when, we have

By the formula and continuity of, for all sufficiently small, we can obtain

By condition (4)

which is a contradiction. Hence, inequality (14) holds for all.

Therefore, by mathematical induction we obtain (8) holds for all.

Then, , we have

.

That is

.

Thus, the system (1) is p-th moment stable.

4. Example

In this section, a numerical example is given to illustrate the effectiveness of the main results established in Section 3 as follows.

Consider a family of stochastic switching delay nonlinear systems

where is switching signal. Let be a switching sequence and the th subsystem is active at time interval, where is switching instant, and.

We choose, , , , , then, , , , ,.

When, we choose and for the first subsystem; when, we choose and for the second subsystem.

For the first subsystem, we choose, then. If, we have

If, then.

For the second subsystem, we choose, then. If, we have

If, then.

By Theorem 1, we can choose, then, , which means that the conditions of Theorem 1 are satisfied. So the stochastic switching delay nonlinear systems are p-th moment stability. The switching signal and the state trajectory are presented in Figure 1 and Figure 2, respectively.

Remark. In the example, a stochastic switching delay nonlinear system is constructed to show the efficiency of the results. Figure 1 describes switching signal changes over the time. Figure 2 depicts state trajectory changes over the time, the blue line describes the systems with delay and the red describes the systems without delay.

5. Conclusion

In this paper, p-th moment stability has been investigated for stochastic switching nonlinear systems with delay. Some sufficient conditions have been derived to check the stability criteria by using the Lyapunov-Ra-

zumikhin methods. A numerical example is provided to verify the effectiveness of the main results. Our future research will focus on stability of neutral stochastic switched nonlinear systems and stability of impulsive stochastic switched delay nonlinear systems.

Acknowledgements

The work was supported by the National Natural Science Foundation of China under Grants 11261033 and the Postgraduate Scientific Research Innovation Foundation of Inner Mongolia under Grant 1402020201336.

Cite this paper

Haibo Gu,Caixia Gao, (2016) Razumikhin-Type Theorems on p-th Moment Stability for Stochastic Switching Nonlinear Systems with Delay. Journal of Applied Mathematics and Physics,04,1237-1244. doi: 10.4236/jamp.2016.47129

References