Received 28 December 2015; accepted 12 July 2016; published 15 July 2016

ABSTRACT

Existence of traveling wave solutions for some lattice differential equations is investigated. We prove that there exists 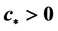such that for each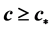, the systems under consideration admit monotonic nondecreasing traveling waves.

Keywords:

Traveling Wave, Lattice Dynamical Systems, Schauder’s Fixed Point Theorem

1. Introduction

Consider the following lattice differential equation

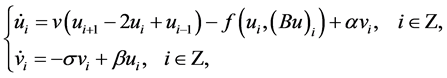(1.1)

where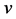, 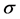are positive constants, 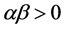, 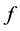is a 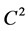-function, and.

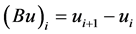Lattice dynamical systems occur in a wide variety of applications, and a lot of studies have been done, e.g., see [1]-[4]. A pair of solutions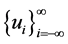, 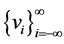of (1.1) is called a traveling wave solution with wave

speed 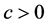if there exist functions 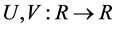such that, with and. Let, note that (1.1) has a pair of traveling wave solutions if and only if, satisfy the functional differential equation

(1.2)

Without loss of generality, we can impose (1.1) with asymptotic boundary conditions

, , ,. (1.3)

By the property of equation, we can assume that. In the following, we give some assumptions on nonlinear function:

, ,.

There exists a positive-value continuous function such that

,.

, ,

for any, ,

where, is given in Lemma 2.1.

for any.

Select positive constants such that, , and define operators by

. (1.4)

Then, (1.2) can be rewritten as

,. (1.5)

Define the operators by

.

Note that satisfy and a fixed point of is a solution of (1.2). Denote the Euclidean norm in. Define

,

where. Note that is a Banach space.

Definition 1.1. If the continuous functions are differentiable almost everywhere and satisfy

(1.6)

Then, is called an upper solution of (1.2).

Similarity, we can define a lower solution of (1.2). The main result of this paper is

Theorem 1.1. Assume that hold. Then there exists such that for every, (1.2) admits a traveling wave solution connecting and. Moreover, each component of traveling wave solution is monotonically nondecreasing in, and for each, , also

satisfy, , where is the smallest solution of the eq-

uation

.

2. Upper-Lower Solutions of (1.2)

Set.

Lemma 2.1. Assume that holds. Then there exists a unique such that if, then there exist two positive numbers and with such that , in, and in; if, then for all; if, then, and.

Proof. Using assumption, we can get the result directly.

Lemma 2.2. Assume that, and hold. Let, , and be defined as in

Lemma 2.1, and be any number. Then for every and, there exists

such that for any,

,

and

are a pair of upper solutions and a pair of lower solutions of (1.2), respectively.

Proof. Let

(2.1)

. (2.2)

Since, there exists such that,. If, then,

. By, we get that

,.

If, then. By, , and using

Lemma 2.1, we get that

(2.3)

Lemma 2.1 and yields

. (2.4)

Thus,

Therefore, is an upper solution of (1.2). Similarly, we can prove that is a lower solution.

3. Existence of Traveling Wave

Let,. We have the fol-

lowing result.

Lemma 3.1 Assume that and hold. Then

and for if

satisfy, for;

are nondecreasing in if is nondecreasing in.

Proof. If such that and for , then by we have

(3.1)

where. Note that

(3.2)

Thus, from (3.1)-(3.2), we have

which implies that. A similar argument can be done for. Thus, we can get the desired results.

Lemma 3.2. Assume that and hold. Then is continuous

with respect to the norm with.

Proof. We first prove that are continuous. Denote

. For any, choose, where

. If and satisfy

, then by (3.1),

(3.3)

Similarly, is continuous.

By definition of, we have

(3.4)

If, it follows that

. (3.5)

If, it follows that

(3.6)

Combining (3.5) and (3.6), we get that is continuous with respect to the norm. A Similar argument can be done for.

Define

It is easy to verify that is nonempty, convex and compact in. As the proof of Claim 2 in the proof of Theorem A in [5], we have

Lemma 3.3. Assume that hold. Then.

Proof of Theorem 1.1. By the definition of, Lemma 3.2-3.3 and Schauder’s fixed point theorem, we get that there exists a fixed point. Note that is nondecreasing in, as-

sumption and Lemma 2.2 imply that . There-

fore, is a traveling wave solution of (1.1).

Acknowledgements

This work was supported by the NNSF of China Grant 11571092.

Cite this paper

Xiaojun Li,Yong Jiang,Ziming Du, (2016) Existence of Traveling Waves in Lattice Dynamical Systems. Journal of Applied Mathematics and Physics,04,1231-1236. doi: 10.4236/jamp.2016.47128

References