Received 20 October 2015; accepted 4 November 2015; published 11 November 2015

ABSTRACT

A theory of relativistic traveling wave tube (RTWT) with magnetized cold plasma-filled corrugated waveguide with solid electron beam is given. The entire system influenced a strong longitudinal magnetic field that magnetized plasma and electron beam. The characteristic of the dispersion relation is obtained by numerical solutions. The effect of electron beam density, corrugated period, waveguide radius on the dispersion relation and growth rate is analyzed. Some useful results are given.

Keywords:

RTWT, Solid Electron Beam, Cold Plasma, Dispersion Relation, Growth Rate

Subject Areas: Applied Physics, Theoretical Physics

1. Introduction

Relativistic travelling wave tube (RTWT) is an important high-power microwave (HPM) apparatus which has been developed in the past 20 years [1] - [3] . Pierce and co-workers [4] - [6] employed the coupled-wave analysis in their pioneering work. The analysis of TWT is improved by using linear theories based on the Maxwell’s equations in a sheath helix [7] [8] . The coupled-wave Pierce theory recovers the near-resonant limit. Both coupled- wave and field theories of TWT have discussed in [9] . Freund and coworkers developed the field theories of beam-loaded helix TWTs for tape helix model. Freund and coworkers [8] have described the numerical comparison between the complete dispersion equation and the Pierce model in helix TWT and shown that the coupled- wave theory breaks down for sufficiently high currents. The complete field theory is more exact than the coupled-wave theory. In TWT, sinusoidal corrugated slow wave structure (SWS) is used to reduce the phase velocity of the electromagnetic wave to synchronize it with the electron beam velocity, so that a strong interaction between the two can take place [10] [11] . TWT is extensively applied in satellite and airborne communications, radar, particle accelerators, cyclotron resonance and electronic warfare system. The plasma injection to TWT has been studied recently which can increase the growth rate and improve the quality of transmission of electron beam. We investigate the effect of cold plasma and electron beam on the growth rate [12] - [17] . It is shown that the plasma has different behaviors in different density limits. On the other hand, it is shown that in the strong magnetic field limit, the maximum growth rate and frequency of all modes are constant at different values of cyclotron frequency and beam energy.

An analytical and numerical study is made on the dispersion properties of a cylindrical waveguide filled with plasma. An electron beam and static external magnetic field are considered as the mechanisms for controlling the field attenuation and possible stability of the waveguide [23] - [27] .

In this paper, a RTWT with magnetized cold plasma-filled corrugated waveguide with solid electron beam is studied. The dispersion relation of corrugated waveguide is derived from a solution of the field equations. By numerical computation, the dispersion characteristics of the RTWT are analyzed in detail in different cases of various geometric parameters of slow wave structure.

In Section 2, the physical model of the RTWT filled with cold is established in an infinite longitudinal magnetic field. In Section 3, the dispersion relation of the RTWT is derived. In Section 4, the dispersion characteristics of the RTWT are analyzed by numerical computation.

2. Physical Model

The analysis presented in this paper is based on the SWS shown in Figure 1. The SWS reduces speed of the wave is a sinusoidal cylindrical waveguide that consists of an axially symmetric. The speed wave is reduced after collision with wave guide reaching the speed of the electron beam (synchronism), so the wave is amplified.

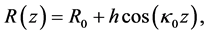(1)

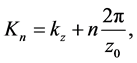(2)

Cylindrical waveguide whose wall radius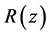, varies sinusoidal according to the relation (1), h is the corrugation amplitude, 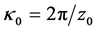is the corrugation wave number, and 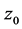is the length of the corrugation period, 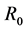is the waveguide radius and is the axial number wave.

A finite solid relativistic electron beam with density 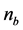and radius 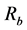goes through the cylindrical waveguide, which is loaded completely with a cold, uniform and collisionless plasma of density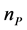. The entire system is immersed in a strong, longitudinal magnetic field, which magnetizes both the beam and the plasma. Because dielectric constant is an anisotropic so it will be a tensor. In the beam-plasma case in a linearized scheme, the dielectric tensor, in cylindrical coordinates, may be given by:

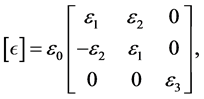(3)

We assume that 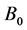is very strong that 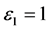and 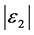is negligibly small.

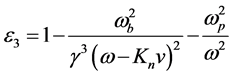(4)

Here, is the plasma frequency, is the beam frequency, ω is the angular frequency of the electromagnetic wave, is the electron beam energy, v is the velocity of the beam, and K is the Boltzmann constant.

3. Dispersion Equation

In the above physical model, its Maxwell equations can be written as:

(5)

(6)

(7)

(8)

Suppose that every variable can be regarded as:

(9)

From Equations (5) and (6), we can obtain:

(10)

(11)

Now Substituting Equation (4) into Equation (11), we have:

(12)

From Equation (10), we have:

(13)

Substituting Equation (4) into Equation (13), we obtain:

(14)

From Equations (11) and (14), the wave equation is obtained in the area of plasma-beam as follows:

(15)

(16)

(17)

(18)

We investigate ground state (n = 0) to solve the equation. Substituting Equation (17) into Equation (15), we have:

(19)

(20)

(21)

The field components must satisfy the following continuity equations (first boundary condition):

As a result, the field components are obtained as follows:

where

.

At the perfectly conducting corrugated waveguide surface (second boundary condition), the tangential electric field must be zero,

(22)

Substituting Equations (17), (18) and (19) into Equation (22), we investigate second boundary condition in ground state (n = 0) to achieve the dispersion equation.

(23)

Using the factorization of Equation (23) and substituting and, we obtain:

(24)

(25)

A is a vector with element and D is a matrix with element. With the help of derivative of Bessel functions and substituting Equation (1), the dispersion relation can be obtained and written as [18] - [22] .

(26)

4. Numerical Result and Discussion

The analysis of the dispersion relation is obtained by Equation (26). First, we consider the dispersion analysis in the absence of the electron beam.

Figure 2 shows the variation of normalized frequency Re versus wave number for several values of the corrugation periods. As seen in Figure 3, the effect of increases the frequency.

The effect of waveguide radius on the frequency of wave as a function of is shown in Figure 4. As illustrated in this figure, the frequency decreases by increasing the waveguide radius. The phase velocity of the system decreases by increasing the radius. It maybe cause to the wave exit from the resonant condition.

Now, we consider the analysis of the growth rate in the presence of the electron beam.

It is clear that from Figure 5, the growth rate increases by increasing the corrugation period. This increasing in the corrugation period helps wave to include in the resonant condition and finally increases the growth rate.

As seen in Figure 6, the growth rate decreases by increasing the. The waveguide radius has the most important role in the determination of wave phase velocity. According to Figure 4, it seems that the phase velocity decreases by increasing the radius and as seem in Figure 6 the growth rate decreases by increasing the radius. By decreasing the phase velocity the wave exits from resonant condition.

The effect of the plasma density on the growth rate as a function of the wave number is shown in Figure 7. It is clear that in this frequency range the effect of plasma density decreases the growth rate of the system.

It is clear that from Figure 8 because of bunching effect, the increasing e-beam density increases the growth. As seen from Figure 9, because of the synchronism condition, the effect of decreases the growth rate.

5. Conclusions

In this paper, useful results are obtained as follows.

1) The growth rate decreases by increasing the waveguide radius, plasma density and e-beam energy in the presence of the electron beam.

2) In the absence of the electron beam, the frequency increases by increasing the length of the corrugation period and plasma density.

3) The frequency decreases by increasing the waveguide radius in the absence of the electron beam.

4) In the presence of the electron beam, the growth rate increases by increasing the corrugation period and e- beam density.

Cite this paper

Maryam Garjasi,Shahrooz Saviz, (2015) Dispersion and Growth-Rate Characteristics of a Sinusoidally Corrugated Slow-Wave Structure in Presence of Cylindrical Electron Beam. Open Access Library Journal,02,1-10. doi: 10.4236/oalib.1102008

References