Received 19 October 2015; accepted 5 November 2015; published 11 November 2015

ABSTRACT

In this paper, we propose a rumor transmission model with incubation period considering the fact that incubators may move to stifler class and susceptibles may move to spreader class. The model is formulated with constant recruitment and varying total population. The full system of the model is studied qualitatively producing rumor-free and rumor-existence equilibriums. The existence conditions of the equilibriums are investigated. Moreover, the local and global stability analysis of both equilibriums is examined. Furthermore, numerical simulations are used to support the qualitative analysis. Finally, the impact of different management strategies on the dissipation of rumors is analyzed numerically by varying key parameters in the model.

Keywords:

Rumor Transmission Model, Local Stability Analysis, Global Stability Analysis

Subject Areas: Dynamical System, Mathematical Analysis, Ordinary Differential Equation

1. Introduction

Rumors disseminate easily these days with expanding social networks. Although rumors are neither true nor false, this does not stop some individuals from spreading it any way before searching for some kind of con- firmation. Transmission of rumors has a major impact on human lives. It may have negative sides such as causing panic and chaos in emergency events or destroying credibility of someone or something. On the other hand, it may create awareness and draw public attention to take action. As a result, great importance lies in studying the dynamics of rumor propagation.

Researchers have applied epidemiological models to study the dynamics of social systems. Daley and kendall are among the earliest researchers to propose a rumor spread model that has some properties in common with epidemic model [1] . Also Cane [2] showed the similarity among the deterministic forms of models for the spread of an epidemic and of a rumor. This is based on the fact that both biological diseases and social behavior are a result from interactions between individuals. The model in [1] [2] divided the population into three disjoint classes of individuals: susceptible, describing people who had not yet been exposed to a particular rumor; infective, referring to people who spread the rumor through social interactions; and recovered, meaning people who had experienced the rumor, but had no interest in spreading it or had lost interest at some point.

At the beginning of this century, several mathematical models are proposed considering different dynamics of rumor and idea transmission. Thompson et al. [3] explored a model for the dynamics of rumor spreading in chat rooms. Bettencourt et al. [4] applied models similar to epidemiology to study the spread of ideas. Kawachi [5] and Kawachi et al. [6] proposed deterministic models for rumor transmission and explored the effects of various contact interactions among three classes: susceptible (ignorant about the rumor), spreader (spread the rumor) and stifler (don’t spread the rumor). Later, Al-Amoudi et al. [7] [8] adopted the models in [5] to study the dynamics of constant and variable meme propagation with a comprehensive qualitative analyses. Also, they proposed a model to examine the impact of stiflers on the transmissions of memes in [9] . Wang and Wood [10] adopted an epidemiological approach to model viral meme propagation. Piqueira [11] examined an equilibrium study of a rumor spreading model according to propagation parameters and initial conditions. Furthermore, Huang [12] established two models for rumor spreading process with denial and skepticism. Recently, Zhao et al. proposed rumor spreading models in social networks considering the forgetting [13] [14] and refuting [15] mechanism of spreaders. Moreover, Zan et al. [16] examined the dynamics or rumor spread with counterattack mechanism and self-resistance parameter. Huo et al. [17] investigated the psychological effect with rumor spreading in emergency event. In addition, Afassinou [18] analyzed the impact of education rate on rumor final size. Zhao and Wang [19] established a dynamic rumor model considering the medium as a new subclass. Later, they refined the model by adding another subclass for government measures to control rumor propagation [20] . Also, they examined a model of information transmission with isolation [21] . Zhao et al. investigated a rumor model by extending a new class named hibernators. This class refers to spreaders who enter it due to forgetting mechanism and later leave it to become spreaders again due to remembering mechanism. They studied the model in homogeneous [22] and inhomogeneous [23] networks.

The above rumor models do not consider the fact that an individual may take time before accepting or rejecting what they hear or read. Some individuals think about rumors for some time before they become spreaders or stiflers. This period is called rumor incubation time. Huo et al. [24] introduced incubation class in studying rumor spreading model. They assumed that ignorants (susceptibles) entered first incubation class as a result of spreader and incubator contact. After some time the incubators become either spreaders or stiflers. But they overlook the option that ignorants may move directly to the spreader class. They examined qualitatively the limiting dynamical system of the model. Later, Chen et al. [25] proposed another rumor transmission model with latent class. They assumed that ignorants might move at first to three classes: latent, spreader and stifler. However, the possibility that latents may move to stifler class after the latent period is ignored in the model. They also qualitatively studied the limiting system of the model. In this paper, we propose a rumor propagation model with incubation mechanism that accommodates for both possibilities: incubators move to stifler class and susceptibles move to spreader class. In reality, not all individuals seek more information to ascertain the validity of a rumor before spreading it. At the same time, when some individuals do seek authenticity of a rumor, they may find it false or not worth spreading. Our aim here is to investigate the full dynamics of the model system using qualitative theory to have a better understanding and acquire more insight on the key parameters for controlling the dissipation of rumors. The rest of this paper is organized as follows. We describe the formulation of the proposed rumor transmission model with incubation mechanism and examine the existence of equilibriums and basic reproduction number in Section 2. In Section 3, we analyze the model system qualitatively and derive the local and global stability conditions for the equilibriums. In Section 4, we illustrate numerical simulations of the model and discuss the parameters that have impacts on the cessation of rumors. Finally, a brief conclusion is given in Section 5.

2. Mathematical Model

We consider a variable population size at any time t and denote it by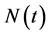. We divide the population into four disjoint classes of individuals: Susceptible, Incubator, Spreader, and Stifler denoted by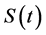, , , and, respectively.

The susceptible class, describes people who have not yet been exposed to a particular rumor. The incubator class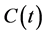, refers to people who are thinking about the rumor, but has not taken any action towards it. The spreader class, refers to people who take an active interest in the idea or concept that a rumor represents, and therefore have a tendency to talk about the rumor in social interactions. The stifler class, indicates people who have experienced the rumor, but have no interest or have lost interest at some point. The mathematical model is illustrated in the transfer diagram (Figure 1).

As shown in Figure 1, the dynamics of the model are based on the following assumptions. The rumor is constant, that is, the same rumor is being propagated throughout the classes at all times. Individuals are recruited through the susceptible class and it occurs at a positive constant B, namely immigration constant. They leave each class at the same emigration rate,. A susceptible know about the rumor when contacting a spreader at a rate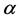, namely transmitting rate, where 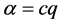such that c is the average number of contact per unit time and q is the probability of transmitting the rumor. After knowing about the rumor from a spreader, some susceptibles with probability experience an incubation period and move to incubation class. However, other susceptibles with probability believe the rumor and start spreading it immediately without any confirmation and move to spreader class. During the incubation period, the incubators try to think about the rumor and acquire more information to decide whether, on the one hand, the rumor is valid or not, and on the other hand, is it worth spreading or not. Based on the incubators judgement, they either move to spreader class at a rate, namely spreading rate, or move to stifler class at a rate, namely stifling rate. At any time, a spreader may lose interest in spreading the rumor, as a result becomes a stifler at a rate, namely removed rate. All rates are positive constants.

Taking the above considerations, the model is described according to the dynamic theory by the following nonlinear system of ordinary differential equations:

(1)

Note that. It follows from system (1) that which can be solved easily to give where and therefore, . Thus, the considered region for system (1) is

The vector field points into the interior of on the part of its boundary when Hence, is positively invariant, i.e., every solution of system (1), with initial conditions in remains there for all.

To find the equilibriums of system (1), we set the rates in (1) to zero:

(2)

(3)

(4)

(5)

The model has a rumor free equilibrium if there are no spreaders and no incubators, that is, , which means that the rumor dies out. By solving Equations (2)-(5), we find that the rumor free equilibrium is. Before obtaining the other equilibriums, we first find the basic reproduction number using the method of next generation matrix [26] . Here is defined as the expected number of secondary cases of rumor spreaders produced by a single spreader. The basic reproduction number plays a significant role when designing control intervention for a system. Let then system (1) can be written as:

where

The Jacobian matrices of and at the rumor free equilibrium point, are

where

and.

Thus the next generation matrix is Hence, the basic reproduction number of system (1) is the spectral radius of matrix, that is,

Next, we solve Equations (2)-(5) to find a positive (rumor existence) equilibrium of system (1). From Equation (2), (3) and (5) we find that:

Substituting for and in Equation (4), we get:

The non trivial root of the above equation is: In terms of the basic reproduction number, is rewritten as:. So, if, then which means that does not exist biologically.

Theorem 1 System (1) has two equilibria: the rumor free equilibrium which exists always; and the rumor existence equilibrium which exists if.

3. Stability Analysis

3.1. Local Stability

Here we investigate the local stability of and using linearization method [27] and matrix analysis [28] . We state the following theorems:

Theorem 2 (stability of E₀) If and, the rumor free equilibrium point is locally asymptotically stable. If and, is locally stable. If, is unstable.

Proof. Linearizing system (1) (by linearization method [27] ) we obtain the Jacobian matrix evaluated at the equilibrium:

Clearly the eigenvalues of the characteristic equation [28] are: and satisfy the equation

(6)

where,

Based on Routh-Hurwitz Criteria [28] , Equation (6) has two negative eigenvalues if both and. If, that is, Then also . Now, if, then

Simplifying, we have:

Therefore, if and, then and the eigenvalues have negative real parts. So, all eigenvalues have negative real part if and, and hence, is locally asymptotically stable. If and, then and, thus is locally stable. If, then, therefore is unstable.

Theorem 3 (stability of E^*) The rumor existence equilibrium is locally asymptotically stable if

Proof. Linearizing system (1) at the equilibrium gives

The eigenvalues of the characteristic equation are: and satisfy the equation

where,

From (4), since Moreover, if Therefore, Now,

If then. Hence by Routh-Hurwitz Criteria [29] have negative real parts if Thus, all eigenvalues of have negative real parts. Consequently is locally asymptotically stable.

3.2. Global Stability

First, we explore the global stability of. Consider the Lyapunov function [30] : Since, then and we have, if. Moreover, since is non-negative, it follows that if; with if and only if.

Hence, the only solution of system (1) in on which is. Therefore, by LaSalle’s Invariance Principle [30] , every solution of system (1), with initial conditions in, approaches as. Hence, is globally asymptotically stable and we can state the following theorem.

Theorem 4 (stability of E₀) If then is globally asymptotically stable in.

Next, we examine the global stability of. Consider the Lyapunov function [30] :

Here, we used. Hence, is globally stable and we can state the following theorem.

Theorem 5 (stability of E^*) The rumor existence equilibrium is globally stable.

We summarize the result of this section as follows:

• If and, then is locally asymptotically stable. If then is globally asymp- totically stable and in this case does not exist.

• If then is locally asymptotically stable. It is globally stable unconditionally whenever it exists.

4. Discussions and Simulation

In this section, we illustrate numerical simulations of system (1) to support the qualitative analysis. Furthermore, we examine key parameters that may contribute in controlling the spread of rumors.

Numerical simulations of system (1), with different initial conditions, show that the rumor disappears at an equilibrium level when and (Figure 2). However, the rumor persists at an equilibrium level when (Figure 3).

In reality, rumors prevail if there exist many spreaders. Therefore, It is clear that the parameters: and in system (1) may affect the size of the spreader class. To have a better understanding of the role of these parameters, we carry out numerical simulations by varying only one parameter to see its impact on the spread of a rumor. These investigations give more insight on useful management strategies to control the dissipation of a rumor.

By varying the transmitting rate and holding all other parameters at a fixed value, we can see in Figure 4 the changes in the size of the spreader class over time. It is clear that the lower the transmitting rate, the smaller the size of the spreader class. With a lower value, fewer susceptibles become spreaders and incubators. This means that the chances of a spreader having contact with susceptibles is small. Therefore, the

transmission of a rumor becomes difficult. This implies that governments should impose laws with strict punishment as a control measurement to stop the transmission of rumors in order to preserve the stability of a society.

Figure 5 demonstrates how the size of the spreader class changes with time by varying the probability parameter and fixing all other parameters. If is large, then the probability of susceptibles becoming incubators is greater than the probability of becoming spreaders. As shown in Figure 5 the higher the probability parameter, the smaller the size of the spreader class. With a higher value, fewer susceptibles become spreaders. This means that the incubator class is a significant cause of decreasing the number of spreaders. In other words, acquiring more information about a rumor before deciding to take any action minimizes rumor dissipation. This indicates that increasing public awareness towards the importance of thinking before speaking is an essential strategy to control rumor spreading. In addition, awareness towards the role and responsibility of individuals in dealing with rumors is of great benefit to the society.

Figure 6 illustrates the changes in the size of the spreader class over time with different values of the stifling rate, while holding other parameters fixed. It is clear that the higher the stifling rate, the smaller the size of the spreader class. With a higher value, fewer incubators become spreaders. The increase of the stifling rate depends on the incubators’ scientific knowledge during the incubation period. If incubators have logical reasoning, then it is easy to discriminate a rumor. On the other hand if not, then more information must be available for incubators in order to reach a good judgement. This implies that the incubation period is crucial to crack down a rumor. Therefore, a powerful strategy to cease a rumor is to release information with logical facts about it. For this strategy to be effective it must be carried out as soon as a rumor starts to circulate.

5. Conclusion

In this paper, we formulated a rumor transmission model with incubation period, constant recruitment and varying total population. The model accommodates for both possibilities: incubators move to stifler class and susceptibles move to spreader class. The full dynamical system of the model is studied qualitatively producing two equilibrium points: rumor-free and rumor-existence. The existence conditions of the equilibriums are investigated. The rumor free equilibrium exists always, whereas the rumor existence equilibrium

exists only if. The local and global stability analysis of both equilibriums is examined. We find that

is locally and asymptotically stable if and, and is globally and asymptotically stable if. Moreover, is locally and asymptotically stable if, and is globally and unconditionally stable whenever it exists. The results of the numerical simulations are found to be in good agreement with the qualitative analysis. In other words, a rumor terminates when and and prevails when. The impact of different management strategies on the dissipation of rumors is analyzed numerically by varying key parameters in the model. It is found that the number of spreaders is minimized if the transmitting rate is small and both the probability parameter and the stifling rate are large. Consequently, some effective strategies for rumor disappearance are: strict laws imposed by govern- ments, public awareness towards thinking before speaking, and the immediate release of information with logical facts about a rumor.

Cite this paper

Salma Al-Tuwairqi,Sarah Al-Sheikh,Reem Al-Amoudi, (2015) Qualitative Analysis of a Rumor Transmission Model with Incubation Mechanism. Open Access Library Journal,02,1-12. doi: 10.4236/oalib.1102040

References

NOTES

^*Corresponding author.