Received 17 October 2015; accepted 1 November 2015; published 6 November 2015

ABSTRACT

The fully Unified Theory of {Strong, EM, Weak, Gravity} interactions all arising from the unique source of electronic charges has been established. The theory proves that the Nature is astutely simple in essence, and the most of the recently promoted circuitous physics seem to be incorrect in the new light. In the proposed theory, the 100% of matter and energy content of the Universe, including the dark matter and energy, is predicted in terms of a single integer parameter L in one-to-one agreement with the observation. To boot, the {Z, W} bosons are proven to be compound states with their innate heavy masses; they never have been zero-mass particles, and the Higgs boson is uncalled for. The unified theory also has explicated the ever mysterious strong interaction number “137”, and leads to QQD (Quantum Quark Dynamics) parallel to the QED. The QQD gives, for example, very simple explanation of “Asymptotic Freedom” without requiring the unwarranted and arduously complex QCD.

Keywords:

Unified Theory of Everything, Origin of Masses, QQD, Asymptotic Freedom

Subject Areas: Particle Physics, Theoretical Physics

1. Introduction

In this paper, all four {strong, EM, weak, gravity} interaction forces are unified―the major goal of the modern theoretical physics―to arise from the unique source, the electronic charges. The physics of the {gravity, EM} stretch forth into the open space-time of the Universe, while the strong interaction quantum entangles in the spherical curved space-time in the diminutive particle holes. The overall unification of the interactions thus requires revolutionary insights into the strong interaction physics of which contrivances were so forbiddingly difficult to understand that the great Niels Bohr once stated that all those ideas for the cues were not crazy enough [1] .

In fact, because of the inordinately disparate nature of the strong interaction, the experimentally determined fine structure constant “137” that characterizes its interaction strength has long been considered to be beyond the human comprehension [2] . For example, the great Richard Feynman lamented, “Nobody knows. It (‘137’) is one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the Hand of God wrote that number, and we don’t know how He pushed His pencil” (also see §6). However, in terms of the fully Unified Theory in this paper, all aspects of physics are simple and kindred in essence, and the seminal number “137” is easily derived through the exploration of the Quantum Quark Dynamics (QQD) in parallel to the QED (see Equations (18) and (18a)). The great scientist was right; it shall be shown that the primary essence of the strong interaction physics is dexterously embedded in this QQD number, enabling to apprehend the sequestered interaction by the ab initio nuclear physics in parallel to QED (see §3, §6, and §10).

As the integer electronic charge “e” generates its definitive individual QED force, the fractionally charged quark shall be shown to generate its own similarly individual QQD specific strong interaction force. An incidental production of (virtual) quark pairs with their fractional charges dramatically increases the strong interaction QQD force inside the nucleons, and generates the highly bizarre phenomena of “Asymptotic Freedom” in the strong interaction (see §10). This renders the QCD―burdened by a number of assumptions that are unwarranted, including the color force that has never been defined mechanically, and for which no observational evidence exists―unnecessary.

The unification of the EM (of zero-mass photons) with gravity (of zero-mass gravitons) was the great Einstein’s praiseworthy, yet ultimately futile aspiration for the last 30 years of his life. Moreover, the general relativity does not give any explanation for the origin of mass. This formidable task has been accomplished earlier by this author [3] , where, while the EM as usual is the linear (both attractive and repulsive) manifestation, the gravity and the strong interaction force (see §3) are the quadratic (always attractive) revelations of the electronic charges.

All elementary particles of the Standard Theory are peremptorily point particles without any internal structure and innate masses, whose premise has proved false by the recent observation of the “Proton Radius Crisis” (see §13). In the unified theory, in contrast, all elementary particles have systematic substructures identified and distinguishable in terms of a single consecutive integer number L = 1, 2, 3, ∙∙∙, predicting one-to-one agreement of the 100 percent matter and energy content of the Universe [3] . This includes the 5% portion of the asymmetric visible matter and energy content as well as the invisible dark matter and energy that constitute the 95% portion of the Universe [4] [5] . All along, the Higgs physics is never required. The field generated by the mass and energy in the unified theory fully upholds the Einstein’s General Relativity; the gravitation behaving the same for all observers as the mass tells the space how to curve, and the space in turn tells the matter how to move.

Through the all-inclusive prediction in astonishing agreements with the entire observed spectra of elementary particle masses by the unified theory, the Higgs physics is never required. Moreover, the mass spectra for the {quarks in Table 1, Leptons in the Table 2} in this paper (see §4) shall prove to be like the microscope, the upended Galileo’s telescope, the simple contrivance that helped―despite the fierce rebuttals and prosecutions by the so-called authorities in that dark period of history―demolish the theory of geocentric solar system.

The unified theory of mass level microscope in this paper indisputably proves that―unlike the elementary gauge bosons of zero-mass {gluon, photon, graviton} for the {strong, EM, gravity} interactions―the {Z, W} bosons really are the compound particles, perforce ingrained with the extraordinarily heavy innate masses that have been accurately predicted in this paper in one-to-one agreement with experimental observations also without the Higgs physics (see §4, §7, and §8). The {Z, W} bosons never were zero-mass bosons, unequivocally rejecting the need of Higgs boson! This is a critical wake-up call revelation.

Moreover, the “Grand Unified Theory” in the conventional theory―an intermediate step that puts aside the most cryptic gravity―instead of simplifying the physics, makes it greatly more complicated, an ultimate catastrophe [6] . Many in fact are afraid that the long cherished and earnestly pursued ongoing modern physics has reached its inevitable “dead-end” [7] .

In contrast, the nature in the “Unified Theory of Everything” in this paper has proven to be astutely simple in essence, yet it puts the entire spectrum of physics neatly in harmony, enabling explicating the all-inclusive working mechanism of the Universe. The celebrated Einstein’s criterion in 1951 was that “If you can’t explain it simply, you don’t understand it well enough”. The criterion is decisive: the unified theory in this paper ascertains that the highly hyped Higgs physics and QCD that are promoted by craftily complex conjectures in fact are false to be rejected.

2. Universal Dispersion Constants

The Planck Constant, ћ, is introduced in the main to establish the photon (EM) quantum physics, deciding its energy. But, in terms of the EM fine structure constant, α_em, the same constant can carry out a dual role in terms of quantum tunneling as the universal EM dispersion constant in the unified theory [3] by

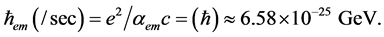(1)

Because all interaction fields in the unified theory arise from the electronic charges, the corresponding universal gravity dispersion constants with its fine structure constant, α_gr, are determined to be [3] ,

. (2)

With the strong interaction fine structure constant α_st = 137α_em, the universal strong interaction (gluon) dispersion constant is

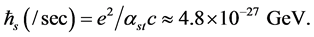(3)

The universal weak interaction dispersion constant would now result ad interim from its relative fine structure constant α_weak = O(10^-5α_s) to be

,

establishing rightward the dramatically increasing series of universal dispersion constants,

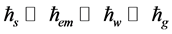. (4)

The Universe is stretched out and filled with multiple constituents: elementary particles, stars, and galaxies to the vast macrocosm. And the varying strength of the universal dispersion constants in Equation (4) perform a crucially important roles in terms of the relative quantum tunneling probabilities through the milieu, which can be estimated by the intrinsic exponential factor in WKB approximation [8] , i.e.,

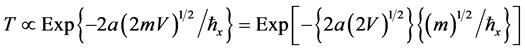, (5)

specified by the universal dispersion constant ћ_x in the unified theory, and the effective quantum partition potential V of width “a”, and the potent mass “m”.

The negative exponent is weighed by 2 factors: 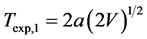and.

The physical parameter values here are not well determined, and the descriptions are only meant to provide a provisional overview of the vast complex of the Universe. Note that the first factor, T_exp,1, divides the Universe into two categories: (A) large scale subject like the black hole, and (B) the infinitesimal scale subject like the elementary particles. The second factor, T_exp,2, then divides and casts light on the specific quantum tunneling capacities for the apt subjects:

1) Case of large T_exp,1: While the gravity (of radically large ћ_g) can leak out with “T → 1” from the black hole, the EM (of much smaller ћ_em) is confined in it with “T → 0”, making the black hole invisible. Because of the huge ratio of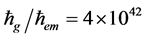, the determination is not much sensitive to the value of “”. The physics may also explicate the puzzle of dark matter and energy in the dual Universe [4] [5] ; the dark matter gravity in the dark Universe freely penetrates into the visible Universe in T = 1 to help regulate not only the galaxies, but also the clusters of galaxies, while the dark EM energy are trapped there in T = 0 as an invisible scalar energy to cause the accelerating expansion of the Universe.

2) Case of small T_exp,1: Shifting leftward in Equation (4), the elementary particles arises in self-similarity physics in metaphor of black holes. While the EM field of the small ћ_em of QED―with “aV^1/2” manifesting the surface effect of the extremely small nucleon hole radius O(r_e)―leaks out of the nucleon hole in “T → 1”, the fractionally charged quarks inside the nucleon (of quarkness = 3) with categorically small ћ_s (in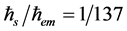) for the QQD strong interaction―more as a volume effect―are confined inside the particle holes in ultimate “T = 0” [see §3 & §6]. Nature is not only simple in essence, but also remarkably astute in the designing of the Universe, creating the black hole and the particle hole by the same baggage-free mathematical blueprint.

3. Quantum Entanglements for Quantum Quark Dynamics

In the unified EM-gravity theory [3] , the substructures of quarks and leptons are composed by multitudes of compacted (negatively charged) electron (positively charged) positron pairs in lattice structures. With the manifold compacted electronic charge pairs in the substructures, the quarks and leptons must be flooded with the potent EM field; the internal complexes of the quarks and (charged) leptons are perpetually batched plasma states The plasma state exhibits a strange entangling behavior even in the classical laboratory experiments, tending not to conform to external influences; it often behaves as if it had a “mind of its own” [9] . It has also been asserted that, in the realm of quantum entanglement, a large number of undulating quantum characteristics can be put together [10] , emerging in distinctly simple attributes [3] . Although the physics of quantum entangling strong interaction physics is not yet fully explored, its physical contingencies in terms of the unified theory appear to be unmistakable.

The EM force arises in terms of the quantized integer charges, interacting in the Coulomb force between two charges {Q₁ = (n₁e) and Q₂ = (n₂e)} (linearly) attractive and repulsive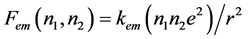, which is valid only in the flat space [11] . The literal analysis of the interaction force in the curved spherical space inside the particle hole for the fractionally charged quark would be very nebulous and complicated. But the unified theory is simple in essence, and the ultimate recipe of this strong interaction might also be simple as well after all.

The conventional EM Coulomb force formula for the two fractional quark charges {Q₁ = q₁e(q₁ < 1) and Q₂ = q₂e(q₂ < 1)}, 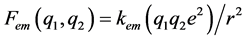, not only would not be valid in the curved spherical space of proton, but it also generates forces even smaller than the corresponding EM force with integer charges, i.e., 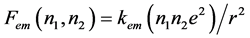, which itself is much smaller than the observed force for the strong interaction.

In the unified theory, both the EM and he gravity arise directly, or through the substructures, from the constituent electronic charges ( [3] , also see §4), and the strong interaction, in nature’s ingeniously unpretentious design, could follow the suits, also arising from the constituent quark electronic charges (q₁, q₂), keeping up the essentially same Coulomb mathematical form in the nucleon. The interactions in the unified theory thus progress from

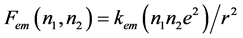for the EM interaction,

to 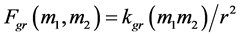for the gravity of apt quantum entanglement, (6)

, for the strong QQD interaction,

where of QQD that can generate much larger force than F_em(n₁, n₂) of QED. The “r_t” for QQD― pending a further exposition―represents the purported quantum entanglement truncated strong interaction radius with a very short range extent, perhaps, in a Yukawa potential-like exponential decrease.

The quarks in the proton {u, u, d} would interact in pairs of {u with u, u with d, and d with u} (see Figure 2), that is all in all {twice u with u, once d with d}, the total systematic force inside the curved spherical space of the proton hole would be rounded up in quantum entanglement of,

(7)

in terms of multiplication of the inverse square of the fractional quark charges inside the truncated radius r_t in QQD, not in addition. Equations (6) exhibits the pretext of the unified theory, and its application by Equation (7) to the nucleons {proton, neutron} of 3 fractionally charged quarks conspicuously produces the long searched fine structure constant value “137”, verifying the QQD (see §6).

On the other hand, the quantum entangling strong interaction force confined in the curved spherical particle hole would seek a quantum harmony embracing the Universe, summing up the fractional quark charges into the EM integer values. Along with this operandi, the 3 fractionally charged quarks with spin = 1/2 become aligned to form aninteger charged fermion of spin = 1/2, and may mimic the complex description of “charged quark color” symmetry [12] that is proven to be uncalled for in terms of the QQD.

4. The Particle Masses [See the Footnote]

The quarks and leptons have quantum entangling inner substructures, which are formed in terms of lattice substructures of compacted electronic pair charge bits of Q_c = q_ce, where, respectively, for the {quarks, leptons} with the compacted radius that generate the EM force (in cgs unit),

(8)

The quark masses in the unified theory, are thus determined [3] by

, (9)

predicting those in Table 1 in close one-to-one agreement with the observed values for the {u, d, s, c, b, (Z, W), t} quark based states in term of ℓ = 3 × (2L) with the sequential integer L (see §7 and §8).

The number of lattice substructures of compacted fractional electronic charge bits of is determined by

(10)

The sphericity parameter B_s in Equation (9) and (10), or the cubicity parameter of, varies appropriately within 1 (for full sphere approximation) > B_s > π/6 (for full cube approximation). The B_s here varies linearly to represents the increasingly complex substructures with the linear parameter ℓ.

The lepton mass formula [3] ,

(11)

predict the (e, µ, τ, {W, Z}) states in Table 2 (see §7 and §8) again in close one-to-one agreement with the observed values. The number of the lattice substructures is

, (12)

for the ℓ = 4L states for the charged leptons, while ℓ = 3L for the {Z, W} bosons with the sequential integer L.

The {Z, W} states in Table 2 thus swerve to ℓ = 3L variation in the high mass states, making connection to the {Z, W} states in the Table 1 that entirely vary in ℓ = 3 × (2L). As the ℓ increases to these levels, the structural alterations become necessary for their stability (see §5 and §7), and the {Z, W} states convert to spin = 1 bosons both in Table 1 and Table 2, instead of being the intended spin = 1/2 {quark, lepton} fermion states.

In spite of the rapid increases in the number of constituent substructure charge bits, N_f and N_w, with the consecutive climb of the integer L, the emerging one-to-one agreements between the predicted and observed masses shown in Table 1 and Table 2 are in astonishing exactitude [13] . This is a major achievement in particle physics that has never been imagined possible. Moreover, the processes never require the irrelevant Higgs mechanism. The tables also exhibit a germinal dissimilitude for the {Z, W} states; because they really are composite bosons with their innate heavy masses (the discussions continue in §7 and §8)―which fact could not have been understood without the mass Table 1 and Table 2, where they correctly transfigure from fermions (quarks and leptons) to the bosons in response to the changing dynamical requirements.

Thus the Table 1 and Table 2 together in fact act like the microscope, the upended Galileo’s telescope (see §1). This is a very imperative revelation. Without this microscope, it is like once again looking up the sky bare-eyed, and see the earth-centered Universe, and the absurdity of zero-mass {Z, W} bosons would continue, propounding Higgs physics.

The leptons substructures with basic substructure charge q_c = 1 are simpler than those quarks with q_c = 1/3. The low {L} = {ℓ/4} = {1, 2} lepton states, for examples, straightforwardly and unequivocally predict the observed masses with large mass shift from m_μ = 107 MeV (for muon in terms of 53 compressed substructure charge bits) to m_τ = 1777 MeV (for tauon in terms of 431 compressed substructure charge bits).

Yet, the experimental observation of muon itself had been a great puzzle in the history of physics. The great Richard Feynman would in fact be stupefied to find m_μ =107 MeV predicted in the Table 2; the vexing mystery of large seemingly arbitrary lepton mass spurred him to inscribe on a corner of his Caltech blackboard: “Why does the muon have so much mass?” [14] . Also, Isidor Rabi quipped “Who ordered that… muon?” at its serendipitous and seemingly random appearance [15] .

Can any other theory predict the {µ, τ} leptons―not to mention the entire quarks and leptons shown in the Table 1 and Table 2―as correctly as is done in this paper? No! The claim that Higgs physics determines the entire elementary particle masses is an outright lie! The two great physicists (and this author respectfully joins them) would categorically reject any covertly waving of hands to mask their foible for its claimed role in the mass creation.

The physics of Table 1 and Table 2, by fully providing the electronic structure for the determination of elementary particle masses, unified the gravity with the EM interaction. It shall also be shown (see §6) that the EM of QED and strong interactions of QQD arise from their specific electronic charges to unify the strong and EM interactions, establishing the long searched “Unified Theory of Everything”.

The novel theory can also account for the origin of the dark matter and energy, explaining the entire content of the Universe [4] [5] . The gigantic gamma ray bubbles emerging from the Milky Way Galaxy core, which according to existing astrophysical theories shouldn’t be there, for example, are also anticipated phenomena in terms of the unified theory. In the imminent grit, on the other hand, the EM origin of mass in this paper implies the celebrated relation E = mc².

The validity of a theory is determined by its capability of explaining the physical structures with predictions in agreement with experimental observations. It is well known that the Standard Model in contrast is far from complete, and the Higgs boson mass that determines Fermi Scale is not yet established. This is a serious deficiency [15] ; Higgs physics cannot predict the particle mass levels. Instead, each state mass is achieved post hoc using an arbitrary coupling parameter that is determined from the experimentally observed data. When CERN discovered the particle believed to be Higgs boson in 2012, it declared the Standard Model of particle physics complete. Many―only meekly―questioned the conclusion, and now the Higgs physics itself is determined to be unwarranted.

5. W-Boson Transformation

The quarks in Table 1 emerge in the parameter series of “ℓ = 3 ´ (2L)”with a primary multipier of “3”. And so do the {Z, W} bosons with 2L = 2 ´ 6 = 3 ´ 4. The lepton in Table 2, on the other hand, emerge in the parameter series of “ℓ = 4L” with primary multiplier of “4”, but switch over to the parameter series of “ℓ = 3L” with the primary multiplier “3” for the {Z, W} bosons of “L = “3 + 4”. This suggests that the {Z, W} bosons (with EM charges of {1, 0}) may transpose from the quark-like substructure in the Table 1 to the lepton-like substructures in the Table 2 as shown in Figure 1, or in reverse direction, to unify the strong interaction with the weak interaction via EM interaction.

The W bosons transform to the quark-antiquark pairs by 68%, against the leptonic decay of only 32%. And the leptons emitted in the beta decay did not exist in the nucleons before they were created at the instant of decay. Thus, the W bosons might not be full weak interaction mediators. The uncertainty principle lifetime of the (virtual) W boson in terms of guileless weak interaction constant ћ_w [of Equation (4)] is estimated to be t_w = O (3 × 10⁻²⁵ second). But the observed beta-decay lifetime of O (900 second) is far too longer without any off-the-rack explanation. It is possible that the beta decay in fact undergoes the transition from the quark-like to the lepton-like W boson, and the small m_d − m_u = 2.5 MeV as compared with greatly larger m_W = 80,000 MeV could tame the quark-lepton transition to enable the greatly longer beta-decay lifetime.

The transformation speed could thus be situation dependent―even depending on the temperature [16] ―to cause the variations to the decay strains and times. The epitome observations have in fact been realized recently [17] through two different―beam and bottle―experiments that gave different neutron lifetimes. The statistical significance of the discrepancy for the two experimental techniques has been determined to be unlikely a random anomaly, indicating that the W boson in the beta decays in fact undergo hiatus transformations that are situation dependent. This finding is possibly as significant as the once bewildered “asymptotic freedom” and “proton size puzzle”―but all discomposure can be explained in this paper (see §10 and §13)―indicating the relevance of the transformation mode shown in Figure 1.

Another whimsy here is that a weak interaction lapse (if at all) in the black hole [18] might grow the long speculated sporadic hair on it through the weak interaction universal dispersion constant cleft of ћ_em (for T = 0) < ћ_w < ћ_g (for T = 1). Moreover, the matters in the dark side of the dual Universe could copiously produce the high energy neutrinos in the weak interaction, and they could also leak into the observable Universe in terms of the ћ_w (>ћ_em) while impounding the EM, explaining the puzzling dispersed origin of the high energy cosmic neutrino observation.

6. Strong Interaction in QQD

The equations of state vary depending on the nature of the EM field and, according to the Friedmann Equation [19] , the radiative pressure can be determined by

, (13)

where ω_x is the equation of state, while the ρ_rad,x represents the constituent radiation energy density.

The equation of state for the vector EM radiation ω_em ≈ 1/3 gives

(14)

while the equation of state ω_de ≈ −1 for the scalar dark energy yields,

(15)

to make the Universe expand in acceleration as observed [4] [5] .

The strong interaction equation of state for the proton p(u, u, d), ω_st,p, would be determined by the quantum entangled fractional quark charges, Q_u = 2e/3 and Q_d = −e/3, in the curved spherical particle holes. The task is very simple in terms of QQD (see §3),

in total proton EM charge of. The radiation pressure force for the strong (gluon) field thus is

(16)

If the origin of both the strong interaction field of QQD and the EM interaction field of QED are the same electronic charge distribution inside the nucleons, that is

, (17)

as proposed in the unified theory of this paper, giving

(18)

from Equations (14) and (16).

The neutron would be tempered by the virtual W⁻ bosons,

with Q_u + Q_u + Q_d = +e, and Q(W⁻) = −e. If the neutron is bound, the virtual W⁻ would remain quark-like state, coursing back to

If the neutron is free, exposing the W⁻ boson to the capacious surface volume and transfer (see Figure 1) to the lepton-like state, it may suffer the beta decay through

The neutron constantly fluctuates to a “proton +” in nucleon and the neutron equation of state, ω_st,n, is practically the same to the proton case to have ω_st,n = ω_st,p = 45.56 in QQD with the total neutron EM charge of. This gives the same strong interaction force both for the neutron and the proton, i.e.,

(18A)

The Equations (18) and (18A) have thus deciphered the origin of the interaction strength ratio between the QQD and QED. Moreover, the Equation (17) reveals the vital understanding that the source of the strong and EM interactions are the same electronic charges in the particle holes, making all interaction fields arise from the electronic charges [3] to accomplish the “Unified Theory of Everything”. The Equations (18) and (18A) fully prove that the genesis of the quark strong interaction QQD in fact is in parallel to the QED with the fractional quark charges {q₁, q₂} (see §3).

Magnetism plays an important role in producing energy in nuclear fusion reactors. It is rather arresting to note here that the magnetism originates from electricity, and the matter in a “magnetic bottle” at very high temperature―in a way like the quarks in the nucleon hole―can exist as charged particles in the center―strongly held by the magnetic field away from the container’s wall.

The Equations (18) and (18A) would have flabbergasted many great founders of modern physics: Sommerfeld, Eddington, Born, Pauli, Dirac, Weyl, Heisenberg, etc. [2] . Beside Feynman (see §1), the great Werner Heisenberg, had proclaimed that all the quandaries of quantum mechanics would shrivel up when “137” was finally explained (see pp 8-9 of [1] ) as is done in this paper. The great Wolfgang Pauli would agree; this paper had delivered the explanation to his perpetual puzzle about which he had to ask about to none other than the creator God himself in the Heaven (an allegory), “Why is alpha equal to one over one hundred thirty-seven?” (see pp 8-9 of [1] ).

The EM and gravity have their specific charges {electric charge and charge-originated mass}, and exhibit their own specific forces in F_em(n₁, n₂) and F_g(m₁, m₂). The number “137” proves to be the indispensable key that help decipher the QQD strong interaction force F_st(q₁, q₂) for fractional charge {q₁, q₂} in parallel to F_em(n₁, n₂) and F_g(m₁, m₂). This is very reassuring to realize that the Nature in the Unified Theory of Everything has been written by the same baggage-free mathematic blue print.

With the development of the QQD in this paper with the negligible universal dispersion constant, ћ_s, the hypothesis of “color force”, where the “color” has never been defined mechanically, becomes entirely unnecessary. The QCD in fact has raised a bevy conundrums [19] ―such as why some particles have colors, constantly changing from one to the other (indicating its individual strength is quixotic), while others lack it and are thus “color-blind”. Neither is the question of how colored quarks and gluons combine to make colorless hadrons is really clear (see §10).

7. Formation Requirements

It shall now show that the unprecedented accurate mass predictions in the microscopic Table 1 and Table 2 for the quarks and leptons in one-to-one agreement with observation can also explain why they are restricted to the 3 generations of {u, d; s, c; b, t} and {e, ν_e; µ, ν_μ; τ, ν_τ} states. Moreover, the predictions include the {Z, W} bosons that shall be proven to be the composite particles with the observed large innate masses that reject the need of Higgs boson.

The fundamental substructure elements of the quarks and leptons are the compressed electronic charges of {q_ce} = (±){e/3, e} by a compaction parameter ℓ. The substructure charges generate the local EM repulsive force given by Equation (8), countering the compressive QQD gluon forces in quantum entanglement, thus providing the basic formation criterion in QQD for all the leptons and quarks by a single (and simple as well) requirement,

. (19)

For the quarks with q_c = 1/3 and {ℓ} = {3 ´ (2L)} for {L} = {1, 2, 3} states starting from the ℓ = 3 ´ 1 primary states of the {u, d} quarks, Equation (19) reduces to

, (20)

producing the stable {(u, d), s, c, b} quark states, a remarkable achievement that in fact vouch for the correctness of the mass formula Equation (9).

With fractional charge q_c = 1/3 in quantum entanglement for the great numbers of substructure charges in the particles, the basic substructure force may begin to overwhelm its up keeping force at midway Lup, and make certain adjustments. For example, the basic effective charge q_c may switch in quantum entanglement to 2/3, that is,

for the L = 4 ( or ℓ = 24) state,

and

for the L = 5 (or ℓ = 30) state,

where upon, if the states continue to be self-sustained, the states would become volatile.

The {Z, W} states of L = 6 in Table 1 [together with the extremely heavy t-quark of L = 7 state (see §8)] seems to require a conspicuous tweaking to counter the developing instability in

for the L = 6 state with q_c = 1/3.

In point of fact, 144 is close to 137, and the quark substructures number in quantum entanglement in L = 6 state, N_f = O(45,000), is so large that they might just linger on, and split into two equal self-possessed parts in quantum entanglement, each with “spin = 1/2”. The two spins {s₁ = 1/2 and s₂ = 1/2} then not only could add to turn the mode into the spin s₁ + s₂ = 1 composite boson state, but also the resultant state in quantum entanglement could be adjusted into the boson specific integer {1, 0} charges.

Thus, pending further analysis, the L = 6 (or ℓ = 36) {Z, W} composite boson states would achieve a transitory stability with the disjunction parameter d_p = 2 (see Table 1 and Table 2),

.

The {Z, W} boson states in Table 1―supposedly “spin 1/2” quarks (fermions), turning into the “spin 1” dually composite boson states―clearly demand this tweaking. And the {Z, W} states―the substructure compound states―do maintain the hefty innate masses and the boson specific integer EM charges to lose the quark specific disposition of gluon force. Thus the {Z, W} boson have never been innate zero-mass states, and they never require the Higgs bosons to acquire their masses. The Higgs physics is absolutely out!

This proposition is further proven to be true with the following surprising observation:

where the angular momentum conservation seems to be violated. But it didn’t! According to the d_p = 2 splitting, besides the s₁ + s₂ = 1 state, the proposed dual spin state (of s₁ = 1/2 and s₂ = 1/2), should also generate the s₁ + s₂ = 0 spin state as well, providing,

The W boson of dual spin = {1, 0} is factual, confirming the authenticity of the d_p = 2 tweaking for the W-boson.

For the primary leptons with q_c = 1 and ℓ = 4 L for {L} = {1, 2, ∙∙∙} starting from the ℓ = 1 basic state of electron, on the other hand, the Equation (19) reduces to

Since {ℓ}² = {1, 16, 64} < 137 for the cases of {ℓ} = {1, 1 ´ 4, 2 ´ 4}, the 3 generations of {e, ν_e; µ, ν_μ; τ, ν_τ} states are stable to be observable, in fact affirming the lepton mass formula Equation (11).

The lepton substructures with integer charge q_c = 1 in Table 2 are capable of forthwith leaking out of the particle hole by itself, and the condition of Equation (19) is decidedly required for the primary lepton formations. Thus, the leptons for the cases of L ³ 3 (or ℓ > 4L = 12),

cannot be durable.

It is seen that the primary multiplier factor “3” in 3 ´ (2L) for the quark-like {Z, W} boson was carried to the lepton-like {Z, W} bosons in 3L (see §5) with same multiplier “3”. Is it possible that the basic quark-like substructure pair charge, q_c = 1/3 is also carried on to the lepton-like {Z, W} bosons with the disjunction parameter d_p = 2 to attain the spin= 1 in quantum entanglement, i.e.,

The lepton-like W boson decays to one of the mass-carrying charged lepton {e, µ, τ}, allowing it to be accompanied by the (nearly) massless neutrinos in terms of the quantum entangling uncertainties.

8. The t-Quark and the X(125) State

The ability of transmuting the innate fermions to composite bosons of disjunction parameter d_p > 1 is a defining development for the unified theory [20] . And the interjection of the disjunction parameter d_p = 2 state above may not be a simple stopgap artifice to turn the {Z, W} particles to the {spin} = {1, 0} composite bosons. The transitory nature of the quarks in the Table 1 may further engender structural metamorphosis as the compaction parameter ℓ increases to further enmesh the substructure. In fact, for the ℓ = 3 ´ (2 ´ 7) (or L = 7) state―that contains the compressed substructure charge bits of O(73,000)―the complexity might gambol in quantum entanglement to increase the disjunction parameter to the triplicating d_p = 3 to uphold the state, that is,

With d_p = 3 along s₃ = 1/2, the t-quark state of s₁ + s₂ + s₃ = 1/2 is correctly restored back to fermion. With the three “1/2” spins consolidating into a single 1/2 spin, the state might simulate the three quarks in a nucleon hole (see §3), and decays without the hadronization in O(10E−22 second) because of its intrinsic stability.

(21)

With the further increase in the substructure number N_f (see Table 1), the sustainability of the L ³ 8 states would collapse, in fact limiting the quarks to the 3 generations of {u, d; s, c; b, t} states.

The unified theory in this paper (also see [3] ) unequivocally has predicted the X(125 GeV) of the ℓ = 3 ´ 13 state―a scalar boson in reflection of the vector boson {Z, W}―that stands notably deviant from other substructure states in Table 1. This predicted state X(125 GeV) must be real. It is understandable if such an off-beat state X(125 GeV) turns out to be very hard to be detected.

Ironically, the acclaimed Higgs boson had been observed at the very same mass level of X(125 GeV) after such an extraordinarily fervent hunt. If the Higgs field in fact provides milieus for all the masses in the Universe, on the other hand, the 125 GeV state would be highly discernible. In stark contrast, the Higgs boson persistently stays in the dark [15] as the X(125 GeV) state in Table 1 would. The Fully Unified Theory can predict 100% of masses, including those of dark matter, absolutely without the need of Higgs bosons. It is thus no surprise that the consensus on the 125 GeV state observed by CERN in 2012 has begun to shift that it is not really the acclaimed Higgs boson [21] [22] .

9. Nucleon Masses

The nucleons are constituted by 3 quarks; {u, u, d} for the proton, and {u, d, d} for the neutron. When the proton is bombarded by high energy electrons, the quarks inside it seem to act like free point-like scattering centers with their binding energy very small compared with the energy of the electron energy.

On the other hand, it has been shown [3] that all the free elementary particles, including the quarks, have their primary size of radius O(r_e). There is thus no guarantee that the spontaneous quarks inside the nucleon become so small in size that the 3 quarks can transpose freely as observed in asymptotic freedom. Moreover, the observed (free) constituent quarks masses add up only to O(10 MeV), while the gluons themselves are massless. Then, how the nucleon mass measures up to 938.2 MeV for the proton, and 939.5 MeV for the neutron, is still a great unsolved mystery in the conventional theory.

The Equation (8) indicates the quark mass dependences on their size, increasing upon compression. The (compressive) QQD gluon force in the nucleon hole is much stronger than the QED force in terms of the lattice substructure charges in the quarks. Thus, if the quarks are compacted inside the nucleon hole by the compressive QQD force, their masses can increase by the factors of compression parameter, C_x, which can approach O(137) in the particle hole, and move without getting in each other’s way. The quark pairs in the mesons also are compressed by QQD gluon force to attain their (pion) masses. The proposition is entirely consistent; the quarks appear to be additionally compressed in the excited baryon states due to the increased pressure generated by the asymptotic freedom and accordingly enhance their effective masses (see §10 and §12).

The compressive gluon forces would be more or less fagged out for compressing and bringing the quarks to their nearly free contour with their effective compression parameters {C_u, C_d} for the confined u and d quarks. The nucleon {p, n} masses can thus be approximated by solving two linear equations in the first order approximation [3] :

which give

(22)

with C_u/C_d ≈ 1.92.

Although C_u > C_d, the d-quark is a priori compressed harder by the factor of than the u-quark, and

The bound quark masses in the nucleon holes thus are,

(23)

greatly heavier than m_u ≈ 2.4 MeV and m_d ≈ 4.6 MeV as free quarks. The C_u and in fact are close, yet less than gluon compression force of Equation (18), proving the correctness of the mass formulas Equations (9) and (11). The quarks in the nucleon here would seem point-like with their small binding energy as observed.

The baryon masses in general―to the first order approximation―are thus in the main close to the sum of the compressed and thus greatly heavier constituent quark masses [3] , that is,

(24)

where C_qn represents the effective compression parameter for the possibly multiple compressed constituent quark masses, while M(s, l) arises from the potential spin and orbital angular momentum couplings. The correctness of this approximation Equation (24) has been thoroughly verified in the general application to the determination of the observed particle mass levels (for more examples, see §11 and §12).

In the conventional theory, with the trifling 1% mass coming from the three (free) quarks, the rest 99% mass of the nucleon mass is assumed to come from the interaction of gluons and quark-antiquark pairs (many as pions) in zillions that zip around near the speed of light, banging each other and appearing and disappearing within the nucleon hole, making their stability untenable and decipherable, if at all, only with the adroit supercomputers [23] . The Einstein’s criterion (1951) would not forgive such a grandiose complication and outright reject it.

10. Asymptotic Freedom

Although the quarks bound inside the proton seem free, it is not only impossible to strike them off the proton, but also the quark binding forces seems to increase upon perturbation, acting as if they are fastened by a rubber band that pulls them back stronger when they are pushed apart. These two contrasting aspects of behaviors― called asymptotic freedom―is an inevitably simple consequence of QQD.

The quantum mechanics allows, in fact requires―through a temporary violation of energy conservation―to generate the virtual particles. The proton, for example, would be inflicted by the virtual meson (for example, pair) that would interact by themselves and with the resident three quarks {u, u, d} as shown in Figure 2. The result of the QQD interaction, , can be collectively rounded up into dual―the primary and the echo―forces, that is,

, (25)

where, with,

,

and

.

The primary interaction alone strengthen the basic interaction strength

by the factor of

possibly strengthening the residual QQD force up to the maximum of. The Equation (25)

thus provides a pronounced (virtual) strengthening of the strong interaction force in the nucleon, providing a simple yet definitive QQD physics for the asymptotic freedom without the arduous QCD that blatantly violates the Einstein’s 1951 criterion to the extreme.

The expectedly complicate interaction scheme here is not yet determined. The excited (3/2) baryon decuplet states (see §12) as compared with the octet (1/2) states (see §11), for example, indicates that the perturbational quark pair (pion) may be produced in the outer domain of the nucleon, and the asymptotic freedom pressure increase could further compress the three residual quarks to cause some mass increases, while the quark pair themselves may contribute the mass near

with the QQD gluon force of F_pion ≈ 20.25, in close agreement with the observed meson mass of 144 MeV.

This may enable the pion to leak out to the nucleon interspace and generate the gluon generated binding force between nucleons in

The power of virtual interaction contingencies, for example, exhibited by the virtual W boson (of huge 80 GeV mass) production in the beta decay, is amazing. The mysterious asymptotic freedom now being proven to be the influence of the simple (virtual) quark-antiquark pair (meson) production, the cryptic penta-quark state as well as the “gluon ball”, for example, can now be plainly explicable by QQD. Most importantly, by establishing the QQD in parallel to QED, the strong interaction can now be studied by the ab initio approach nuclear physics that incorporate the spin-orbit coupling contribution.

The subject of nuclear biding is important in the development of the observed Universe. But, neither Yukawa, nor the adherents to his physics, ever bothered to explain the actual mechanism of pion exchange and how the process could generate the nucleon binding force. Moreover, it has now been shown that it’s the gluon―not the offhand pion exchange―that generate the strong binding force. This important, yet eschewed subject deserves a QQD analysis in a separate paper.

11. Baryon Octet (1/2) Ground States

The spin dispositions in the baryons reveal certain characteristic traits, and the QCD expected the proton {uud} spin to be determined by one of the u-quark, the remaining u and d quark spins adding to s_u + s_d = 0 as shown in the Figure 3(a). The experimental observation disagrees [24] ; the proton spin comes from the d-quark, the rest adding to s_u + s_u = 0 as shown in Figure 3(b).

This is not surprising; the spare u-quark in Figure 3(a) can be disposed to tangentially quantum entangle parallel to the u-quark interned in the spin sum of s_u + s_d = 0, i.e. in s_u + s_u = 1. If the quarks interact in the orbital S-state―the Pauli’s exclusion principle can eschew the state. On the other hand, if the two u-quarks are settled a priori in the s_u + s_u = 0 in Figure 3(b); the spare d-quark cannot invoke the exclusion principle to avert the state. This indicates the decisive role of the exclusion principle in the formation of baryons.

For the barons of various combinations of three {u, d, s} quarks―all compacted by their respective QQD force compression parameters {C_u, C_d, C_s}―the masses of the following quark combination states can be predicted by Equation (24) with M(s, l) = 0.

1) All three quarks in the configuration are different. The exclusion principle is then evaded for both A and B spin configuration of Figure 3, generating the two concurrent Λ˚ (uds) and Σ˚ (uds) states. This again indicates the important role of the exclusion principle in the formation of the baryons.

2) Of the three quarks {q₁, q₂, q₃), two quarks are identical, while the 3^rd quark is different, i.e. q₁ = q₂ ¹ q₃. The spin configuration of Figure 3(b) applies here in s₁ + s₂ = 0 (with s_n denoting the spin for the quark q_n) to evade the exclusion principle, while the q₃ becoming the spare quark to give a baryon of J^p = (1/2)⁺ in the S-states. Due to the exclusion principle, only one state is possible for each possible quark combination, predicting the {p(uud), n(udd), Σ⁻(dds), Σ⁺(uus), Ξ⁻(dss), Ξ⁰(uss)} in S wave (1/2)⁺ states.

3) With the 3 identical quarks in the S-states of spin = 1/2, the states must be rejected by the Pauli’s exclusion principle as they are crossed out in Figure 4. Certain excitations in angular momentum of these states upon collisions are required to recast them to evade the exclusion principle at the higher energy excited states (see §12). The “color charge” here proves to be spurious; it could have materialized the {p⁺⁺(uuu), n⁻(ddd), Ω⁻(sss)} states as well with different color for each quark.

12. The Excited (3/2)⁺ Baryons States

It has been shown [3] that the baryon excited states usually develop along the quark-antiquark pair production. This may cause the increase in the compression force due to the asymptotic freedom, generating mass increases. The actual mass increases from the ground states (of Figure 4) to the excited states (of Figure 5) is large enough, not only to give a room for a quark-antiquark pair (pion) mass, but also room for the mass increase due to the additional residual quark compression.

In addition, the mass increases also leave an elbow room for the angular momentum animation, possibly enabling rearrangement in spin-orbit configurations [see Equation (24)], about which Sheldon Glashow declared this contingency to be “the thorn in the side of QCD” [25] .

A) All quark spins may align themselves to 3/2, with the quark1 and 2 excited, for example, to the L₁ = 1 and L₂ = 1 orbital angular momentum in L₁ + L₂ = 0. This may generate the excited S state J^p = (3/2)⁺.

B) If both the L₂ and s₂ reverse their directions to {L₁ + L₂ = 2, s₁ + s₂ = 0}, a D-wave J^p = (3/2)⁺ state may result. This allows the quarks to circumvent the Paul’s exclusion principle―not by the quark colors―realizing the {Δ⁻(ddd)*, Δ⁺⁺(uuu)*, Ω⁻(sss)*} states in (3/2)⁺ as shown in Figure 5.

13. Proton Radius Crisis

The physics of the proton has recently encountered multitudes of crises such as the nature of its size. The measurement of proton radius by electron-proton and muon-proton interactions configurations differ by a huge gulf. The difference is more than 5 times the uncertainty in either measurement, implying the probability that this is all due to the chance is less than one in a million [26] .

The electrons and muons in the conventional theory are point particles without any substructures. However, this paper has shown that to be wrong; they have different lattice charge substructures (a single basic charge bit for the electron, and 53 compacted charge sub-component bits in the muon), and their spins are determined by complex probabilistic quantum entanglement synopses.

Thus the electron is structure-wise very different as compared with the muon, and the muons and electrons do not interact with the proton in the same way during their collisions. Thus the proton’s apparent radius must differ somewhat depending on the kind of particles impacting it. This interpretation was supported by the leading experts in the field: Ron Gilman of Rutgers University said “This would be very important” and Gerald Miller of University of Washington stated “That would be monumental, truly” [27] . The proton crises in reality provide unequivocal evidence for the validity of the particle structure in the unified theory proposed in this paper.

14. Conclusions

This paper along with the preceding papers [3] [4] and [5] has unified the four interaction modes with their distinct strengths, resolving that all interaction physics are generated from the unique source of electronic charges. Nature in terms of this Unified Theory of Everything has proven to be not only simple in essence, but also remarkably astute in the designing of the Universe, enabling for the first time to provide the straight answers to many problems that have been considered too intricate to be ever explainable. A partial list of the highlights is as follows:

1) Determination of all fundamental particle substructures and their masses in one-to-one agreement with observed data (in addition, the unified theory explains not only the dark matter and energy, but also, for example, the matter asymmetry in the observed Universe as well).

2) Physics behind the three generation formations both for the quarks and leptons.

3) General baryon mass determinations by the simple arithmetic addition of the compacted quark masses.

4) The large innate masses for the composite {Z, W} bosons and the origin of their spins that reject the Higgs physics.

5) The dual nature of W boson that explains the two different deuteron lifetimes observed.

6) The proton crises, instead being quandaries, are categorical proofs of the particle structure and unified physics.

7) The universal dispersion constants {ћ_s, ћ_em, ћ_w, ћ_g} that can help explain, for examples, the black hole as well the dark matter and energy.

8) Derivation and explanation of the long mystifying fine structure constant “137” that leads to QQD.

9) The strong interaction in terms of QQD, not in QCD.

10) The asymptotic freedom in terms of QQD, not in QCD.

There are more wake-up-call achievements to be cited. The remarkable insights cited above over the extensive purview of hard-core mysteries in the particle physics, however, are more than enough to conclude that the proposed theory is basically true and correct, enabling the long-awaited revolution in the modern particle physics. The author now invites the world for the open-minded collaboration.

Acknowledgements

The author dedicates this paper to the memory of the Physics Nobel Prize Winner, Dr. Hans Bethe, his great teacher and benevolent counselor at Cornell University. He also thanks Drs. Michael Stauber, Jerry Padawer, Milton Heonig, Michael Nauenberg and many other colleagues for their help and encouragement that the author has found indispensable.

Footnote

To avoid the excessive reiterations of the earlier purports, intimate reviews of the work in [3] - [5] are recommended.

Cite this paper

Paul Kiu S. Suh, (2015) Unified Theory of Everything and QQD. Open Access Library Journal,02,1-17. doi: 10.4236/oalib.1102000

References