Received 5 October 2015; accepted 23 October 2015; published 29 October 2015

ABSTRACT

Special Relativity Theory (SRT) is from time to time subject to critical assaults. There are several logically deduced discrepancies inherent in SRT (paradoxes) which demand a scrupulous examination. In this paper a new thought experiment, including two frames of reference is presented. Two trains are hurtling in opposite directions past one another in a symmetrical manner, but substantially asymmetrical events occur. This consideration leads to a contradiction in the notion of “relativity of simultaneity” ― the basic tenet of SRT.

Keywords:

Special Relativity Theory, Relativity of Simultaneity, Paradoxes

Subject Areas: Special Theory of Relativity

1. Introduction

The Special Relativity Theory (SRT) is from time to time subject to critical assaults. It is worth to mention a rather recent paper [1] by Ranzan who casts doubt on the first principal tenet of SRT ― independence of the speed of light on an arbitrary moving observer. Another critic is present in paper by Leus which aims the second principal tenet of SRT ― the so-called relativity of simultaneity. In the flat Minkovskian space-time the pseudo- Euclidian metric is defined by notion of the space-time interval “s” between two points, i.e. events. If s is real (time-like interval), the strict order of events is determined. If s is imagery (space-like interval), a strict order of events does not exist. This property of the Minkowskian space-time gives birth to the “triplet paradox” [2] . The present paper is intended to adduce one more paradoxical situation concerning the relativity of simultaneity that leads to irreconcilable controversy in the very heart of SRT.

It should notice an interesting attempt to cope with the curse of relativity of simultaneity due to introducing of a global space-time coordinate system: “Given the definition of a global coordinate system… the definition of global simultaneousness is trivial [3] .” The author believes that “The global coordinate system defined in Section 3.2 is compatible with SRT/GRT”. Unfortunately, concerning GRT (general relativity theory) this belief is erroneous. The dominant model of the Universe, starting from a singularity due to the big bang, precludes any global coordinate system in the closed space-time (no edges of the Universe exist) with a high curvature. So, the notion “age of Universe” is barely meaningless in the limits of this cosmological model [4] .

2. Thought Experiment with a Predictable Outcome

Two almost identical locomotives A (alighting) and B (bombing) are rushing along a double track railway in opposite directions, and they pass one by another during a small stretch of time (Figure 1). Locomotive A has two bright lamps mounted at two different levels, “up” for the front lamp and “down” for the rear one, on the outside, facing the parallel track, on which locomotive B is moving (Figure 2, left). The horizontal distance between their centres is L.

Locomotive B differs structurally from A due to small round windows, replacing the lamps, but maintaining the same levels of centres, at the “down” for the front window and “up” for the rear one (Figure 2, right). The

horizontal distance between their centres is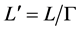, where relativistic gamma-factor, v is

locomotive A relative to locomotive B, and c ― speed of light. These windows, facing the correspondent lamps speed of the (whilst passing of locomotives one near another) are the inputs to two identical guide-tubes, conducting light from the correspondent lamp into central compartment of the second locomotive (Figure 3).

At the centre of the locomotive B is situated an exploding device with a special controller operating a detonating fuse. This controller is represent by an optoelectronic apparatus, working according to binary logic. It implements the well-known function of logical multiplication-the double input operation 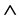(AND gate). Output signal is non-zero only if both inputs are non-zero (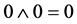, , 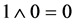,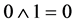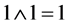). The operate time (actuation time) of the coincidence circuit must be sufficiently small to discern successive light pulses occurring from the two inputs.

In the proper reference frame 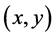of the light source the distance between its lamps is L. In the proper reference frame 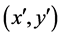of the bomb the total length of both vacuum guide-tubes is, where 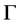is gamma-factor defined above. Let the light source is moving along the 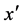-axis at speed v relative to the stationary guide-tubes (Figure 4). In the proper reference frame of bomb the distance between lamps becomes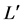, the illumination of the “up”-window and illumination of the “down” window are simultaneous events, therefore light signals starts in both guide-tubes at the same moment. Due to an obvious symmetry the optoelectronic controller

receives two signals simultaneously, and engages the exploding device, ― the bomb blows up.

However, in its own reference frame of locomotive A symmetry is absent (Fitzgerald-Lorentz contraction!). In the reference frame of the light source (Figure 5) the guide-tubes are moving at speed, but the light has the same speed c according to the relativistic rule of addition

(1)

The length of the tubes becomes, so first the “up”-window is illuminated and later the second, “down”-window is illuminated (relativity of simultaneity!). The light passes all length of the right tube during time. The light passes all length of the left tube during time and the total time, elapsing from the moment of illumination the input of the right tube, is

. The time difference between signals, arriving to the controller, is

(2)

Let us insert explicitly the relativistic factor in the formula (2):

We obtain identical zero for the time difference, therefore both light signals come to the controller at the same time, hence the bomb does blast as viewed from the reference frame of the light source.

3. Version of the Experiment with Fiberglass Cables

Let us substitute the vacuum tubes for fiberglass cables. The speed of light in a moving medium does obey the rule (1) according to special relativity, but instead of c we have to use, where n is refractive index. The speed of light in the left cable relative to the cable itself, as viewed from reference fame, is

(3)

and for the right cable:

(4)

Substituting (3) and (4) into (2) gives:

Here also the bomb blasts as viewing from both reference frames.

4. Fresnel versus Einstein

For the speed the formula for addition of speeds v and may be transformed by mean of expansion in a power series:

Rejecting the terms of higher order, we come to the formula, where c ― light speed in vacuum, and n ― refractive index. This expression, valid for phase velocities, fully coincides with a version, which Fresnel got many years before Einstein and was verified by the Fizeau experiment [5] . In the proper reference frame of the exploding device nothing changes because both cables are stationary and due to a whole symmetry bomb blows up.

Consider the situation from the point of view light source reference frame. Here we have

So, in place of (2), we get

(5)

Let us calculate the difference

(6)

Using (6) in (5) gives

(7)

This resulting time difference in (7) is evidently more than zero. If, the time difference is negligible, but for speed v tending to the light speed it become appreciable. Hence, we should accept that from viewpoint of the A-reference frame the signals reach the optoelectronic controller in moments separated by duration of time (7). As a consequence, the coincidence circuit does not work, the detonating fuse remains untouched, and the explosion does not occur.

Transition from phase velocity to group velocity changes nothing in this paradoxical situation. In this case the group velocity of light in the moving medium according to Fresnel is

(8)

where for the range of visible light [5] . We have

(9)

Substituting (9) into expression for signal’s time difference we get

(10)

which is obvious for.

On this condition the Einstein formula for group velocity is as follows:

(11)

That is different than the Fresnel Formula (8) in this case [5] . We have

Calculation gives the following expression:

The signal’s time difference would be

(12)

For the real values of refractive index the denominator and the numerator are always positive, which is to say that sign of total expression (12) is always plus. We have, hence in the case of group velocities of light the signals come to the controller non-simultaneously and so the detonating fuse remains inactivated from the viewpoint of reference frame. The paradox persists: the bomb has blown up and the same bomb has not blown up. In other words, at least one locomotive lies in wreckage, ― and both locomotives are going safe and sound.

For the locomotive velocities that are small with respect to the velocity of light the phase velocity difference between the Fresnel and Einstein predictions is a negligible value, but for group velocity it is not a negligible value. For those, who believe that special relativity is correct at any speed, they may dismiss this comparison as not worth pursuing. Nevertheless, only “His Majesty” experiment can be a final arbiter.

The Formulae (8) and (11) lead to cardinally different results (10) and (12). Notice, the delay by Fresnel differs from that by Einstein not just with value but even has opposite sign: the left fiberglass cable turns to be more rapid than the right one, contrary to the Einstein case. This feature stems from the starting expressions for group velocity given by Fresnel (8) and Einstein (11), which validity is subject to an experimental checking suggested in [5] . Objective choice may be done between Fresnel and Einstein views with the aid of an up-to-date laboratory equipment. The setup costs several order of value less than the gigantic Large Hadron Collider ($6 bn to build and $1 bn per year to operate). Is this an excessive price for the “New Michelson-Morley” test? The worst fate is for this crucial experiment to be put on the back burner of research kitchen.

5. Conclusions

A number of paradoxes have been noticed in the realm of SRT and their solutions have been found also within the same theory. However, in the case of “bomb paradox” there does not appear to be any in the field of vision. If the truth is to be told, such a fancy trick could not be tolerated for a domain of knowledge, pretending to be treated as natural science. This “bombing attack” casts doubt on the principal tenet of the theory ― relativity of simultaneity, valid for each pair of events separated by a space-like interval. Unfortunately, locomotive speed, reaching a quarter of that of the light, is unattainable for railways in the meantime (smile!), so the opportunity of experimental checking does not present itself any time soon. That is why either real experimental testing of the relativity of simultaneity would be of great importance. Such an acceptable experiment is suggested in a paper by Wagner [5] , where light itself fulfils the function of locomotive. Wagner is able to show that the Fresnel and Einstein predictions differ when a direct comparison of laser pulse arrival times is made for moving clockwise and counter clockwise dual medium fiber optic loops.

There is something inconsequential in how Einstein treats the light in the medium: it loses the property of speed invariance. The value is obtained by an observer stationary with respect to the medium, but any otherwise moving observer does not measure the speed as. In the current year Special Relativity marks its 110-anniversary. During this time a queue of questions has accumulated, which is hankering after logical and experimental solutions on the base of new ideas, which could give a clean slate to go forward. 110 years ago Einstein had destroyed the classical idea about absolute nature of space and time… Perhaps, relative times come to their finale? Maybe, the absolute time for getting revenge is looming? Possibly, Einstein’s equations will be included in a future wider theory?

Acknowledgements

The author thanks Mr Barry Smith from the University of Liverpool for valuable help while preparing this paper.

Cite this paper

Vladimir A. Leus, (2015) On an Optical Paradox in Special Relativity. Open Access Library Journal,02,1-7. doi: 10.4236/oalib.1101963

References