Received 3 October 2015; accepted 23 October 2015; published 28 October 2015

ABSTRACT

I propose a phenomenological model for the decay of black holes near Planck mass. The decay takes place via a quantum state between general relativity and a grand unified field theory like SO(10). This group is favored also by a no-scale SUGRA GUT model for Starobinsky inflation by other authors.

Keywords:

Quantum Black Hole, Singularity, Dark Matter, Grand Unified Theory, Standard Model

Subject Areas: Particle Physics

1. Introduction

The purpose of this note is to propose a quantum model for a decaying (disappearing) black hole [1] [2] . The model is defined on the horizon of the hole. The key element is the gravon state, a critical state which connects general relativity to a grand unified quantum field theory (GUT).¹ Instead of vanishing totally after enough of Hawking radiation a black hole, with mass above the GUT scale, triggers the operators of a grand unified quantum field theory like SO(10). Thereafter the black hole energy decays into SO(10) particles and finally into standard model (SM) particles.

The SO(10) GUT gets support from a different direction, and time, in the universe. In [3] the authors study Starobinsky inflation in a renormalizable grand unified theory based on the SO(10) gauge group with no scale supergravity theory (SUGRA).

The black hole decay model is not designed to give new predictions for cosmic microwave background (CMB), or any other, measurements. Most current models, like the Starobinsky or the Higgs inflation model, compare very well with all available data. The purpose of the model is to take a new look “inside” black holes.

With the Planck scale having its the conventional value 10¹⁹ GeV finding the possible gravon particle near that mass value is hard. Gamma-ray signals from the sky may be a promising way. A gamma-ray, or jet, with energy about half the Planck mass would be a favorable signal for the model. In fact, primordial black holes (PBH) with mass about 10¹⁵ g will be evaporating today and their abundance is constrained by the flux of gamma-rays, for a comprehensive treatment see [4] . Experimental estimate of its lifetime could give information of the internal properties of a black hole. A long lifetime would indicate gravitational and/or inflationary matter properties of the internals of BHs while a short lifetime would be a sign of SM particle internals including QCD contributions.

In this note I disclose the physical motivation and description of the model. In Section 2 I discuss the core qualitatively. Section 3 is devoted to SO(10) SUGRA GUT inflation model rich multiplet structure. I finish in Section 4 with conclusions.

2. Properties of the Gravon

The universe consists of classical general relativity and a grand unified quantum field theory of particles. The gravon is a critical connecting state between these two. As seen from the quantum side there is the equivalent of state vector collapse into the classical theory. Seen from the classical side the black hole looses its horizon and makes a transition into quantum fields. The horizon obviously requires proper mathematical treatment, but the physical picture given here seems clear.

Properties of the gravon model of black holes are the following:

1) the black hole generates the gravitational field of general relativity at r > r_c, at r = r_c there is the horizon, and with r < r_c there is nothing dynamical, in particular no singularity,

2) the gravon is a critical state between a minimum energy classical black hole, with energy just above $\MP$, and a quantum field with maximum energy just below M_Planck,

3) the critical state makes a transition up in energy to a black hole by absorbing a graviton and down to a fireball by emitting a graviton². The fireball does not have a horizon and it decays explosively into SO(10) particles. Properties of black holes, other than the core, are beyond the scope of this note,

4) for calculational purposes with Feynman diagrams the fireball can be approximated by a heavy Higgs-like scalar (or a fermion). The energy scale is 2 - 3 orders of magnitude above the grand unified theory scale. SO(10) is a well proven GUT group which accommodates all one generation quarks and leptons in a 16 dimensional spinorial representation (16). Therefore at the energy considered, all particles have zero mass, all interactions have the same strength, all gauge bosons 45 can be produced freely and all quarks can transform into leptons. The Higgs come in the representations 10, 16 and 45. Gravity is not, for the present, part of unification,

5) the gravon is a horizonless remnant of a thermally end-radiated black hole, either stable or with some (short I suppose) lifetime [6] . Remnants have no singularity or information loss problems, see the recent review [7] .

Quantization of GR, outside black hole horizon, is not part of this scheme but it can be done independently.

3. SO(10) in Inflation

In [3] the authors study inflation in a renormalizable grand unified theory based on the SO(10) gauge group with no scale SUGRA. The authors show that a renormalizable Wess-Zumino superpotential of SO(10) GUT along with no-scale Kähler potential can give Starobinsky kind of inflationary potential with specific choice of superpotential parameters. The Higgs supermultiplets the authors consider are 10, 210, 126 (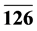). Among these, the 210 and 126 () are responsible for breaking of SO(10) symmetry down to minimal supersymmetric standard model (MSSM). The 210 supermultiplet alone can give different intermediate symmetries [8] depending upon which of its MSSM singlet field takes a vacuum expectation value (vev). Then 126 (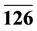) breaks this intermediate symmetry to MSSM. Successful inflationary potential can be achieved in the case of

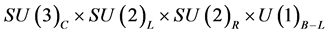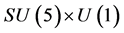, and flipped 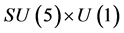symmetry.

At the end of inflation, the reheating can occur via non perturbative decay of inflaton to bosons of the intermediate scale model. After the end of reheating, when universe cools down, the finite temperature potential can have a minimum which corresponds to MSSM and the universe rolls down to this minimum at temperature << T_R (reheat temperature).

In this note the interest is in the multiplet structure of the inflation model. The minimal supersymmetric grand unified theory based on SO(10) gauge group has 10 (H_i), 210 (Φ_ijkl) and 126 (Σ_ijklm) (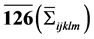) Higgs supermultiplets. The representations H_i is 1 index real, Σ_ijklm is complex (5 index, totally-antisymmetric, self dual) and Φ_ijkl is 4 index totally-antisymmetric tensor. Here 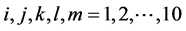run over the vector representation of SO(10). The renormalizable superpotential for the above mentioned fields is given by

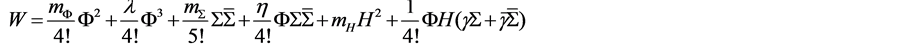(1)

The no-scale form of Kähler potential is taken to be

(2)

Here T is the single modulus field arising due to string compactification and M_Planck = 1.

The 10 and 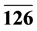are required for Yukawa terms to give masses to the fermions while 126 (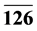) breaks the SO(10) gauge symmetry to MSSM together with 210. However to have a intermediate symmetry rather than MSSM, the 210 Higgs is sufficient. It can lead to various possible intermediate symmetries depending on which components of the 210 take vevs. The decomposition of Higgs supermultiplets required for SO(10) symmetry

breaking in terms of Pati-Salam gauge group 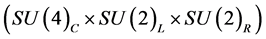is given by

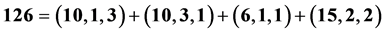
The field components which will not break the MSSM symmetry are allowed to take vevs. In this case they are [9]

The Superpotential in terms of these vevs is

The vanishing of D-terms gives the condition [9] . The symmetry breaking path of SO(10) is

where the first step is caused by 210 and the second by 126. For the first step symmetry breaking one can set. Then the possible intermediate symmetries with 210 only are [9]

1) If and, it gives symmetry.

2) If and, this results in symmetry.

3) If and, it gives symmetry.

4) If, this has symmetry.

5) If, symmetry but with flipped assignments for particles.

The superpotential in terms of vevs of 210 is given by

Here. Similarly no-scale Kähler potential is

The F-term potential has the following form

(3)

where

The kinetic term is given as. Here i runs over different fields T, p, a and ω. is the inverse of Kähler metric. After simplifying, the potential given above has the following form

(4)

The authors assume that the non-perturbative Planck scale dynamics fixes the values of. After fixing the vev for T the kinetic terms of T can be neglected. The authors study all possible cases of intermediate symmetries mentioned earlier for inflationary conditions in SO(10) with no-scale SUGRA. For simplicity they assume the fields to be real.

4. Conclusions

The present note contains a proposal of a model for black hole decay. The structure and behavior of Planck mass black holes have not, to my best knowledge, been discussed in terms of GUT fields [2] in the literature. So the present model fulfills this gap. It takes a step beyond the standard model of particles towards a GUT model of Planck scale phenomena including gravity.

The major conclusion is that the GUT theory based on SO(10) provides very much what is wanted for a description of the universe from big bang to collapse of matter into black holes, whose decays generate bouncing phenomena on all length scales. The dynamical details of the simple black hole decay model and the more involved supersymmetric inflationary theory referred to above should be studied and fitted together.

It seems one can handle the whole life cycle of particles in the (bouncing) universe using the SO(10) based GUTs. Finally, it seems that there are several elements of quantum gravity available to us if we only could see them properly organized.

Cite this paper

Risto Raitio, (2015) The Decay of a Black Hole in a GUT Model. Open Access Library Journal,02,1-4. doi: 10.4236/oalib.1102031

References

NOTES

¹This is better discussed in terms of quantum cosmology where there are transitions in the mathematical sense between different quantum universes and their collapses into classical states and vice versa.

²This reminds me of the “one-graviton” level interaction in [5] proposed to explain a wholly different process of collapse of the quantum state vector.