Received 20 September 2015; accepted 24 October 2015; published 28 October 2015

ABSTRACT

Extending the general linear model to the linear mixed model takes into account the within-sub- ject correlation between observations with introduction of random effects. Fixed covariance structures of random error and random effect are assumed in linear mixed models. However, a po- tential risk of model selection still exists. That is, if the specified structure is not appropriate to real data, we cannot make correct statistical inferences. Joint modelling method removes all specifications about covariance structures and comes over the above risk. It simply models covariance structures just like modelling the mean structures in the general linear model. Our conclusions include: a) The estimators of fixed effects parameters are similar, that is, the expected mean values of response variables are similar. b) The standard deviations from different models are obviously different, which indicates that the width of confidence interval is evidently different. c) Through comparing the AIC or BIC value, we conclude that the data-driven mean-covariance regression model can fit data much better and result in more precise and reliable statistical inferences.

Keywords:

Linear Mixed Models, Correlated Random Effects, Mean-Covariance Modeling, Longitudinal Data

Subject Areas: Mathematical Statistics, Statistics

1. Introduction

After the within subject correlation is taken into account in general linear models, the random errors are not assumed independent. Linear mixed models are setting up to solve this problems. Previous literature work on linear models and linear mixed models has mainly focused on setting up a list of possible covariance matrix structures of random errors and random effects. However, a potential vital risk still exists. If no one structure in list can fit data properly, even the best one in that list may distort statistical inference. Misspecification of covariance structures can lead to a great loss of efficiency of the parameter estimates (Wang and Carey, 2003, [1] ).

Joint modelling (Pourahmadi, (1999), [2] ) is a data-driven methodology for modelling the variance-covariance matrix similar to the general linear model framework for mean modelling. The main idea of joint modelling is considering mean and variance components in equally important level, modelling the mean, variance and correlation of response variables in three submodels, building three design matrices for mean, variance and correlation respectively, and estimating three parameters vectors for these three submodels simultaneously. The advantage of these method is to reduce the high dimensionality of computation for the covariance matrix. Modified Cholesky decomposition of the inverse of covariance matrix, , guarantees that and must be positive definite. The resulting parameters estimates are obtained and compared to those obtained using the above approaches. Assumed structures and joint modelling are compared and discussed further in terms of their ability to accurately estimate both regression coefficients and variance components.

In this paper, we aim to model covariance structures of random errors in the linear models in Section 2, model covariance structures of random errors and random effects in linear mixed models in Section 3 and model mean and covariance simultaneously based on modified Cholesky decomposition (Pourahmadi, (2000), [3] ) in Section 4. Cattle data published by Kenward in 1987 [4] were analyzed using the above three models in Section 5. The core conclusion is that real data analysis confirms the superiority of joint modelling of mean-covariance. Further discussions are followed in Section 6.

2. General Linear Models with Correlated Errors

The linear regression model assumes that the response variables and the explanatory variables are related through

(1)

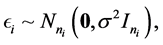
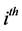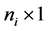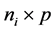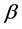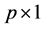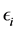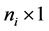where, for the subject of of m subjects, is an responses, X_i is an design matrix, is a fixed effect, random error is an random vector and assumed as normal distributed with mean zero and covariance matrix identity structure, 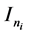is an identity matrix. Under Gauss assumption, ,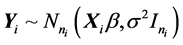

However, response in real data may be not independent. The inferences of the regression parameters of primary interest take account of the likely correlation in the data. So linear models with correlated errors is considered,

(2)

Under this assumption, , where.

2.1. Random Errors in AR(1) Covariance Structure

In this model, for the subject, the element in has the form

(3)

The correlation between a pair of measurements on the same subject decays towards zero as the time separation between the measurements increases. The rate of decay is faster for larger values of. Note that if the observation times, , are equally spaced, say for all j, then Equation (3) is expressible as

(4)

where is the correlation between successive observations on the same subject.

A justification of (4) is to represent the random variables as

(5)

with

(6)

and are mutually independent random variables, to give as required. In view of (5) and (6), the exponential correlation model is sometimes called the first order auto- regressive model, because (6) is the standard definition of a discrete-time first-order autoregressive process. By substituting into (6), we obtain the conditional distribution of, given the preceding response, , as

(7)

This form treats both the explanatory variables and prior response as explicit predictors of the current outcome. So we can get the analytical form of:

(8)

2.2. Log Likelihood

The log of the likelihood is

(9)

for given, the maximum likelihood estimator for and is, namely,

(10)

(11)

where

2.3. AIC Criterion

AIC and BIC Criterion are defined as before:

(12)

where is the maximum likelihood, K the number of parameters to be estimated in the model, and N the sample size. High-order terms are ignored here.

3. Linear Mixed Models and Restricted Maximum Likelihood Estimation (REML)

The distributional assumption about in Model (2) may be too restrictive. For example, when data are collected over time on an individual such as in repeated measurements data, it is more likely that observed measurements have a high correlation within individual. The linear mixed model extends the general linear model by allowing a more flexible specification of the covariance matrix of. In other word, it allows for both correlation and heterogenous variances, although we still assume normality.

Laird and Ware (1982) [5] provided the following description of a linear mixed model

(13)

where, for the subject of of m subjects, is an responses, is an design matrix, is a fixed effect. is an design matrix, is a random effect, , random effects are independent between subjects. Random error is an random vector and assumed as normal distributed with mean zero and covariance matrix identity structure , is an identity matrix., random errors are independent between subjects.

The model also can be written in

(14)

(15)

(16)

(17)

where Y is an responses, X is an design matrix, is a fixed effect, Z is an design matrix, is a random effect, is an random error.

The method of restricted maximum likelihood, or REML estimation, was introduced by Patterson and Thompson (1971) [6] as a way of estimating variance components in a general linear model. The objection to the standard maximum likelihood procedure is that it produces biased estimators. In REML, the degree of freedom of fixed effects are taken into account implicitly, unlike in the ML where they are not. That is why the ML estimator are biased.

REML is an alternative maximum likelihood procedure which involves applying the ML idea to linear combinations of y. Denote and B the matrix defined by the requirements that and, where I denote the identity matrix. Finally, let.

For fixed, where is variance components parameters, defined as in Section 2, the maximum likelihood estimator for is

(18)

Also, the respective pdf of Y and are

(19)

and

(20)

Furthermore, and Z and are independent, whatever the value of, as we now show.

Firstly, we prove,

since. But since, this gives

Hence as required.

Secondly, we prove

Now, substituting into this last expression gives

Also,

and

Where as in the proof that.

It follows that. Finally, in the multivariate Gaussian setting, zero covariance is equivalent to independence. It follows that the algebraic form of the (singular) multivariate Gaussian pdf

of Z, expressed in term of Y, is proportional to the ratio. To obtain the explicit form of this ratio, we use

the following standard result for the general linear mixed model that

Then, the pdf of is proportional to

(21)

where the omitted constant of proportionality is the Jacobian of the transformation from Y to. Harville

(1974) [7] shows that the Jacobian reduces to, which does not depend on any of the parameters in the

model and can therefore be ignored for making inferences about and. Note that the right hand side of (21) is independent of A, and the same result would therefore hold for any Z such that and.

The practical implication of (21) is that the REML estimator, , maximizes the log likelihood

whereas the maximum likelihood estimator, MLE, maximizes

4. Joint Mean-Covariance Model for Longitudinal Data

Response variables was assumed Gaussian distribution

4.1. Modified Cholesky Decomposition for Longitudinal Data

The subject-specific covariance matrices can be composed into

where is a lower triangular matrix with 1’s as diagonal entries and is a diagonal matrix with positive diagonal entries.

Denote

and have clear statistical interpretations:

a) are autoregressive coefficients in the autoregression models

b) are the innovation variances

where and.

4.2. Mean-Covariance Regression Model for Longitudinal Data

The unconstrained parameters, and can be modelled in terms of regression models

(22)

where, and are p-, q- and d-dimensional parameter vectors, associated with the covariates, and, respectively (Pourahmadi, 1999, [2] ).

For growth curve data, such as the cattle data which we want to analyse, the covariates may take the forms:

where the superscript “()” stands for the orthogonalization vector.

Linear mean-covariance model for growth curve data is

(23)

where, , and.

4.3. Advantages of Joint Mean-Covariance Model

First, mean-covariance regression models have compact form and clear interpretations, so that they can be understood easily.

Second, the numerical linear algebra method can reduce the high dimensional parameters in

into dimensional parameters in terms of and. This approach can decrease the computational time to a great extent.

Third, modified Cholesky decomposition of can guarantee that is positive definite.

Fourth, this model can be used commonly. For special cases, this approach can also be valid with certain constraints placed on and. For example, AR(1) structure

4.4. Maximum Likelihood Estimation for Joint Modelling

For clarity and simplicity of presentation, we only consider standard multivariate data or balanced longitudinal data (Diggle and Kenward, 1994) [8] . For, we assure that are independent -dimension vectors, where stand for the repeated measurements on the subject,. is design matrix and is vector of mean parameters. We assume that the components and of the covariance matrix, are modelled as (22), so that the likelihood function has three representations corresponding to the three submodels in (22).

Log-likelihood function is

(24)

4.5. Algorithm for Calculating Parameters

Step 1. Select an initial value for.

Step 2. Compute and its factors and to be used as initial values for T and D in the next step.

Step 3. For the inner loop, compute by solving the last two equations above using Newton-Raphson method. At convergence, compute and and form.

Step 4. Update using

Step 5. Stop the process if. Take as an estimate of and form the estimate. Otherwise, repeat Steps 2 - 4 replacing by.

5. Cattle Data Analysis

Kenward (1987) [4] reported a set of data on cattle’s growth. 60 cattle were randomly allocated into two groups, each of which would hold 30 animals. The animals were put out to pasture at the start of the grazing season, and the members of each group received one of two different treatments, A and B say, respectively. The weight (response) of each animal was then recorded 11 times to the nearest kilogram over a 133-day period. The first 10 measurements were made at two-week intervals and the final measurement was made after one-week interval.

We extract the best structure in different models from different models and put them in the Table 1. The second column gives the result for classical linear model with identical matrix of random errors in Section 2. The third column shows the result for linear model with AR(1) structure covariance matrix of random errors in linear model in Section 2. The fourth column represent the Model (13) (AR(1) structure for random effect and AR(1) structure for random error) in Section 3. The last column lists the joint modelling of mean-covariance regression in Section 4.

6. Conclusions and Discussions

The main conclusions of this paper include:

a) The estimated mean value for the response variable and the estimators of fixed effects parameters are similar whatever the covariance structure is chosen.

b) The standard deviation of fixed effects parameters estimates is relatively different, which indicates the confidence intervals depend on the specification of covariance structure.

c) As a model selection criterion, AIC or BIC value is very important. The smaller the AIC or BIC value is, the better the model is. We conclude that the joint mean-covariance regression model is the best model for analysing cattle data. Note that in all of these models, the sample size in AIC or BIC value is 660.

Apart from the above three conclusions, we can see some other hiding connotations. In the first column of Table 1, we assume all measurements are independent, and then the maximum marginal log-likelihood value is −2782.644. When extending this model and assuming some correlations in successive measurements within individual, for example, the first order autoregressive model AR(1), the result shown in the second column becomes much better. The maximum marginal log-likelihood value increase from −2782.644 to −2289.697.

Simultaneously, AIC value reduces from 5575.288 to 4591.395 and BIC from 5597.749 to 4618.348. Obviously, these two values reduce remarkably. Large reduction implies that the correlation between successive observations should not be ignored. It also implies that the joint mean-covariance model provides correct information from the increasing of log likelihood or from changes of AIC and BIC value.

What’s more, we expect that if the structure of variance is AR(2), the result will be better than AR(1) structure. This part of work can be done as further work.

When we separate the variance-covariance matrix for each animal, , into two parts, for random effect between subjects and for random error within subject. The maximum log-likelihood value increases very little (from −2289.697 to −2273.92) compared to the last increase from column 2 to column 3. If is not AR(1) structure, for example, we try identity and identity for, the log-likelihood value in the linear mixed model is not better than that in general linear model, which indicates that the AR(1) structure for is more appropriate than other specifications.

Another further work on the cattle data analysis that may be carried out is to assume that different groups of animals may have different covariance structures, unlike in this dissertation where we assume the same covariance structure applied in both groups of animals. Other modelling methods, for example, nonlinear regression model might be also used to analyse cattle data.

Acknowledgements

We thank the editors and the reviewers for their comments. This research is funded by the National Social Science Foundation No. 12CGL077, National Science Foundation granted No. 71201029, No. 71303045 and No. 11561071. This support is greatly appreciated.

Cite this paper

Yin Chen,Yu Fei,Jianxin Pan, (2015) The Effects of Covariance Structures on Modelling of Longitudinal Data. Open Access Library Journal,02,1-10. doi: 10.4236/oalib.1102086

References

NOTES

^*Corresponding author.