Open Access Library Journal
Vol.02 No.10(2015), Article ID:68728,9 pages
10.4236/oalib.1101920
A Revised Model of Photon Resulted by an Etherono-Quantonic Theory of Fields
Arghirescu Marius
State Office for Inventions and Trademarks, OSIM, Bucharest, Romania
Email: arghirescu.marius@osim.ro
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 October 2015; accepted 18 October 2015; published 23 October 2015

ABSTRACT
By an etherono-quantonic theory of the author [1] , which deduces that the magnetic field of a magnetic moment is generated by an etherono-quantonic vortex GM = GA + GB of etherons and of quantons with mass mh = h/c2, giving the magnetic induction B, a revised model of pseudoscalar photon derived from the Munera’s model and the Hunter-Wadlinger model is proposed, formed by two vectorial photons with diameter l/p, deformed to the speed direction to the value: l/2 proportional with the speed. The revised model of photon is compatible with the ondulatory and the corpuscular properties of the particles and allows a phenomenological microphysical explana- tion for the Kerr and the Cotton-Mouton effects and other similar effects. It is explained also microphysically the magnetic rotating polarization (the Faraday effect). The model indicates the variation of the quantum vacuum refraction index in the presence of a strong electric E-field or magnetic B-field.
Keywords:
Pseudo-Scalar Photon, Etherono-Quantonic Vortex, Magnetic Field, Kerr Effect, Cotton-Mouton Effect, Munera Model
Subject Areas: Theoretical Physics

1. Introduction
The dualism: wave-corpuscle of the light determined the proposal of some pseudo-scalar photon models (for a photon spin: S = h/2p) of solitonic type.
To explain the wave-particle dualism of the pseudo-scalar photon, H. A. Mùnera considers the photon as a semi-classic vortexial doublet of particle-antiparticle pair, which explains the frequency and the repose mass of a photon, [1] , considering preonic vortexes of quasi-constant density, formed in the quantum vacuum. A photon model was proposed also by Lenhert, [2] which deduced a photon diameter: d = λ0/π and which indicated a non-null rest-mass of the photon, resulted by the fact that it was associated with the photon spin and it explained the photoelectric effect and the photon’s splitting.
Geoffrey Hunter and L. P. Wadlinger [3] proposed a solitonic model of photon corresponding to the Einstein’s concept of photon considered as a localized and confined electromagnetic wave in a circular volume of an ellipsoid with the length along the propagation axe―equal to the associated wave-length, λ, and the photon diameter: df = λ0/π.
According to an etherono-quantonic theory of the author based on the galileian relativity, which sustains the possibility of particles cold genesis (CGT, [4] ), the magnetic field is generated by an etherono-quantonic vortex GM = GA + GB of s-etherons (sinergons-with mass ms » 10−60 kg) giving the magnetic potential A by an impulse density: ps(r) = (rs×c)r and of quantons (h-quanta with mass: mh = h/c2 » 7.37 ´ 10−51 kg), giving the magnetic induction B by an impulse density: pc(r) = (rcvc)r, generated by a magnetic moment of an atomic particle but also by a magnet or an electromagnet.
The known relation: B = rot×A is explained in the theory by the conclusion that the xB-field lines of the magnetic induction B having a quantum density rB(r) are materialized as quantonic vortex-tubes formed around some oriented pseudostationary quanta of the electric field (named “vectons”, i.e. vectorial photons, with mv = 3 ´ 1010mh = 2.2 ´ 10−40 kg) accumulated from the quantum vacuum by the quantonic vortex GB of the B-field, generated by the gradient of the sinergonic impulse density of the GA-vortex: ps = rs(r)×c, according to the equations:
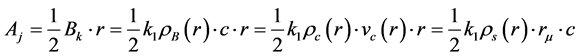 (1)
(1)
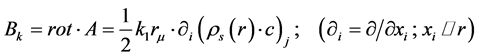 (2)
(2)
with: k1 = S0/e = 1.57 ´ 10−10 [m2/C]si, (S0 = 4pa2; a = 1.41 fm); rm―the Compton radius of the considered electric charge and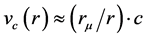 , (i.e. with rc(r) » rs(r)).
, (i.e. with rc(r) » rs(r)).
Also, the expression of the electric field results in the theory by equation:
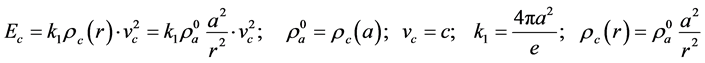 (3)
(3)
with: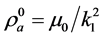 .
.
The gauge constant k1 results in the theory from a Q(M)-charge model given by a spheric-symmetric distribution of charge’s quanta: n×mc(rc) around the particle having the electron radius: ra = a, i.e.: , which generates a pressure force over the semi-surface
, which generates a pressure force over the semi-surface 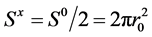 of a pseudocharge qs(m0) approximated as equal with its scattering cross section:
of a pseudocharge qs(m0) approximated as equal with its scattering cross section: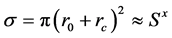 , given by the impulse density variation:
, given by the impulse density variation:
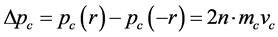 :
:
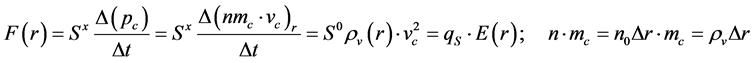 (4)
(4)
the expression of k1 resulting by the equation of equality between the electrostatic energy and the vectorial photons kinetic energy at the electron’s surface, i.e.:
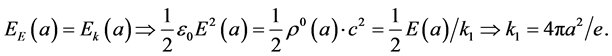 (5)
(5)
The Lorentz force results according to the theory, in the form:
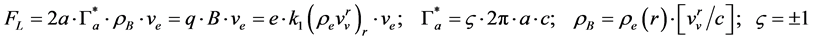 (6)
(6)
as force of Magnus type over an e-charge with the surface circulation ; (
; (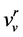 ―the relative speed of quantons forming the GB-vortex in report with the vectons of the E-field; rB―the density of xB-vortex-tubes considered with the vorticity speed: w×r = c).
―the relative speed of quantons forming the GB-vortex in report with the vectons of the E-field; rB―the density of xB-vortex-tubes considered with the vorticity speed: w×r = c).
Also, the theory deduces the variation of the Compton radius, rl and of the fermion’s magnetic moment m = e×c×rl/2, inverse proportional with the density in which is placed the particle’s superdense kernel, (the particle’s centroid): (rl; m) ~  as explanation of the dependence: mp ~ (mp)−1.
as explanation of the dependence: mp ~ (mp)−1.
The theory retrieves the Munera’s conclusion regarding a composed model of pseudoscalar photon formed as doublet of vectorial photons with spinorial mass (named “vexons” in the theory) and sustains also the possibility of a cold genesis of particles, which results theoretically in a chiral soliton model as Bose-Einstein condensate of photons in the electron’s case and of “gammons” (pairs of degenerate electrons, i.e. of quasielectrons: gc = (e+ − e−)) in the nucleon’s case.
2. A Revised Model of Photon
It may be observed that if the Múnera’s model of photons is dimensioned like in the Hunter-Wadlinger model, considering the simple photon as a doublet of two vectorial photons with mutually anti-parallel spins S = ħ/2 and a mean diameter: dw = λ/p and considering the hard-gamma quanta as a doublet: negatron-positron, gc = (e+ − e−), with opposed spins and the energy: εγ = hn = 2mec2, it results that the electron of a gc-doublet may be assimilated with a vectorial (semi) photon, 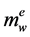 , with a rl-radius which results 1/2 from the Compton radius of a free electron: rl = λv/2p, (λv = 2λ), i.e. a degenerate electron Compton radius,
, with a rl-radius which results 1/2 from the Compton radius of a free electron: rl = λv/2p, (λv = 2λ), i.e. a degenerate electron Compton radius, 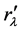 , possibility conform to the dependence
, possibility conform to the dependence
Because that according to CGT, the magnetic field B is given by a vortex of sinergons and of quantons which has the rotation speed: w×r = c inside the pseudo-cylindical volume of rl:
between 

gy of a spinorial GS vortex of quantons, which do not contribute to the inertial mass mv(w) of the photon core, it results for the proposed revised model of photon, the equation:

In this case, it results that:
This equality: ms = mw is argued in CGT by the fact that for a vectorial photon with the rw―density variation with r-1―for a pseudo-cylindrical ul―volume or with r-2―for a spherical ul―volume, the vectorial photon spin results of value:

so-equal with the value considered for fermions by the quantum mechanics.
The explaining of this equality: ms = mw, may be given by the chiral sub-solitons forming condition [5] which specifies that the energy EG = mGc2 = 2Em of the mass-generating chiral soliton field, given in this case by the sinergono-quantonic vortex
However, the explaining of the wave-particle dualism of the photon in only partially solved in this stage, because that the photon length must be: ln = l, so-greather than 2dw = 2l/p.
The problem may be solved by the conclusion that the vectorial photon volume ul is a little expanded over the value dw to at least one direction. We have in this sense three theoretical possibilities:
a) the collinear orientation of the vectorial photons; this case correspond to the Hunter-Wadlinger photon model, but it gives a longer vectorial photon, longitudinally polarised, which not explain causally the ondulatory properties of the photon, given by: H ^ c;
b) the vexon volume expansion along axis x, y ^ c; this possibility suppose that the vortexial energy Em of vec-
torial photon is contained by a volume: 
radius of the vectorial photons, of value:
c) the vexon volume expansion along the axe x // vp ≤ c; this possibility suppose that the vortexial energy Em of vectorial photon is contained by an ellipsoidic volume with the length : lw = l/2, i.e.:



relation which results in the hypothesis of a relativist etherono-quantonic impulse density: pr = rrvp given by the equation:

in which: kv―proportionality constant; nk―the kinematic viscosity of quantum vacuum. The considered ansatz (10) will be justified afterward.
By Equations (9), (10), the revised model of photon may explain also the photon wavelength variation with the photon’s speed in an optical medium with a specific index of refraction, n, i.e.:

in the form:

in which 
For: lw/2 » l0/p, (vv ≤ 0.64c), the dynamic equilibrium for the vortexed quantons or clusters of quantons inside the Compton radius: rl = l0/2p, is given by a magneto-gravitic force of Magnus type generated by the sinergonic vortex over the quantons rotated with v = c to the vortex line: lr = 2pr, in the form:

by the resulted condition:


Also, because that in the case of light propagation in an optical medium in the presence of an intense electric E-field or magnetic B-field, the etherono-quantonic density rr of the quantum vacuum is supplemented with a value: Drr ~ eE2 or 

We observe that the solution c), conformed with the Figure 1, by the resulted dependence:

Also, by the model, it results that a pair: photon-photon or photon-antiphoton, formed as two identical photons weakly coupled in phase or antiphase, may be splitted into two photons which thereafter may interfere, in accordance with the double slit experiment result, (the vexonic inertial mass of each photon cross the slit carrying its electromagnetic vortex).
3. The Kerr and Cotton-Mouton Effects Explaining
Because that in the case of light propagation in an optical medium in the presence of an intense electric E-field
Figure 1. Revised model of multi-photon, (lp = 1.5l).
of magnetic B-field, the etherono-quantonic density rr of the quantum vacuum is supplemented with a value: Drr ~ eE2 or 

(h = rrnk; nk―kinematic viscosity of quantum vaquum), acting over the mp inertial mass of photon and giving a deceleration of mean value ae, in the form:

The refraction index results from Equation (15) in the form:

We observe that if Kn quasi-constant, because that in CGT is considered a radius: rw » kra = (0.4 − 1)×a with a = 1.41 fm, for the inertial mass of the photons, (kr = 0.41 for vectons-equation (3) and kr » 0.7 for light photons), it results that:

So, by the prevous theoretical assumption, it is justified the ansatz (10) looking the dependence: lw(vv) ~ vv. Also, for vv it results that:

If: 


where KE and KH are the Kerr and the Cotton-Mouton constants of the optical medium.
We obtain in this case, a phenomenological microphysical explanation for the Kerr and the Cotton-Mouton effects, by a solitonic model of photon, compatible with the ondulatory and the corpuscular properties of the particles. The decomposing of a monochomatic polarised light beam in two waves: ordinary and extraordinary waves in a strong magnetic field, may be also explained by the revised model of photon, considering also the difference of the magnetic interaction with the external B-field of the two vectorial photons which gives the light photon.
Also, in the inverse Cotton-Mouton effect, when an oscillating field passes through a dielectric medium in such a way that it’s oscillations are similar to the polarization induced by the C-M effect, then a static magnetic field is created perpendicular to the direction of propagation of light. This effect is also explained by the revised model of photon, by the fact that the Gm-vortexes of light quantum vexons induces parallely oriented vortexes of a H-field in the quantum medium of the dielectric body.
It results also-from the model, that the photon may be considered un-deformed until a speed:

The refraction angle may be also explained by a model of double multiphoton (two multiphoton rows coupled in phase) which may explain also the photon’s splitting at its passing through a double slit.
If the dielectric body has a speed 



(i.e. the invariance of
The possibility: 
inside the dielectric body, by atomic vortexes, phenomenon which may explain the fact that―when the photon get out from the optical body, it regains its normal speed,
Also, the possibility to “freeze” light inside a crystal [9] may be explained by the revised vortexial model of photon, by the hypothesis of ring multi-photons forming in the magnetic field of the electrons or/and of the atoms.
We observe also that considering a speed: vv = c/n also for the vectorial photons in an optical body, the Equation (4) becomes:


i.e. is re-obtained a known relation, verified for very low frequencies of the photons, i.e. for the far-IR domain; (for higher frequencies: er = er(n)).
Also, if
The first case 
The fact that the Kerr and Cotton-Mouton effect generates a bi-refringence of the optical crystal, the fact that the Kerr effect is established with a delay of few seconds in solids and polar viscous liquids and the fact that it is known also a mechanical or a dynamic birefringence or generated by quenching, indicates that the bi-refrin- gence is generated by the atomo-molecular arrangement (orientation) which generates an anisotropy of the mean quantum 
According to the revised model of photon, the photon’s polarization plane is formed by the spins and the magnetic moments of the coupled vectorial photons which gives the pseudoscalar photon.
The scalar quantum corresponds to a couple of two pseudoscalar photons coupled in antiphase. In this case, the electromagnetic effect of Gm-vortexes of vexons is reciprocally canceled but the scalar quantum has an impulse: 
It is argued in CGT that a scalar quantum may be emitted by charges vibrated by energetic shocks.
In relation to these previous conclusions, the general microphysical way in which was deduced the Equation (19) indicates the possibility to modify the refraction index of the quantum vacuum (normally: n0 = 1) by the presence of a local intense electric E-field or magnetic B-field, according to the model. We observe also that the dependences: n~ rr and 
Also, the magnetic rotating polarization (the Faraday effect) (Figure 2), consisting in the rotation of the polarization plane of a light beam in a magnetic field parallel with its speed: H//c, with an angle:

(rv = rv(l)―the Verdet constant, the rotation sense depending on the H-field sense), may be explained by the proposed revised model of photon in connection with the quantum vortexial nature of the magnetic field considered in the etherono-quantonic theory [4] , by the conclusion that the etherono-quantonic dynamic pressure: Pd = 1/2rBc2 of the xB vortex-tubes of the magnetic induction B = rot×A, which generates the magnetic field lines, action over the inertial mw and the spinorial mS » mw mass of the vectorial photons (which gives the pseudo- scalar photon: hn = mpc2) by a pseudo-electric field Eq tangent to the xB vortex-tube, forming the B-field lines, i.e.:

according to Equations (1)-(3). So, Eq generates a rotation of the photon’s polarization plane with w depending on the sense of the xB vortex-tubes and on their density: rB ~ B, with an angle:

Similarly may be explained also the Einstein-de Haas effect, determining the rotation of a ferromagnetic bar introduced in a magnetic B-field, [4] .
4. The Gamma Quanta
In the case of gamma quanta, the phenomenon of pairs conversion: g ® e+ + e−, indicates the existence of two types of gamma quanta: soft gamma quanta, with normal ondulatory (electromagnetic) properties, which are composed according to the revised model of photon (Figure 1) and hard-gamma quanta, with altered electromagnetic properties, i.e. acting mainly by the energy of the inertial mass and composed from a partially degenerate pair: negatron-positron with the inertial mass in a volume with radius equal with the electron’s Compton radius, 

At very low temperature, T ® 0 K, when

Figure 2. The Faraday effect (the vorticity of the xB― field line determines the rotation of the photon’s polarization).
where:



It is possible to estimate empirically the expression of kd by CGT [4] , with the case of a proton formed as B-E condensate of n = 1052 gammons, (degenerate hard-gamma quanta), the mean radius h of the electron decreasing from he = 0.965 fm (of the free electron) to hn = 0.849 fm for the quasielectron of the protonic B-E condensate, according to CGT, value which is very close to the experimentally determined root-mean-square radius of proton’s charge density variation: 

with
Also, because that-according to CGT, the degenerate electrons of the protonic B-E cluster are quasi-electrons, with the charge e* = (2/3)×e characteristic to quarks, by the specific dependence: e ~ rc(a), to the rc(r)-density variation of the quasi-electron’s magnetic moment vortex, Gm, it corresponds a mean radius of the Gm-vortex: hm = 0.755 fm, [4] .
Supposing for he, hm an inverse proportionality with the quanta density in which is positioned the electronic centroid and with the distance between the electronic centroids, 

with: n―the number of bosons which forms the B-E condensate and l―the mean inter distance between the super dense electronic kernels (centroids).
Because that all superdense electronic centroids of the protonic B-E cluster are inside of the impenetrable quantum volume of the proton: ui(ri) and forms the superdense kernel of protonic Compton radius, rlp, we may approximate that: 


The difference between gm and ge suggests the existence of a proportion 
An important consequence of the empiric expression (28) of kd is the conclusion that when a quasi-electron e* which gives the u-quark’s charge inside the impenetrable quantum volume of the proton, ui(ri), is moved in the strong interaction quantum volume
that kd decreases to the value:

which corresponds to:
In the same time, this possibility resulted by Equation (28) explains the difficulty to find quarks in the free state, according to the theory.
For separate fermions, (d1-2 ³ re), kd » 1, according also to the superposition principle.
5. Conclusions
By the previous theoretical explanations of the wave-corpuscle dualism of the photon, based to an etherono- quantonic theory of fields considering a vortexial quantum nature of the magnetic field, the revised vortexial model of pseudo-scalar photon derived from the Munera’s model and the Hunter-Wadlinger model explains the ondulatory phenomena of photons by the spinorial, vortexial mass, ms of the component vectorial photons coupled with antiparallel magnetic moments, the corpuscular properties of the photons being explained by an inertial mass of the vectorial photons, mw, equal with the spinorial mass. The model allows phenomenological microphysical explanations for the photon’s wave-length variation with the value of the refraction index of the optical body and the Kerr and Cotton-Mouton effects. It is explained also microphysically the magnetic rotating polarization (the Faraday effect). The model indicates the variation of the quantum vacuum refraction index in the presence of a strong electric E-field or magnetic B-field.
The conclusion regarding the equality between the inertial and the spinorial mass of the vectorial photon and the conclusion that its spinorial mass does not contribute to its inertial mass is based to the next assumptions:
The inertial mass is given by chiral sub-solitons of high density, (“vectons” in CGT) formed and confined by the quantonic vortex Gm = GA + GH and not vanish if the Gm vortex is not vanished (i.e. the photon has also inertial rest-mass);
A quantum contributes to the inertial mass of a particle only if it is linked by a force which transmits to the particle at least partially each exterior action over it.
For a fermion, particularly for an electron, because it may be assimilated with a semi-photon, the model may explain the wave properties given by the associated de Broglie wave, also for other particles, but we observe that the proposed model corresponds to a photon for which the phase speed is equal with the group speed. By the equality: hn = mc2, the correct form of wave-length l is the form:

Also, the possibility of double multi-photon forming as chains of antiparallely coupled vectorial photons, may explain the double slit experiment by the conclusion that the Gm-vortex of the atoms which forms the slits’ margins attracts the multiphoton rows with spatially variable force, determining the light’s diffraction and suggests that a part of the incoherent light’s energy may be emitted in the form of pairs of multiphotons coupled in antiphase, having a non-ondulatory effect of scalar wave.
Cite this paper
Arghirescu Marius, (2015) A Revised Model of Photon Resulted by an Etherono-Quantonic Theory of Fields. Open Access Library Journal,02,1-9. doi: 10.4236/oalib.1101920
References
- 1. Munera, H.A. (2002) A Semiclassical Model of the Photon Based on Objective Reality and Containing Longitudinal Field Components. In: Evans, M.W., Ed., Modern Nonlinear Optics, John Wiley & Sons Inc., Hoboken, 335-385.
- 2. Lehnert, B., et al. (2000) An Extended Electromagnetic Theory. Apeiron, 7, 53.
- 3. Hunter, G. and Wadlinger, R.L.P. (1989) Photons and Neutrinos as Electromagnetic Solitons. Physics Essays, 2, 158-172.
http://dx.doi.org/10.4006/1.3035861 - 4. Arghirescu, M. (2015) A Quasi-Unitary Pre-Quantum Theory of Particles and Fields and Some Theoretical Implications. International Journal of High Energy Physics, 2, 80-103.
- 5. Kiehn, R.M. (1987) The Falaco Effect. A Topological Soliton. Talk at 1987 Dynamics Days, Austin.
- 6. Hunter, G., Wadlinger, L.P., et al. (2002) Gravitation and Cosmology: From the Hubble Radius to the Planck Scale. Fundamental Theories of Physics, 126, 157-166.
- 7. Weinberger, P. (2008) John Kerrr and His Effect Found in 1877 and 1878. Philosophical Magazine Letters, 88, 897-907.
http://dx.doi.org/10.1080/09500830802526604 - 8. Cotton, A. and Mouton, H. (1905) Comptes Rendus Hebdomadaires des Séances de l’Académie des Sciences Paris, 141, 317-349.
- 9. Heinze, G., Hubrich, C. and Halfmann, T. (2013) Stopped Light and Image Storage by Electromagnetically Induced Transparency up to the Regime of One Minute. Physical Review Letters, 111, Article ID: 038103.
http://dx.doi.org/10.1103/physrevlett.111.033601 - 10. Pohl, R., Antognini, A., Nez, F., Amaro, F.D., et al. (2010) The Size of the Proton. Nature, 466, 213-216.
http://dx.doi.org/10.1038/nature09250



