Open Access Library Journal
Vol.02 No.10(2015), Article ID:68720,14 pages
10.4236/oalib.1101836
On the Origin of Electric Charge
Johannes Antonie Josephus van Leunen
Retired Physicist
Email: hans.van.leunen@planet.nl
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 26 September 2015; accepted 17 October 2015; published 22 October 2015

ABSTRACT
By starting from a quaternionic separable Hilbert space as a base model, the paper uses the capabilities and the restrictions of this model in order to investigate the origins of the electric charge and the electric fields. Also, other discrete properties such as color charge and spin are considered. The paper exploits all known aspects of the quaternionic number system and it uses quaternionic differential calculus rather than Maxwell based differential calculus. The paper presents fields as mostly continuous quaternionic functions. The electric field is compared with another basic field that acts as a background embedding continuum. The behavior of photons is used in order to investigate the long range behavior of these fields. The paper produces an algorithm that calculates the electric charge of elementary particles from the symmetry properties of their local parameter spaces. The paper also shows that the usual interpretation of a photon as an electric wave is not correct.
Keywords:
Quantum Physics, Mathematical Model, Electric Charge, Electric Field, Embedding Field, Photon, Wave Equation, Quaternionic Hilbert Space, Quaternionic Differential Calculus, Symmetry Flavor
Subject Areas: Quantum Mechanics, Theoretical Physics

1. Introduction
Indications suggest that electrical charges are properties of space. The major indication is the fact that quaternionic number systems exist in several versions that differ in their symmetry properties. These symmetry properties are related to the way that these versions are ordered.
As a consequence, it makes sense to introduce the notion of types of spaces where each type has its own symmetry flavor. An important category of these spaces are symmetry centers. Symmetry centers float on a covering background space that has its own symmetry flavor.
Within a separable Hilbert space, such types of spaces can coexist as eigenspaces of corresponding types of quaternionic operators. That is why we will use an infinite dimensional separable quaternionic Hilbert space ℌ as our base model.
Each infinite dimensional separable quaternionic Hilbert space owns a companion Gelfand triple ℋ, which is a non-separable Hilbert space. In the separable Hilbert space ℌ the eigenspaces of operators are countable. In the Gelfand triple ℋ the eigenspaces of operators can be continuums.
In the separable quaternionic Hilbert space we introduce the concept of well-ordered normal operators. A well-ordered normal operator offers eigenvalues that have unique real parts. The eigenvalues can then be ordered with respect to the values of their real parts. We will define a well-ordered reference operator ℛ whose eigenspace acts as a model-wide parameter space. The well-ordered reference operator that provides the countable parameter space in the separable Hilbert space ℌ owns a companion reference operator ℜ in the Gelfand triple ℋ that provides a continuum eigenspace.
Fields will appear as continuum eigenspaces of normal operators that reside in the Gelfand triple. We will show that fields can be defined as quaternionic functions that use the eigenspace of the reference operator ℜ as their parameter space.
Symmetry centers reside in the separable Hilbert space and are maintained in finite dimensional subspaces. Symmetry centers exist in a small number of types that differ in the corresponding symmetry flavor. Corresponding normal operators  map these subspaces onto themselves. Superscript
map these subspaces onto themselves. Superscript 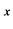 refers to the type dependent properties of the symmetry center. The center location of the symmetry center corresponds to the value of a quaternionic mapping function of its quaternionic location in the parameter space that is defined via the well- ordered reference operator ℛ and its companion ℜ. That value is a location in a background continuum ℭ. ℜ is the parameter space of the quaternionic function ℭ(q) that defines continuum ℭ.
refers to the type dependent properties of the symmetry center. The center location of the symmetry center corresponds to the value of a quaternionic mapping function of its quaternionic location in the parameter space that is defined via the well- ordered reference operator ℛ and its companion ℜ. That value is a location in a background continuum ℭ. ℜ is the parameter space of the quaternionic function ℭ(q) that defines continuum ℭ.
2. Quaternions
Quaternions can be interpreted as combinations of a real scalar and a three dimensional real vector [1] . The vector forms the imaginary part of the quaternion. The combination supports numeric arithmetic. The vector part introduces a non-commutative multiplication.
We will indicate the real part of quaternion a by subscripted 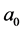 and the vector part will be put in bold font face
and the vector part will be put in bold font face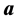 .
.
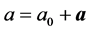 (1)
(1)
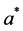 is the quaternionic conjugate of a.
is the quaternionic conjugate of a.
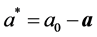 (2)
(2)
The sum of two quaternions is defined by:
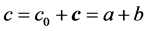 (3)
(3)
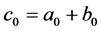 (4)
(4)
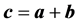 (5)
(5)
The product rule is defined by:
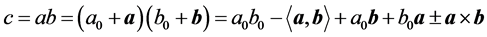 (6)
(6)
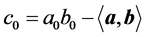 (7)
(7)
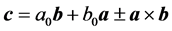 (8)
(8)
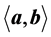 is the inner vector product.
is the inner vector product. 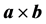 is the outer vector product.
is the outer vector product.
The 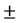 sign signalizes the choice between a right handed and a left handed external vector product. This choice indicates that quaternionic number systems exist in multiple versions. Due to the four dimensions of quaternions will quaternionic number system exist in sixteen different symmetry flavors. The handedness depends on the symmetry flavor.
sign signalizes the choice between a right handed and a left handed external vector product. This choice indicates that quaternionic number systems exist in multiple versions. Due to the four dimensions of quaternions will quaternionic number system exist in sixteen different symmetry flavors. The handedness depends on the symmetry flavor.
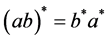 (9)
(9)
The norm of a quaternion is defined by:

The norm of a quaternionic function is defined by:

3. Quaternionic Hilbert Spaces
Separable Hilbert spaces are linear vector spaces in which an inner product is defined. This inner product relates each pair of Hilbert vectors. The value of that inner product must be a member of a division ring. Suitable division rings are real numbers, complex numbers and quaternions. This paper uses quaternionic Hilbert spaces [2] - [4] .
Paul Dirac introduced the bra-ket notation that eases the formulation of Hilbert space habits [5] .







This paper considers Hilbert spaces as no more and no less than structured storage media for dynamic geometrical data that have an Euclidean signature. Quaternions are ideally suited for the storage of such data. Quaternionic Hilbert spaces are described in “Quaternions and quaternionic Hilbert spaces” [6] .
The operators of separable Hilbert spaces have countable eigenspaces. Each infinite dimensional separable Hilbert space owns a Gelfand triple. The Gelfand triple embeds this separable Hilbert space and offers as an extra service operators that feature continuums as eigenspaces. In the corresponding subspaces the definition of dimension loses its sense.
3.1. Tensor Products
The tensor product of two quaternionic Hilbert spaces is a real Hilbert space [7] . For that reason this model does not apply tensor products. As a consequence Fock spaces are not applied in this paper.
Instead the paper represents the whole model by a single infinite dimensional separable quaternionic Hilbert space and its companion Gelfand triple. Elementary objects and their composites will be represented by subspaces of the separable Hilbert space. Their local living spaces coexist as eigenspaces of dedicated operators.
3.2. Representing Continuums and Continuous Functions
Operators map Hilbert vectors onto other Hilbert vectors. Via the inner product the operator T may be linked to an adjoint operator


A linear quaternionic operator T, which owns an adjoint operator 



By using reverse bra-ket notation, operators that reside in the Hilbert space and correspond to continuous functions, can easily be defined by starting from an orthonormal base of vectors. In this base the vectors are normalized and are mutually orthogonal. The vectors span a subspace of the Hilbert space. This works both in separable Hilbert spaces as well as in non-separable Hilbert spaces.
Let 






Let 

f defines a new operator that is based on function
Operator f has a countable set of discrete quaternionic eigenvalues.
For this operator the reverse bra-ket notation is a shorthand for

In a non-separable Hilbert space, such as the Gelfand triple, the continuous function 

Via the continuous quaternionic function



The function 




Here we no longer enumerate the base vectors with index i. We just use the name of the parameter. If no conflict arises, then we will use the same symbol for the defining function, the defined operator and the continuum that is represented by the eigenspace.
For the shorthand of the reverse bra-ket notation of operator 


Remember that quaternionic number systems exist in several versions, thus also the operators f and 
Thus, operator 

space
Similarly, 




In general the dimension of a subspace loses its significance in the non-separable Hilbert space.
The continuums that appear as eigenspaces in the non-separable Hilbert space ℋ can be considered as quaternionic functions that also have a representation in the corresponding infinite dimensional separable Hilbert space ℌ. Both representations use a flat parameter space ℜ or ℛ that is spanned by quaternions. ℛ is spanned by rational quaternions.
The parameter space operators will be treated as reference operators. The rational quaternionic eigenvalues 


All operators that reside in the Gelfand triple and are defined via a mostly continuous quaternionic function have a representation in the separable Hilbert space.
3.3. Stochastic Operators
Stochastic operators do not get their data from a continuous quaternionic function. Instead a stochastic process delivers the eigenvalues. Again these eigenvalues are quaternions and the real parts of these quaternions can be interpreted as progression values.
Stochastic operators only act in a step-wise fashion. Their eigenspace is countable. Stochastic operators may act in a cyclic fashion.
The mechanisms that control the stochastic operator can synchronize the progression values with the model wide progression that is set by a selected reference operator.
Density Operators
The eigenspace of a stochastic operator may be characterized by a continuous density distribution. In that case the corresponding stochastic process must ensure that this continuous density distribution fits. The density distribution can be constructed afterwards or after each regeneration cycle. Constructing the density distribution involves a reordering of the imaginary parts of the produced eigenvalues. A different operator can then use the continuous density distribution in order to generate its functionality. The real parts of the eigenvalues may then reflect the reordering. The construction of the density distribution is a pure administrative action that is performed as an aftermath. The constructed density operator represents a continuous function and may reside both in the separable Hilbert space and in the Gelfand triple.
3.4. Notations
The reverse bra-ket notation enables the definition of some special operators that play a unique role in the model. We will reserve special symbols for these operators and we will also use special symbols in order to distinguish separable from non-separable Hilbert spaces.
The defining function in the reverse bra-ket notation enables the definition of operators in both the separable Hilbert space ℌ and in the Gelfand triple ℋ. Still different symbols are used for reference operators ℜ and ℛ. ℴ is a stochastic operator. ρ is the corresponding density operator.
4. Well-Ordered Reference Operators
The eigenvalues of a normal operator T that resides in a separable Hilbert space can be ordered with respect to the real part of the eigenvalues. Operator 


The property of being well-ordered is restricted to operators with countable eigenspaces. However, via the defining functions, the well-orderedness can be transferred to the corresponding operator in the Gelfand triple.
4.1. Progression Ordering
A single self-adjoint reference operator that offers an infinite set of rational eigenvalues can synchronize a category of well-ordered normal operators. We use 
The selected well-ordered normal reference operator ℛ that resides in an infinite dimensional separable quaternionic Hilbert space is used in the specification of the companion quaternionic Gelfand triple. There it corresponds to reference operator ℜ. In that way progression steps in the separable Hilbert space and flows in the companion Gelfand triple. Both reference operators will be used to provide parameter spaces.
The countable set of progression values of the Hermitian part 
4.2. Cartesian Ordering
The whole separable Hilbert space can at the same time be spanned by the eigenvectors of a reference operator whose eigenvalues are well-ordered with respect to the real parts of the eigenvalues, while the imaginary parts are ordered with respect to a Cartesian coordinate system.
For Cartesian ordering, having an origin is not necessary. In affine Cartesian ordering only the direction of the ordering is relevant. Affine Cartesian ordering exists in eight symmetry flavors.
Cartesian ordering supposes a unique orientation of the Cartesian axes.
The well-ordered reference operator ℛ is supposed to feature affine Cartesian ordering.
4.3. Spherical Ordering
Spherical ordering starts with a selected Cartesian set of coordinates. In this case the origin is at a unique center location. Spherical ordering can be done by first ordering the azimuth and after that the polar angle is ordered. Finally, the radial distance from the center can be ordered. Another procedure is to start with the polar angle, then the azimuth and finally the radius. Such, spherical orderings may create a symmetry center. Since the ordering starts with a selected Cartesian coordinate system, spherical ordering will go together with affine Cartesian ordering.
Each symmetry center is described by the eigenspaces of an anti-Hermitian operator 


5. Symmetry Flavor
Quaternions can be mapped to Cartesian coordinates along the orthonormal base vectors 1, 


Due to the four dimensions of quaternions, quaternionic number systems exist in 16 well-ordered versions 


Half of these versions are right handed and the other half are left handed. Thus the handedness is influenced by the symmetry flavor.
The superscript 
This superscriptrepresents the symmetry flavor of the indexed subject.
The reference operator 

The symmetry flavor of the symmetry center

Now the symmetry related charge follows in three steps.
1) Count the difference of the spatial part of the symmetry flavor of 
2) If the handedness changes from R to L, then switch the sign of the count.
3) Switch the sign of the result for anti-particles.
Per definition, members of coherent sets 

Also continuous functions and continuums feature a symmetry flavor. Continuous quaternionic functions 

The reference symmetry flavor 


If the continuous quaternionic function describes the density distribution of a set 


6. Symmetry Centers
Each symmetry center corresponds to a dedicated subspace of the infinite dimensional separable Hilbert space. That subspace is spanned by the eigenvectors of a corresponding symmetry center reference operator

Symmetry flavors relate to affine Cartesian ordering. Each symmetry center will own a single symmetry flavor. The symmetry flavor of the symmetry center relates to the Cartesian coordinate system that acts as start for the spherical ordering. The combination of affine Cartesian ordering and spherical ordering puts corresponding axes in parallel. Spherical ordering relates to spherical coordinates. Starting spherical ordering with the azimuth corresponds to half integer spin. The azimuth runs from 0 to π radians. Starting spherical ordering with the polar angle corresponds to integer spin. The polar angle runs from 0 to 2π radians. These selections add to the type properties of the symmetry centers.
The model suggests that symmetry centers are maintained by special mechanisms that ensure the spatial and dynamical coherence of the coupling of the symmetry center to the background space. Several types of such mechanisms exist. Each symmetry center type corresponds to a mechanism type. These mechanisms are not part of the separable Hilbert space.
Symmetry centers are resources where the coherence ensuring mechanisms can take dynamic locations that are stored in quaternionic eigenvalues of dedicated operators, in order to generate coherent location swarms that represent point-like objects. The type of the point-like object corresponds to the type of the controlling mechanism.
The basic symmetry center is independent of progression. Once created, a symmetry center persists until it is annihilated. However, during creation its ordering can be synchronized with selected progression steps. Any progression dependence that concerns a symmetry center is handled by a type dependent mechanism. The type depends on the symmetry flavor and on the spin. Further, it depends on other characteristics that will not be treated in this paper, but that will appear as properties of the point-like object that will be supported by the controlling mechanism. An example is the generation flavor of the point-like particle. In this way the same symmetry center type can support electrons, muons and tau particles. Symmetry flavor and spin can be related to ordering of the symmetry center. Generation flavor is a property of the controlling mechanism.
The mechanisms that control the usage of symmetry centers act mostly in a cyclic fashion. When compared to mechanisms that care about particles, the cycles that occur in equivalent mechanisms that care about corresponding anti-particles act in the reverse direction. As a consequence many of the properties of the anti-particles are the opposite of the properties of the corresponding particles. This holds for the sign of the symmetry related charge and it holds for the color charge, but it does not hold for the mass and for the energy of the (anti)particle.
Symmetry centers have a well-defined spatial origin. That origin floats on the eigenspace of the reference operator ℛ⓪. Symmetry centers are formed by a dedicated category of compact anti-Hermitianoperators
An infinite dimensional separable Hilbert space can house a set of subspaces that each represent such a symmetry center. Each of these subspaces then corresponds to a dedicated spherically ordered reference operator





Only the location of the center inside the eigenspace of reference operator ℛ⓪ is a progression dependent value. This value is not eigenvalue of operator
Symmetry centers feature a symmetry related charge that depends on the difference between the symmetry flavor of the symmetry center and the symmetry flavor of the reference operator ℛ⓪, which equals the symmetry flavor of the embedding continuum ℭ. The symmetry related charges raise a symmetry related field 𝔄. The symmetry related field 𝔄 influences the position of the center of the symmetry center in parameter space ℛ⓪ and indirectly it influences the position of the map of the symmetry center into the field that represents the embedding continuum ℭ. Both fields, 𝔄 and ℭ use the eigenspace of the reference operator ℜ as their parameter space.
The closed subspaces that correspond to a symmetry center have a fixed finite dimension. This dimension is the same for all types of symmetry centers. This ensures that symmetry related charges all appear in the same short list.
Synchronization via Coupling
The basic symmetry center is independent of progression. Any progression dependence that concerns a symmetry center is handled by a type dependent mechanism that controls the usage of the symmetry center. The type dependent mechanism acts in a progression dependent fashion. On certain progression steps the mechanism selects a location from the symmetry center that will be used to embed a point-like object in the background space.
The background space, is maintained by reference operator ℛ. Embedding the symmetry center into the eigenspace of this operator ensures the synchronization of the symmetry center with the background space. That is why the embedding occurs at instances that are selected from the progression values, which are offered as eigenvalues by


The embedding location represents a point-like object that resides in the symmetry center. That embedding location is mapped onto the embedding continuum, which resides as the eigenspace of operator ℭ in the Gelfand triple ℋ. This continuum is defined as a function ℭ(q) over parameter space ℜ.
The locations in the symmetry center that for the purpose of the embedding are selected, form a coherent location swarm and a hopping path that characterize the dynamic behavior of the point-like object. The embedding process deforms continuum ℭ. This embedding process is treated in more detail in [8] .
7. Central Governance
The eigenvalues of the central governance operator ℊ administer the relative locations of the symmetry centers with respect to the reference operator ℛ⓪ which resides in the separable Hilbert space ℌ and maps to the reference continuum ℜ⓪ in the Gelfand triple ℋ. A further map projects onto the embedding continuum .The central governance operator ℊ resides in the separable Hilbert space ℌ. Operator ℊ has an equivalent ℭ(ℊ) in the Gelfand triple. Function ℭ(q) maps eigenvalues of ℊ onto continuum ℭ.
The reference continuum ℜ⓪ acts as a parameter space of the function 𝔄(q) that specifies the symmetry related field 𝔄, which is eigenspace of the corresponding operator.
Each symmetry center owns a symmetry related charge, which is located at its geometric center. Each symmetry related charge owns an individual field 
The reference continuum ℜ⓪ also acts as a parameter space of the function ℭ(q) that specifies the embedding continuum , which is eigenspace of the corresponding operator ℭ.
A fundamental difference exists between field 𝔄 and field ℭ. However both fields obey the same quaternionic differential calculus. The difference originates from the artifacts that cause the discontinuities of the fields. In the symmetry related field 𝔄 these artifacts are the symmetry related charges. In the embedding continuum ℭ these artifacts are the embedding events. What happens in not too violent conditions will be described by the wave equation of the corresponding field and will be affected by the local and current conditions. Since the elementary point-like objects reside inside their individual symmetry center, the embedding continuum will also be affected by what happens to the symmetry centers.
Double differentiation of field 𝔄 shows the relation between 𝔄 and ℊ.

Function ℭ(q) maps both 𝔄 and the eigenspace of ℊ onto continuum ℭ.
Embedding Symmetry Centers
The well-ordered eigenspace of a quaternionic normal operator ℛ⓪ that resides in an infinite dimensional separable Hilbert space acts as a reference operator from which the parameter space ℜ⓪ of the embedding continuum ℭ will be derived. This parameter space resides as continuum eigenspace of a corresponding operator ℜ⓪ in the Gelfand triple. This parameter space also acts as parameter space of a symmetry related field 𝔄. It is sparsely covered by locations of symmetry centers. The central governance operator ℊ administers these locations. The symmetry centers contain symmetry related charges. The locations of these charges are influenced by the symmetry related field 𝔄.
8. Field Dynamics
In the model that we selected, the dynamics of the fields are described by quaternionic differential calculus. Apart from the eigenspaces of reference operators and the symmetry centers we encountered two fields that are defined by quaternionic functions and corresponding operators. One is the symmetry related field 𝔄 and the other is the embedding field ℭ.
determines the dynamics of the symmetry centers. ℭ gets deformed and vibrated by the recurrent embedding of point-like elementary particles that each reside on an individual symmetry center.
Apart from the way that they are affected by point-like artifacts that disrupt the continuity of the field, both fields obey, under not too violent conditions and over not too large ranges, the same differential calculus.
Under rather general conditions the change of a quaternionic function 

Here the coefficients 


Under more moderate and sufficiently short range conditions the function behaves more linearly.

Here the coefficients 
Thus, in a rather flat continuum we can use the quaternionic nabla




In this form the differential equations can still describe point-like disruptions of the continuity of the field.
Double differentiation will then result in the quaternionic wave equation:

Here 


Function 

The wave equation can be split into two continuity equations:


If 



8.1. Fourier Equivalents
In this quaternionic differential calculus, differentiation is implemented as multiplication.
This is revealed by the Fourier equivalents of the Equations (4) through (10) in the previous paragraph:

The nabla 




The equivalent of the quaternionic wave equation is:

The continuity equations result in:


8.2. Poisson Equations
The Poisson equation is a special condition of the non-homogeneous wave equation in which some terms are zero or have a special value.



The 3D solution of this equation is determined by the screened Green’s function
Green functions represent solutions for point sources.


G(r) has the shape of the Yukawa potential [9]
In case of 
8.3. Solutions of the Homogeneous Wave Equation
Solutions of the homogeneous wave equations are of special interest because for odd numbers of participating dimensions this equation has solutions in the form of wave-fronts.
The homogeneous wave equation is given by:


Equation (2) has three-dimensional spherical wave fronts as one group of its solutions. 

where 




Here 
Equation (4) has one-dimensional wave fronts as one group of its solutions:

Again the parameter 

The imaginary 

That orientation determines the polarization of the one-dimensional wave front.
9. Regeneration and Detection
The regeneration of an elementary particle by the controlling mechanism involves the creation of a new embedding location. Detection stops this regeneration process. At detection, the set 

After regeneration of the complete set






10. Photons
Photons are configured by solutions of the wave equation. For odd numbers of participating dimensions the solutions of the homogeneous wave equation are combinations of wave fronts. In three dimensions the spherical wave fronts diminish their amplitude as 1/r with distance r of the trigger point. One-dimensional wave fronts keep their amplitude. As a consequence these wave fronts can travel huge distances through the field that supports them. Each wave front can carry a bit of information and/or energy. In order to reach these distances the carrying field must exist long enough and it must reach far enough.
The symmetry related field 𝔄 does not fulfil the requirements for long distance travel. It depends on the nearby existence of symmetry related charges and its amplitude also diminishes as 1/r with distance from the charge.
The embedding field ℭ is a better candidate for long distance transfer of energy and information. ℭ exists always and everywhere. One-dimensional wave fronts vibrate the ℭ field, but do not deform this field. They just follow existing deformations.
Creating a string of one-dimensional wave fronts requires a recurrent wave front generation process. Such processes do not underlay the generation of symmetry related charges that support the 𝔄 field. However, such processes exist during the recurrent embedding of artifacts that occurs in the ℭ field.
Recurrent generation of spherical wave fronts is capable to deform the corresponding field. It has similar effects as a stationary deformation by a point-like artifact has.
The fixed speed of wave fronts translates in the same fixed speed for the photons. A string of one-dimensional wave fronts can carry a quantized amount of energy. The relation 
However, observations of long range effects over cosmological distances reveal that these relations do not hold over huge distances. Red-shift of patterns of “old” photons that are emitted by atoms and arrive from distant galaxies indicate that the spatial part of field ℭ is extending as a function of progression.
With the interpretation of photons as strings of wave fronts this means that the duration of emission and the duration of absorption are also functions of progression. As a consequence, some of the emitted wave fronts are “missed” at later absorption. The detected photon corresponds to a lower energy and a lower frequency than the emitted photon has. According to relation 
Thus, the wave equation may be valid in the vicinity of the images of symmetry centers inside ℭ, but does not properly describe the long range behavior of ℭ. Due to its restricted range and the non-recurrent generation of its charges, the 𝔄 field does not show the equivalents of photons and red-shift phenomena.
The long range phenomena of photons indicate that the parameter space ℜ⓪ of ℭ may actually own an origin. For higher progression values and for most of the spatial reach of field ℭ, that origin is located at huge distances. Information coming from low progression values arrives with photons that have travelled huge distances. They report about a situation in which symmetry centers were located on average at much smaller inter-distances.
11. Conclusions
By introducing a background space and a set of symmetry center types, this paper exploits the way in which quaternionic number systems can be ordered. This distinguishes between Cartesian ordering and spherical ordering and it reveals that these ordered versions of the number systems exist in several distinct symmetry flavors. Locally, the background space needs no origin and as a consequence it does not feature spin. The coupling of symmetry centers onto the background space offers the possibility to define an algorithm that computes corresponding symmetry related charges that are in agreement with the short list of electric charges and other discrete properties of elementary particles. For example, also the diversity of color charge and spin can be explained in this way. This indicates that elementary particles inherit these properties from the space in which they reside.
An important role is played by controlling mechanisms that are not part of the Hilbert spaces, but that make use of the Hilbert spaces as a structured storage medium. The elementary particles inherit their properties both from the Hilbert space and from these controlling mechanisms.
This paper considers the embedding field ℭ because it uses the same parameter space ℜ as the symmetry related field 𝔄 does. The embedding field obeys the same quaternionic differential calculus as the symmetry related field, but the triggers that cause discontinuities differ fundamentally among these fields. That is why these fields behave differently. Still both fields determine the kinematics of elementary particles. This is treated in more detail in [8] .
The section about photons indicates that in contrast to what is usually suggested photons are not waves of the electric field 𝔄. Instead they vibrate the embedding field ℭ and follow its deformations. They do not deform this field themselves.
The behavior of “old” photons indicates that the validity range of the wave equation is restricted.
Cite this paper
Johannes Antonie Josephus van Leunen, (2015) On the Origin of Electric Charge. Open Access Library Journal,02,1-14. doi: 10.4236/oalib.1101836
References
- 1. In 1843 quaternions were discovered by Rowan Hamilton.
http://en.wikipedia.org/wiki/History_of_quaternions - 2. Quantum logic was introduced by Garret Birkhoff and John von Neumann in their paper: Birkhoff, G. and von Neumann, J. (1936) The Logic of Quantum Mechanics. Annals of Mathematics, 37, 823-843.
This paper also indicates the relation between this orthomodular lattice and separable Hilbert spaces. - 3. The Hilbert space was discovered in the first decades of the 20th century by David Hilbert and others.
http://en.wikipedia.org/wiki/Hilbert_space. - 4. In the sixties Israel Gelfand and GeorgyiShilov introduced a way to model continuums via an extension of the separable Hilbert space into a so called Gelfand triple. The Gelfand triple often gets the name rigged Hilbert space. It is a non-separable Hilbert space.
http://www.encyclopediaofmath.org/index.php?title=Rigged_Hilbert_space - 5. Paul Dirac introduced the braket notation, which popularized the usage of Hilbert spaces. Dirac also introduced its delta function, which is a generalized function. Spaces of generalized functions offered continuums before the Gelfand triple arrived.
See: Dirac, P.A.M. (1958) The Principles of Quantum Mechanics. 4th Edition, Oxford University Press, Oxford, ISBN 978 0 19 852011 5. - 6. Quaternionic function theory and quaternionic Hilbert spaces are treated in: van Leunen, J.A.J. (2015) Quaternions and Hilbert Spaces.
http://vixra.org/abs/1411.0178 . - 7. In the second half of the twentieth century Constantin Piron and Maria Pia Solèr proved that the number systems that a separable Hilbert space can use must be division rings. See: Baez, J. (2011) Division Algebras and Quantum Theory.
http://arxiv.org/abs/1101.5690 and Holland, S.S. (1995) Orthomodularity in Infinite Dimensions: A Theorem of M. Solèr. Bulletin of the American Mathematical Society, 32, 205-234
http://www.ams.org/journals/bull/1995-32-02/S0273-0979-1995-00593-8/ - 8. van Leunen, J.A.J. (2015) Foundation of a Mathematical Model of Physical Reality.
http://vixra.org/abs/1502.0186 - 9. http://en.wikipedia.org/wiki/Yukawa_potential




