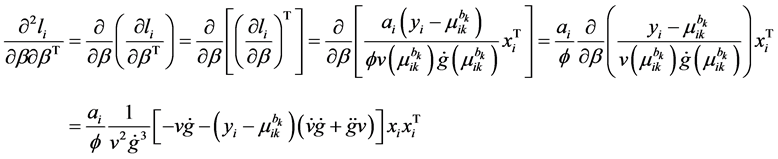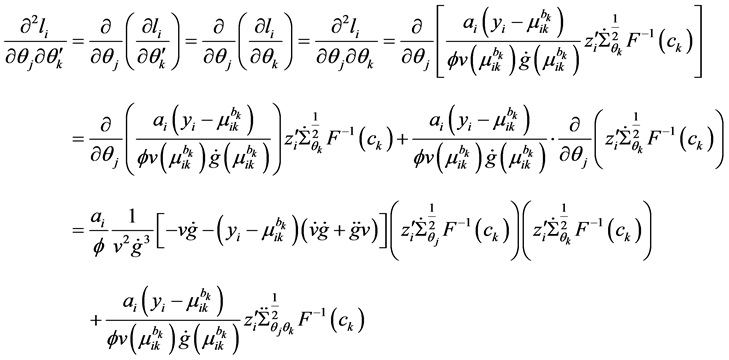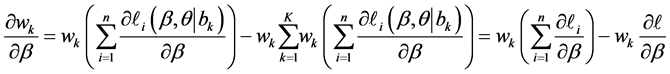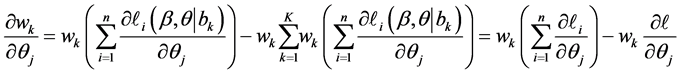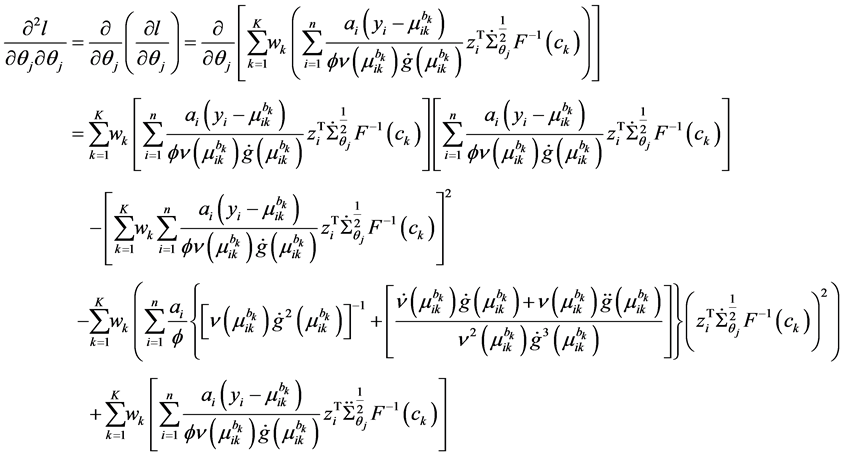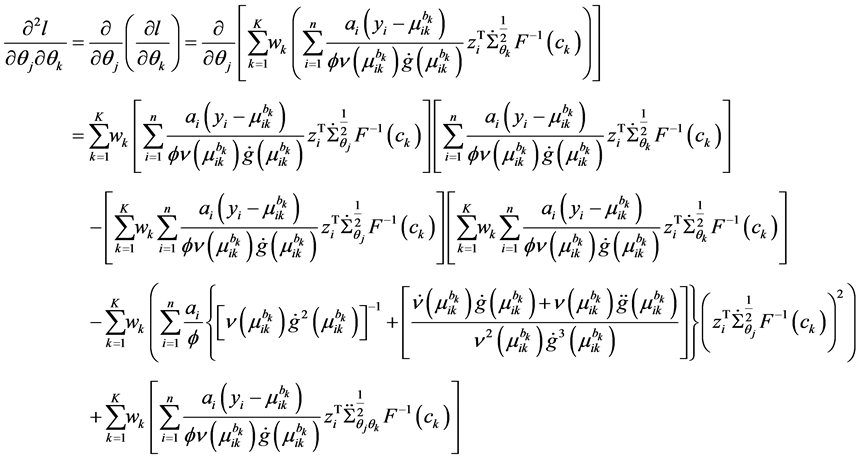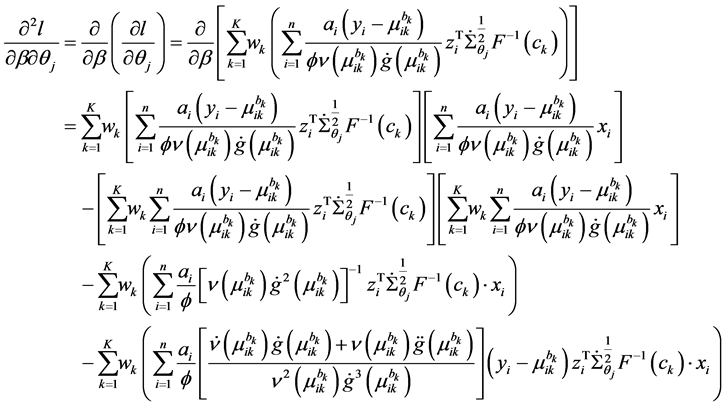Open Access Library Journal
Vol.02 No.10(2015), Article ID:68658,16 pages
10.4236/oalib.1102002
Quasi-Monte Carlo Estimation in Generalized Linear Mixed Model with Correlated Random Effects
Yin Chen1, Yu Fei2, Jianxin Pan3*
1School of Insurance, University of International Business and Economics, Beijing, China
2School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming, China
3School of Mathematics, University of Manchester, Manchester, UK
Email: chenyin@uibe.edu.cn, feiyukm@aliyun.com, *jianxin.pan@manchester.ac.uk
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 August 2015; accepted 28 September 2015; published 12 October 2015

ABSTRACT
Parameter estimation by maximizing the marginal likelihood function in generalized linear mixed models (GLMMs) is highly challenging because it may involve analytically intractable high-dimen- sional integrals. In this paper, we propose to use Quasi-Monte Carlo (QMC) approximation through implementing Newton-Raphson algorithm to address the estimation issue in GLMMs. The random effects release to be correlated and joint mean-covariance modelling is considered. We demonstrate the usefulness of the proposed QMC-based method in approximating high-dimensional integrals and estimating the parameters in GLMMs through simulation studies. For illustration, the proposed method is used to analyze the infamous salamander mating binary data, of which the marginalized likelihood involves six 20-dimensional integrals that are analytically intractable, showing that it works well in practices.
Keywords:
Generalized Linear Mixed Models, Correlated Random Effects, Quasi-Monte Carlo, Mean-Covariance Modelling, High-Dimensional Integrals, Newton-Raphson Method
Subject Areas: Mathematical Statistics

1. Introduction
McCullagh and Nelder (1989) [1] analyzed a challenging salamander mating binary data set which was conducted on two geographically isolated populations, Roughbutt (RB) and Whiteside (WS), in three experiments (one in summer 1986 and two in fall 1986). The question of interest is to determine whether or not certain barriers to interbreeding have evolved over time in geographically isolated populations. The second question is to determine whether or not heterogeneity between individuals (females and males) exists. The RB and WS populations are ideal for these experiments because salamanders would never meet those from different population in their natural environment, so that there are two closed groups in each experiment. Each group involved five females and five males from each population. Each female mated with six males, three from each population. So each closed group resulted in sixty correlated binary observations (1 for successful mating; 0 for failed mating). Therefore, the binary data set is crossed, balanced (as each female mated with a total of six males and vice verse) and incomplete (as each female mated with just three out of a possible five males, and vice verse). The data can be analyzed by using a specific generalized linear mixed model.
Generalized linear mixed models (GLMMs) are very useful for non-Gaussian correlated or clustered data and widely applied in many areas including epidemiology, ecological, and clinical trials. Parameters estimation in GLMMs is, however, very challenging, and correlated binary data is even more difficult to analyze than continuous data. This is because the marginalized likelihood function, obtained by integrating out multivariate random effects from the joint density function of the responses and random effects, is in general analytically intractable. For example, the likelihood function for the pooled salamander mating data described above involves six 20-dimensional integrals which are analytically intractable. In the literature, the marginalized likelihood function was considered by two typical methods: a) analytical Laplace approximation to integrals: This is represented by the work of Breslow and Clayton (1993) [2] who developed the penalized quasi-likelihood (PQL) estimation. Unfortunately, approaches based on Laplace approximation may yield biased estimates of variance components, particularly for modeling correlated binary data. This difficulty has stimulated a number of alternative approaches. For example, Lin and Breslow (1996) [3] proposed a corrected penalized quasi-likelihood, and Lee and Nelder (2001) [4] developed hierarchical generalized linear models (HGLMs) procedure; b) numerical techniques to approximate the likelihood function and estimate the parameters: Karim and Zeger (1992) [5] developed a Bayesian approach with Gibbs sampling for GLMMs, but its computational efforts may be computationally intensive. Monte Carlo Expectation-Maximization (MCEM) and Monte Carlo Newton-Raphson (MCNR) algorithms were proposed to approximate the maximum likelihood estimates in GLMMs by McCulloch (1994, 1997) [6] [7] . However, iterations of MCEM and MCNR do not always converge to the global maximum and are also very computationally intensives for high-dimensional problems (Chan, Kuk and Yam, 2005) [8] . Pan and Thompson (2003, 2007) [9] [10] developed Gauss-Hermite Quadrature (GHQ) approach and Quasi-Monte Carlo (QMC) approximation. Aleid and Pan (2008) [11] used Randomized Quasi-Monte Carlo (RQMC) to solve the integration problem in GLMMs. It is noted that most of the work above assume that random effects in GLMMs, which characterize the heterogeneity among individuals, are mutually independent and normally distributed.
However, these assumptions may not always hold due to the likely correlation of random effects, for instance. At least, the independence assumption of random effects should be testable. Misspecification of random effects covariance structure may yield inefficient estimates of parameters and can cause the problem of biased estimates of variance components, making statistical inferences for GLMMs unreliable. In this paper, we release the assumption of independence for random effects and aim to develop a new methodology which can model the covariance structures of random effects in GLMMs. Covariance modeling strategy based on a modified Cholesky decomposition is studied within the framework of GLMMs. The paper is organized as follows. GLMMs and the marginalized Quasi-likelihood are briefly reviewed in Section 2. The QMC approximation, the simplest good point set and analytical form of the MLEs for GLMMs are discussed in Section 3. Covariance modeling strategy through a modified Cholesky decomposition is described in Section 4. In Section 5, the salamander data set is analyzed as an example for illustration of the use of the new method. Simulation studies with the same design protocol as the salamander data are conducted in Section 6. Discussions on the related issues and further studies are presented in Section 7.
2. Generalized Linear Mixed Models
Let 
 denote the observed responses. Assume that
denote the observed responses. Assume that 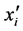 is the
is the  row of design matrix X;
row of design matrix X; 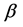 is the
is the 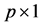 fixed effects parameter;
fixed effects parameter; 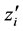 is the
is the  row of the second design matrix Z; and b is the
row of the second design matrix Z; and b is the 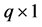 random effects.
random effects.
The GLMMs are of the form
 , (1)
, (1)
where  is a monotonic and differentiable link function. Given random effects b, the responses
is a monotonic and differentiable link function. Given random effects b, the responses 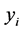 are independent and follow an exponential family of distributions with the density
are independent and follow an exponential family of distributions with the density
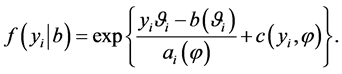 (2)
(2)
The conditional mean and variances, given random effects b, are given by  and
and
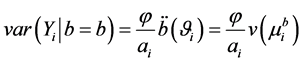 , respectively, where
, respectively, where  is a prior weight,
is a prior weight,  is an overdispersion scalar,
is an overdispersion scalar,

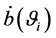


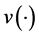
When the linear predictor 
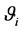
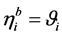

Note q-dimensional random effects b are assumed to be normally distributed with mean 0 and positive definite variance-covariance matrix
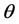
Quasi-likelihood function of the fixed effects 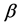

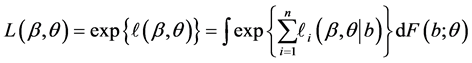
where
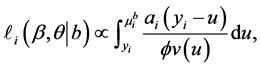
so that
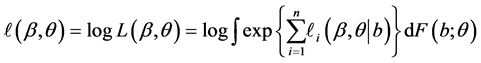
is the conditional log quasi-likelihood of 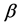
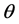
It is challenging to calculate the maximum likelihood estimates (MLEs), 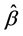
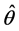
3. Quasi-Monte Carlo Integration and Estimation
3.1. Monte Carlo (MC) Integration
In this section, Quasi-Monte Carlo (QMC) approach is used to approximate high dimensional integrals. The traditional Monte Carlo (MC) method is outlined first as follow. Let 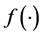


Assume K independent random samples 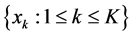

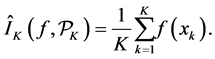
According to the strong law of large number, the approximation 

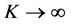

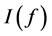



Since the rate of convergence is independent of q, the MC approximation seems to be very appealing. However, the MC algorithm has some serious drawbacks (see, e.g., Niederreiter, 1992 [12] ; Spanier and Maize, 1994 [13] ). One of these deficiencies is that even though the rate of convergence is independent of the dimension, the convergence is very slow. On the other hand, it may suffer from the problem of generating genuinely random samples. Instead, pseudo-random samples are generated and used to approximate the integral (Traub and Wozniakowski, 1992 [14] ). It is also noted that the MC method only provides probabilistic error bounds, which is not a desirable as it does not guarantee reliable estimation results. As an alternative to the MC methods, Quasi- Monte Carlo approximation method is considered.
3.2. Quasi-Monte Carlo Method and Lattice Rule
Quasi-Monte Carlo (QMC) sequences are a deterministic alternative to Monte Carlo sequences (Niderreiter, 1992). In contrast to MC sequences, QMC sequences have a property that they are uniformly distributed on the unit cube. Thus, QMC approximation has the same equation as (8) but the MC random samples are replaced by deterministic samples that are uniformly distributed on the domain. Uniformity of sequences is measured by means of discrepancy, and for this reason QMC sequences are also called low-discrepancy sequences. Note the Koksma-Hlawka inequality
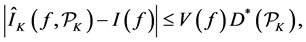
where 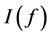
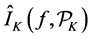
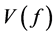
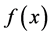

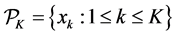

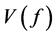
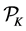
that the absolute integration error has an order

chosen such that their start discrepancy is close to

In the QMC approach, there are many good algorithms for generating such integration nodes. One set of such integration nodes is called good point set and discussed below.
3.3. Good Point (GP) Set
Denote a good point by 

percube. The set 



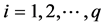
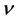
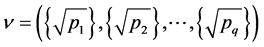
where 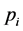

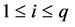
3.4. MLE via QMC Approximation
Suppose 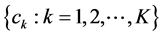

where 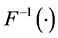
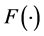

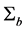
example, it can be taken as the Cholesky decomposition of 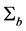
Let


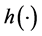
the inverse function of the link function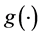
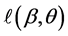
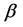

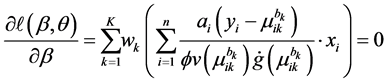

where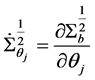
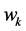
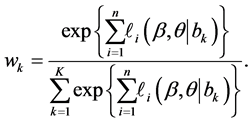
Note that the weight 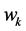



In general, the score equations in (12)-(13) have no analytical solutions for 
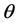
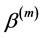
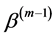
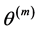

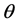
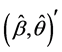
4. Modeling of Covariance Structures of Random Effects
Misspecification of covariance structures of random effects may cause problems of inefficient estimates of parameters in GLMMs. In some circumstances, it may lead to biased estimates of the parameters. Hence, in this paper we propose to model the covariance structure of random effects in GLMMs, rather than specify a structure to the covariance matrix 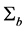
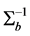
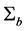
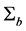
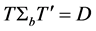
where
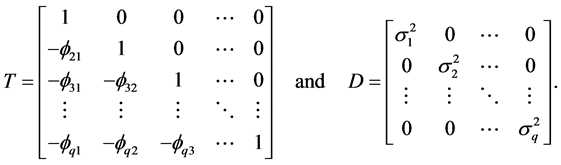
Thus, 
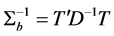
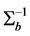
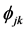
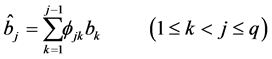
where 
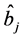

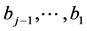
novation variances (IVs), i.e., 

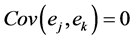

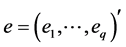


In a spirit of Pourahmadi (1999) [17] , we propose to model the ACs and the logarithm of the IVs using linear regression models
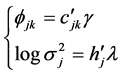
where 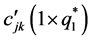
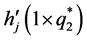
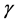
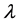
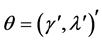
5. Salamander Data Analysis
Assume that 
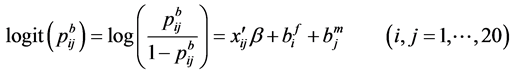
where 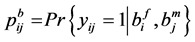
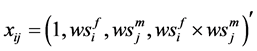



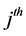
Note that each experiment involves 40 salamanders so that the log-likelihood function for each experiment involves one 40-dimensional integral. It can be further reduced to the sum of two 20-dimensional integrals due to the block design of the two closed groups, see Karim and Zeger (1992) [5] and Shun (1997) [23] for more details about the design. When the three-experiment data sets are pooled as those in model (19), the log-likelihood function 


We now apply the proposed covariance modeling method to the salamander mating data. Note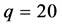

where 



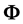
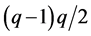
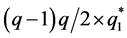
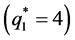
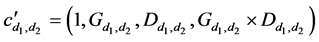
where 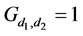


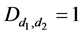
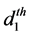
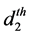
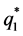
The model for the innovation variances is
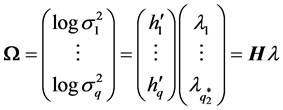
where 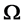
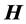
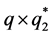


where 
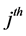
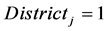

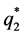
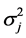

The pooled data are now analyzed using the proposed QMC approach. The MLEs of the fixed effects and variance components in the model are calculated. Specifically, we implement the simplest QMC points, square root sequences, to approximate the 20-dimensional analytically intractable integrals. A set of 20-dimensional points on the unit cube 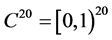

Note that the covariance modeling for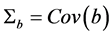
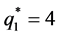

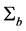
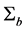
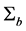
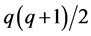


We code our programme in FORTRAN and run on a PC Pentium (R) 4 PC (CPU 3.20 GHz). We choose the PQL estimate as the starting value of
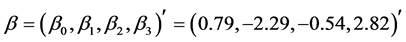
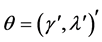
Table 1. MLEs of the parameters via covariance modelling for the pooled salamander mating data using square root sequences by varying K, the number of square root sequence points (standard errors in parentheses).
log-likelihood 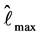


It is noted that in the autoregressive coefficients model, the estimates of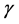

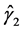

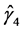


In other words, T is an identity matrix and D is a diagonal matrix with an identical element on diagonals, implying 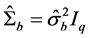
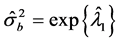
By comparing the numerical results of the QMC estimation approach with the literature work, we find that they are quite close to those made by Gibbs sampling method. But the QMC method has much light computational loads and easy to use for practitioners. This is because Gibbs sampling method involves multiple draws of random samples and needs more experience, for instance, in specifying prior distributions of parameters, etc., whereas the QMC approximation method does not need such specifications. Also, Gibbs sampling may be very slow in obtaining the parameter estimates. On the other hand, the PQL approach gives very biased estimates of the variance components for modeling clustered binary data, as reported by many authors including Breslow and Clayton (1993) [2] , Breslow and Lin (1995) [24] , Booth and Hobert (1999) [25] and Aiken (1999) [26] .
6. Simulation
In this section, we carry out simulation studies to assess the performance of the proposed QMC estimation method in GLMMs. In the simulation studies we consider the logistic model (19) and use the same protocol of design as the real salamander mating experiment, resulting in 360 correlated binary observations. We run 100 simulations and calculate the average of the parameter estimates over the 100 simulations. The log-likelihood function for each simulated data set involves six 20-dimensional integrals that are analytically intractable.
We generate 

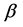
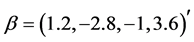
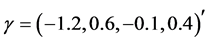
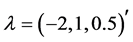
From Table 2 it is clear that the proposed QMC approach is able to produce reasonably good estimates of parameters in GLMMs even if there are heterogenous random effects. The estimates of the fixed effects and variance components, based on the average of 100 simulation results, are quite close to the true values of the parameters. It implies that the proposed QMC approach with covariance modeling strategy works well in estimating parameters in GLMMs with correlated random effects.
7. Discussions
We have studied the performance of using QMC approach to calculate the MLEs of the fixed effects and variance components in GLMMs with correlated random effects. We proposed to use Newton-Raphson algorithm to calculate the parameter estimates. The marginalized log-likelihood function that is in general analytically intractable is approximated well through the use of the simplest QMC points, i.e., square root sequences. We also addressed the issue of covariance modelling for random effects covariance matrix through a modified Cholesky decomposition. As a result, pre-specification of covariance structures for random effects is not necessary and misspecification of covariance structures is thus avoided. The score function and observed information matrix are calculated and expressed in analytically closed forms, so that the algorithm can be implemented straightforwardly. The performance of the proposed method was assessed through real salamander mating data analysis and simulation studies. Even though the marginalized log-likelihood function in the numerical analysis involves six 20-dimensional analytically intractable integrals, the QMC square root sequence approximation performs very well.
Table 2. Average of 100 parameter estimates in the simulation studies, where the QMC approximation uses 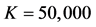
In general, a practical issue for the use of the QMC points is the choice of the number of integration nodes. Pan and Thompson (2007) [10] suggested to increase the number of integration points gradually until the estimation results become relatively stable. This is exactly what we have done in the numerical analysis displayed in Table 1.
Acknowledgements
We thank the editors and the reviewers for their comments. This research is funded by the National Social Science Foundation No.12CGL077, National Science Foundation granted No.71201029, No.71303045 and No.11561071. This support is greatly appreciated.
Cite this paper
Yin Chen,Yu Fei,Jianxin Pan, (2015) Quasi-Monte Carlo Estimation in Generalized Linear Mixed Model with Correlated Random Effects. Open Access Library Journal,02,1-16. doi: 10.4236/oalib.1102002
References
- 1. McCulloch, P. and Nelder, J.A. (1989) Generalized Linear Models. 2nd Edition, Chapman and Hall, London.
http://dx.doi.org/10.1007/978-1-4899-3242-6 - 2. Breslow, N.E. and Clayton, D.G. (1993) Approximate Inference Ingeneralized Linear Mixed Models. Journal of the American Statistical Association, 88, 9-25.
- 3. Lin, X. and Breslow, N.E. (1996) Bias Correction in Generalized Lnear Mixed Models with Multiple Components of Dispersion. Journal of the American Statistical Association, 91, 1007-1016.
http://dx.doi.org/10.1080/01621459.1996.10476971 - 4. Lee, Y. and Nelder, J.A. (2001) Hierrarchical Generalized Linear Models: A Synthesis of Generalized Linear Models, Random Effect Models and Structured Dispersions. Biometrika, 88, 987-1006.
http://dx.doi.org/10.1093/biomet/88.4.987 - 5. Karim, M.R. and Zeger, S.L. (1992) Generalized Linear Models with Random Effects; Salamnder Mating Revisited. Biometrics, 48, 681-694.
http://dx.doi.org/10.2307/2532317 - 6. McCulloch, C.E. (1994) Maximum Likelihood Variance Components Estimation for Binary Data. Journal of the American Statistical Association, 89, 330-335.
http://dx.doi.org/10.1080/01621459.1994.10476474 - 7. McCulloch, C.E. (1997) Maximum Likelihood Algorithms for Generallized Linear Mixed Models. Journal of the American Statistical Association, 92, 162-170.
http://dx.doi.org/10.1080/01621459.1997.10473613 - 8. Chan, J.S., Kuk, A.Y. and Yam, C.H. (2005) Monte Carlo Approximation through Gibbs Output in Generalized Linear Mixed Models. Journal of Maltivariate Analysis, 94, 300-312.
http://dx.doi.org/10.1016/j.jmva.2004.05.004 - 9. Pan, J. and Thompson, R. (2003) Gauss-Hermite Quadrature Approximation for Estimation in Generalised Linear Mixed Models. Computational Statistics, 18, 57-78.
- 10. Pan, J. and Thompson, R. (2007) Quasi-Monte Carlo Estimation in Generalized Linear Mixed Models. Computational Statistics and Data Analysis, 51, 5765-5775.
http://dx.doi.org/10.1016/j.csda.2006.10.003 - 11. Ye, H. and Pan, J. (2006) Modelling Covariance Structures in Generalized Estimating Equations for Longitudinal Data. Biometrika, 93, 927-941.
http://dx.doi.org/10.1093/biomet/93.4.927 - 12. Niederreiter, H. (1992) Random Number Generation and Quasi-Monte Carlo Methods. SIAM, Philadelphia.
http://dx.doi.org/10.1137/1.9781611970081 - 13. Spanier, J. and Maize, E. (1994) Quasi-Random Methods for Estimating Integrals Using Relatively Small Samples. SIAM Review, 36, 19-44.
http://dx.doi.org/10.1137/1036002 - 14. Traub, J.F. and Wozniakowski, H. (1992) The Monte Carlo Algorithm with Pseudorandom Generator. Mathematics of Computation, 58, 323-339.
http://dx.doi.org/10.1090/S0025-5718-1992-1106984-4 - 15. Fang, K.T. and Wang, Y. (1994) Number-Theoretic Methods in Statistics. Chapman and Hall, London.
http://dx.doi.org/10.1007/978-1-4899-3095-8 - 16. Morokoff, W.J. and Caflisch, R.E. (1995) Quasi-Monte Carlo Integration. Journal of Computational Physics, 122, 218-230.
http://dx.doi.org/10.1006/jcph.1995.1209 - 17. Pourahmadi, M. (1999) Joint Mean-Covariance Models with Applications to Longitudinal Data: Unconstrained Parameterization. Biometrika, 86, 677-690.
http://dx.doi.org/10.1093/biomet/86.3.677 - 18. Pourahmadi, M. (2000) Maximum Likelihood Estimation of Generalised Linear Models for Multivariate Normal Covariance Matrix. Biometrika, 87, 425-435.
http://dx.doi.org/10.1093/biomet/87.2.425 - 19. Daniels, M.J. and Pourahmadi, M. (2002) Bayesian Analysis of Covariance Matrices and Dynamic Models for Longitudinal Data. Biometrika, 89, 553-566.
http://dx.doi.org/10.1093/biomet/89.3.553 - 20. Daniels, M.J. and Zhao, Y.D. (2003) Modelling the Random Effects Covariance Matrix in Longitudinal Data. Statistics in Medicine, 22, 1631-1647.
http://dx.doi.org/10.1002/sim.1470 - 21. Smith, M. and Kohn, R. (2002) Parsimonious Covariance Matrix Estimation for Longitudinal Data. Journal of the American Statistical Association, 97, 1141-1153.
http://dx.doi.org/10.1198/016214502388618942 - 22. Pan, J. and MacKenzie, G. (2003) On Modelling Mean-Covariance Structures in Longitudinal Studies. Biometrika, 90, 239-244.
http://dx.doi.org/10.1093/biomet/90.1.239 - 23. Shun, Z. (1997) Another Look at the Salamander Mating Data: A Modified Laplace Approximation Approach. Journal of the American Statistical Association, 92, 341-349.
http://dx.doi.org/10.1080/01621459.1997.10473632 - 24. Breslow, N.E. and Lin, X. (1995) Bias Correction in Generalised Linear Mixed Models with a Single-Component of Dispersion. Biometrika, 82, 81-91.
http://dx.doi.org/10.1093/biomet/82.1.81 - 25. Booth, J.G. and Hobert, J.P. (1999) Maximizing Generalized Linear Mixed Model Likelihoods with an Automated Monte Carlo EM Algorithm. Journal of the Royal Statistical Society, B, 61, 265-285.
http://dx.doi.org/10.1111/1467-9868.00176 - 26. Aitken, M. (1999) A General Maximum Likelihood Analysis of Variance Components in Generalized Linear Models. Biometrics, 55, 117-128.
http://dx.doi.org/10.1111/j.0006-341X.1999.00117.x
Appendix A: Second-Order Derivatives of Log-Likelihood
The second-order derivatives of log-likelihood function is given by
Appendix B: MLEs for Covariance Modeling
The first and second derivative of 


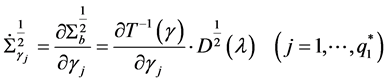


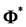


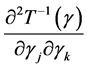
trix 

Every element in 
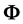
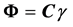

We can put the jth column of C into a 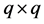


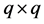
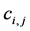


have the relationship 
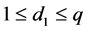
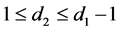

The above relationship is a one-to-one correspondence between i and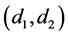

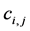
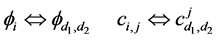
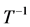


are all lower triangular matrices. Denote 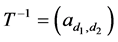
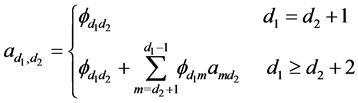
The first derivative can be calculated as
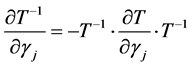
where 

The second derivative can be calculated as
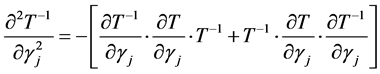

because of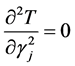

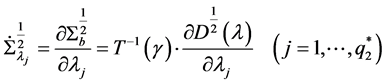
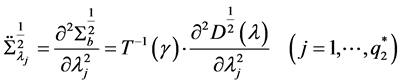
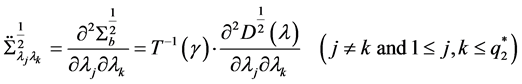
where
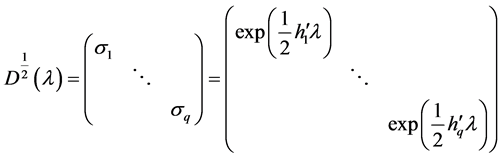

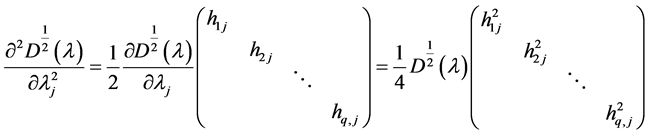
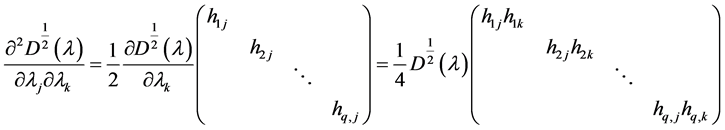
NOTES
*Corresponding author.